This document summarizes a doctoral dissertation on geometric and viscosity solutions to first order Cauchy problems. It introduces two types of solutions - viscosity solutions and minimax solutions - which are generally different. The aim is to show that iterating the minimax procedure over shorter time intervals approaches the viscosity solution. This extends previous work relating geometric and viscosity solutions in the symplectic case. The document outlines characteristics methods, generating families, Clarke calculus tools, and a proof constructing generating families to relate iterated minimax solutions to viscosity solutions.

1. Geometric and viscosity solutions for the
Cauchy problem of first order
Juliho Castillo, M.Sc.
Instituto de Matem´aticas, UNAM
Doctoral Examination: August 30, 2017

2. Abstract
There are two kinds of solutions of the Cauchy problem
of first order, the viscosity solution and the more
geometric minimax solution and in general they are
different. The aim of this dissertation is to show how
they are related: iterating the minimax procedure during
shorter and shorter time intervals one approaches the
viscosity solution.This can be considered as an extension
to the contact framework of the result of Q. Wei [Wei]
in the symplectic case.

3. Section 1
Introduction

4. Consider the Cauchy problem



∂tu(t, x) + H(t, x, ∂xu(t, x), u(t, x)) = 0, t ∈ (0, T]
u(0, t) = v(x), x ∈ Rk
.
(C.P.F.O.)

5. The classical method to solve this problem, for v ∈ C2
and a
short time interval, consists in solving characteristics equations
˙x = ∂yH
˙y = −∂xH − y∂zH
˙z = y∂yH − H,
(Eq. Char.)
to get the characteristic lines
Φ(t, q0) ˙=(t, x(t, q0), y(t, q0), z(t, q0));
(where Φ(0, q0) = (0, q0)) and then obtain the solution u(t, x)
of the Cauchy problem as follows: setting ut(x) ˙=u(t, x), for
fixed t, and its 1-jet j1
ut(x) = (x, dut(x), ut(x)), the image of
j1
ut is the section at time t of the union
L (Λ0) =
t∈[0,T]
Φ(t, Λ0) = {Φ(t)| t ∈ [0, T], Φ(0) ∈ Λ}

6. of the characteristic lines
Φ(t, Λ0) = {Φ(t)| Φ(0) ∈ Λ0} , t ∈ [0, T]
passing through Λ0 = {(0, j1
v(x)}.

7. This procedure does not yield a global solution of the problem
in the whole interval [0, T], as the geometric solution L it is
not always the set {(t, j1
ut(x))} for a function u(t, x).

8. According to [Arnold, section 3.2] the wavefront
F = π (L(Λ0)) ,
(where π (t, x, y, z) = (t, x, z)) obtained in (t, x, y, z) space by
solving the equation
dz = −H(t, x, y, z)dt + ydx
restricted to (t, x, y, z) ∈ L it is not the graph of a function:
the projected characteristics
π (Φ(t, q0)) = (t, x(t, q0), z(t, q0)), q0 ∈ Λ0
may cross after some time. For example, characteristics for
conservation laws [Evans, example 3.2.5]

10. Whereas in some applications, e.g. to geometrical optics, the
wavefront F can be considered as a solution of the physical
problem, one is interested in a single-valued solution u(t, x).
Assuming that the projection of F into (t, x) space is onto,
one can construct such a solution as a section of the
wavefront, selecting a single u over each (t, x). When the
function H is sufficiently convex with respect to y (and v is
not too wild at infinity), such a “selector” consists in choosing
for u(t, x) the smallest u with (t, x, u) ∈ F.

11. This min solution happens to be the “viscosity solution” which
was first introduced as the viscosity limit when ε → 0+
of the
solution of the Cauchy problem for the viscous equation
∂tu(t, x) + H(t, x, ∂xu, u) = ε xu(t, x),
and afterwards got a general definition for general nonlinear
first order partial differential equations in the work of Crandall,
Evans and Lions [CEL] [CEL, BCD].

12. In the non-convex case the viscosity solution may not be a
section of the wavefront (see for example [Checiner]). On the
other hand, Chaperon introduced in [Chaperon] weak
solutions whose graph is a section of the wavefront, obtained
by a “minimax” procedure which generalizes the minimum
considered in the convex case and relies on the existence of
suitable generating families for the geometric solution.

13. Let’s explain in more detail the procdeure: At first, considere
the legendrian submanifold Λ = ϕt
(j1
v) ⊂ J1
Rk
, for some
Rk
, where ϕt
is the flow generated by (Eq. Char.) and
therefore Φ(t) = (t, ϕ(t)) .

14. It turns out that there exist a so called generating function
quadratic at infinity
SH,v : [0, T] × Rk
× Rq
, (t, x, ξ) → St
H,v(x, ξ)
(for some Rq
, a family of parameters ξ) such that
Λ = x, ∂xSt
H,v(x, ξ), St
H,v(x, ξ) ∂ξSt
H,v(x, ξ) = 0 .

15. Now we can define a minimax selector such that
u(t, x) = infmaxξ St
H,v(x, ξ)
is a generalized solution of Cauchy problem (C.P.F.O.). It is
called the minimax solution. But in general this is not a
classical solution. Indeed ut ∈ CLip
Rk
.

16. Although, we have been considering v ∈ C2
(Rk
), in the more
general setting of Clarke calculus, we can consider
v ∈ C2
(Rk
), and thus for a given H ∈ C2
(J1
Rk
), we obtain
an operator
RH : CLip
(Rk
H) → CLip
(Rk
), v → infmaxξ St
H,v(·, ξ).

17. One may to try to get a solution as a limit obtained by
dividing a given time interval into small pieces and iterating
the minimax procedure step by step.

18. Our goal is to show that when the size of the time intervals go
to zero, one indeed gets the viscosity solution as the limit
Theorem 1.
Suppose H ∈ C2
c ([0, T] × J1
(Rk
)), v ∈ CLip
(Rk
). Then the
viscosity solution is the limit of iterated minimax solutions for
problem (C.P.F.O.) on [0, T].

19. This extends the result obtained by Q. Wei [Wei] in the
symplectic framework.

20. Section 2
Cauchy Problem

21. Characteristics method
For a given function H ∈ C2
[0, T] × J1
Rk
, the following
statement relates solutions u : [0, T] × Rk
→ R for Cauchy
problem of First Order (C.P.F.O.) (being u0 : Rk
→ R the
initial condition) and solutions for characterics equations
(Eq. Char.) starting at the 1−graph of S0 :

22. Characteristics method
Suppose that u ∈ C2
([0, T] × Rk
) is a solution for the given
Cauchy problem (C.P.F.O.). Then, if a solution for the
equation
˙x = ∂yH (t, x, ∂xu, u) , (2.1)
on [0, T] is given, the curve defined by
(x(t), y(t), z(t)) = (x(t), ∂xu(t, x(t)), u(t, x(t))) . (2.2)
is a solution for characteric equations (Eq. Char.).

23. Characteristics method
Conversely, u0 ∈ C1
(M), T is small enough and
(X(t,x), Y(t,x), Z(t,x)) : [0, T] → J1
Rk
is the unique solution for characteristic characteristics
(Eq. Char.) with boundary conditions



X(t,x)(t) = x,
Y(t,x)(0) = ∂xu0 X(t,x)(0) ,
Z(t,x)(0) = u0 X(t,x)(0) ,

24. Characteristics method
then
u(t, x) = Z(t,x)(t) (2.3)
defines the solution for the Cauchy problem with initial
condition u(0, x) = u0(x).

25. So for fixed t, small enough:
ϕt(J1
v) = (x(t, q0), y(t, q0), z(t, q0)) | q0 ∈ J1
v
= (ξ, ∂xu(t, ξ), u(t, ξ)) | ξ ∈ x(t, J1
v)
= J1
ut
But in general for t bigger, there is no f ∈ C1
(Rk
) s.t.
ϕt(J1
v) = J1
f.

26. Section 3
Generating Families

27. Let J1
(M) = T∗
M × R with the contact form α = dz − ydx.
Definition 1 (gfqi).
S ∈ C2
(M × Rq
) is a generating family quadratic at infinity
of the Legendrian submanifold Λ of J1
M if
0 is a regular value of the fiber derivative ∂ξS.
Λ = {(x, ∂xS(x, ξ), S(x, ξ)) : ∂ξS(x, ξ) = 0}
∃ non degenerate quadratic form Q, such that ∀K ⊂ M
compact |∂ξ(S(x, ξ) − Q(ξ))| is bounded on K × Rq
.

28. Theorem.
A Legendrian submanifold contact isotopic to the zero section
has a gfqi, unique up to the following operations S1 ∼ S2
Stabilitation S2(x, ξ, η) = S1(x, ξ) + q(η) with q a ndqf.
Diffeomorphism S2(x, ξ) = S1(x, ψ(x, ξ)) with ψ(x, ·) a
diffeomorphism ∀x ∈ M.

29. Section 4
Constructing generating families

30. Generating Functions
Definition 2.
Φ ∈ C2
(R2k+1
) is a generating function for a
contactomorphism ϕ : J1
Rk
→ J1
Rk
if 1 − ∂zΦ(x, Y, z) = 0
and
X − x = ∂Y Φ(x, Y, z) (cx)
Y − y = −∂xΦ(x, Y, z) − y∂zΦ(x, Y, z) (cy)
Z − z = (X − x)Y − Φ(x, Y, z) (cz)
if and only if ϕ(x, y, z) = (X, Y, Z).

31. Remark 1.
ϕ has compact support if and only if Φ does.
Proposition 1.
A contactomorphism ϕ : J1
Rk
→ J1
Rk
with I − dϕ(p) < 1
for all p ∈ J1
Rk
has a unique generating function.

32. Suppose:
1 H ∈ C2
c ([0, T] × J1
Rk
)
2 ϕt
is the contact isotopy defined by (Eq. Char.).
3 supp H ⊂ {(x, y, z) : |y| ≤ a},
4 cH = sup{|DHt(x, y, z)|, |D2
Ht(x, y, z)|},

33. Lemma 3.
If δH = log 2/(2 + a)cH, and 0 < t − s < δH, then ϕs,t
has a
unique g.f. Φs,t
and letting ϕs,τ
(q) = (x(τ), y(τ), z(τ)), then
Φs,t
(x(s), y(t), z(s))
=
t
s
( ˙x(τ)(y(t) − y(τ)) + H(τ, ϕs,τ
(q)))dτ, (4.1)
∂tΦs,t
(x(s), y(t), z(s)) = H(t, ϕs,t
(q)) (4.2)

34. Constructing generating families
(a) Let s = t0 < t1 < · · · < tN = t such that |ti+1 − ti| < δH,
Φj = Φtj−1,tj
, v ∈ CLip,2
(Rk
). Define S : Rk
× R2kn
→ R
Ss,t
(x; ξ) = v(x0) +
N
j=1
yj(xj − xj−1) − Φj(xj−1, yj, zj−1)
(4.3)
xN = x, ξ = (x0, . . . , xN−1, y1, . . . , yN ), and



z0 = v(x0),
zj = zj−1 + (xj − xj−1)yj − Φj(xj−1, yj, zj−1).

35. Constructing generating families
Defining
Q(ξ) = −yN xN−1 +
N−1
i=1
yi(xi − xi−1), (QF)
Ws,t
(x, ξ) = v(x0) + x · yN −
N
j=1
Φtj−1,tj
(xj−1, yj, ¯zj−1),
(CS)
we see that for v ∈ C2,Lip
(Rk
), Ss,t
(x, ξ) is a gfqi.

36. Constructing generating families
(b) Let τj = s + (τ − s)(tj − s)/(t − s), Φτ
j = Φτj−1,τj
, then
Ss,t
(τ, x; ξ) = v(x0) +
N
j=1
yj(xj − xj−1) − Φτ
j (xj−1, yj, ¯zj−1).
(4.4)
is a gfqi of ϕs,τ
(J1
v).

37. Constructing generating families
(c) For each critical point ξ of Ss,t
(τ, x; ·)
Ss,t
(τ, x, ξ)
= v(x(s)) +
τ
s
˙x(σ)y(σ) − H σ, ϕs,σ
(j1
v(x0)) dσ
(4.5)
where ϕs,σ
(j1
v(x0)) = (x(σ), y(σ), z(σ)), x(τ) = x.

38. Section 5
Clarke Calculus Setting

39. Clarke Generalized Derivative
For f ∈ Liploc(Rq
), we define the Clark (generalized)
derivative as
∂f(a) = co lim
n→∞
df(xn) | lim
n→∞
xn = a (CGD)

40. Clarke Generalized Derivative
Lemma 4 (Fermat Rule).
If f ∈ Liploc(Rq
), then
(a) if f has a local extreme value at x = a, then 0 ∈ ∂f(a);
(b) if 0 ∈ ∂f(a), there exists a direction v for f at x = a such
that
lim sup
t↓0
f(x + tv) − f(x)
t
< 0.

41. Generalized generating families
Proposition 2.
Suppose that in the Cauchy problem (C.P.F.O.),
v ∈ Liploc(Rk
) and define ∂v = {(x, y, v(x)) : y ∈ ∂v(x)}.
Thus Ss,τ
generates Lτ
= ϕs,τ
H (∂v) i.e.
Lτ
= {(x, ∂xSs,τ
(τ, x, ξ), Ss,t
(τ, x, ξ)) : 0 ∈ ∂ξSs,t
(τ, x, ξ)}
(5.1)
where ∂ denotes the Clarke’s generalized derivative.

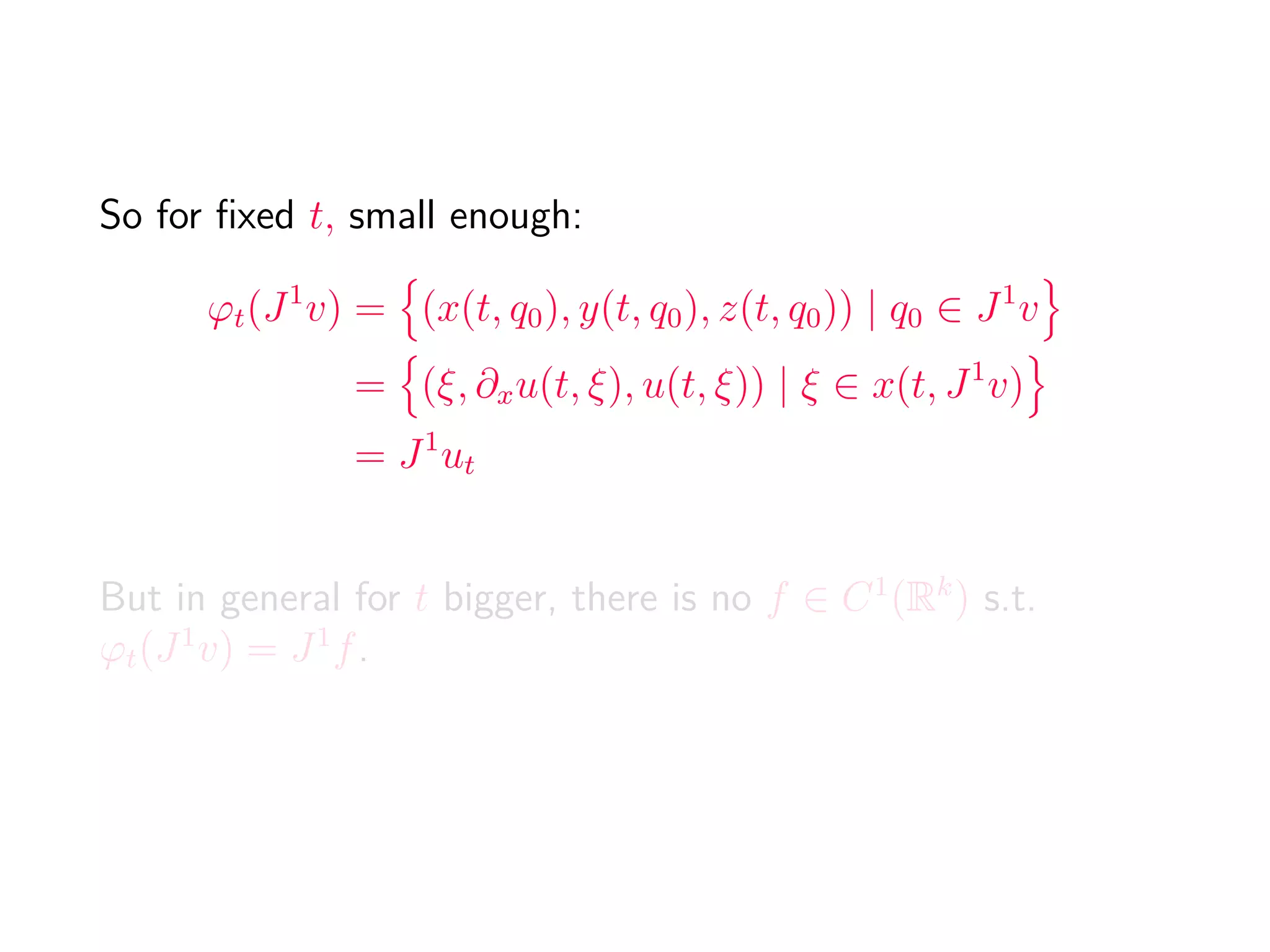
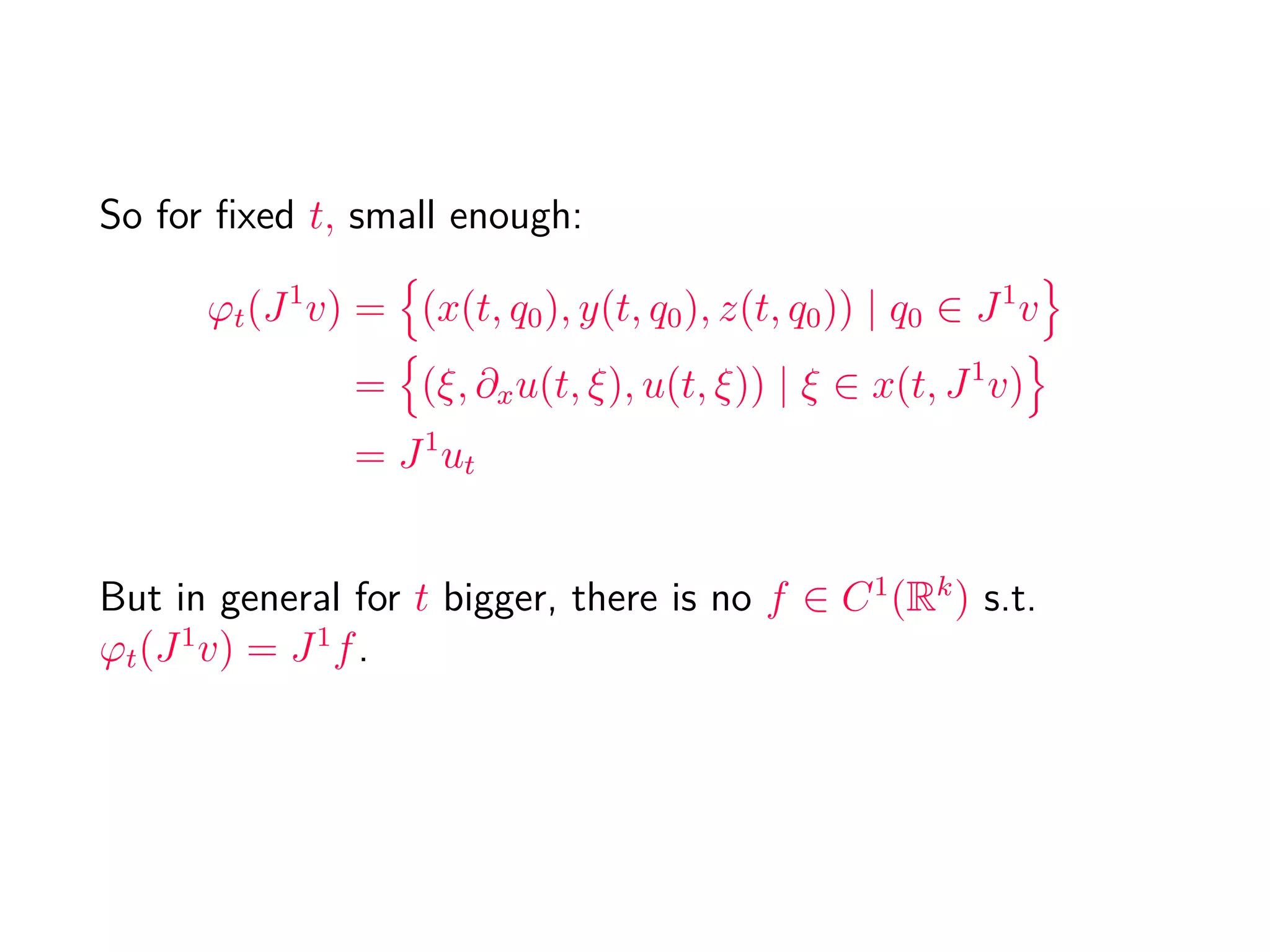
42. Generalized generating families
Let H ∈ C2
c ([0, T] × J1
Rk
), v ∈ CLip
(Rk
). Write
Ss,t
: [s, t] × Rk
× Rq
→ R given by (4.4) as
Ss,t
(τ, x, ξ) = Ws,t
(τ, x, ξ) + Q(ξ),
with Q, Ws,t
defined in (QF), (CS).
For each compact subset K of Rk
, the family of functions
{Ws,t
(τ, x, ·)}τ∈[s,t],x∈K is uniformly Lipschitz.

43. Generalized generating families
Moreover for any θ ∈ Cc(Rq
, [0, T]) identically 1 in a
neighborhhod of the origin with Dθ < 1, there exists a
constant aK > 1 such that for τ ∈ [s, t],
(x, ξ) → Ss,t
K (τ, x, ξ) = θ
ξ
aK
Ws,t
(τ, x, ξ) + Q(ξ) (5.2)
is a g.f.q.i. for
Lτ
K = Lτ
∩ π−1
(K)
= (x, ∂xSs,t
K (τ, x, ξ), Ss,t
K (τ, x, ξ)|0 ∈ ∂ξSs,t
K (τ, x, ξ)) ,
where π : J1
Rk
→ Rk
, (x, y, z) → x.

44. Section 6
Minimax Solution

45. Definition 5.
1 A sequence (um) in a manifold M is called of
Palais-Smale for E ∈ C1
(M) if |E(um)| ≤ c uniformly in
m and
limm→∞
DE(um) = 0.
2 We say that E satisfies Palais-Smale compactness
condition (PS) if every P-S sequence for E has a
strongly convergent subsequence.

46. Minimax Principle
Definition 1.
Let Φ : Rq
× [0, ∞) → Rq
be a semi-flow. A family F of
subsets of Rq
is called (positively) Φ-invariant if Φ(F, t) ∈ F
for all F ∈ F, t ≥ 0.

47. Minimax Principle
Suppose f ∈ C1
(Rq
) satisfies (PS). Also suppose F ⊂ P(Rq
)
is a collection of sets which is positively invariant with respect
to any continuous semi-flow
Φ : Rq
× [0, ∞) → Rq
satisfying:
(i) Φ(·, 0) = id(·);
(ii) Φ(·, t) is a homeomorphism of Rq
for any t ≥ 0; and
(iii) f (Φ(u, t)) is non-incresing in t for any u ∈ Rq
.

48. Minimax Principle
Theorem 2.
Under the above conditions, if
β = inf
F∈F
sup
u∈F
f(u)
is finite, β is a critical value of f.

49. Minimax Function
Let K ⊂ Rk
be a compact set, Ss,t
K ∈ C1
([s, t] × Rk
× Rq
) be
g.f.q.i. given as in (5.2) and Q(ξ) =
1
2
Pξ, ξ be the
associated quadratic form. As Ss,t
K = Q outside a compact set,
the critical levels of Ss,t
K are bounded. There is R(K) < 0 such
that for R < R(K), the sub–level set
(Ss,t
K )R
τ,x = ξ ∈ Rq
|Ss,t
k (τ, x; ξ) < R
is identical to the sub–level QR
.

50. Minimax Function
Definition 2.
Let j be the Morse index of Q and a > 0 large. We define Ga
as the set of continuous maps σ : Bj → Rq
, of the unit ball
Bj of dimension j, such that
σ(∂Bj) ⊂ Q−1
(−∞, −a).

51. Minimax Function
Let v ∈ CLip
(Rk
) H ∈ C2
c ([0, T] × J1
Rk
). Let
Ss,t
K ∈ C1
([s, t] × Rk
× Rq
) be as in (5.2). Let K ⊂ Rk
be
compact, a > −R(K).

52. Minimax Function
The function
(τ, x) ∈ [s, t] × Rk
→ Rs,τ
H,Kv(x) = inf
σ∈Ga
max
e∈Bj
Ss,t
K (τ, x, σ(e)),
has the following properties
(a) Rs,τ
H,Kv(x) is a critical value of ξ → Ss,t
K (τ, x, ξ);
(b) it is a Lipschitz function and therefore differentiable
almost everywhere a.e.;
(c) j1
Rs,τ
H,Kv is an a.e. section of the wave front
(τ, x, ∂xSs,t
K (τ, x, ξ), Ss,t
K (τ, x, ξ)) : 0 ∈ ∂ξSs,t
K (τ, x, ξ) .

53. Minimax Function
Let K, K ⊂ Rk
be compact. If x ∈ K ∩ K , τ ∈ [s, t] then
Rs,τ
H,K v(x) = Rs,τ
H,Kv(x).

54. Minimax Function
Rs,τ
H v(x) = inf
σ∈Ga
max
e∈Bj
Ss,t
(τ, x; σ(e)). (6.1)

55. Section 7
Iterated Minimax Solution

56. Viscosity solution
Definition 6.
(a) u ∈ C([0, T] × V ), V ⊂ Rk
is a viscosity subsolution (
supersolution) of
∂tu + H(t, x, ∂xu, u) = 0,
if ∀φ ∈ C1
(V × [0, T]), ∀(t0, x0) ∈ [0, T] × V at which
u − φ has a maximum (minimum)
∂tφ(t0, x0) + H(t0, x0, ∂xφ(t0, x0), u(t0, x0)) ≤ 0 (≥ 0).
(b) u is a viscosity solution if it is both a viscosity subsolution
and a supersolution.

57. Estimates
Proposition 3.
For [s, t] ⊂ [0, T] consider Rs,t
H : CLip
(Rk
) → CLip
(Rk
)
(a) ∂(Rs,t
H v) ≤ ( ∂v + |t − s| ∂xH )e|t−s| ∂zH
(b) |Rs,t
H v(x) − Rs,τ
H v(x)| ≤ C(H)|t − τ| H .
(c) If K ⊂ Rk
compact, ∃ ˜K ⊂ Rk
s.t.
Rs,t
H v − Rs,t
H w K ≤ v − w ˜K.

58. Iterated minimax operator
Given ζ = {0 = t0 < t1 < · · · < tn = T} define
|ζ| = max |ti+1 − ti|, and ζ(s) = max{ti : ti < s}, s ∈ [0, T].
Definition 7.
For 0 ≤ s < s ≤ T, let tj = ζ(s), ti = ζ(s ). We say that
Rs ,s
H,ζv(x) = R
tj,s
H ◦ · · · ◦ R
s ,ti+1
H v(x) (7.1)
is the iterated minimax solution.

59. Main result
Lemma 8.
(ζn)n sequence of partitions of [0, T] s,t. |ζn| → 0.
v ∈ CLip
(Rk
). Then {un(s, x) := R0,s
ζ v(x)} is equi-Lipschitz
in [0, T] × K.

60. Main result
Proposition 4.
For any sequence (ζn) of subdivisions of [0, T] s.t. |ζn| → 0,
K ⊂ Rk
, compact, {un := R0,s
ζn
v(x)} has a subsequence
converging uniformly on [0, T] × K to the viscosity solution of
(HJ).

61. Bibliography
V.I. Arnold Singularities of Caustics and Wave Fronts.
Mathematics and Its Applications (Soviet Series). Vol. 62.
Springer.
M Bhupal. Legendrian Intersections in the 1-Jet Bundle.
PhD Thesis. Mathematics Institute, University of
Warwick. 1998.
M. Bardi, I. Capuzzo Dolcetta. Optimal control and
viscosity solutions of Hamilton-Jacobi-Bellman equations.
Birkhausser, 1997.
Clarke, F.; Functional Analysis, Calculus of Variations and
Optimal Control. Springer-Verlag London, 2013.

62. Bibliography
Chaperon, M. On generating families. The Floer
Memorial volume. Birkh¨ausser, 1995, 284–296.
Chenciner A. Aspects g´eom´etriques de l’´etudes des chocs
dans les lois de conservation. Probl`ems d’´evolution non
lin´eaires, S´eminaire de Nice
M.G. Crandall, L.C. Evans, P.L. Lions, Some properties of
viscosity solutions of Hamilton-Jacobi equations. Trans.
Amer. Math. Soc. 282 (1984), no. 2, 487–502.
M.G. Crandall, P.L. Lions. On existence and uniqueness of
solutions of Hamilton-Jacobi equations. Nonlinear
Analysis: Theory, Methods & Applications, 10 No. 4
(1986) 353–370.

63. Bibliography
L. Evans. Partial Differential Equations. 2nd Edition.
American Mathematical Society. 2010.
Palais, R.S.; Critical point theory and the minimax
principle; Proceedings of Symposia in Pure Mathematics,
1970, XV, 185-212.
Struwe, Michael; Variational Methods: Applications to
Nonlinear Partial Differential Equations and Hamiltonian
Systems. Springer-Verlag, A Series of Modern Surveys in
Mathematics Vol. 34, 2008.
Wei, Q.; Viscosity solution of the Hamilton - Jacobi
equation by a limiting minimax method. Nonlinearity 27
(2014) 17–41.