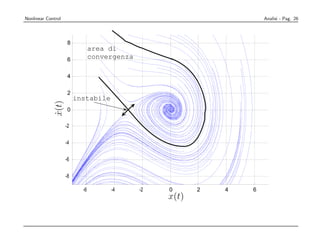
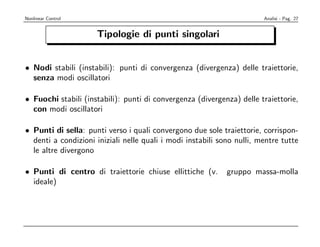
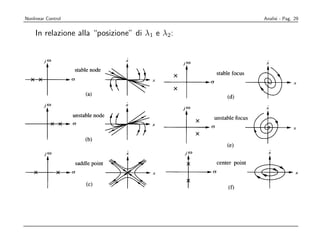
Il documento esplora il controllo nonlineare nei sistemi dinamici, descrivendo metodi di analisi e progettazione, con un focus su linearizzazione e controllo robusto. Viene fatta una distinzione tra modelli lineari e nonlineari, evidenziando le complessità dei sistemi nonlineari, come la presenza di molteplici punti di equilibrio e comportamento caotico. Si discute anche la stabilità, le traiettorie e le caratteristiche dei modelli attraverso esempi pratici come il pendolo e l'oscillatore di Van der Pol.



![Nonlinear Control Introduzione - Pag. 6
Esempio: pendolo
• Approccio lineare: trovare un modello
˙
x = Ax + Bu (con x = [θ θ]T ), valido
˙
in un intorno del punto di equilibrio x = 0
(es. ipotesi sin θ ≈ θ) e dimostrare che gli
autovalori di A sono a parte reale negativa
e/o trovare u = −Kx che li renda tali
• Approccio nonlineare: dato il modello
θ
x = f (x, u) valido ∀ x ∈ R2, dimostrare che
˙
M
x = 0 ` un punto a minima energia, pertanto
e
M ogni traiettoria dello stato tende a dissipare
l’energia del sistema fino a raggiungere tale
minimo (es. attriti) e/o trovare u = g(x)
che renda il sistema dissipativo (⇒ stabile)](https://image.slidesharecdn.com/nonlintutto2009-110812080238-phpapp01/85/Nonlin-tutto-2009-5-320.jpg)
![Nonlinear Control Introduzione - Pag. 6
Note sul lucido 6
Siano R la lunghezza del pendolo, M la massa appesa (trascurando quella dell’asta), g l’accelerazione di
gravit`, b il coefficiente di attrito viscoso alla cerniera e τ la coppia esercitata, ad esempio, da un motore elettrico
a
connesso alla cerniera, il modello dinamico del pendolo ` rappresentato dall’equazione:
e
2¨ ˙
M R θ + bθ + M gR sin θ = τ
˙
nella quale τ rappresenta l’ingresso di controllo. Considerando come variabili di stato x1 = θ e x2 = θ e
ponendo u = τ , si pu` ricondurre l’equazione precedente alla forma x = f (x, u):
o ˙
x1
˙ = x2
g b x + u
x2
˙ = − R sin x1 −
M R2 2 M R2
per cui x = [θ θ]T ed f (x, u) = [f1 (x, u) f2 (x, u)]T nella quale chiaramente
˙
f1 (x, u) = x2
g
f2 (x, u) = − R sin x1 − b 2 x2 + u 2 .
MR MR
I punti di equilibrio (x = 0) sono dati dalle soluzioni della equazione f (x) = 0, cio`:
˙ e
x2 = 0, sin x1 = 0](https://image.slidesharecdn.com/nonlintutto2009-110812080238-phpapp01/85/Nonlin-tutto-2009-6-320.jpg)
















































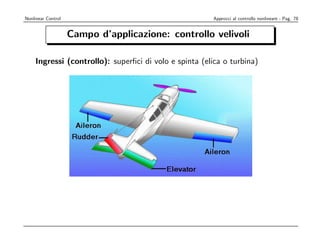
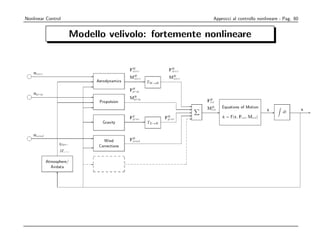



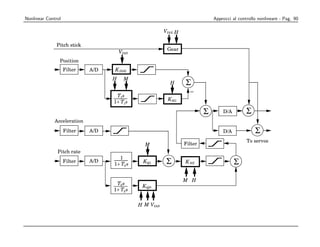
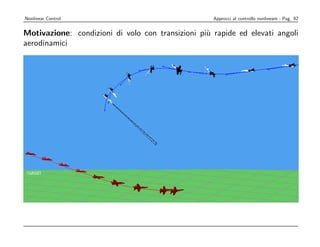
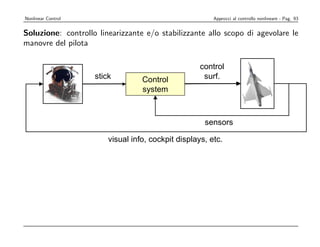
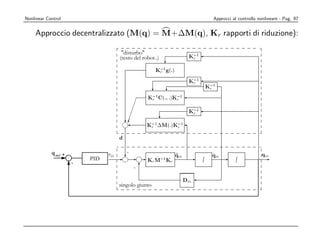
![Considereremo
Nonlinear Control ora il sistema di Navigazione, Guida e Controllo (NGC) del velivolo. nonlineare - Pag.
Approcci al controllo 88
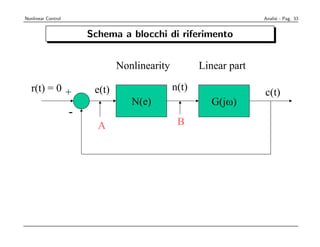
Lo schema classico di rappresentazione, come indicato nel testo [6], è il seguente:
Schema completo del sistema di navigazione:
Data-base
delle
traiettorie δe ,δa, δr, δth, (di riferimento) Disturbi(vento)
∆ψ, ∆H +
Selettore di Sistema Controllo Velivolo e
+
Navigazione di Guida + Attuatori
-
X,Y,H X,Y,H V,α,β,P,Q,R,φ,θ,n
X, Y, H
Sensori e Filtri di
Navigazione
Figura 2.2 Schema a blocchi funzionale del sistema NGC
Procediamo ora illustrando le funzionalità dei vari blocchi :](https://image.slidesharecdn.com/nonlintutto2009-110812080238-phpapp01/85/Nonlin-tutto-2009-82-320.jpg)














![Nonlinear Control Feedback Linearization - Pag. 109
Per un sistema in forma companion la legge di controllo nonlineare:
1
u= [v − f (x)]
b(x)
trasforma la dinamica in una serie di n integratori:
x(n) = v
per la quale ` sempre possible imporre una dinamica esponenzialmente
e
stabile, sia per problemi di regolazione che per problemi di inseguimento di una
traiettoria xd(t), con una legge di controllo del tipo (scelti opportuni Ki:
(n)
v = xd − K0e − K1e − · · · − Kn−1e(n−1)
˙
NOTA: devono essere disponibili tutte le derivate necessarie di xd(t)](https://image.slidesharecdn.com/nonlintutto2009-110812080238-phpapp01/85/Nonlin-tutto-2009-107-320.jpg)
![Nonlinear Control Feedback Linearization - Pag. 109
Note sul lucido 109
L’estensione ad un sistema MIMO (come un robot manipolatore) richiede ovviamente che la dinamica sia
espressa in modo vettoriale:
(n)
x = f (x) + b(x)u
linearizzabile tramite la legge di controllo:
−1
u=b (x)[v − f (x)]
Tuttavia, in questo caso la linearizzazione ` possibile solamente se la matrice b(x) ` invertibile
e e
n
∀ x ∈ Ω ⊆ R . Nelle applicazioni di robotica, come si ` visto, ci` ` garantito dalle propriet` strutturali
e o e a
meccaniche (matrice di inerzia) dei manipolatori.](https://image.slidesharecdn.com/nonlintutto2009-110812080238-phpapp01/85/Nonlin-tutto-2009-108-320.jpg)


![Nonlinear Control Feedback Linearization - Pag. 112
che permette di ottenere il sistema lineare:
z1
˙ = −2z1 + z2
z2
˙ = v
Tale sistema risulta essere controllabile (rank([b|Ab]) = 2), pertanto ` possibile assegnarne arbitrariamente
e
gli autovalori con una retroazione del tipo v = −k1 z1 − k2 z2 .](https://image.slidesharecdn.com/nonlintutto2009-110812080238-phpapp01/85/Nonlin-tutto-2009-112-320.jpg)

![Nonlinear Control Feedback Linearization - Pag. 113
Note sul lucido 113
Ad esempio, si consideri il sistema del terzo ordine:
x1
˙ = sin x2 + (x2 + 1)x3
x2
˙ = x5 + x3
1
2
x3
˙ = x1 + u
y = x1
In questo caso, derivando l’uscita si ottiene:
y = x1 = sin x2 + (x2 + 1)x3
˙ ˙
nella quale non compare l’ingresso u. Occorre quindi derivare l’uscita una seconda volta:
y = x2 cos x2 + x2 x3 + (x2 + 1)x3 = (x2 + 1)u + f1 (x)
¨ ˙ ˙ ˙
nella quale f1 (x) contiene tutti gli altri termini non legati all’ingresso. Chiaramente, questa dinamica pu` essere
o
trasformata in quella di un doppio integratore y = v con il controllo:
¨
1
u= [v − f1 (x)]
x2 + 1](https://image.slidesharecdn.com/nonlintutto2009-110812080238-phpapp01/85/Nonlin-tutto-2009-114-320.jpg)









![Nonlinear Control Feedback Linearization - Pag. 122
Supponendo ora di definire un diffeomorfismo avente la seguente struttura:
z = Φ(x) = [h Lf h L2 h
f ... Lr−1 h
f Φr+1(x) ... Φn(x)]
si ottiene il sistema trasformato:
z1
˙ = Lf h = z2
z2
˙ = L2 h
f = z3
...
zr−1
˙ = Lr−1 h
f = zr
zr
˙ = Lr h + Lb Lr−1 h u
f f
con uscita y = z1, linearizzabile con la legge di controllo descritta in precedenza.](https://image.slidesharecdn.com/nonlintutto2009-110812080238-phpapp01/85/Nonlin-tutto-2009-124-320.jpg)

![Nonlinear Control Feedback Linearization - Pag. 126
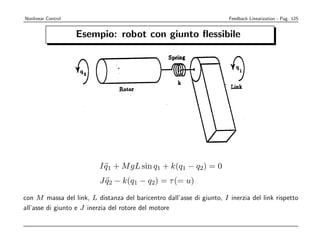
Le equazioni dinamiche sono riconducibili alla forma affine x = f + bu se
˙
poniamo x = [x1 x2 x3 x4]T = [q1 q1 q2 q2]T e:
˙ ˙
f = [x2 − MI sin x1 − k (x1 − x3)
gL
I x4 k
J (x1 − x3)]T
1 T
b = [0 0 0 J]
Ipotizzando di considerare come uscita y = x1 = q1, cio` la posizione
e
angolare del link, otteniamo che:
y
˙ = x1
˙ = x2
y
¨ = x2
˙ = − MI sin x1 − k (x1 − x3)
gL
I
y (3) = − MI x2 cos x1 − k (x2 − x4 )
gL
I
N. B .
(4) k k
y = ··· + I x4
˙ = a(x) + IJ u](https://image.slidesharecdn.com/nonlintutto2009-110812080238-phpapp01/85/Nonlin-tutto-2009-128-320.jpg)
![Nonlinear Control Feedback Linearization - Pag. 127
Il sistema ha quindi grado relativo ben definito (k/(I J) = 0 sempre!), pari
a 4, cio` all’ordine del sistema, che ` quindi linearizzabile completamente
e e
attraverso la legge di controllo:
IJ
u= [v − a(x)]
k
nella quale (ahinoi):
M gL M gL k k k k M gL
a(x) = sin x1(x2 +
2 cos x1 + ) + (x1 − x3)( + + cos x1)
I I I I I J I](https://image.slidesharecdn.com/nonlintutto2009-110812080238-phpapp01/85/Nonlin-tutto-2009-129-320.jpg)



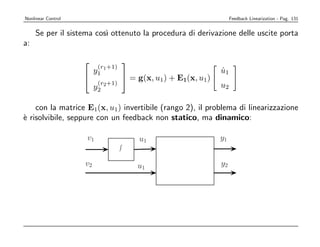



![Nonlinear Control Feedback Linearization - Pag. 136
Tipico modello cinematico: uniciclo
al example of nonholonomy: the rolling disk
y θ
x
alized coordinates q = (x, y,velocit` laterale sempre nulla ⇒ x sin θ − y cos θ = 0
Vincolo cinematico: θ) a ˙ ˙
x
˙ cos θ 0 y˙
rolling nonholonomic constraint y θ = sin = 0 v = tan θ
Modello cinematico x sin − y cos θ θ 0
˙ ˙ ˙
˙ ω
˙
x
θ 0 1
e velocities are contained in the null space of the constraint matrix
˙
con v = driving velocity e ω = steering velocity. In forma compatta q = G( v, con le
q)
ovvie sostituzioni q = [x y θ]T e v = [u ω]T cos θ 0
(q) = (sin θ − cos θ 0) =⇒ N (aT (q)) = span sin θ , 0
0 1
onfiguration q = (x , y , θ ) can be reached:](https://image.slidesharecdn.com/nonlintutto2009-110812080238-phpapp01/85/Nonlin-tutto-2009-138-320.jpg)
![Nonlinear Control Feedback Linearization - Pag. 138
Feedback linearization dell’uniciclo
Considerando come uscita di interesse y = [x y]T , si ottiene:
x
˙ cos θ 0 v
˙
y= =
y
˙ sin θ 0 ω
E(q)
con matrice di disaccoppiamento E(q) singolare (y influenzata solo da v).
Inserendo un integratore a monte di v, si ottiene:
˙ cos θ
v = ζ, ζ=a =⇒ ˙
y=ζ
sin θ
che ulteriormente derivata:](https://image.slidesharecdn.com/nonlintutto2009-110812080238-phpapp01/85/Nonlin-tutto-2009-140-320.jpg)

![Nonlinear Control Feedback Linearization - Pag. 140
Note sulla linearizzazione dell’uniciclo
• Il sistema ` linearizzabile con feedback dinamico, il quale aggiunge
e
sostanzialmente una ulteriore variabile di stato ζ
• Il modello completo dell’uniciclo ` di ordine 3, pi` il feedback dinamico = 4
e u
• Il modello linearizzato tramite feedback ` anch’esso di ordine 4 (con stato
e
[x y x y]T per cui la linearizzazione ` completa (ingresso-stato)
˙ ˙ e
• Il problema residuo consiste nell’evitare la singolarit` di E1(q, ζ), risolvi-
a
bile tramite inizializzazione dell’integratore e opportuna pianificazione delle
traiettorie](https://image.slidesharecdn.com/nonlintutto2009-110812080238-phpapp01/85/Nonlin-tutto-2009-142-320.jpg)
![Nonlinear Control Appendice su Feedback Linearization - Pag. 141
Appendice: strumenti matematici (algebra di
Lie)
Definizione 17 Dati due campi vettoriali f : Rn → Rn e g : Rn → Rn, si
definisce Lie bracket di f e g un terzo campo vettoriale ottenuto come segue:
∂g ∂f
[f , g] = f− g
∂x ∂x
La [f , g] ` indicata anche con adf g (dove ad = “adjoint”). Per estensione:
e
ad0 g = g
f
adi g = [f , adi−1 g]
f f i = 1, 2, . . .
L’operatore Lie bracket ` bilineare e anti-commutativo. Vale inoltre la seguente
e
identit` di Jacobi, data la funzione scalare smooth di x:
a
Ladf g h = Lf Lg h − Lg Lf h](https://image.slidesharecdn.com/nonlintutto2009-110812080238-phpapp01/85/Nonlin-tutto-2009-143-320.jpg)
![뫹 ~Dð mU¡“ë¦Î
î Îë “ Å ´ ~
•ƒ² ¨ X pš ¦4’xƒ~² ¦pš ¨ X ”
” Ì ” é ´ Ì ” Ë „Ê — É º –
õ¦Àgëgê ¹
ü ” ‘ o” “ i i –m
piüößj•f——Dq‰q€D¤ijfi‰˜ ˆs¨D×wl㘠‘U6j„Ã@|
– — ‘ ” h ‘ yr ˆ – ˆ e – ” –
yrr e ‘ ˆ ” w‘ r e “ È ” ‰
siDumn’€jx’fD¨xt‘ – w ˆ Çù ô ú õú ‚ ó } ó
De ê DÕrx”9¦D|ŠuDà˜™xg4g6j¤n‹H1Ž x¡ñ ¦ót¢á„18p„ö Â
‰ w – m ” † – ” û m e – ”‘ ‚ ” h
flussi sono commutativi. Si consideri ad esempio, una barca a vela che debba navigare controvento. Come noto,
e hIgƒsÚ¦s
Æ ¾À É Å e
Infatti, ` possibile dimostrare che la [f , g] di due campi vettoriali ` identicamente nulla se e solo se i loro
all’evoluzione ottenuta invertendo l’ordine di f e g (v. figura sottostante).
¥ ´ X # “ u6 ”² 0 # # # – ê u 6 ' ™ © # 0 # t t 6 V “ #
bEv8†hÂ%bd)idAÎA0¡)'FΡ§c¦A†)ƒd¡)©CvA¹A8(()'f8¡A%A
di f (γt ) per un tempo t e successivamente lungo le traiettorie di g (γt ) per un tempo s non sia equivalente
f g
# $ ' # t ! ' V ' # i6 u Å # $6 ©™ – ™ © ! © 2 # ‹ ' u © ' # 0 ' # $6 ™
„)ACvAf%S8)ƒ%)8EŒ„§Af)„Α)o)4%Œ£„¡8)U%vtA¹¡)S“H„§Af)©„«ê
e
o meno commutatativi, cio` se, partendo da un certo punto ∈Rn , l’evoluzione del punto lungo le traiettorie
! © 2 ‹ ' u © ' u 6 © u ' ~ 6 © @ $ © u 6 ' ' t 2 '™ #
™)©«)4%#Œ£ov8)ov§)¼0¡)»»7gz' Ad™zv§AA¦AAR¦¡A¯4)hEvtAoR%8)'
con notazione γt ). L’operatore Lie bracket permette di determinare se i flussi di due sistemi dinamici f e g siano
f © #
˙ ˙ e
i “ ° # 6 º – ë # c 2 ' #6 ` ™ © u t ' i ' t ! ' # © # t t © © @ ©
…s86¡%S§aÀggê ¹ d))¡5¯8uj)Ãv§6¡A76¡)ˆf¦1AfpACvS¡Q¯v(j¥d186A86Ax)A¡@
differenziale x = f (x) ` una curva γ : t → x(t), anch’essa di classe C ∞ , che viene chiamata flusso di f (anche
e
u 6 V © ©™ # t 6 0 # ' # ' # 2 ' 5 #6 ` ™ © #6 # @ © @ 26 # $ # u 26 ' 5 #
v7(p87d¯vAz§3%¦ACA¦ed)cA)¡R8uu)e%8AAdx)A¡¯§bd„©d)R§A)1Rvtƒt
Chiaramente, f ` un campo vettoriale. Per un qualsiasi campo vettoriale f ∈ C ∞ , la soluzione dell’equazione
˙ ˙
x = f (x) ü wr ” – m ”
Õx9sD|ƒD†
e ” ˆ‘ e ‰‘ ‰ wr – m ” † ” ˆ r – € ˜ – ” û m e ” ‘ ‚ ” h o yrr ˆ‘ Ä ü wr ” – m ”
Du¦iÆr záz¢j”9aD|ŠuDUDe0t‘s‡ß’U™‰xg4g6j– |q”fiã¢ÆiDeiß…j9aD|ƒD†
€D|j1Dum×—áUj”9pD|ŠuD†De0t‘sUe i’‹UÕx”9pl–|Šmlà€D|j1Du×—™`xg4g6jè”|q‚
ˆ e ‰ ˆ – e ‰‘ wr – m ” ” ˆ r h‘ € wr ” † ˆ e ‰ ˆ – m e ˜ – ” û m e – ‘
“linearizzabilit`” di un sistema dinamico. Si consideri un sistema dinamico del tipo:
a
” ü – ” à ‰‘ ‰ wr – m † e – m – € – ” û m e – ”‘ ‚ ” h
fhŽˆ6j„dtcDÕx”9»D|Šu”D߀ˆD|F‰¨ˆDuUß’˜™ßxg4g6jn‹¤1Ž §¡ñ ¦t¢á„1ó8}pó„ö  Žù ô óú õú ‚
Concettualmente, l’operatore Lie bracket ` molto legato alle caratteristiche di controllabilit` e
e a
| ¤
%)¤
Note sul lucido 141
§ ©§ ¥ £
¨˜Œ¨ ¦¤¢
Appendice su Feedback Linearization - Pag. 141 Nonlinear Control](https://image.slidesharecdn.com/nonlintutto2009-110812080238-phpapp01/85/Nonlin-tutto-2009-144-320.jpg)
![Nonlinear Control Appendice su Feedback Linearization - Pag. 142
la navigazione in tali condizioni ` possibile se la barca viene condotta con una manovra “zig-zagante”, con la
e
quale si riesce, approssimativamente, a dirigere la barca verso un punto altrimenti raggiungibile solo con una
rotta lineare in direzione contraria a quella del vento. Intuitivamente, si pu` affermare che, denominando f e g i
o
modelli dinamici della barca nelle due configurazioni di navigazione della rotta a zig-zag, il risultato di [f , g] sia,
approssimativamente, nullo.
Inoltre, se un sistema dinamico non libero ha una forma del tipo:
x = f (x) + b(x)u
˙
n−1
l’insieme dei campi vettoriali {b, adf b, . . . , adf b} permette di effettuare una analisi di controllabilit`
a
del sistema.
Infatti, ` possibile ricavare che per un sistema lineare x = Ax + bu, l’insieme precedente ` costituito
e ˙ e
2 n−1 n−1
dai vettori costanti {b, −A b, A b, . . . , (−1) A b}. Come noto, se il rango della matrice ottenuta
ponendo come colonne i vettori precedenti (a meno del segno) ` pari all’ordine del sistema, il sistema lineare
e
x = Ax + bu ` completamente controllabile.
˙ e
Analogamente, se i campi vettoriali {b, adf b, . . . , adn−1 b} sono linearmente indipendenti in un certo
f
Ω ⊆ Rn , significa che il sistema nonlineare x = f (x) + b(x)u ` controllabile in Ω.
˙ e](https://image.slidesharecdn.com/nonlintutto2009-110812080238-phpapp01/85/Nonlin-tutto-2009-145-320.jpg)
![Nonlinear Control Appendice su Feedback Linearization - Pag. 143
Definizione 18 Un insieme linearmente indipendente di campi vettoriali
{f1, f2, . . . , fm} definiti in Rn ` detto completamente integrabile se e so-
e
lo se esistono n − m funzioni scalari h1(x), h1(x), . . . , hn−m(x), le cui
∂hi/x siano linearmente indipendenti, che soddisfano il sistema di equazioni
differenziali parziali:
∂hi
fj = Lfj hi = 0
x
con 1 ≤ i ≤ n − m, 1 ≤ j ≤ m.
Definizione 19 Un insieme linearmente indipendente di campi vettoriali
{f1, f2, . . . , fm} definiti in Rn ` detto involutivo se e solo se esistono delle
e
funzioni scalari αijk : Rn → R tali che:
m
[fi, fj ] = αijk fk ∀i, j
k=1
Teorema 7 (Frobenius)
Un insieme linearmente indipendente di campi vettoriali {f1, f2, . . . , fm} definiti
in Rn ` completamente integrabile se e solo se ` involutivo
e e](https://image.slidesharecdn.com/nonlintutto2009-110812080238-phpapp01/85/Nonlin-tutto-2009-146-320.jpg)



![Nonlinear Control Appendice su Feedback Linearization - Pag. 146
n−1 T
z = Φ(x) = [z1 Lf z1 ... Lf z1 ]
Si noti che, mentre per le prime n − 1 nuove variabili di stato la dinamica ` quella di un integratore
e
zk = zk+1 , per l’ultima delle nuove variabili di stato, la dinamica ` del tipo:
˙ e
n n−1
zn = Lf z1 + Lb Lf
˙ u
˙
per cui il sistema trasformato z = fn (z) + bn (z) u ` in forma canonica di controllabilit` (companion).
e a
Finalmente, questo significa che il sistema ` linearizzabile ingresso-stato nel nuovo stato z scegliendo la legge
e
di controllo:
1 n
u= (v − Lf z1 )
Lb Ln−1 z1
f
Si noti che nel diffeomorfismo e nella legge di controllo cos` determinate ` rimasta una incognita da risolvere: z1 ,
ı e
che ` sia una nuova variabile di stato, ma anche (soprattutto) una funzione di x. Per ottenere tale funzione,
e
occorre ricordare che, nel teorema sulla linearizzabilit`, l’insieme involutivo nella condizione 2 ha un elemento in
a
meno di quello nella condizione 1. Questo significa che la funzione z1 (x) deve soddisfare il sistema di equazioni:
Ladi b z1 = 0 i = 0, . . . , n − 2
f
L z = 0
adn−1 b 1
f](https://image.slidesharecdn.com/nonlintutto2009-110812080238-phpapp01/85/Nonlin-tutto-2009-150-320.jpg)
![Nonlinear Control Appendice su Feedback Linearization - Pag. 147
Linearizzazione ingresso-stato: procedura
1. Dato il sistema x = f (x) + b(x)u (con f e b smooth), costruire il set
˙
{b, adf b, . . . , adn−1 b} e verificare controllabilit` e involutivit`
f a a
2. Trovare la z1(x) t.c.:
Ladi b z1 = 0 i = 0, dots, n − 2
f
Ladn−1 b z1 = 0
f
3. Costruire la trasformazione dello stato
z = Φ(x) = [z1 Lf z1 ... Ln−1 z1]T
f
e la legge di controllo
1
u= (−Ln z1 + v)
f
Lb Ln−1 z1
f](https://image.slidesharecdn.com/nonlintutto2009-110812080238-phpapp01/85/Nonlin-tutto-2009-151-320.jpg)
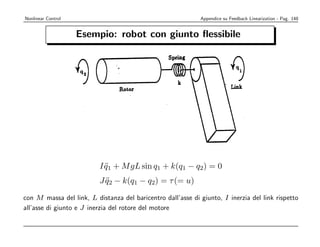
![Nonlinear Control Appendice su Feedback Linearization - Pag. 149
Poniamo x = [q1 q1
˙ q2 q2]T e:
˙
f = [x2 − MI sin x1 − k (x1 − x3)
gL
I x4 k
J (x1 − x3)]T
1 T
b = [0 0 0 J]
dalle quali:
k
0 0 0 − IJ
k
0 0 0
IJ
[b adf b ad2 b ad3 b] =
f f 1 k
0
J 0 −J2
1 k
J 0 −J2 0
che ha rango 4 se k 0 e IJ ∞, mentre l’involutivit` delle prime tre colonne
a
` garantita dal fatto che sono costanti
e](https://image.slidesharecdn.com/nonlintutto2009-110812080238-phpapp01/85/Nonlin-tutto-2009-153-320.jpg)

![Nonlinear Control Sliding Mode - Pag. 152
Sistemi a Struttura Variabile (VSS)
In generale, un sistema con:
x = f (x, u, t),
˙
u = [u1(x, t) u2(x, t) . . . um(x, t)]T
u+(x, t) se
i si(x) 0
ui = −
ui (x, t) se si(x) 0
s(x) = [s1(x) s2(x) . . . sm(x)]T
` un VSS la cui struttura varia in modo discontinuo in corrispondenza di m
e
superfici (si(x) = 0) nello spazio degli stati.](https://image.slidesharecdn.com/nonlintutto2009-110812080238-phpapp01/85/Nonlin-tutto-2009-156-320.jpg)
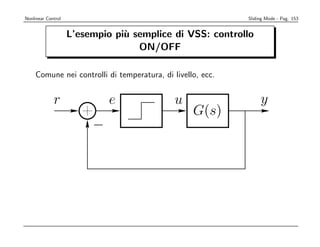


![Nonlinear Control Sliding Mode - Pag. 157
Progetto di controllo in Sliding Mode
Si consideri il sistema SISO in forma canonica di controllabilit` (companion):
a
x(n) = f (x, t) + b(x, t)u + d(t)
con f (x, t) e b(x, t) non note con precisione e d(t) un disturbo limitato.
NOTA: tale dinamica ` tipica nelle applicazioni industriali di motion control, con x posizione
e
di un cinematismo, u coppia di un motore e x = [x x . . . x(n−1)]T vettore di stato.
˙
Si desidera risolvere il problema di inseguimento della traiettoria xd(t) =
(n−1) T
[xd xd . . . xd
˙ ] in modo robusto rispetto a d e all’imprecisione di f e b.
Ponendo e = x − xd (errore di posizione) ed e = x − xd = [e e . . . e(n−1)]T
˙
vettore “errore di inseguimento”, il problema di tracking si pu` ricondurre a
o
quello di stabilizzazione di una superficie di sliding](https://image.slidesharecdn.com/nonlintutto2009-110812080238-phpapp01/85/Nonlin-tutto-2009-161-320.jpg)




![Nonlinear Control Sliding Mode - Pag. 162
Poich` f non ` nota in modo preciso, la migliore approssimazione disponibile
e e
del controllo “ideale” `:
e
u = xd − f − λe
¨ ˙
Inoltre, per imporre che il sistema sia in Sliding Mode su s = 0, occorre
aggiungere a u un termine discontinuo:
u = u − k sign(s)
con k = k(x, x, t) tale da garantire l’attrattivit` di s = 0:
˙ a
1 d 2
s = s · s = [f − f − k sign(s)] · s = (f − f )s − k|s| ≤ −η|s|
˙
2 dt
perci` k ≥ F + η
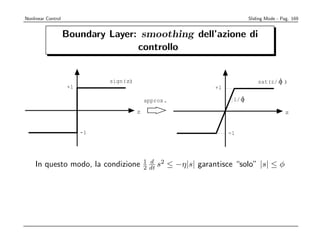
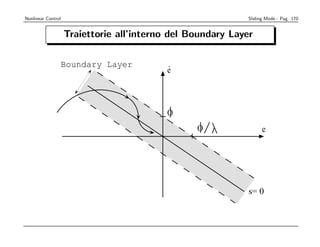
o](https://image.slidesharecdn.com/nonlintutto2009-110812080238-phpapp01/85/Nonlin-tutto-2009-166-320.jpg)


![Nonlinear Control Sliding Mode - Pag. 164
Estensioni delle considerazioni di robustezza - 1
Se il controllo entra nella dinamica moltiplicato per una funzione incerta
b(x, t) ` necessario ipotizzarne i limiti:
e
0 bmin ≤ b ≤ bmax
√
La migliore stima di b ` la media geometrica b =
e bmin bmax, per cui la
legge di controllo diventa:
u = b−1[u − k sign(s)]
con:
k ≥ β(F + η) + (β − 1)|u|
bmax
eβ= bmin chiamato margine di guadagno (β −1 ≤ b/b ≤ β)](https://image.slidesharecdn.com/nonlintutto2009-110812080238-phpapp01/85/Nonlin-tutto-2009-169-320.jpg)
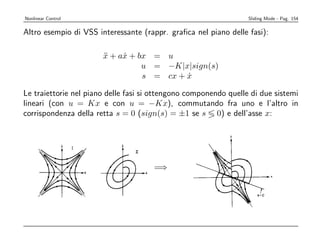
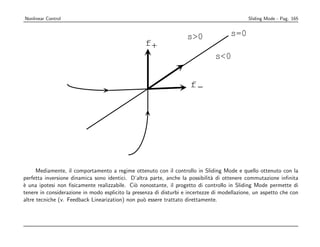
![Nonlinear Control Sliding Mode - Pag. 164
Note sul lucido 164
Per un sistema in forma canonica di controllabilit`:
a
(n)
x = f (x) + b(x)u
` evidente che la legge di controllo ideale per ottenere inseguimento perfetto e, di conseguenza, s(t) = 0 ∀ t,
e
sarebbe quella basata sulla inversione dinamica (precisa):
1
u= [¨d − f (xd )]
x
b(x)
Poich` tale controllo non ` realizzabile direttamente a causa dei disturbi e delle incertezze su f e b, essa
e e
viene ottenuta attraverso una sequenza di commutazioni a frequenza infinita tra le traiettorie di due differenti
dinamiche (strutture) dello stato, traiettorie tangenti ai vettori (in R2 ):
f+ = [ x f + b u + ]T
˙
f− = [ x f + b u − ]T
˙
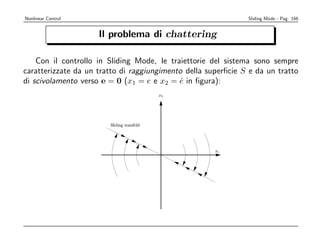
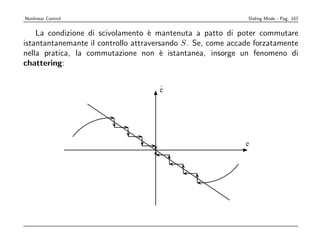
come rappresentato graficamente nella figura seguente.](https://image.slidesharecdn.com/nonlintutto2009-110812080238-phpapp01/85/Nonlin-tutto-2009-170-320.jpg)





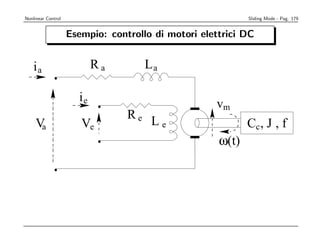
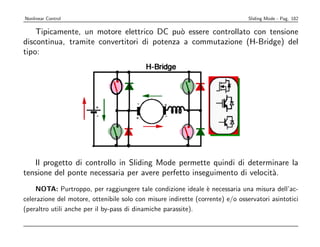
![Nonlinear Control Sliding Mode - Pag. 176
Concludendo, si pu` progettare la legge di controllo:
o
u = b−1[u − k sign(s)]
con s = x1 + λx2 e:
k ≥ β(F + η) + (β − 1)|u|
2
Mmax Rmax
β= 2
Mmin Rmin
che in questo caso diventa:
k ≥ β(k1|x2| + η) + (β − 1)(k2 + k3|x2|) = k1 + k2|x2|](https://image.slidesharecdn.com/nonlintutto2009-110812080238-phpapp01/85/Nonlin-tutto-2009-181-320.jpg)