Il documento descrive l'interpolazione polinomiale utilizzando il metodo di Newton delle differenze divise, spiegando come calcolare un polinomio interpolatore a partire da un insieme di punti. Viene fornito un algoritmo in linguaggio C per implementare il metodo e diverse applicazioni pratiche con esempi dettagliati di interpolazione. La costruzione del polinomio richiede l'elaborazione di tabelle delle differenze divise e mostra i risultati in un formato visivo.

![INTERPOLAZIONE POLINOMIALE
Metodo di Newton ‐ Differenze divise
L’interpolazione polinomiale è un metodo di calcolo mediante il quale, data una funzione y = ƒ(x) e
dati i valori numerici che tale funzione assume per x a determinati valori x1, x2, ..., xn, si può
determinare con buona approssimazione il valore numerico di ƒ(x) per x = x0 con x1<x0<xn e x0 ≠ xi
(i = 2, 3, ..., xn). Il metodo di Newton riconduce l’interpolazione a un calcolo di differenze, che si
conducono alla formula di Taylor.
Il polinomio interpolatore Pn(x) ha la seguente struttura (più avanti vedremo come costruirla):
Pn(x) = a0 + a1⋅(x ‐ x0) + a2⋅(x ‐ x0)⋅(x ‐ x1) + ... + an⋅(x ‐ x0)⋅(x ‐ x1)⋅...⋅(x ‐ xn‐1)
dove i valori ai rappresentano le differenze divise, rapporti incrementali che si definiscono sugli
n+1 punti (x0, x1, ..., xn)
ƒ(x0) i = 0
ai = ƒ[x0, ..., xi] = ‐
(ƒ[x1, ..., xi] ‐ ƒ[x0, ..., xi‐1])/( xi ‐ x0) i > 0
Se si considera il caso generale di n+1 punti (x0, ..., xn), la differenza divisa di ordine n risulta
ƒ[x0, ..., xn] = (ƒ[x1, ...,xn] ‐ ƒ[x0, ..., xn‐1] )/(xn ‐ x0)
La differenza divisa risulta indipendente rispetto alle permutazioni in quanto dipende
esclusivamente dai punti e non dall’ordine in cui questi si trovano.](https://image.slidesharecdn.com/metododinewton-121225150943-phpapp02/85/Metodo-di-Newton-2-320.jpg)
![I valori delle differenze divise associate agli n+1 punti xi ed i coefficienti del polinomio
interpolatore si ottengono mediante la costruzione di un’opportuna tabella contenente i valori
degli stessi punti xi e delle funzioni ƒ[x0, ..., xn]:
ordine 0 ordine 1 ordine 2 ... ordine n
xi yi=ƒ(xi)
x0 ƒ(x0)
x1 ƒ(x1) ƒ[x0, x1]
x2 ƒ(x2) ƒ[x1, x2] ƒ[x0, x1, x2]
. . . . .
. . . . .
x n ƒ(xn) ƒ[xn‐1, xn] ƒ[xn‐2, ..., xn] ... ƒ[x0, ..., xn]
Dalla tabella, che richiede n2 somme algebriche e n2/2 divisioni, si estrapolano gli elementi della
diagonale; questi rappresentano i coefficienti del polinomio interpolatore, che avrà, come
abbiamo visto prima, la seguente forma:
Pn(x) = a0 + a1⋅(x ‐ x0) + a2⋅(x ‐ x0)⋅(x ‐ x1) + ... + an⋅(x ‐ x0)⋅(x ‐ x1)⋅...⋅(x ‐ xn‐1)
con a0 = ƒ(x0), a1 = ƒ[x0, x1], a2 = ƒ[x0, x1, x2], ..., an = ƒ[x0, x1, ..., xn]. La costruzione di tale polinomio
richiede invece n moltiplicazioni e 2n somme.
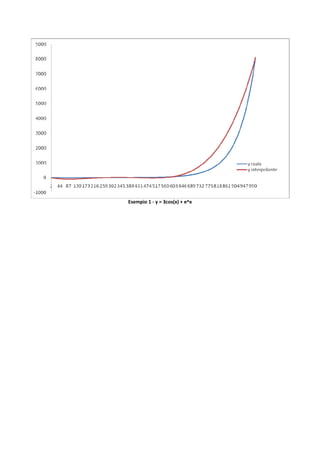
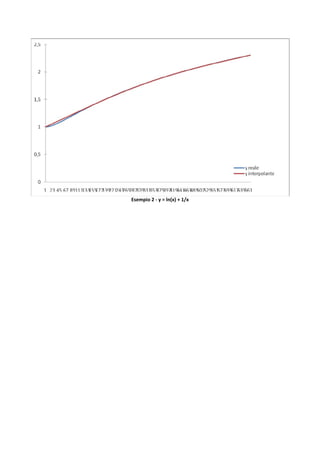
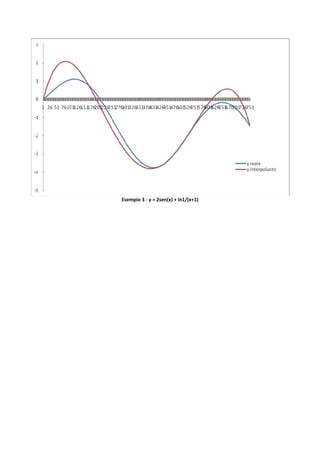
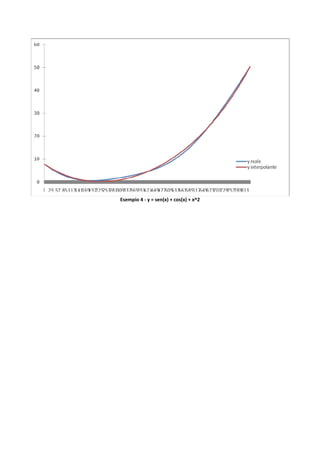
Nelle pagine a seguire verranno presentati l’algoritmo risolutivo del metodo delle differenze
divise, tradotto in linguaggio C, ed alcuni esempi di interpolazione attraverso il metodo di Newton,
ciascuno dei quali sarà corredato dalle schermate di visualizzazione dell’algoritmo sopra riportato
e da opportuni grafici di confronto tra funzione reale e polinomio interpolante.](https://image.slidesharecdn.com/metododinewton-121225150943-phpapp02/85/Metodo-di-Newton-3-320.jpg)
![/*******************************************************************************
Il programma effettua l'interpolazione polinomiale di una serie di numeri inseriti da tastiera
attraverso il Metodo di Newton delle Differenze Divise. L'algoritmo visualizza in uscita i risultati
del processo di calcolo, quali tabella degli ordini ed elementi della diagonale principale utilizzati
come coefficienti del polinomio interpolatore, ed il polinomio stesso.
Autore:
‐ Sergio Porcu
*******************************************************************************/
#include<stdio.h>
#include<iostream.h>
#include<math.h>
#include<conio.h>
#define N 10
main()
{
/* Dichiarazione delle variabili */
float x[N]; /* Vettore contenente i valori delle x dei punti */
float y[N]; /* Vettore contenente i valori delle y dei punti */
float f[N]; /* Vettore contenente i valori delle funzioni */
float app[N]; /* Vettore di appoggio contenente i valore delle funzioni */
float diagon[N]; /* Vettore contenente i valori della diagonale principale */
int cont,i,j; /* Contatori */
int num; /* Numero di punti da interpolare */
int salto,passo; /* Variabili di comodo */
/* Inizializzazione delle variabili */
num=0;
clrscr();
/* Inserimento dei valori dei punti da interpolare */
puts("ttInterpolazione dei punti con il metodo delle ");
puts("tt differenze divise (metodo di Newton)n");
printf("Quanti punti vuoi interpolare? : ");
cin>>num;
passo=(num‐1);
for(cont=0;cont<num;cont++) /* Ciclo di inserimento */
{
printf("Inserisci il valore x del %d° punto : ",cont+1);
cin>>x[cont];
printf("Inserisci il valore y del %d° punto : ",cont+1);
cin>>y[cont];
}
/* Inizializzazione del vettore contenete i valori delle funzioni */
for(cont=0;cont<num;cont++)](https://image.slidesharecdn.com/metododinewton-121225150943-phpapp02/85/Metodo-di-Newton-4-320.jpg)
![{
f[cont]=y[cont];
}
/* Inizio elaborazione dati */
clrscr();
printf("Scansione dei risultati elaborati dal calcolatore : n");
printf("Colonna delle differenze divise di ordine 0n");
for(i=0;i<num;i++)
{
cout<<f[i];
printf("n");
}
for(i=0;i<num;i++) /* Scansione dei punti */
{
/* Memorizzazione degli elementi della diagonale */
diagon[i]=f[i];
salto=i+1;
for(j=i+1;j<num;j++) /* Ciclo di calcolo */
{
if(j==i+1)
printf("Colonna delle differenze divise di ordine %dn",i+1);
if(x[j]!=x[j‐salto]) /* Controllo di eventuali errori di inserimento */
{
app[j]=(f[j]‐f[j‐1])/(x[j]‐x[j‐salto]);
}
else
{
clrscr();
printf("Errore di inserimento dati:n");
printf("i punti inseriti non appartengono ad una funzione ");
printf("continua!a");
return ‐1;
}
}
for(j=i+1;j<num;j++)
{
f[j]=app[j];
cout<<f[j];
printf("n");
}
}
/* Fine elaborazione dati */
/* Visualizzazione finale dei dati */
printf("n");
printf("I valori della diagonale sono : n");](https://image.slidesharecdn.com/metododinewton-121225150943-phpapp02/85/Metodo-di-Newton-5-320.jpg)
![for(i=0;i<num;i++)
{
cout<<diagon[i];
printf("n");
}
printf("n");
printf("P%d(x)=",(num‐1));
cout<<diagon[0];
for(i=1;i<num;i++)
{
if(diagon[i]>=0)
printf("+");
cout<<diagon[i];
for(j=1;j<=num‐passo;j++)
{
printf("(x");
if(x[j‐1]>=0)
printf("‐");
else
printf("+");
cout<<abs(x[j‐1]);
printf(")");
}
passo‐‐;
}
return 0;
}](https://image.slidesharecdn.com/metododinewton-121225150943-phpapp02/85/Metodo-di-Newton-6-320.jpg)