1. Tehtävä
Laske funktion f(x) = x2 + 2x – 8 nollakohdat.

2. On määritettävä funktion f(x) = x2 + 2x – 8 nollakohdat.

3. On määritettävä funktion f(x) = x2 + 2x – 8 nollakohdat.
Eli ratkaistava yhtälö x2 + 2x – 8 = 0

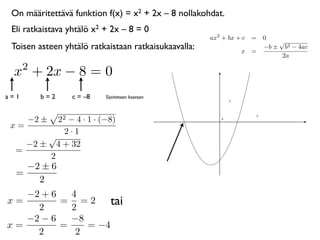
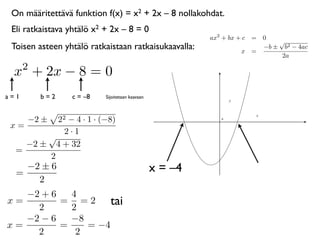
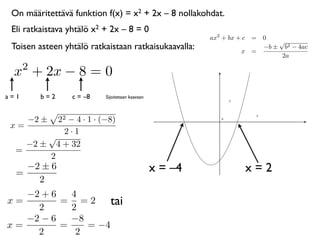
4. On määritettävä funktion f(x) = x2 + 2x – 8 nollakohdat.
Eli ratkaistava yhtälö x2 + 2x – 8 = 0
Toisen asteen yhtälö ratkaistaan ratkaisukaavalla:

5. On määritettävä funktion f(x) = x2 + 2x – 8 nollakohdat.
Eli ratkaistava yhtälö x2 + 2x – 8 = 0
ax2 + bx + c = 0
√
Toisen asteen yhtälö ratkaistaan ratkaisukaavalla: x =
−b ± b2 − 4ac
2a

6. On määritettävä funktion f(x) = x2 + 2x – 8 nollakohdat.
Eli ratkaistava yhtälö x2 + 2x – 8 = 0
ax2 + bx + c = 0
√
Toisen asteen yhtälö ratkaistaan ratkaisukaavalla: x =
−b ± b2 − 4ac
2a
2
x + 2x − 8 = 0

7. On määritettävä funktion f(x) = x2 + 2x – 8 nollakohdat.
Eli ratkaistava yhtälö x2 + 2x – 8 = 0
ax2 + bx + c = 0
√
Toisen asteen yhtälö ratkaistaan ratkaisukaavalla: x =
−b ± b2 − 4ac
2a
2
x + 2x − 8 = 0

8. On määritettävä funktion f(x) = x2 + 2x – 8 nollakohdat.
Eli ratkaistava yhtälö x2 + 2x – 8 = 0
ax2 + bx + c = 0
√
Toisen asteen yhtälö ratkaistaan ratkaisukaavalla: x =
−b ± b2 − 4ac
2a
2
x + 2x − 8 = 0
a=1

9. On määritettävä funktion f(x) = x2 + 2x – 8 nollakohdat.
Eli ratkaistava yhtälö x2 + 2x – 8 = 0
ax2 + bx + c = 0
√
Toisen asteen yhtälö ratkaistaan ratkaisukaavalla: x =
−b ± b2 − 4ac
2a
2
x + 2x − 8 = 0
a=1

10. On määritettävä funktion f(x) = x2 + 2x – 8 nollakohdat.
Eli ratkaistava yhtälö x2 + 2x – 8 = 0
ax2 + bx + c = 0
√
Toisen asteen yhtälö ratkaistaan ratkaisukaavalla: x =
−b ± b2 − 4ac
2a
2
x + 2x − 8 = 0
a=1 b=2

11. On määritettävä funktion f(x) = x2 + 2x – 8 nollakohdat.
Eli ratkaistava yhtälö x2 + 2x – 8 = 0
ax2 + bx + c = 0
√
Toisen asteen yhtälö ratkaistaan ratkaisukaavalla: x =
−b ± b2 − 4ac
2a
2
x + 2x − 8 = 0
a=1 b=2

12. On määritettävä funktion f(x) = x2 + 2x – 8 nollakohdat.
Eli ratkaistava yhtälö x2 + 2x – 8 = 0
ax2 + bx + c = 0
√
Toisen asteen yhtälö ratkaistaan ratkaisukaavalla: x =
−b ± b2 − 4ac
2a
2
x + 2x − 8 = 0
a=1 b=2 c = –8

13. On määritettävä funktion f(x) = x2 + 2x – 8 nollakohdat.
Eli ratkaistava yhtälö x2 + 2x – 8 = 0
ax2 + bx + c = 0
√
Toisen asteen yhtälö ratkaistaan ratkaisukaavalla: x =
−b ± b2 − 4ac
2a
2
x + 2x − 8 = 0
a=1 b=2 c = –8 Sijoitetaan kaavaan

14. On määritettävä funktion f(x) = x2 + 2x – 8 nollakohdat.
Eli ratkaistava yhtälö x2 + 2x – 8 = 0
ax2 + bx + c = 0
√
Toisen asteen yhtälö ratkaistaan ratkaisukaavalla: x =
−b ± b2 − 4ac
2a
2
x + 2x − 8 = 0
a=1 b=2 c = –8 Sijoitetaan kaavaan
−2 ± 22 − 4 · 1 · (−8)
x=
2·1

15. On määritettävä funktion f(x) = x2 + 2x – 8 nollakohdat.
Eli ratkaistava yhtälö x2 + 2x – 8 = 0
ax2 + bx + c = 0
√
Toisen asteen yhtälö ratkaistaan ratkaisukaavalla: x =
−b ± b2 − 4ac
2a
2
x + 2x − 8 = 0
a=1 b=2 c = –8 Sijoitetaan kaavaan
−2 ±22 − 4 · 1 · (−8)
x=
2·1
√
−2 ± 4 + 32
=
2

16. On määritettävä funktion f(x) = x2 + 2x – 8 nollakohdat.
Eli ratkaistava yhtälö x2 + 2x – 8 = 0
ax2 + bx + c = 0
√
Toisen asteen yhtälö ratkaistaan ratkaisukaavalla: x =
−b ± b2 − 4ac
2a
2
x + 2x − 8 = 0
a=1 b=2 c = –8 Sijoitetaan kaavaan
−2 ±22 − 4 · 1 · (−8)
x=
2·1
√
−2 ± 4 + 32
=
2
−2 ± 6
=
2

17. On määritettävä funktion f(x) = x2 + 2x – 8 nollakohdat.
Eli ratkaistava yhtälö x2 + 2x – 8 = 0
ax2 + bx + c = 0
√
Toisen asteen yhtälö ratkaistaan ratkaisukaavalla: x =
−b ± b2 − 4ac
2a
2
x + 2x − 8 = 0
a=1 b=2 c = –8 Sijoitetaan kaavaan
−2 ±22 − 4 · 1 · (−8)
x=
2·1
√
−2 ± 4 + 32
=
2
−2 ± 6
=
2
−2 + 6 4
x= = =2
2 2

18. On määritettävä funktion f(x) = x2 + 2x – 8 nollakohdat.
Eli ratkaistava yhtälö x2 + 2x – 8 = 0
ax2 + bx + c = 0
√
Toisen asteen yhtälö ratkaistaan ratkaisukaavalla: x =
−b ± b2 − 4ac
2a
2
x + 2x − 8 = 0
a=1 b=2 c = –8 Sijoitetaan kaavaan
−2 ±22 − 4 · 1 · (−8)
x=
2·1
√
−2 ± 4 + 32
=
2
−2 ± 6
=
2
−2 + 6 4
x=
2
= =2
2
tai

19. On määritettävä funktion f(x) = x2 + 2x – 8 nollakohdat.
Eli ratkaistava yhtälö x2 + 2x – 8 = 0
ax2 + bx + c = 0
√
Toisen asteen yhtälö ratkaistaan ratkaisukaavalla: x =
−b ± b2 − 4ac
2a
2
x + 2x − 8 = 0
a=1 b=2 c = –8 Sijoitetaan kaavaan
−2 ±22 − 4 · 1 · (−8)
x=
2·1
√
−2 ± 4 + 32
=
2
−2 ± 6
=
2
−2 + 6 4
x=
2
= =2
2
tai
−2 − 6 −8
x= = = −4
2 2

20. On määritettävä funktion f(x) = x2 + 2x – 8 nollakohdat.
Eli ratkaistava yhtälö x2 + 2x – 8 = 0
ax2 + bx + c = 0
√
Toisen asteen yhtälö ratkaistaan ratkaisukaavalla: x =
−b ± b2 − 4ac
2a
2
x + 2x − 8 = 0
a=1 b=2 c = –8 Sijoitetaan kaavaan
−2 ±22 − 4 · 1 · (−8) 0
x=
2·1
√
−2 ± 4 + 32
=
2
−2 ± 6
=
2
−2 + 6 4
x=
2
= =2
2
tai
−2 − 6 −8
x= = = −4
2 2

21. On määritettävä funktion f(x) = x2 + 2x – 8 nollakohdat.
Eli ratkaistava yhtälö x2 + 2x – 8 = 0
ax2 + bx + c = 0
√
Toisen asteen yhtälö ratkaistaan ratkaisukaavalla: x =
−b ± b2 − 4ac
2a
2
x + 2x − 8 = 0
a=1 b=2 c = –8 Sijoitetaan kaavaan
−2 ±22 − 4 · 1 · (−8) 0
x=
2·1
√
−2 ± 4 + 32
=
2
−2 ± 6
=
2
−2 + 6 4
x=
2
= =2
2
tai
−2 − 6 −8
x= = = −4
2 2

22. On määritettävä funktion f(x) = x2 + 2x – 8 nollakohdat.
Eli ratkaistava yhtälö x2 + 2x – 8 = 0
ax2 + bx + c = 0
√
Toisen asteen yhtälö ratkaistaan ratkaisukaavalla: x =
−b ± b2 − 4ac
2a
2
x + 2x − 8 = 0
a=1 b=2 c = –8 Sijoitetaan kaavaan
−2 ±22 − 4 · 1 · (−8) 0
x=
2·1
√
−2 ± 4 + 32
=
2
=
−2 ± 6 x = –4
2
−2 + 6 4
x=
2
= =2
2
tai
−2 − 6 −8
x= = = −4
2 2

23. On määritettävä funktion f(x) = x2 + 2x – 8 nollakohdat.
Eli ratkaistava yhtälö x2 + 2x – 8 = 0
ax2 + bx + c = 0
√
Toisen asteen yhtälö ratkaistaan ratkaisukaavalla: x =
−b ± b2 − 4ac
2a
2
x + 2x − 8 = 0
a=1 b=2 c = –8 Sijoitetaan kaavaan
−2 ±22 − 4 · 1 · (−8) 0
x=
2·1
√
−2 ± 4 + 32
=
2
=
−2 ± 6 x = –4
2
−2 + 6 4
x=
2
= =2
2
tai
−2 − 6 −8
x= = = −4
2 2

24. On määritettävä funktion f(x) = x2 + 2x – 8 nollakohdat.
Eli ratkaistava yhtälö x2 + 2x – 8 = 0
ax2 + bx + c = 0
√
Toisen asteen yhtälö ratkaistaan ratkaisukaavalla: x =
−b ± b2 − 4ac
2a
2
x + 2x − 8 = 0
a=1 b=2 c = –8 Sijoitetaan kaavaan
−2 ±22 − 4 · 1 · (−8) 0
x=
2·1
√
−2 ± 4 + 32
=
2
=
−2 ± 6 x = –4 x=2
2
−2 + 6 4
x=
2
= =2
2
tai
−2 − 6 −8
x= = = −4
2 2