Downloaded 425 times
Uploaded byNida Nuzul Fitria
KONSEP JARAK TITIK, GARIS, DAN BIDANG PADA KUBUS
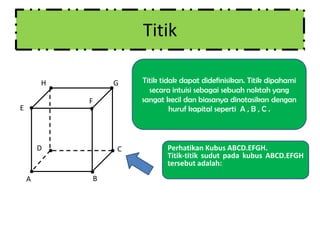
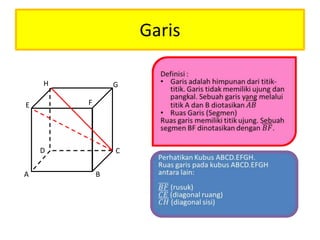
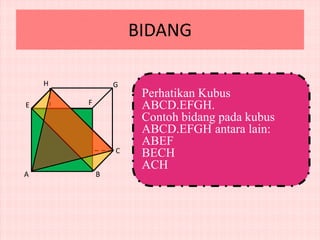
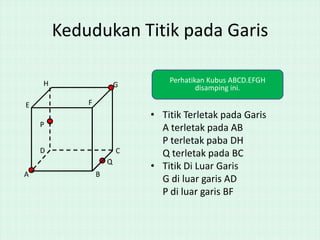
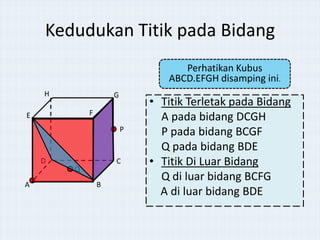
Dokumen ini membahas konsep jarak antara titik, garis, dan bidang pada kubus, dengan tujuan untuk membantu siswa kelas X memahami posisi dan hubungan antar elemen geometris tersebut. Melalui demonstrasi dan alat peraga, siswa diajarkan cara menentukan kedudukan titik pada garis dan bidang serta menghitung jarak antar elemen. Struktur dokumen juga mencakup soal-soal latihan untuk memperdalam pemahaman konsep yang diajarkan.
More Related Content
Similar to KONSEP JARAK TITIK, GARIS, DAN BIDANG PADA KUBUS
KONSEP JARAK TITIK, GARIS, DAN BIDANG PADA KUBUS
- 1. KONSEP JARAK TITIK,GARIS, DAN BIDANG PADA KUBUS SMA Kelas X Nida Nuzul Fitria 1002366 Pendidikan Matematika 2010
- 2. Kompetensi Dasar danIndikator Kompetensi Dasar 2.2 memahami konsep jarak dan sudut antara titik, garis dan bidang melalui demonstrasi menggunakan alat peraga atau media lainnya. Indikator • Menentukan kedudukan titik pada garis dan bidang • Menghitung jarak titik, garis, bidang pada kubus
- 3. Titik H G F E D A C B Titik tidak dapatdidefinisikan. Titik dipahami secara intuisi sebagai sebuah noktah yang sangat kecil dan biasanya dinotasikan dengan huruf kapital seperti A , B , C . Perhatikan Kubus ABCD.EFGH. Titik-titik sudut pada kubus ABCD.EFGH tersebut adalah:
- 4.
- 5.
- 6. BIDANG H G F E D A C B Perhatikan Kubus ABCD.EFGH. Contoh bidangpada kubus ABCD.EFGH antara lain: ABEF BECH ACH
- 7. DEFINISI • Jika suatutitik dilalui garis, maka dikatakan titik terletak pada garis tersebut. • Jika suatu titik tidak dilalui garis, maka dikatakan titik tersebut berada di luar garis. • Jika suatu titik dilewati suatu bidang, maka dikatakan titik itu terletak pada bidang. • Jika titik tidak dilewati suatu bidang, maka titik itu berada di luar bidang.
- 8. Kedudukan Titik padaGaris G Perhatikan Kubus ABCD.EFGH disamping ini. C H • Titik Terletak pada Garis A terletak pada AB P terletak paba DH Q terletak pada BC • Titik Di Luar Garis G di luar garis AD P di luar garis BF F E P D Q A B
- 9. Kedudukan Titik padaBidang Perhatikan Kubus ABCD.EFGH disamping ini. H G F E P D C Q A B • Titik Terletak pada Bidang A pada bidang DCGH P pada bidang BCGF Q pada bidang BDE • Titik Di Luar Bidang Q di luar bidang BCFG A di luar bidang BDE
- 10. Jarak Titik keGaris Perhatikan Kubus ABCD.EFGH dengan panjang rusuk 5 cm. H G F E Jarak titik A ke garis BF? 5 cm Q D A Caranyaa... P C 5 cm B Pertama, tarik garis dari titik A yang tegak lurus dengan garis BF Sehingga terlihat bahwa jarak dari titik A ke BF adalah 5 cm..
- 11. Jarak Antara DuaGaris yang Sejajar H G F E D A Perhatikan Kubus ABCD.EFGH dengan panjang rusuk 5 cm. C 5 cm B Berapakah jarak garis AH ke garis BG? Caranyaa.. 1. Tentukan salah satu titik pada AH, misalnya A.. 2. Tarik garis dari titik A yang tegak lurus dengan garis BG 3. Atau kita bisa menarik garis lain yang tegak lurus sepertii... 4. Atau.. 5. Sehingga jarak garis AH ke garis BG adalah 5 cm.
- 12. Jarak antara duabidang yang sejajar H G Perhatikan Kubus ABCD.EFGH dengan panjang rusuk 5 cm. F E Berapakah jarak dari bidang ADHE ke bidang BCGF? D A C 5 cm B Caranya.. 1. Tentukan salah satu titik pada bidang ADHE, misalnya A.. 2. Tarik garis dari titik A yang tegak lurus dengan bidang BCGF 3. Atau kita bisa menarik garis seperti ini.. 4. Sehingga jarak dari bidang ADHE ke bidang BCGH adalah 5 cm.
- 13. SOAL 1 Sebuah kardusberbentuk kubus ABCD.EFGH seperti gambar di bawah ini. Segmen atau ruas garis AB terletak pada garis g. a. Tentukan titik sudut kubus yang terletak pada garis g. b. Tentukan titik sudut kubus yang berada diHluar G garis g. F E D C g A B
- 14. JAWABAN SOAL 1 Pandangkubus ABCD.EFGH dan garis g dari gambar di atas, dapat diperoleh: a. Titik sudut kubus yang terletak pada garis g adalah titik A dan B, b. Titik sudut kubus yang berada di luar garis g adalah titik C, D, E, F, G, dan H.
- 15.
- 16.
- 17.