This document contains a project report on a fuzzy control system. It includes MATLAB code and results from several exercises involving fuzzy set operations on various membership functions defined over the interval [0,10]. Exercise 2.3 plots different membership functions and performs union and intersection operations on them. Exercise 2.4 calculates the α-cuts for each membership function. Exercise 2.5 plots a 3D membership function and its projections onto planes. Exercise 2.6 shows that a union of a set and its complement is not equal to the universal set. Exercise 2.8 states properties of convex fuzzy sets.

1. 1
PROJECT REPORT
ON
FUZZY CONTROL SYSTEM

2. 2
Index
Chapter: 2 …………………………………………………………………………………………
Exercise: 2.3 ……………………………………………………………………………
Exercise: 2.4 ……………………………………………………………………………
Exercise: 2.5 ……………………………………………………………………………
Exercise: 2.6 ……………………………………………………………………………
Exercise: 2.8 ……………………………………………………………………………

3. 3
Chapter: 2
Exercise: 2.3
𝜇 𝐹 =
𝑥
𝑥 + 2
, 𝑛𝑜𝑡 𝑧𝑒𝑟𝑜; 𝜇 𝐺 = 𝑒−𝑥 , 𝑎𝑏𝑜𝑢𝑡 𝑧𝑒𝑟𝑜; 𝜇 𝐻 =
1
1 + 10 (𝑥 − 2)2 , 𝑎𝑏𝑜𝑢𝑡 𝑡𝑤𝑜; 𝑥 𝜖 [0,10]
close all; clc; clear all; syms x
muF=x/(x+2);muG=exp(-x);muH=1/(1+10*(x-2)^2);
xx=0:0.1:10;
figure
plot(xx,subs(muF,x,xx),xx,subs(muG,x,xx),xx,subs(muH,x,xx))
legend('mu_F(x)','mu_G(x)','mu_H(x)')
𝜇 𝐹̅ = 1 −
𝑥
𝑥 + 2
; 𝜇 𝐺̅ = 1 − 𝑒−𝑥 ; 𝜇 𝐻̅ = 1 −
1
1 + 10 (𝑥 − 2)2 ; 𝑥 𝜖 [0,10]
figure
plot(xx,subs(1-muF,x,xx),xx,subs(1-muG,x,xx),xx,subs(1-muH,x,xx))
legend('1-mu_F(x)','1-mu_G(x)','1-mu_H(x)')

4. 4
𝜇 𝐹∪𝐺 = max
𝑥∈[0,10]
{ 𝜇 𝐹 , 𝜇 𝐺 } = max
𝑥∈[0,10]
{
𝑥
𝑥 + 2
, 𝑒−𝑥}
𝜇 𝐹∪𝐻 = max
𝑥∈[0,10]
{ 𝜇 𝐹 , 𝜇 𝐻 } = max
𝑥∈[0,10]
{
𝑥
𝑥 + 2
,
1
1 + 10 (𝑥 − 2)2}
𝜇 𝐺∪𝐻 = max
𝑥∈[0,10]
{ 𝜇 𝐺 , 𝜇 𝐻 } = max
𝑥∈[0,10]
{ 𝑒−𝑥 ,
1
1 + 10 (𝑥 − 2)2}
FUG=max(subs(muF,x,xx),subs(muG,x,xx));
FUH=max(subs(muF,x,xx),subs(muH,x,xx));
GUH=max(subs(muG,x,xx),subs(muH,x,xx));
figure
plot(xx,FUG,xx,FUH,xx,GUH)
legend('FUG','FUH','GUH')

5. 5
𝜇 𝐹∩𝐺 = min
𝑥∈[0,10]
{ 𝜇 𝐹 , 𝜇 𝐺 } = min
𝑥∈[0,10]
{
𝑥
𝑥 + 2
, 𝑒−𝑥}
𝜇 𝐹∩𝐻 = min
𝑥∈[0,10]
{ 𝜇 𝐹 , 𝜇 𝐻 } = min
𝑥∈[0,10]
{
𝑥
𝑥 + 2
,
1
1 + 10 (𝑥 − 2)2}
𝜇 𝐺∩𝐻 = min
𝑥∈[0,10]
{ 𝜇 𝐺 , 𝜇 𝐻 } = min
𝑥∈[0,10]
{ 𝑒−𝑥 ,
1
1 + 10 (𝑥 − 2)2}
FUG=max(subs(muF,x,xx),subs(muG,x,xx));
FUH=max(subs(muF,x,xx),subs(muH,x,xx));
GUH=max(subs(muG,x,xx),subs(muH,x,xx));
figure
plot(xx,FUG,xx,FUH,xx,GUH)
legend('FUG','FUH','GUH')

6. 6
𝜇 𝐹∪𝐺∪𝐻 = max
𝑥∈[0,10]
{ 𝜇 𝐹 , 𝜇 𝐺 , 𝜇 𝐻 } = max
𝑥∈[0,10]
{
𝑥
𝑥 + 2
, 𝑒−𝑥,
1
1 + 10 (𝑥 − 2)2}
𝜇 𝐹∩𝐺∩𝐻 = min
𝑥∈[0,10]
{ 𝜇 𝐹 , 𝜇 𝐺 , 𝜇 𝐻 } = min
𝑥∈[0,10]
{
𝑥
𝑥 + 2
, 𝑒−𝑥,
1
1 + 10 (𝑥 − 2)2}
FUGUH=max(subs(muF,x,xx),GUH);
FandGandH=min(subs(muF,x,xx),GandH);
figure
plot(xx,FUGUH,xx,FandGandH)
legend('FcupGcupH','FcapHcapG')

7. 7
𝜇 𝐹∩𝐻̅ = min
𝑥∈[0,10]
{ 𝜇 𝐹 ,1 − 𝜇 𝐻 } = min
𝑥∈[0,10]
{
𝑥
𝑥 + 2
,1 −
1
1 + 10 (𝑥 − 2)2}
𝜇 𝐺∪𝐻̅ = max
𝑥∈[0,10]
{ 𝜇 𝐺 ,1 − 𝜇 𝐻 } = max
𝑥∈[0,10]
{ 𝑒−𝑥 ,1 −
1
1 + 10 (𝑥 − 2)2}
𝜇 𝐹̅∩𝐻̅ = min
𝑥∈[0,10]
{1 − 𝜇 𝐹 ,1 − 𝜇 𝐻 } = min
𝑥∈[0,10]
{1 −
𝑥
𝑥 + 2
, 1 −
1
1 + 10 (𝑥 − 2)2}
FandbarH=min(subs(muF,x,xx),1-subs(muH,x,xx));
GUbarH=max(subs(muG,x,xx),1-subs(muH,x,xx));
barFandbarH=min(1-subs(muF,x,xx),1-subs(muH,x,xx));
figure
plot(xx,FandbarH,xx,GUbarH,xx,barFandbarH)
legend('Fcap(1-H)','Gcup(1-H)','(1-F)cap(1-H)')

8. 8
Exercise: 2.4
𝜇 𝐹 =
𝑥
𝑥 + 2
, 𝑛𝑜𝑡 𝑧𝑒𝑟𝑜; 𝜇 𝐺 = 𝑒−𝑥 , 𝑎𝑏𝑜𝑢𝑡 𝑧𝑒𝑟𝑜; 𝜇 𝐻 =
1
1 + 10 (𝑥 − 2)2 , 𝑎𝑏𝑜𝑢𝑡 𝑡𝑤𝑜; 𝑥 𝜖 [0,10]
𝐹𝑎 = { 𝑥 ∈ 𝑈| 𝜇 𝐹 ≥ 𝑎} = {𝑥 ∈ 𝑈
𝑥
𝑥 + 2
≥ 𝑎} , 𝑈 = [0,10]
𝑥
𝑥 + 2
≥ 𝑎 ⇒
2𝑎
1 − 𝑎
≤ 𝑥 ≤ 10 ⇒ 𝐹𝑎 = [
2𝑎
1 − 𝑎
, 10]
𝐺𝑎 = { 𝑥 ∈ 𝑈| 𝜇 𝐺 ≥ 𝑎} = { 𝑥 ∈ 𝑈| 𝑒−𝑥 ≥ 𝑎}, 𝑈 = [0,10]
1 ≥ 𝑒−𝑥 ≥ 𝑎 ⇒ 0 ≤ 𝑥 ≤ −In( 𝑎) ⇒ 𝐺𝑎 = [0, In( 𝑎)]
𝐻 𝑎 = { 𝑥 ∈ 𝑈| 𝜇 𝐻 ≥ 𝑎} = { 𝑥 ∈ 𝑈 |
𝑥
1 + 10 (𝑥 − 2)2 ≥ 𝑎} , 𝑈 = [0,10]
1
1 + 10 (𝑥 − 2)2 ≥ 𝑎 ⇒ 2 − √
1
𝑎
− 1
10
≤ 𝑥 ≤ 2 + √
1
𝑎
− 1
10
⇒ 𝐻 𝑎 = [2√
1
𝑎
− 1
10
,2 + √
1
𝑎
− 1
10
]
𝑎 𝐹𝑎 𝐺𝑎 𝐻 𝑎
0.2 [0.5,10] [0,−In(0.2)] [2 − √
2
5
,2 + √
2
5
]
0.5 [2,10] [0,−In(0.5)] [2 − √
1
10
,2 + √
1
10
]

9. 9
0.9 ∅ [0, −In(0.9)] [2 − √
1
90
,2 + √
1
90
]
1 ∅ [0,0] 2
−[ln(0.2), ln(0.5), ln(0.9), ln(1)] = [1.6094 0.6931 0.1054 0]
close all; clc; clear all; syms x
muF=x/(x+2);muG=exp(-x);muH=1/(1+10*(x-2)^2);
xx=0:0.1:10;
Falpha= subs(muF,x,xx)
figure
plot(xx,subs(muF,x,xx),xx,subs(muG,x,xx),xx,subs(muH,x,xx),xx,alpha*(ones(size(xx)
legend('mu_F(x)','mu_G(x)','mu_H(x)')
-[log(alpha1),log(alpha2),log(alpha3),log(alpha4)]
Exercise: 2.5
𝜇 𝐴( 𝑥1,𝑥2) = 𝑒−(𝑥1
2+𝑥2
2);𝑈 = [−1,1] × [−3,3]
𝐻1 = { 𝑥 𝜖 𝑈| 𝑥1 = 0}, 𝐻2 = { 𝑥 𝜖 𝑈| 𝑥2 = 0}
𝜇 𝐴𝐻1
( 𝑥2) = sup
𝑥1∈[−1,1]
𝜇 𝐴( 𝑥1, 𝑥2) = sup
𝑥1∈[−1,1]
𝑒−(𝑥1
2+𝑥2
2) = 𝑒−𝑥2
2

10. 10
𝜇 𝐴𝐻2
( 𝑥1) = sup
𝑥2∈[−3,3]
𝜇 𝐴( 𝑥1,𝑥2) = sup
𝑥2∈[−3,3]
𝑒−(𝑥1
2+𝑥2
2) = 𝑒−𝑥1
2
close all; clc; clear all;
x1=-1:0.01:1;x2=-3:0.03:3;[x,y]=meshgrid(x1,x2);
muA=exp(-(x.^2+y.^2));
figure
mesh(x,y,muA)
xlabel('x_1');ylabel('x_2');zlabel('e^{-(x_1^2+x_2^2)}')
x1=-1:0.01:1;x2=-3:0.03:3;[x,y]=meshgrid(x1,x2);
muAH1=exp(-(y.^2));
figure
mesh(x,y,muAH1)
xlabel('x_1');ylabel('x_2');zlabel('e^{-(x_2^2)}')
x1=-1:0.01:1;x2=-3:0.03:3;[x,y]=meshgrid(x1,x2);
muAH2=exp(-(x.^2));
figure
mesh(x,y,muAH2)
xlabel('x_1');ylabel('x_2');zlabel('e^{-(x_1^2)}')

11. 11
Exercise: 2.6
𝜇 𝐹( 𝑥) = 𝑥; 𝜇 𝐹̅( 𝑥) = 1 − 𝑥
⇒ 𝜇 𝐹∪𝐹̅( 𝑥) = max
𝑥∈[0,1]
{𝜇 𝐹( 𝑥), 𝜇 𝐹̅( 𝑥)} = | 𝑥 − 0.5| + 0.5 ≠ 1 = 𝜇 𝑈( 𝑥) = 1, ∀𝑥 ∈ [0,1]
close all; clc; clear all;
x=0:0.01:1; muF=x;mubarF=1-x;FUbarF=max(muF,mubarF);
figure
plot(x,muF,x,mubarF)
legend('mu_F','1-mu_F')
figure
plot(x,FUbarF,x,ones(1,size(x,2)))
legend('mu_Fcup(1-mu_F)','mu_U=1','Location','SouthEast')
axis([0,1,0,1])

12. 12
Exercise: 2.8
𝜇 𝐴( 𝑥) = 𝑥; 𝜇 𝐵( 𝑥) = 1 − 𝑥, 𝑥 ∈ 𝑈 = [0,1];
⇒ 𝜇 𝐴∪𝐵( 𝑥) = max
𝑥∈[0,1]
{𝜇 𝐴( 𝑥), 𝜇 𝐵( 𝑥)} = | 𝑥 − 0.5| + 0.5
⇒ 𝜇 𝐴∩𝐵( 𝑥) = min
𝑥∈[0,1]
{𝜇 𝐴( 𝑥), 𝜇 𝐵( 𝑥)} = 0.5 − | 𝑥 − 0.5|
𝜇 𝐴( 𝜆𝑥1 + (1 − 𝜆) 𝑥2) ≥ min{𝜇 𝐴( 𝑥1), 𝜇 𝐴( 𝑥2)}
𝜇 𝐴( 𝜆𝑥1 + (1 − 𝜆) 𝑥2) ≥ min{𝜇 𝐵( 𝑥1),𝜇 𝐵( 𝑥2)}
𝜇 𝐴∩𝐵( 𝜆𝑥1 + (1 − 𝜆) 𝑥2) = min{𝜇 𝐴( 𝜆𝑥1 + (1 − 𝜆) 𝑥2), 𝜇 𝐵( 𝜆𝑥1 + (1 − 𝜆) 𝑥2)}
≥ min{min{ 𝜇 𝐴( 𝑥1), 𝜇 𝐴(𝑥2)},min{min{ 𝜇 𝐵( 𝑥1), 𝜇 𝐵(𝑥2)}}
≥ min{min{ 𝜇 𝐴( 𝑥1), 𝜇 𝐵(𝑥1)},min{min{ 𝜇 𝐴( 𝑥2), 𝜇 𝐵(𝑥2)}}
= min{𝜇 𝐴⋂𝐵( 𝑥1),𝜇 𝐴⋂𝐵( 𝑥2)}
𝜇 𝐴∪𝐵( 𝜆𝑥1 + (1 − 𝜆) 𝑥2) = max{𝜇 𝐴( 𝜆𝑥1 + (1 − 𝜆) 𝑥2), 𝜇 𝐵( 𝜆𝑥1 + (1 − 𝜆) 𝑥2)}
= 𝑚𝑎𝑥 {min{𝜇 𝐴( 𝑥1),𝜇 𝐴(𝑥2)},min{min{ 𝜇 𝐵( 𝑥1), 𝜇 𝐵(𝑥2)}}
= max{min{ 𝜇 𝐴( 𝑥1),𝜇 𝐵(𝑥1)},min{min{ 𝜇 𝐴( 𝑥2), 𝜇 𝐵(𝑥2)}}
≠ min{ max { 𝜇 𝐴( 𝑥1), 𝜇 𝐵(𝑥1)},min{min{ 𝜇 𝐴( 𝑥2),𝜇 𝐵(𝑥2)}}
= min{𝜇 𝐴∪𝐵( 𝑥1), 𝜇 𝐴∪𝐵( 𝑥2)}
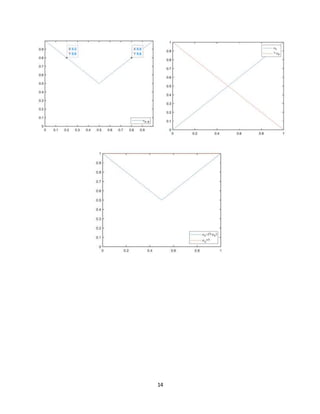
𝑥1 = 0.2, 𝑥2 = 0.8 ⇒ 𝜇 𝐴∪𝐵(0.2) = 𝜇 𝐴∪𝐵(0.8) = 0.8 = min{𝜇 𝐴∪𝐵(0.2), 𝜇 𝐴∪𝐵(0.8)}
𝜇 𝐴∪𝐵(0.2𝜆 + (1 − 𝜆)0.8) ≤ 0.8 = min{𝜇 𝐴∪𝐵(0.2), 𝜇 𝐴∪𝐵(0.8)}
𝜆 = 0.5 ⇒ 𝜇 𝐴∪𝐵(0.5) = 0.5 < 0.8 = min{𝜇 𝐴∪𝐵(0.2), 𝜇 𝐴∪𝐵(0.8)}
𝜇 𝐴∪𝐵 is not convex

13. 13
close all; clc; clear all;
x=0:0.01:1; muA=x;muB=1-x;AUB=max(muA,muB);AandB=min(muA,muB);
figure
plot(x,muA,x,muB)
legend('mu_A','mu_B')
figure
plot(x,AandB)
legend('mu_{AcapB}')
axis([0,1,0,1])
figure
plot(x,AUB)
legend('mu_{AcupB}','Location','SouthEast')
axis([0,1,0,1])

14. 14