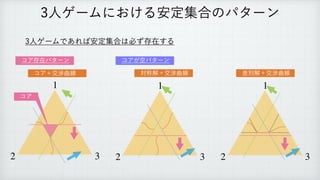
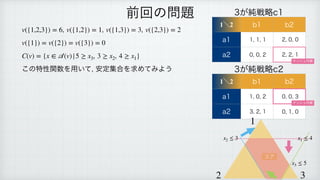
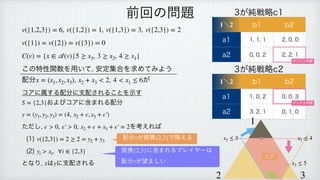
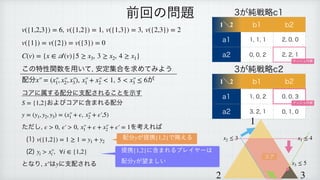
1) The document defines a set function v and a set C(v) for a set A(v). 2) It provides two examples where it constructs a vector y that dominates a given vector x according to the definitions. 3) The examples illustrate the concept of finding a dominating vector y for a given vector x based on the set function and conditions defined.

1. ήʔϜཧ࿦#4*$ԋश
҆ఆू߹Λ‫ٻ‬ΊΔ

2. ҆ఆू߹ͷఆٛͷ֬ೝ
ίΞͱ҆ఆू߹
ਓήʔϜʹ͓͚Δ҆ఆू߹ͷύλʔϯ
લճͷ໰୊

3. ҆ఆू߹ͷఆٛͷ֬ೝ
ఆٛɿ഑෼ͷࢧ഑
̎ͭͷ഑෼ ͱఏ‫ܞ‬ ΛͱΔ࣍ͷ̎৚͕݅ຬͨ͞ΕΔͱ͖
͸ Λ Λ௨ͯ͠ࢧ഑͢Δͱ͍͍
ͱॻ͘
̎ͭͷ഑෼ ʹରͯ͠
͋Δఏ‫ܞ‬ ͕ଘࡏͯ͠ ͕੒Γཱͭͱ͖
୯ʹ ͸ Λࢧ഑͢Δͱ͍͍
ͱॻ͘
x, y S ⊆ N
x y S x domS y
v(S) ≥
∑
i∈S
xi
xi yi, ∀i ∈ S
x, y S x domS y
x y x dom y
഑෼ ͕ఏ‫ܞ‬ Ͱ࿫͑Δ
x S
ఏ‫ܞ‬ ʹ‫·ؚ‬ΕΔϓϨΠϠʔʹͱͬͯ
഑෼ ͕ΑΓ๬·͍͠
S
x

4. ҆ఆू߹ͷఆٛͷ֬ೝ
ఆٛ
ಛੑؔ਺‫ܗ‬ήʔϜ ʹ͓͍ͯ
഑෼ͷू߹ ͕҆ఆू߹Ͱ͋Δͱ͸
ҎԼΛຬͨ͢ͱ͖Λ͍͏
֎෦҆ఆੑ
ʹଐ͞ͳ͍͢΂ͯͷ഑෼ ʹؔͯ͠
͋Δ ಺ͷ഑෼ ͕ଘࡏͯ͠
͕ Λࢧ഑͢Δ
಺෦҆ఆੑ
಺ͷ೚ҙͷ഑෼ ʹ͍ͭͯ‫ʹ͍ޓ‬ଞΛࢧ഑͠ͳ͍
ิ
ίΞ͸഑෼ʹରͯ͠ఆ͕ٛͨ͠
҆ఆू߹͸഑෼ͷ෦෼ू߹ʹରͯ͠ఆٛ͢Δ
ิ
ϑΥϯϊΠϚϯϞϧήϯγϡςϧϯղͱ΋‫ݺ‬͹ΕΔ
(N, v) K
K y
K x x y
K x, y

5. ίΞͱ҆ఆू߹
ఆཧ
ಛੑؔ਺‫ܗ‬ήʔϜ ʹ͓͍ͯ
ίΞͱ҆ఆू߹͕‫ʹڞ‬ଘࡏ͢ΔͳΒ͹
ίΞ͸҆ఆू߹ʹ‫·ؚ‬ΕΔ
Λࣔͤ͹Α͍
೚ҙͷ ΛͱΔ͜ͷͱ͖ Ͱ͋Δ͜ͱΛࣔͤ͹Α͍
ͱ͢Δͱ
͸͋Δ഑෼ ʹࢧ഑͞ΕΔ͜ͱʹͳΔͨΊ
͕ίΞͷ഑෼Ͱ͋Δ͜ͱʹໃ६
(N, v)
C(v) ⊆ K
x ∈ C(v) x ∈ K
x ∉ K x x′

∈ K
x ֎෦҆ఆੑ
ʹଐ͞ͳ͍͢΂ͯͷ഑෼ ʹؔͯ͠
͋Δ ಺ͷ഑෼ ͕ଘࡏͯ͠
͕ Λࢧ഑͢Δ
K y
K x x y

6. ਓήʔϜʹ͓͚Δ҆ఆू߹ͷύλʔϯ
ਓήʔϜͰ͋Ε͹҆ఆू߹͸ඞͣଘࡏ͢Δ
1
2 3
ίΞ
1
2 3
ίΞଘࡏύλʔϯ ίΞ͕ۭύλʔϯ
1
2 3
ରশղʴަব‫ۂ‬ઢ ࠩผղʴަব‫ۂ‬ઢ
ίΞʴަব‫ۂ‬ઢ

7.
͜ͷಛੑؔ਺Λ༻͍ͯ
҆ఆू߹Λ‫ٻ‬ΊͯΈΑ͏
v({1,2,3}) = 6 v({1,2}) = 1 v({1,3}) = 3 v({2,3}) = 2
v({1}) = v({2}) = v({3}) = 0
C(v) = {x ∈
𝒜
(v)|5 ≥ x3, 3 ≥ x2, 4 ≥ x1}
લճͷ໰୊ ͕७ઓུD
1ʘ2 C C
B
B
͕७ઓུD
1ʘ2 C C
B
B
φογϡ‫ߧۉ‬
φογϡ‫ߧۉ‬
1
2 3
x1 ≤ 4
x2 ≤ 3
x3 ≤ 5
ίΞ

8.
͜ͷಛੑؔ਺Λ༻͍ͯ
҆ఆू߹Λ‫ٻ‬ΊͯΈΑ͏
ਓήʔϜͳͷͰ҆ఆू߹͸ඞͣଘࡏ͠
͔ͭ͜ͷήʔϜ͸ίΞ͕ଘࡏ͢Δ
ίΞʹଐ͢Δ഑෼͸͢΂ͯ
҆ఆू߹ʢ഑෼ͷू߹ʣʹ‫·ؚ‬ΕΔ
v({1,2,3}) = 6 v({1,2}) = 1 v({1,3}) = 3 v({2,3}) = 2
v({1}) = v({2}) = v({3}) = 0
C(v) = {x ∈
𝒜
(v)|5 ≥ x3, 3 ≥ x2, 4 ≥ x1}
લճͷ໰୊ ͕७ઓུD
1ʘ2 C C
B
B
͕७ઓུD
1ʘ2 C C
B
B
φογϡ‫ߧۉ‬
φογϡ‫ߧۉ‬
1
2 3
x1 ≤ 4
x2 ≤ 3
x3 ≤ 5
ίΞ

9.
͜ͷಛੑؔ਺Λ༻͍ͯ
҆ఆू߹Λ‫ٻ‬ΊͯΈΑ͏
഑෼
͕
ίΞʹଐ͢Δ഑෼ʹࢧ഑͞ΕΔ͜ͱΛࣔ͢
͓ΑͼίΞʹ‫·ؚ‬ΕΔ഑෼
ͨͩ͠
Λߟ͑Ε͹
ͱͳΓ
͸ ʹࢧ഑͞ΕΔ
v({1,2,3}) = 6 v({1,2}) = 1 v({1,3}) = 3 v({2,3}) = 2
v({1}) = v({2}) = v({3}) = 0
C(v) = {x ∈
𝒜
(v)|5 ≥ x3, 3 ≥ x2, 4 ≥ x1}
x = (x1, x2, x3), x2 + x3 2 4 x1 ≤ 6
S = {2,3}
y = (y1, y2, y3) = (4, x2 + ϵ, x3 + ϵ′

)
ϵ 0, ϵ′

0, x2 + ϵ + x3 + ϵ′

= 2
v({2,3}) = 2 ≥ 2 = y2 + y3
yi xi, ∀i ∈ {2,3}
x y
લճͷ໰୊ ͕७ઓུD
1ʘ2 C C
B
B
͕७ઓུD
1ʘ2 C C
B
B
φογϡ‫ߧۉ‬
φογϡ‫ߧۉ‬
1
2 3
x1 ≤ 4
x2 ≤ 3
x3 ≤ 5
ίΞ
഑෼ ͕ఏ‫ܞ‬ Ͱ࿫͑Δ
y {2,3}
ఏ‫ܞ‬ ʹ‫·ؚ‬ΕΔϓϨΠϠʔ͸
഑෼ ͕๬·͍͠
{2,3}
y

10.
͜ͷಛੑؔ਺Λ༻͍ͯ
҆ఆू߹Λ‫ٻ‬ΊͯΈΑ͏
഑෼
͕
ίΞʹଐ͢Δ഑෼ʹࢧ഑͞ΕΔ͜ͱΛࣔ͢
͓ΑͼίΞʹ‫·ؚ‬ΕΔ഑෼
ͨͩ͠
Λߟ͑Ε͹
ͱͳΓ
͸ ʹࢧ഑͞ΕΔ
v({1,2,3}) = 6 v({1,2}) = 1 v({1,3}) = 3 v({2,3}) = 2
v({1}) = v({2}) = v({3}) = 0
C(v) = {x ∈
𝒜
(v)|5 ≥ x3, 3 ≥ x2, 4 ≥ x1}
x′

= (x′

1, x′

2, x′

3), x′

1 + x′

3 3 3 x′

2 ≤ 6
S = {1,3}
y = (y1, y2, y3) = (x′

1 + ϵ, 3, x′

3 + ϵ′

)
ϵ 0, ϵ′

0, x′

1 + ϵ + x′

3 + ϵ′

= 3
v({1,3}) = 3 ≥ 3 = y1 + y3
yi x′

i, ∀i ∈ {1,3}
x′

y
લճͷ໰୊ ͕७ઓུD
1ʘ2 C C
B
B
͕७ઓུD
1ʘ2 C C
B
B
φογϡ‫ߧۉ‬
φογϡ‫ߧۉ‬
1
2 3
x1 ≤ 4
x2 ≤ 3
x3 ≤ 5
ίΞ
഑෼ ͕ఏ‫ܞ‬ Ͱ࿫͑Δ
y {1,3}
ఏ‫ܞ‬ ʹ‫·ؚ‬ΕΔϓϨΠϠʔ͸
഑෼ ͕๬·͍͠
{1,3}
y

11.
͜ͷಛੑؔ਺Λ༻͍ͯ
҆ఆू߹Λ‫ٻ‬ΊͯΈΑ͏
഑෼
͕
ίΞʹଐ͢Δ഑෼ʹࢧ഑͞ΕΔ͜ͱΛࣔ͢
͓ΑͼίΞʹ‫·ؚ‬ΕΔ഑෼
ͨͩ͠
Λߟ͑Ε͹
ͱͳΓ
͸ ʹࢧ഑͞ΕΔ
v({1,2,3}) = 6 v({1,2}) = 1 v({1,3}) = 3 v({2,3}) = 2
v({1}) = v({2}) = v({3}) = 0
C(v) = {x ∈
𝒜
(v)|5 ≥ x3, 3 ≥ x2, 4 ≥ x1}
x′

′

= (x′

′

1, x′

′

2, x′

′

3), x′

′

1 + x′

′

2 1 5 x′

′

3 ≤ 6
S = {1,2}
y = (y1, y2, y3) = (x′

′

1 + ϵ, x′

′

2 + ϵ′

,5)
ϵ 0, ϵ′

0, x′

′

1 + ϵ + x′

′

2 + ϵ′

= 1
v({1,2}) = 1 ≥ 1 = y1 + y2
yi x′

′

i , ∀i ∈ {1,2}
x′

′

y
લճͷ໰୊ ͕७ઓུD
1ʘ2 C C
B
B
͕७ઓུD
1ʘ2 C C
B
B
φογϡ‫ߧۉ‬
φογϡ‫ߧۉ‬
1
2 3
x1 ≤ 4
x2 ≤ 3
x3 ≤ 5
ίΞ
഑෼ ͕ఏ‫ܞ‬ Ͱ࿫͑Δ
y {1,2}
ఏ‫ܞ‬ ʹ‫·ؚ‬ΕΔϓϨΠϠʔ͸
഑෼ ͕๬·͍͠
{1,2}
y

12.
͜ͷಛੑؔ਺Λ༻͍ͯ
҆ఆू߹Λ‫ٻ‬ΊͯΈΑ͏
Ҏ্ͷٞ࿦ΑΓ
҆ఆू߹͸ίΞʹ‫·ؚ‬ΕΔ഑෼ͷू߹
v({1,2,3}) = 6 v({1,2}) = 1 v({1,3}) = 3 v({2,3}) = 2
v({1}) = v({2}) = v({3}) = 0
C(v) = {x ∈
𝒜
(v)|5 ≥ x3, 3 ≥ x2, 4 ≥ x1}
લճͷ໰୊ ͕७ઓུD
1ʘ2 C C
B
B
͕७ઓུD
1ʘ2 C C
B
B
φογϡ‫ߧۉ‬
φογϡ‫ߧۉ‬
1
2 3
x1 ≤ 4
x2 ≤ 3
x3 ≤ 5
ίΞ
҆ఆू߹

13. ήʔϜཧ࿦#4*$ԋश
҆ఆू߹Λ‫ٻ‬ΊΔ
࣍ճɿԋश