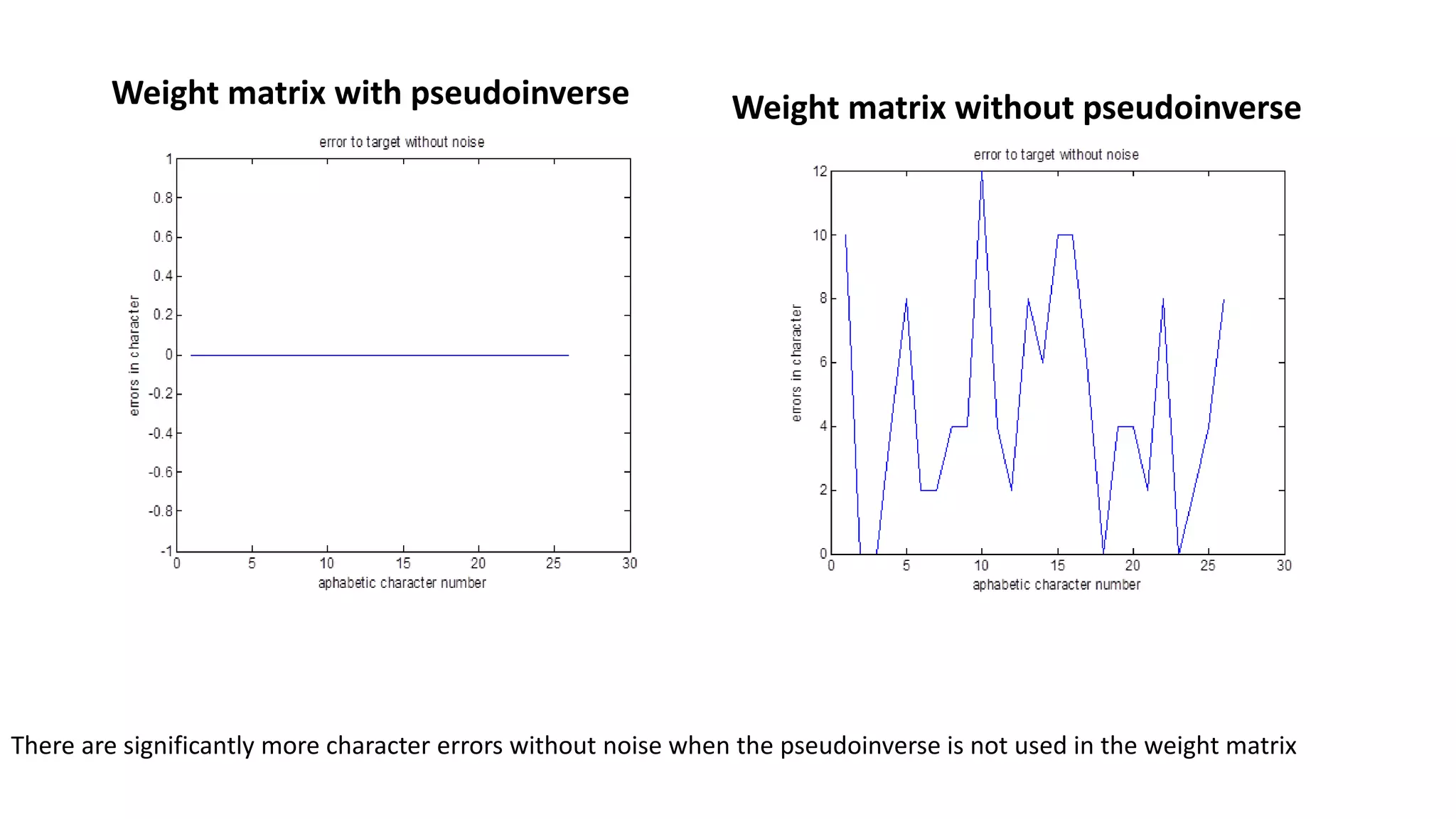
The document discusses autoassociative memory performance with and without using a pseudoinverse weight matrix. It finds that using a pseudoinverse weight matrix limits the range of values in the matrix and improves performance both without noise and with noise present. Specifically, it finds that without a pseudoinverse, there are significantly more character errors without noise and the autoassociative memory has much better performance in dealing with noise when a pseudoinverse is used to calculate the weight matrix.

1. Autoassociative Memory
performance with and without
pseudoinverse weight matrix
Submitted by:- Submitted to:-
Bhupender Singh (151602) Dr. Kanika Sharma
NITTTR, Chandigarh

2. Introduction
A content-addressable memory is a type
of memory that allows for the recall of
data based on the degree of similarity
between the input pattern and the
patterns stored in memory
memory is robust and fault-tolerant
auto associative
 hetero associative

3.  An auto associative memory is used to retrieve a previously stored
pattern that most closely resembles the current pattern
In auto associative memory y[1],y[2],y[3],…….y[m] number of stored
pattern and an output pattern vector y[m] can be obtained from noisy
y[m]
Hetero associative memory:- the retrieved pattern is, in general,
different from the input pattern not only in content but possibly also
different in type and format.
in hetero associative memory {c(1),y(1)},{c(2),y(2)},…….{( 𝑐m,ym)}
output a pattern vector y(m) if noisy or incomplete version of c(m) is
input.

4. Applications:-
 Image segmentation
 Face detection
 Computer graphics ,multimedia and multifractal analysis.
 Signature detection
 Image recognition

5. The problem is divided into 5 sections
1) generating the alphabetical
target vectors
2) calculating the weight matrix
W with the pseudoinverse
3) testing the auto associative
memory without noise,
4) testing the auto associative
memory with noise
 5) comparing to the results
without using the pseudoinverse

6. Encoding or memoriization :-
An associative memory can be form by constructing a weight matrix W
connection. Weight matrix value of correlation matrix are computed as
(𝑊𝑖𝑗) 𝑘= (𝑥𝑖) 𝑘 (𝑦𝑗) 𝑘
(𝑥𝑖) 𝑘 is ith component of Xk path and (𝑦𝑗) 𝑘is jth component of pattern (𝑦) 𝑘
W=∝ 𝑘=1
𝑝
𝑤 𝑘
∝ is proportionality constant or normalizing constan
W= 𝑇 ∗ 𝑇 𝑇
• The output of the function a=hard lim (W*𝑡 𝑛𝑜𝑖𝑠𝑒)

7. Retrieval or recalling:-
The process of retrieval of stored pattern is called decoding.
𝑌𝑖𝑛𝑗= 𝑖=1
𝑛
𝑥𝑖 𝑤𝑖𝑗
 Apply the following activation function to calculate the output
𝑌𝑗 = 𝑓 𝑌𝑖𝑛𝑗 =
−1 𝑖𝑓 𝑌𝑖𝑛𝑗 > 0
+1 𝑖𝑓 𝑌𝑖𝑛𝑗 < 0
To minimize the error the pseudoinverse of the target matrix T to
minimize the cross correlation between input vectors t.
• W=T*𝑇+

8. RESULT and DISCUSSION(Performance with
and without pseudoinverse weight matrix:-):-
Weight matrix with pseudoinverse Weight matrix without pseudoinverse
Using the pseudoinverse in limits the range of the weight matrix from 0 to 1. Not using the pseudoinverse results in a larger
range of values –20 to 25. The off diagonal elements have a lot higher values. This indicates cross correlation

9. Weight matrix with pseudoinverse Weight matrix without pseudoinverse
There are significantly more character errors without noise when the pseudoinverse is not used in the weight matrix

10. Weight matrix with pseudoinverse Weight matrix without pseudoinverse
autoassociative memory using the pseudoinverse has much improved performance in noise which follows from the
performance without noise.

11. Conclusion:-
 There are significantly more character errors without noise when the
pseudoinverse is not used in the weight matrix
Using the pseudoinverse in limits the range of the weight matrix
from 0 to 1. Not using the pseudoinverse results in a larger range of
values –20 to 25. The off diagonal elements have a lot higher values.
This indicates cross correlation
Auto associative memory using the pseudoinverse has much
improved performance in noise which follows from the performance
without noise.

12. References:-
[1] J. A. Anderson, “A simple neural network generating an interactive
memory,” Mathematical Biosciences, vol. 14, no. 3-4, pp. 197–220, 1972.
[2] T. Kohonen, “Correlation matrix memories,” IEEE Trans. Comput., vol.
C-21, no. 4, pp. 353–359, 1972.
[3] K. Nakano, “Associatron–a model of associative memory,” IEEE Trans.
Syst., Man, Cybern., vol. 2, no. 3, pp. 380–388, 1972.
[4] J. J. Hopfield, “Neural networks and physical systems with emergent
collective computational abilities,” Proc. Natl. Acad. Sci. USA, vol. 79,
no. 8, pp. 2554–2558, 1982.

13. Thanks