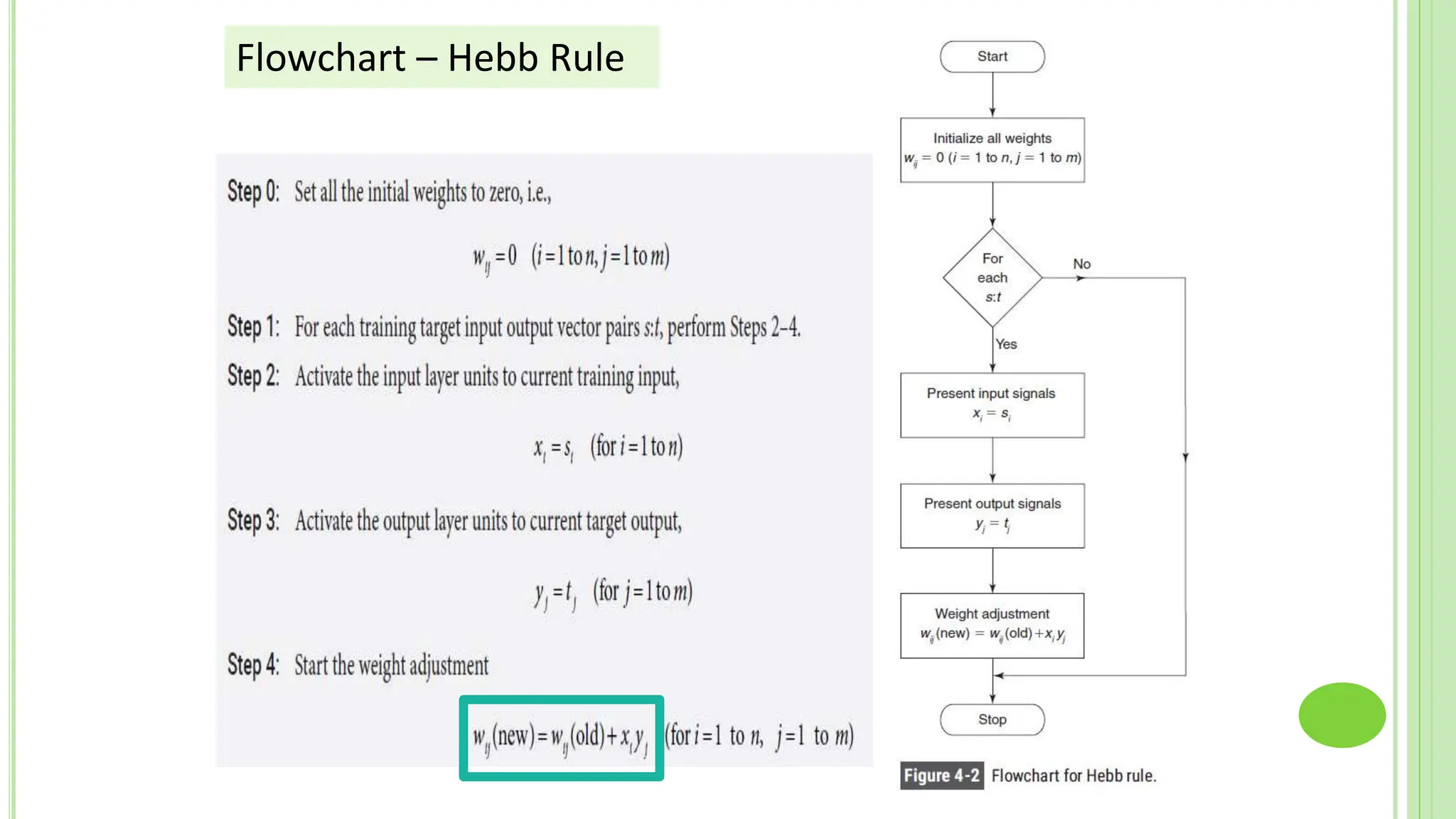
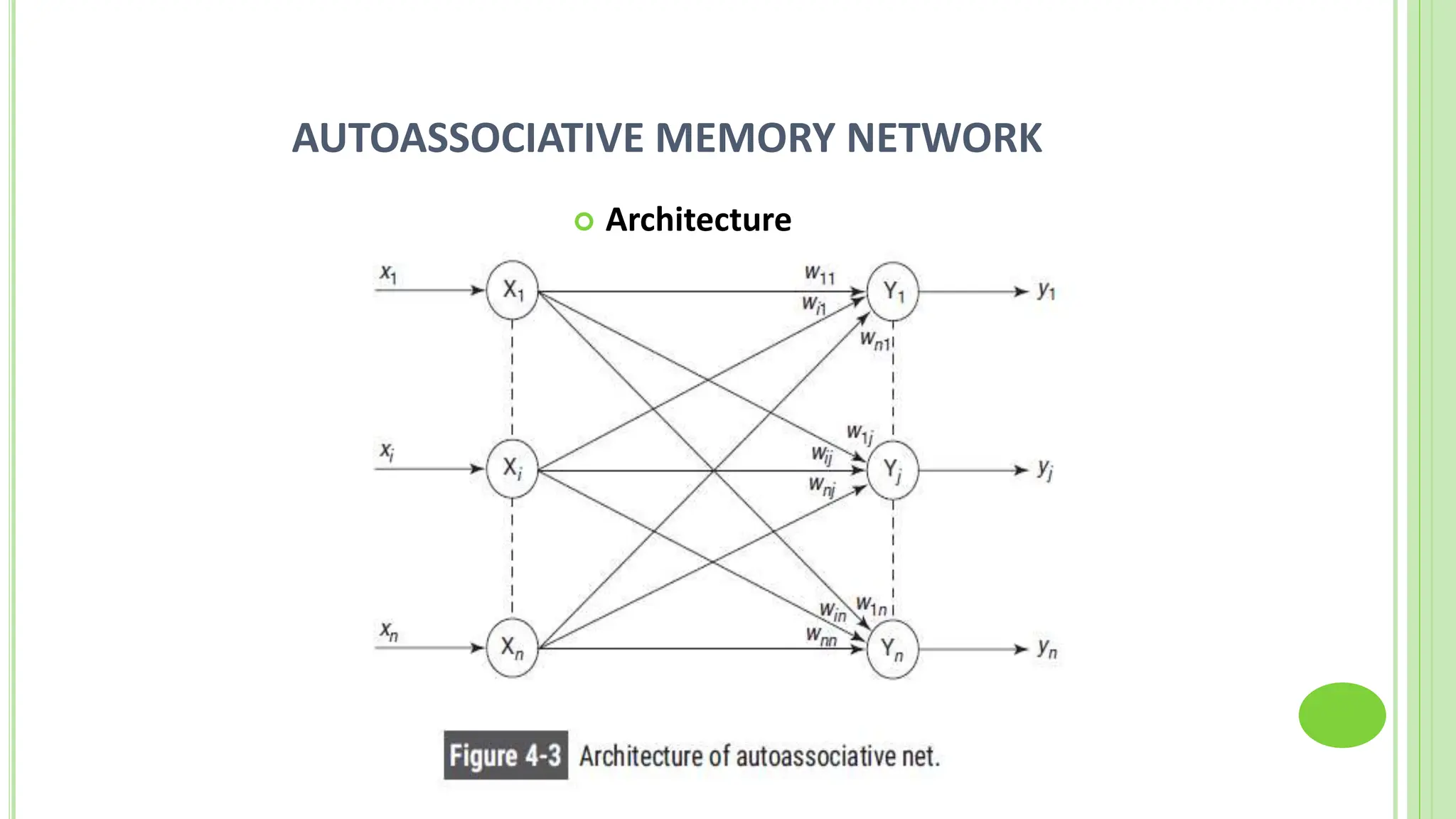
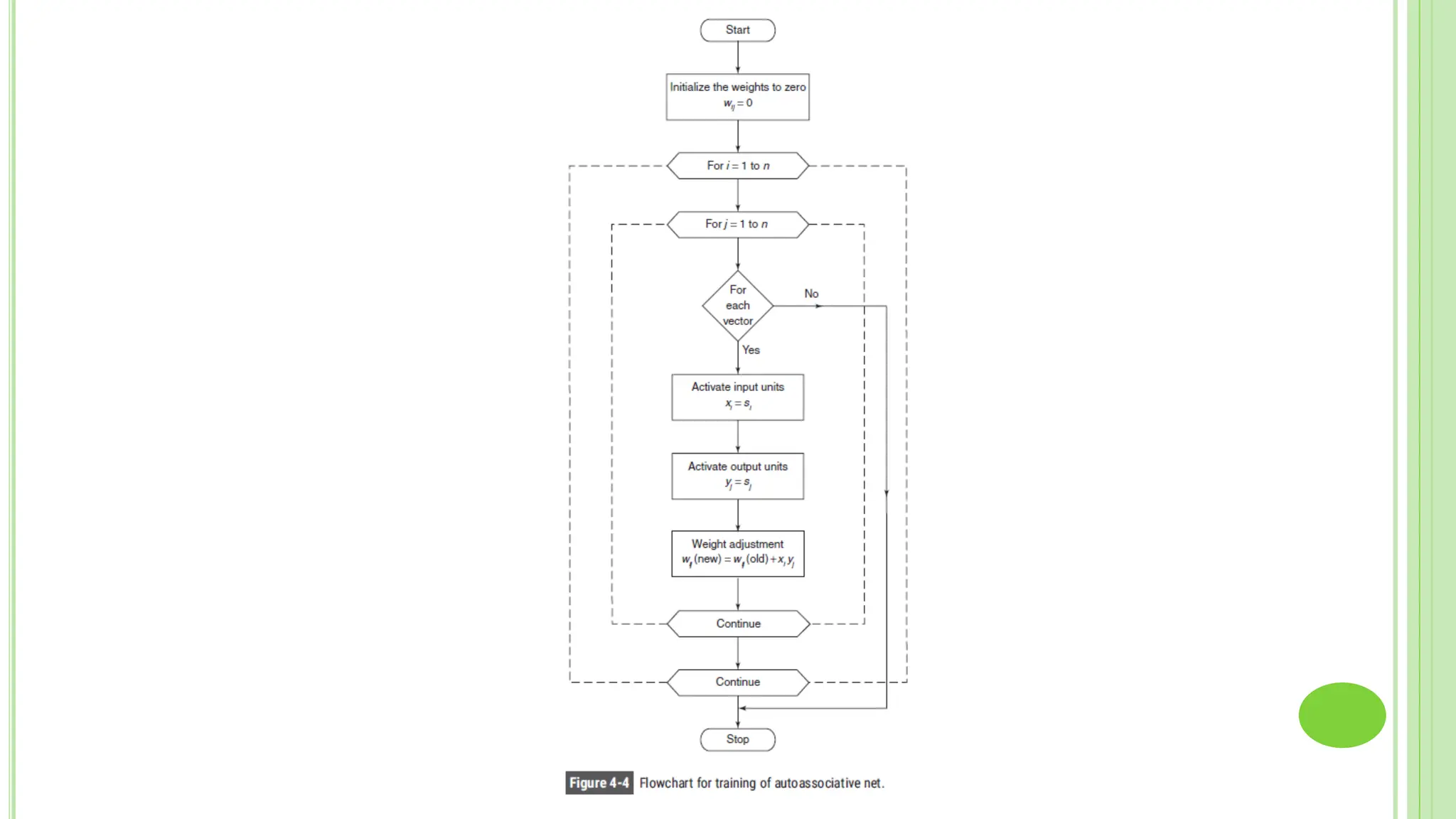
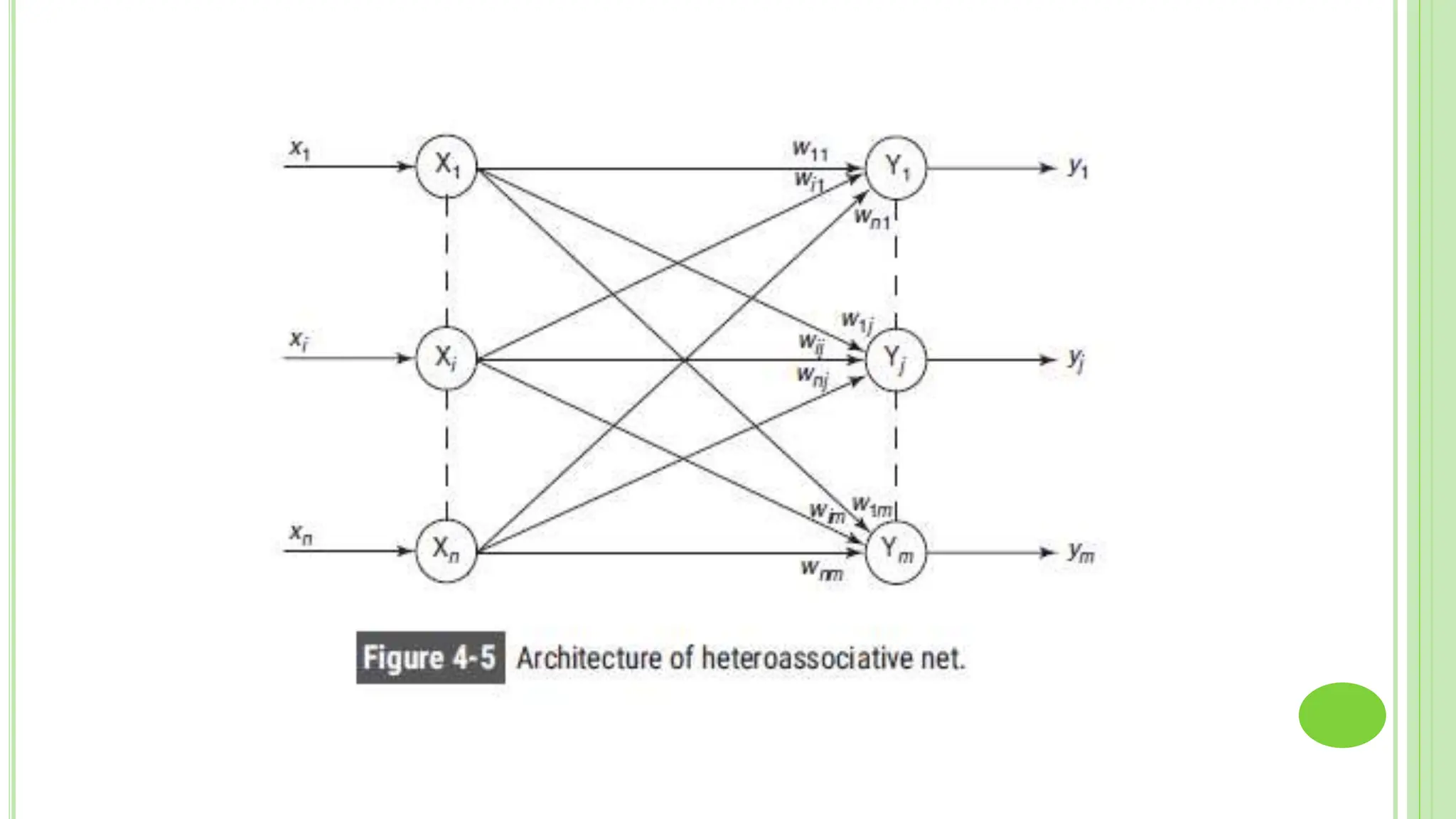
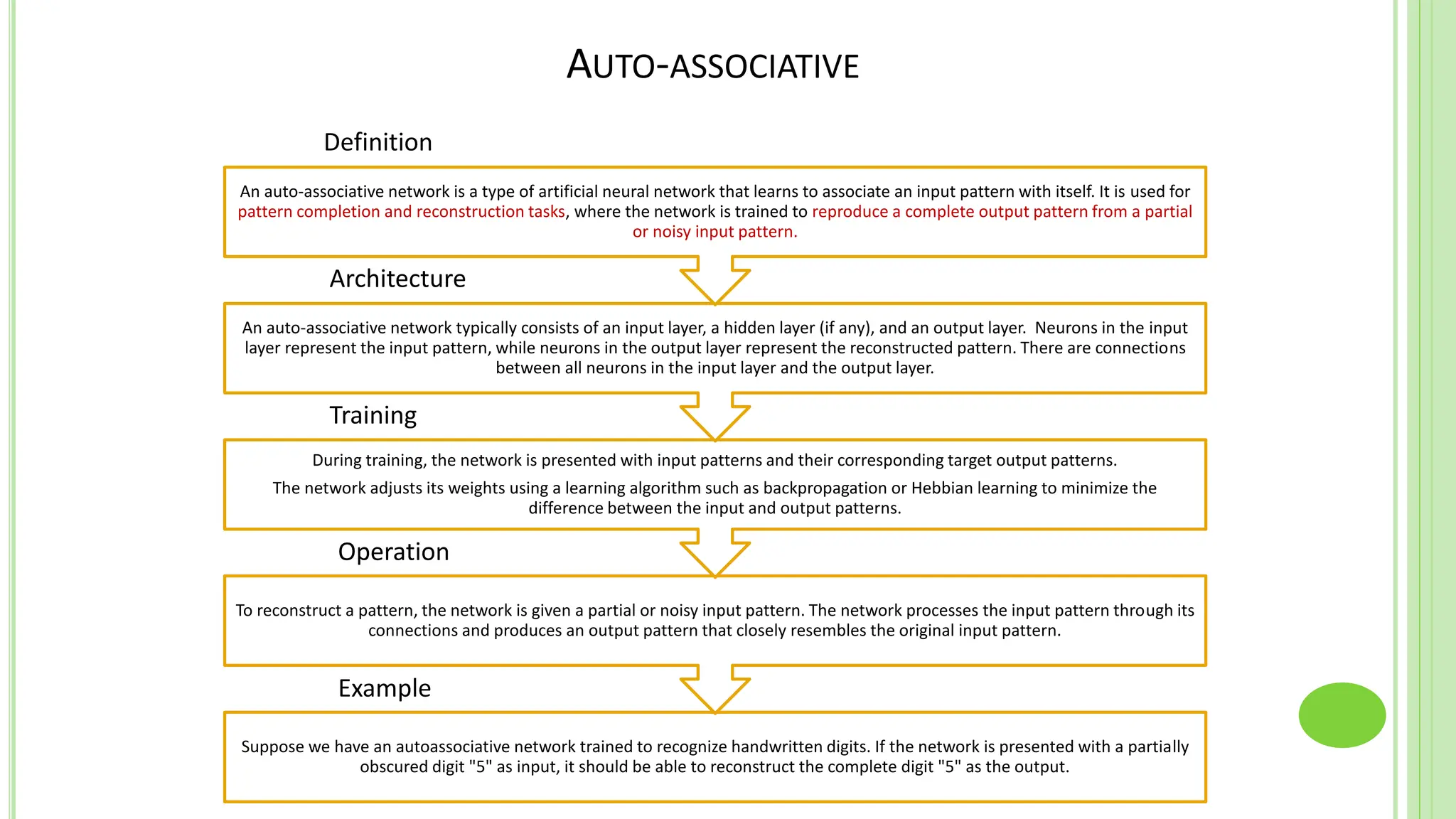
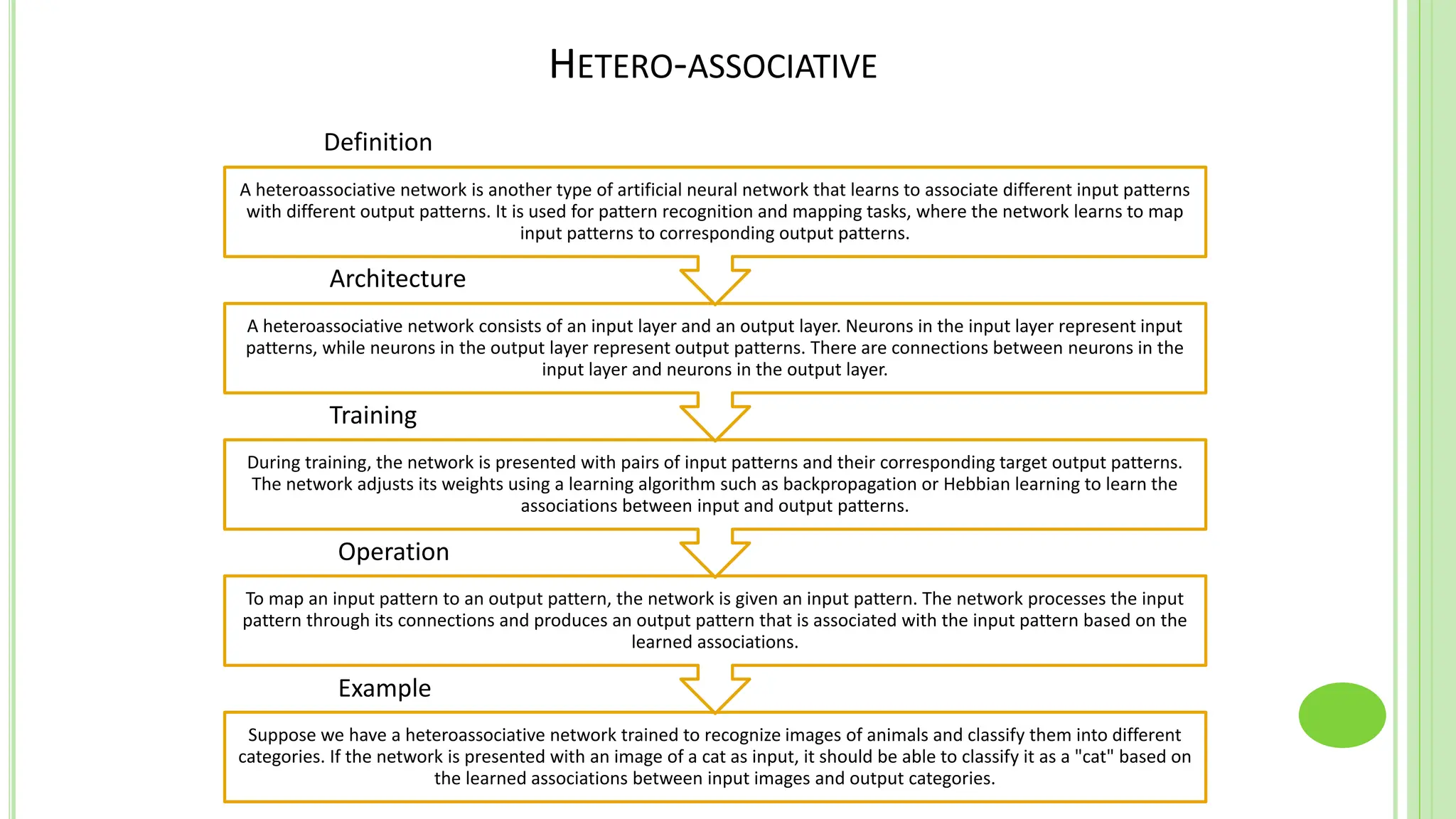
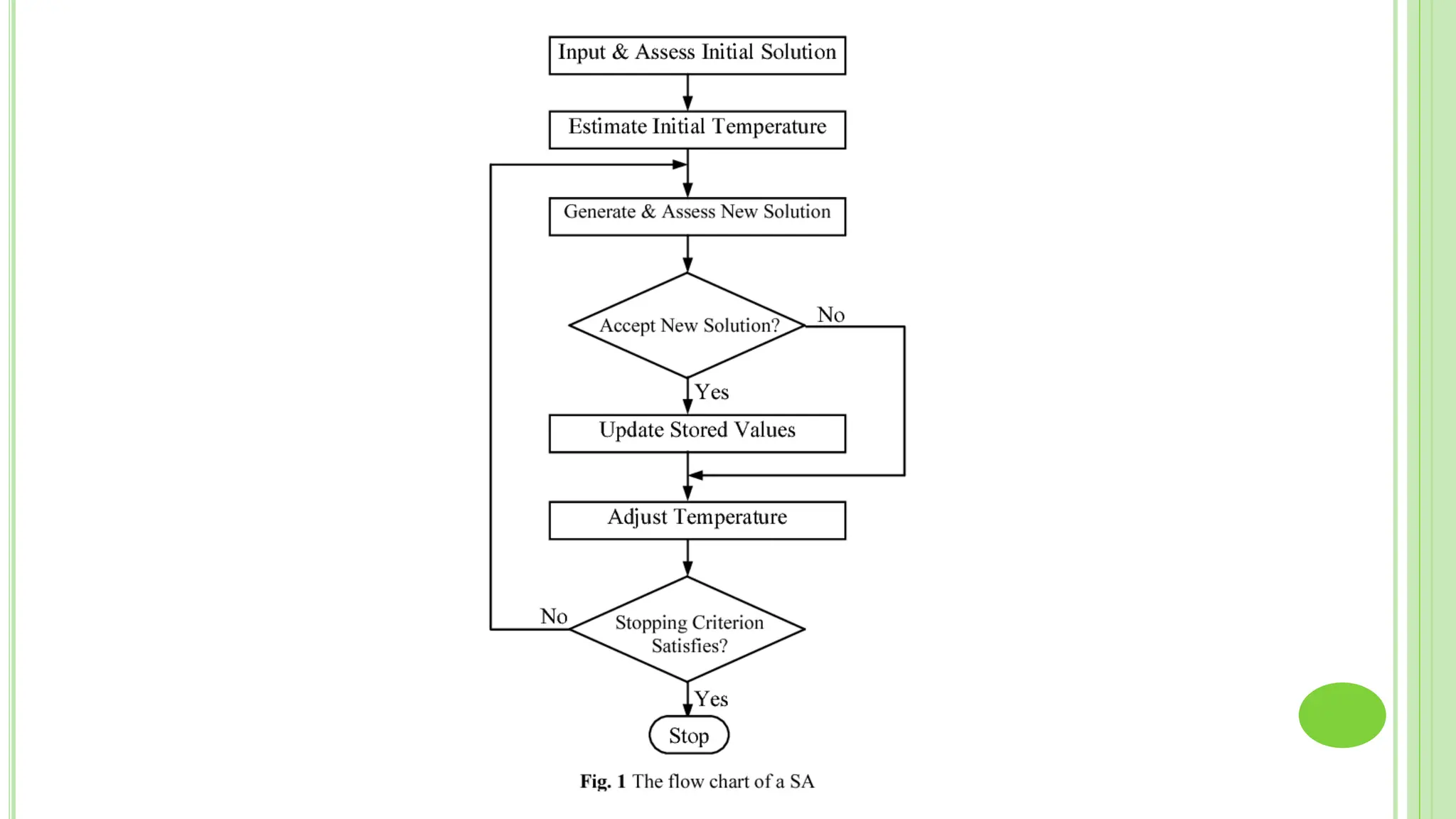
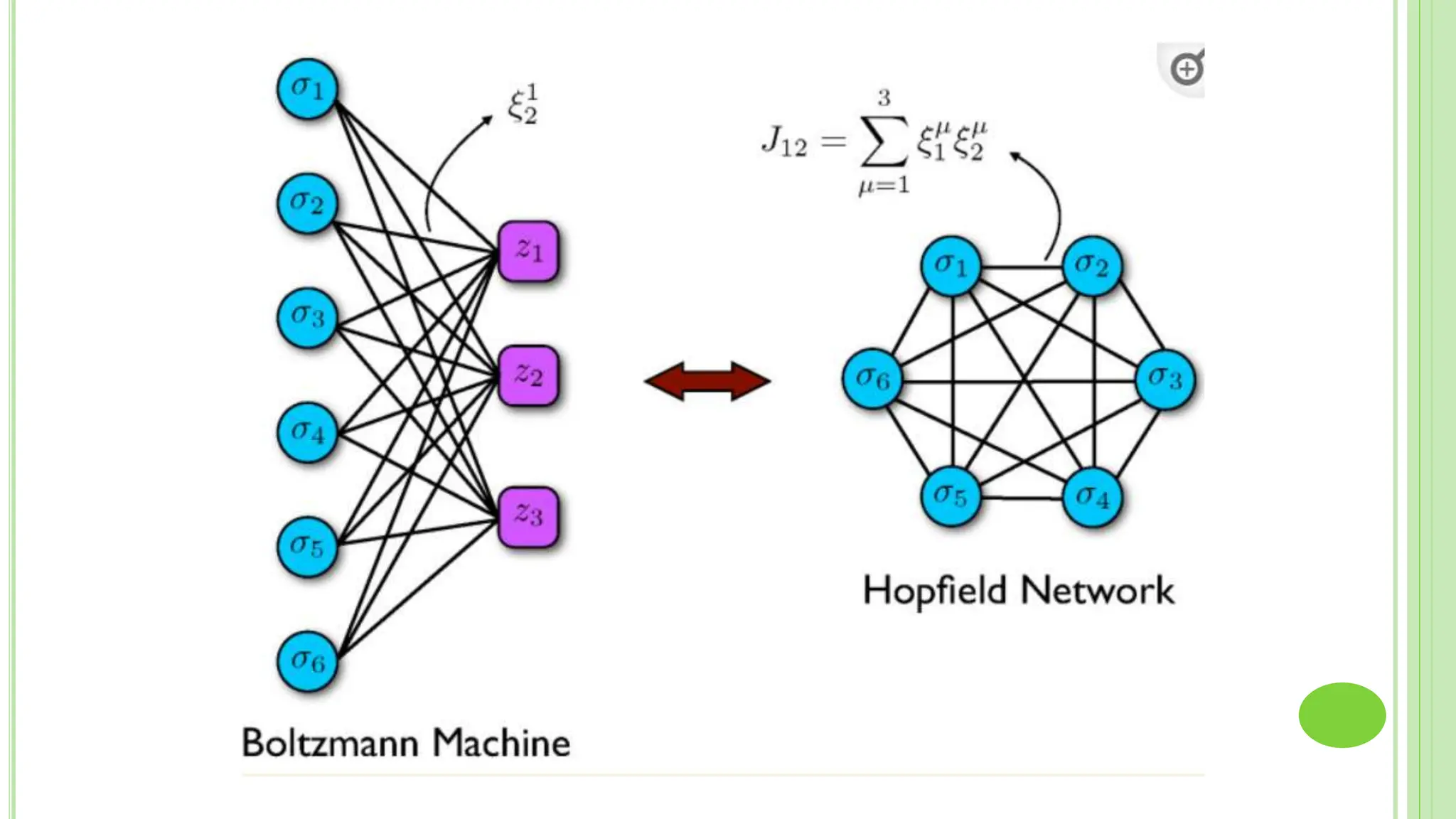
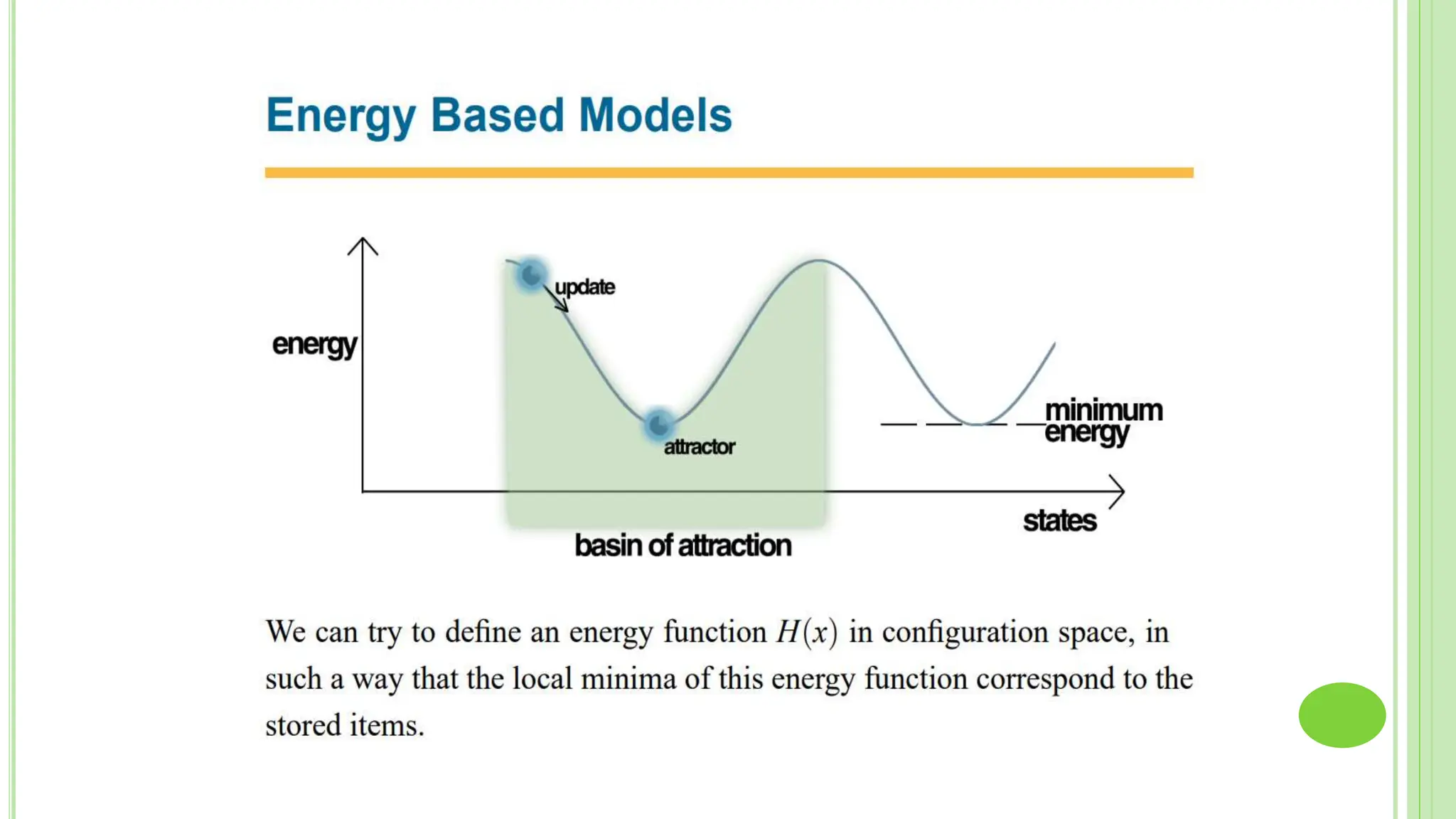
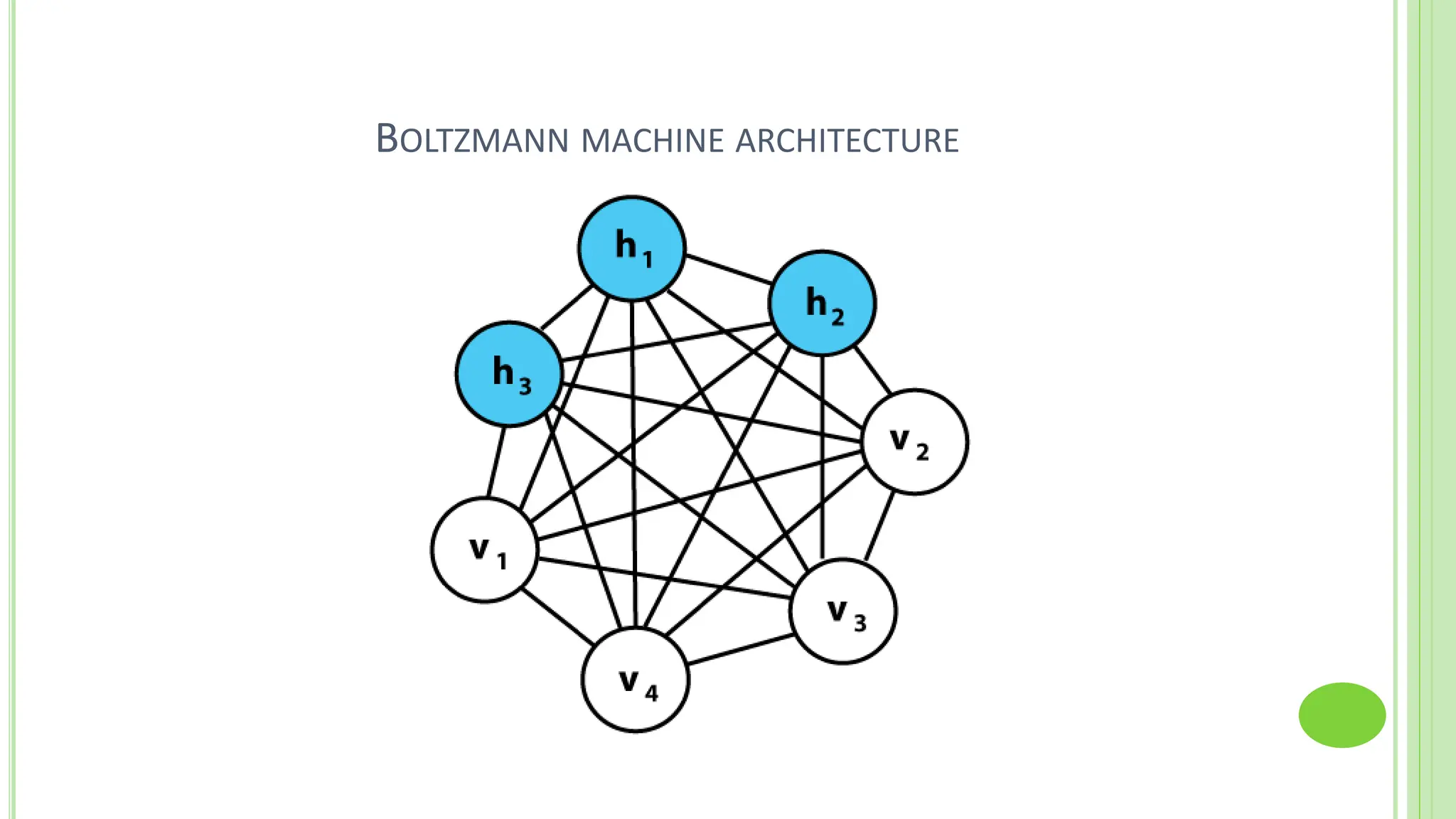
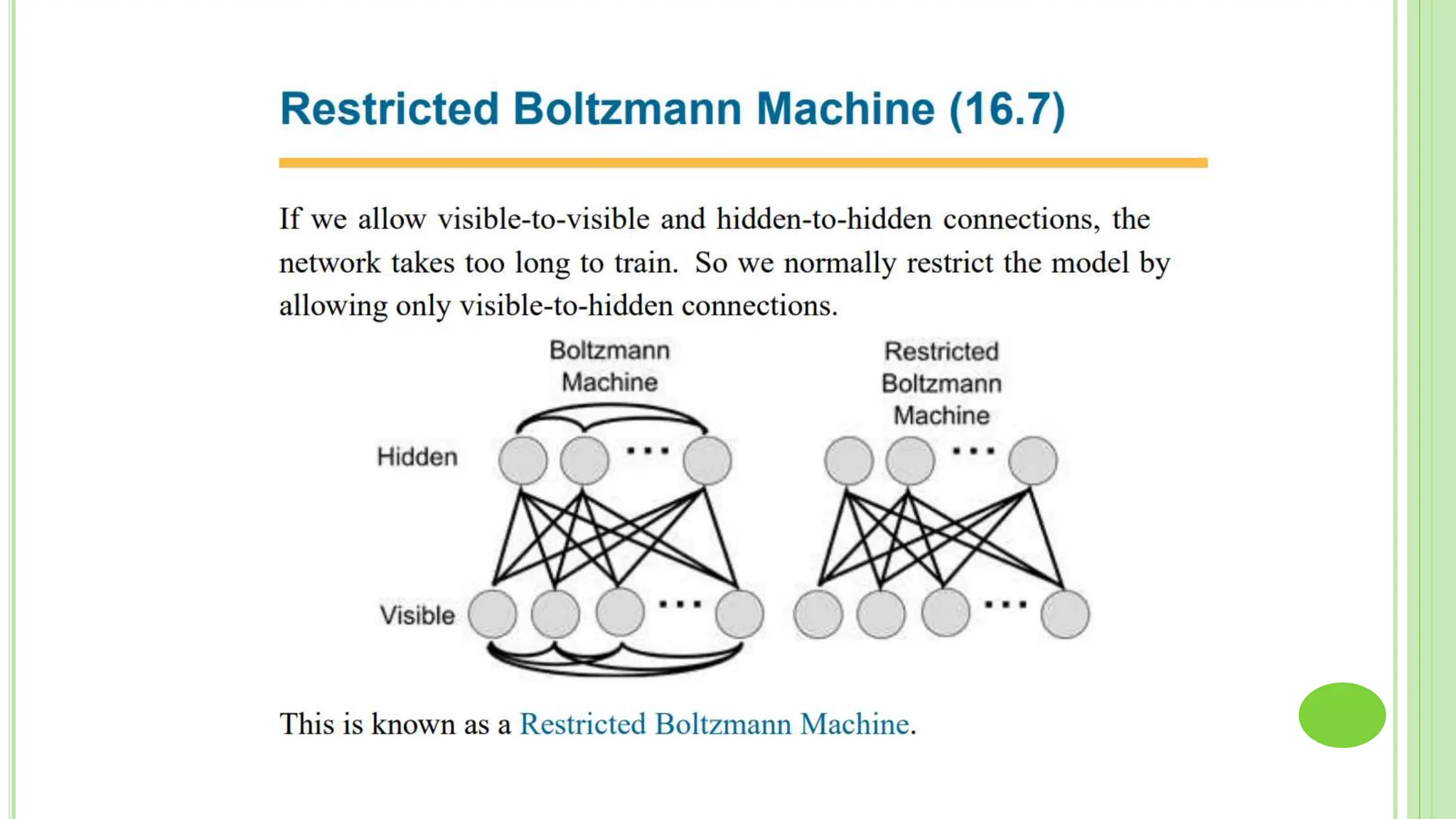
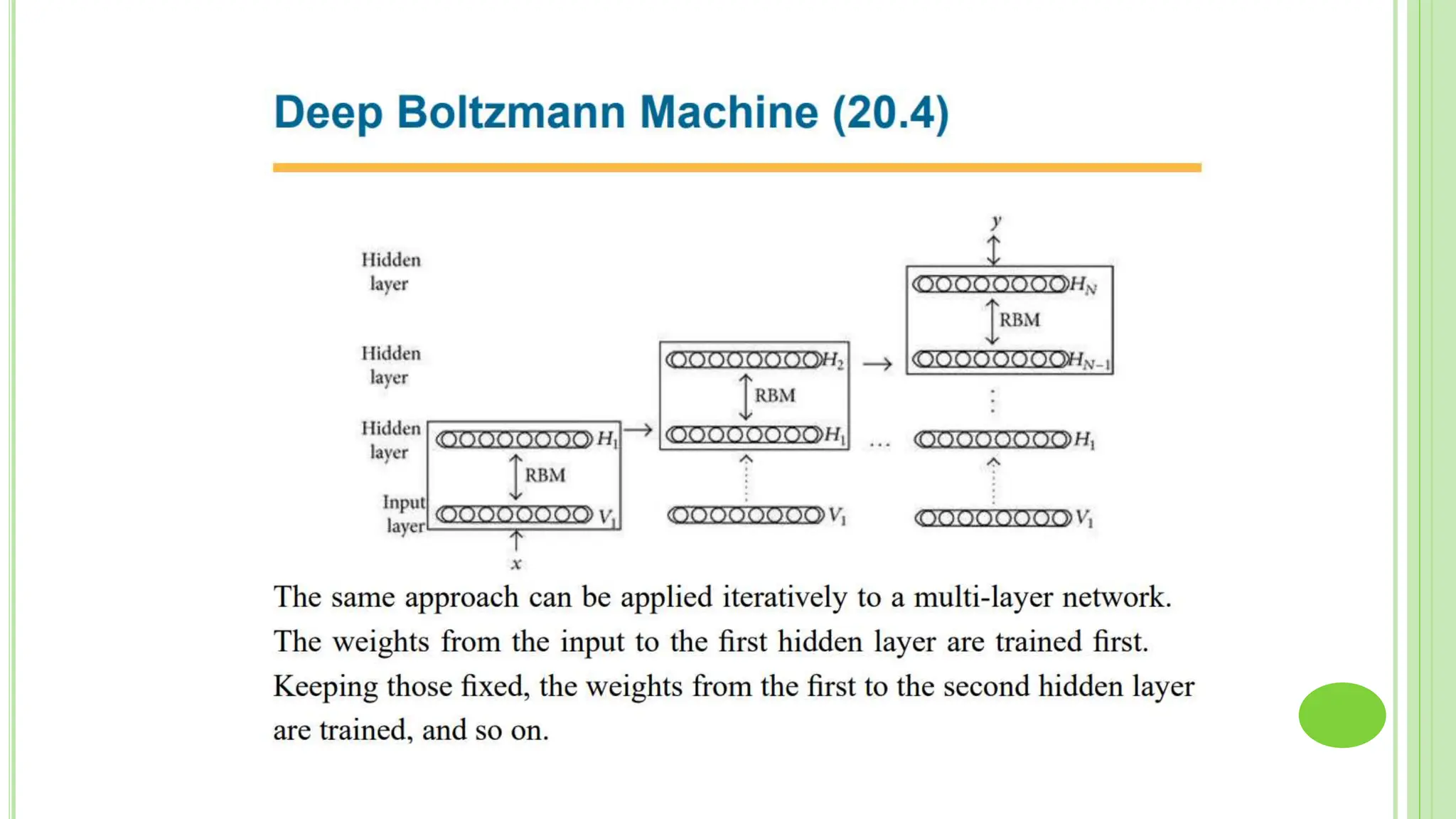
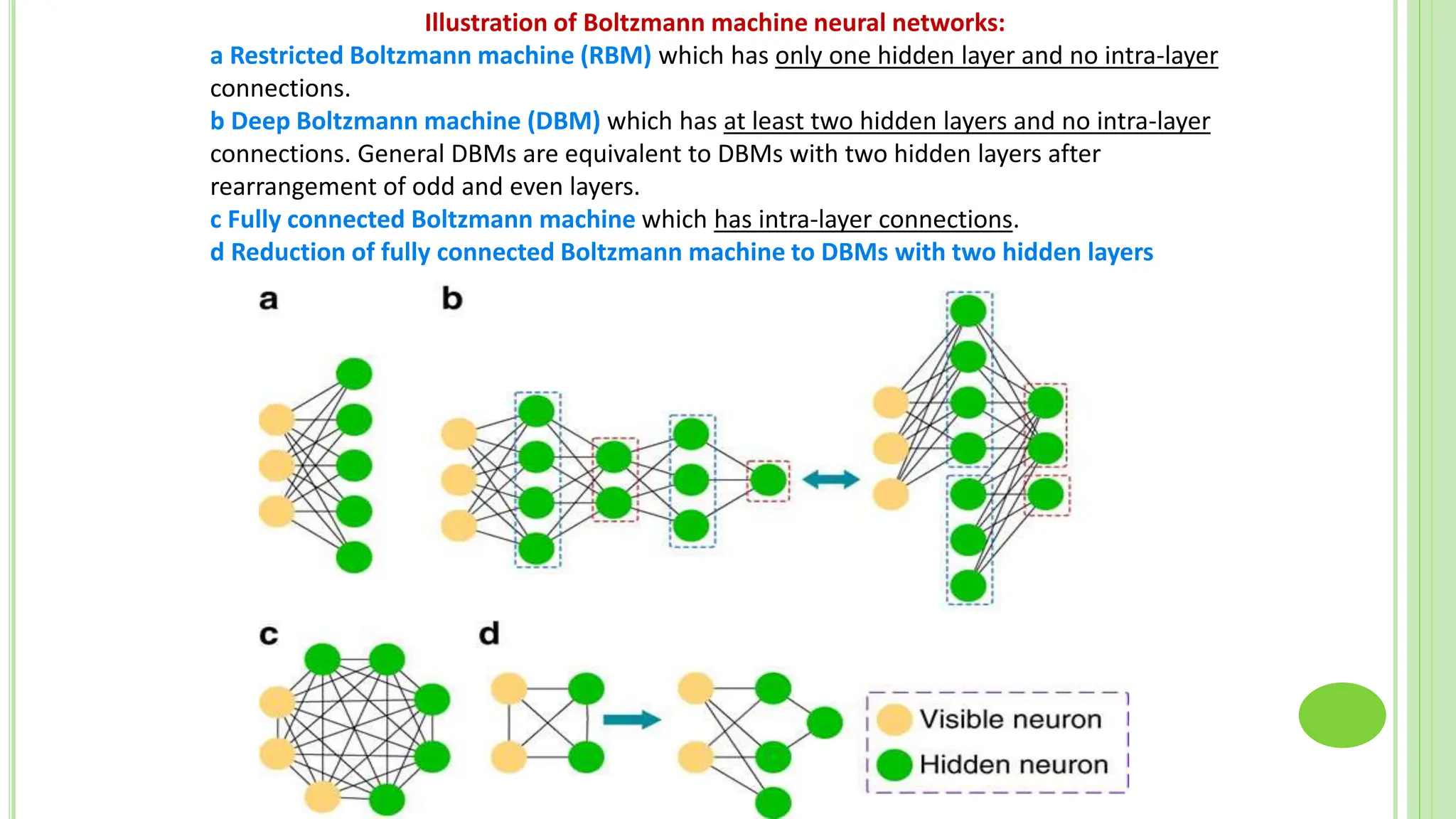
The document discusses associative learning and its applications in artificial neural networks, focusing on concepts like Hopfield networks, Boltzmann machines, and their training algorithms. It outlines key course objectives, outcomes, and features of different types of associative memories, including auto-associative and hetero-associative networks, while emphasizing their noise-resistance and pattern recognition capabilities. Additionally, the text elaborates on optimization techniques such as simulated annealing and the role of temperature in Boltzmann machines.

1. UNIT 3 ASSOCIATIVE LEARNING
Dr Mrs Minakshi Pradeep Atre, Head, Dept of AI & DS

2. CONTENTS
 Introduction
 Associative Learning
 Hopfield network
 Error Performance in Hopfield networks
 Simulated annealing
 Boltzmann machine and Boltzmann learning
 State transition diagram and false minima problem, 3stochastic update,
simulated annealing
 Basic functional units of ANN for pattern recognition tasks:
 Pattern association,
 pattern classification
 and pattern mapping tasks

3. REFERENCES:
 https://solportal.ibe-unesco.org/articles/learning-and-memory-how-the-
brain-codes-knowledge/

4. COURSE OBJECTIVES
1. To provide students with a basic understanding of the fundamentals and
applications of artificial neural networks
2. To identify the learning algorithms and to know the issues of various feed
forward and feedback neural networks.
3. To Understand the basic concepts of Associative Learning and pattern
classification.
4. To solve real world problems using the concept of Artificial Neural Networks.

5. COURSE OUTCOMES
 CO1: Understand the basic features of neural systems and be able to build
the neural model.
 CO2: Perform the training of neural networks using various learning rules.
 CO3: Grasping the use of Associative learning Neural Network
 CO4: Describe the concept of Competitive Neural Networks
 CO5: Implement the concept of Convolutional Neural Networks and its
models
 CO6: Use a new tool /tools to solve a wide variety of real-world problems

6. INTRODUCTION
 An associative memory network can store a set of patterns as memories.
 When an associative memory is being presented with a key pattern, it
responds by producing one of the stored patterns, which closely resembles
or relates to the key pattern.
 Thus, the recall is through association of the key pattern, with the help of
information memorized.
 These types of memories are also called as content-addressable memories
(CAM) in contrast to that of traditional address-addressable memories in
digital computers where stored pattern (in bytes) is recalled by its address.
 It is also a matrix memory as in RAM/ROM.

7. FEATURES CONTINUED…
 The CAM can also be viewed as associating data to address, i.e., for every
data in the memory there is a corresponding unique address.
 Also, it can be viewed as data correlator.
 Here input data is correlated with that of the stored data in the CAM.
 It should be noted that the stored patterns must be unique, i.e., different
patterns in each location.
 If the same pattern exists in more than one location in the CAM, then, even
though the correlation is correct, the address is noted to be ambiguous.

8. CAM ARCHITECTURE

9. FEATURES
 Associative memory makes a parallel search within a stored
data file.
 The concept behind this search is to output any one or all
stored items which match the given search argument and to
retrieve the stored data either completely or partially.
 Two types of associative memories can be differentiated.
 They are auto-associative memory and hetero-associative
memory.
 Both these nets are single-layer nets in which the weights are
determined in a manner that the net stores a set of pattern
associations.

10. FEATURES
 Each of this association is an input–output vector pair, say, s:t.
 If each of the output vectors is same as the input vectors with which it is
associated, then the net is a said to be auto-associative memory net.
 On the other hand, if the output vectors are different from the input vectors
then the net is said to be hetero-associative memory net.

11. HAMMING DISTANCE

12. FEATURES
 The architecture of an associative net may be either feed-forward or
iterative (recurrent).
 As is already known, in a feed-forward net the information flows from the
input units to the output units;
 on the other hand, in a recurrent neural net, there are connections among
the units to form a closed-loop structure.

13. WHAT’S NEXT?
 the training algorithms used for pattern association and various types of
association nets
 Hebb Rule
 Outer Product Rule

14. TRAINING ALGORITHMS FOR PATTERN ASSOCIATION
 Hebb Rule
 Outer Products Rule
 (Delta Rule – can also be used for weight calculations)

15. Flowchart – Hebb Rule

16. Outer Product Rule –
Outer products rule is an alternative method for finding weights of an
associative net.

18. AUTOASSOCIATIVE MEMORY NETWORK
 Theory
 Architecture
 Flowchart for
 Training algorithm
 Testing algorithm

19. AUTOASSOCIATIVE MEMORY NETWORK
 Theory
 In the case of an auto-associative neural net, the training input and the target output
vectors are the same
 The determination of weights of the association net is called storing of vectors
 This type of memory net needs suppression of the output noise at the memory output
 The vectors that have been stored can be retrieved from distorted (noisy) input if the
input is sufficiently similar to it
 The net’s performance is based on its ability to reproduce a stored pattern from a noisy
input.
 It should be noted, that in the case of auto-associative net, the weights on the diagonal
can be set to zero.
 This can be called as auto associative net with no self-connection
 The main reason behind setting the weights to zero is that it improves the net’s ability
to generalize or increase the biological plausibility of the net.
 This may be more suited for iterative nets and when delta rule is being used

20. AUTOASSOCIATIVE MEMORY NETWORK
 Architecture

21. FLOWCHART FOR TRAINING PROCESS

23. TESTING ALGORITHM
AN AUTO-ASSOCIATIVE MEMORY NEURAL NETWORK CAN BE USED TO DETERMINE WHETHER
THE GIVEN INPUT VECTOR IS A “KNOWN” VECTOR OR AN “UNKNOWN” VECTOR.
THE NET IS SAID TO RECOGNIZE A “KNOWN” VECTOR IF THE NET PRODUCES A PATTERN OF
ACTIVATION ON THE OUTPUT UNITS WHICH IS SAME AS ONE OF THE VECTORS STORED IN IT.

24. HETEROASSOCIATIVE MEMORY NETWORK
 Theory
 Architecture
 Flowchart/ algorithm for
 Training
 Testing

25. THEORY
 In case of a heteroassociative neural net, the training input and the target
output vectors are different
 The weights are determined in a way that the net can store a set of pattern
associations
 The association here is a pair of training input target output vector pairs
(s(p), t(p)), with p =1,…,P.
 Each vector s(p) has n components and each vector t(p) has m components
 The determination of weights is done either by using Hebb rule or delta rule.
 The net finds an appropriate output vector, which corresponds to an input
vector x, that may be either one of the stored patterns or a new pattern

26. ARCHITECTURE
 For a heteroassociative net, the training input and target output vectors are
different
 The input layer consists of n number of input units and the output layer
consists of m number of output units
 There exist weighted interconnections between the input and output layers.
 The input and output layer units are not correlated with each other.

29. BIDIRECTIONAL ASSOCIATIVE MEMORY (BAM)
 BAM was developed by Kosko in the year 1988
 BAM network performs forward and backward associative searches for
stored stimulus responses
 BAM is a recurrent heteroassociative pattern-matching network that
encodes binary or bipolar patterns using Hebbian learning rule.
 It associates patterns, say from set A to patterns from set B and vice versa is
also performed.
 BAM neural nets can respond to input from either layers (input layer and
output layer).
 There exist two types of BAM, called discrete and continuous BAM.

30. MATHEMATICAL DISCUSSION

31. HOPFIELD NETWORKS
 John J. Hopfield developed a model in the year 1982 conforming to the
asynchronous nature of biological neurons.
 The networks proposed by Hopfield are known as Hopfield networks and it is
his work that promoted construction of the first analog VLSI neural chip.
 This network has found many useful applications in associative memory and
various optimization problems.
 In this section, two types of network are discussed: discrete and continuous
Hopfield networks

32. DISCRETE HOPFIELD NETWORK
 The Hopfield network is an auto-associative fully interconnected single-layer
feedback network.
 It is also a symmetrically weighted network.
 When this is operated in discrete line fashion it is called as discrete Hopfield
network and its architecture as a single-layer feedback network can be
called as recurrent.
 The network takes two-valued inputs: binary (0, 1) or bipolar (+1, –1);
 the use of bipolar inputs makes the analysis easier.
 The network has symmetrical weights with no self-connections, i.e.,

34. ASSOCIATIVE NETWORKS
 Definition and Concept:
 Associative learning refers to the process through which an organism or a
machine learns to associate two or more stimuli or events.
 In the context of artificial neural networks (ANNs), associative learning
involves the network learning to associate certain input patterns with
specific output patterns.
 This enables the network to recognize and recall patterns even when
presented with partial or noisy inputs.
 Example- a person with specific features or typical attire (wearing typical
shirt many times a week)

35. ASSOCIATIVE LEARNING IN PATTERN RECOGNITION TASKS
 Associative learning allows ANNs to learn complex relationships between
input and output patterns
 It enables tasks such as pattern association, where the network is trained to
produce a specific output pattern in response to a given input pattern
 Additionally, associative learning facilitates pattern completion, where the
network can reconstruct missing or noisy parts of an input pattern to
produce a complete output pattern.

36. ASSOCIATIVE LEARNING APPLICATIONS
 Memory retrieval systems
 Auto-associative and hetero-associative memory models
 Content-addressable memory systems
 Pattern recognition and classification tasks
 Neural network-based recommender systems
How are they
different?

37. IMPORTANT POINTS
 Associative networks are noise- resistant
 Noise-resistant – means- it will retrieve the data despite the partial
information is presented as the input
 For example – when you see your friend from a larger distance, you are not
able to see his face clearly but you recognise him by his features/ attire/
posture/ style
 Simultaneously they are highly interactive which may produce errors
 For example – When a person sitting in the bank meets you in the market,
you can’t locate him many a times because there might have been an error
to map his surroundings

38. AUTO-ASSOCIATIVE
Suppose we have an autoassociative network trained to recognize handwritten digits. If the network is presented with a partially
obscured digit "5" as input, it should be able to reconstruct the complete digit "5" as the output.
To reconstruct a pattern, the network is given a partial or noisy input pattern. The network processes the input pattern through its
connections and produces an output pattern that closely resembles the original input pattern.
During training, the network is presented with input patterns and their corresponding target output patterns.
The network adjusts its weights using a learning algorithm such as backpropagation or Hebbian learning to minimize the
difference between the input and output patterns.
An auto-associative network typically consists of an input layer, a hidden layer (if any), and an output layer. Neurons in the input
layer represent the input pattern, while neurons in the output layer represent the reconstructed pattern. There are connections
between all neurons in the input layer and the output layer.
An auto-associative network is a type of artificial neural network that learns to associate an input pattern with itself. It is used for
pattern completion and reconstruction tasks, where the network is trained to reproduce a complete output pattern from a partial
or noisy input pattern.
Training
Definition
Architecture
Operation
Example

39. HETERO-ASSOCIATIVE
Suppose we have a heteroassociative network trained to recognize images of animals and classify them into different
categories. If the network is presented with an image of a cat as input, it should be able to classify it as a "cat" based on
the learned associations between input images and output categories.
To map an input pattern to an output pattern, the network is given an input pattern. The network processes the input
pattern through its connections and produces an output pattern that is associated with the input pattern based on the
learned associations.
During training, the network is presented with pairs of input patterns and their corresponding target output patterns.
The network adjusts its weights using a learning algorithm such as backpropagation or Hebbian learning to learn the
associations between input and output patterns.
A heteroassociative network consists of an input layer and an output layer. Neurons in the input layer represent input
patterns, while neurons in the output layer represent output patterns. There are connections between neurons in the
input layer and neurons in the output layer.
A heteroassociative network is another type of artificial neural network that learns to associate different input patterns
with different output patterns. It is used for pattern recognition and mapping tasks, where the network learns to map
input patterns to corresponding output patterns.
Training
Definition
Architecture
Operation
Example

40. HOPFIELD NETWORKS
 Hopfield networks are a type of recurrent artificial neural network
introduced by John Hopfield in 1982
 They are characterized by their ability to store and retrieve patterns through
recurrent connections between neurons
 Hopfield networks are often used for associative memory tasks and
optimization problems
 Architecture:
 A Hopfield network consists of a set of interconnected neurons, where each
neuron is connected to every other neuron in the network
 The connections between neurons are symmetric and have fixed weights
 The network operates in a recurrent manner, where the state of each
neuron is updated iteratively based on the states of its neighboring neurons

41. ERROR PERFORMANCE IN HOPFIELD NETWORKS
 The error performance of a Hopfield network refers to its ability to
accurately store and recall patterns in the presence of noise or corruption in
the input data.
 Errors in Hopfield networks can arise due to various factors,
 including –
 network size,
 pattern complexity,
 and the presence of spurious attractors

42. FACTORS AFFECTING ERROR PERFORMANCE
 Network architecture and connectivity
 Pattern representation and encoding
 Learning and update rules
 Noise levels in the input data

43. IMPROVEMENT TECHNIQUES:
 Techniques to improve error performance in Hopfield networks include:
 Increasing network size and connectivity
 Using advanced learning algorithms and update rules
 Employing noise reduction and error correction mechanisms
 Preprocessing input data to enhance pattern separation and discrimination

44. SIMULATED ANNEALING
 Introduction
 Simulated annealing is a probabilistic optimization technique
inspired by the process of annealing in metallurgy
 It is used to find near-optimal solutions to optimization
problems by simulating the physical process of annealing,
where a material is gradually cooled to reach a low-energy
state
 In simulated annealing, a system starts at an initial state, and
at each iteration, it randomly explores neighboring states and
accepts or rejects them based on a probability distribution
 The acceptance probability decreases over time, allowing the
system to escape local optima and explore the solution space
more effectively.

45. ROLE OF SIMULATED ANNEALING IN OPTIMIZATION PROBLEMS
 Simulated annealing is particularly useful in optimization problems where
the objective function is non-linear, discontinuous, or noisy.
 Its main role is to efficiently search the solution space to find a near-optimal
solution, even in the presence of local optima or plateaus.
Simulated annealing is effective because it allows the system to:
 Explore a wide range of solutions by accepting worse solutions with a certain
probability, thereby preventing the algorithm from getting stuck in local
optima.
 Gradually decrease the acceptance probability over time, ensuring
convergence towards a global optimum while allowing for exploration of the
solution space.
Optimization is the best
possible solution

46. Why Simulated Annealing in
Optimization Problems –
its ability to effectively optimize
non-linear and discontinuous
objective functions

47. HOW TO IMPLEMENT SIMULATED ANNEALING
 Defining an objective function to be minimized, such as the error between
the network's predictions and the actual targets
 Initializing the network's parameters (e.g., weights and biases) randomly or
using a predefined strategy
 Iteratively updating the network's parameters by exploring neighboring
parameter configurations and accepting or rejecting them based on the
acceptance probability
 Gradually decreasing the acceptance probability over time to allow the
network to converge towards a configuration that minimizes the objective
function.

49. BRIDGING THE GAP BETWEEN HOPFIELD & BOLTZMANN

50. THE HOPFIELD MODEL AND THE BOLTZMANN MACHINE ARE
AMONG THE MOST POPULAR EXAMPLES OF NEURAL
NETWORKS.
THE LATTER, WIDELY USED FOR CLASSIFICATION AND FEATURE
DETECTION, IS ABLE TO EFFICIENTLY LEARN A GENERATIVE
MODEL FROM OBSERVED DATA AND CONSTITUTES THE
BENCHMARK FOR STATISTICAL LEARNING
Reference –
Boltzmann Machines as Generalized Hopfield
Networks: A Review of Recent Results and
Outlooks
Chiara Marullo† and Elena Agliari*†

52. https://www.cse.unsw.edu.au/~cs9444/17s2/lect/1page/11_Boltzmann.pdf

66. IN THE CONTEXT OF NEURAL NETWORKS, SUCH AS
BOLTZMANN MACHINES, THE TERM "TEMPERATURE" IS NOT
RELATED TO THE PHYSICAL TEMPERATURE OF NEURONS OR
THE NETWORK ITSELF.
INSTEAD, IT IS A CONCEPT BORROWED FROM STATISTICAL
PHYSICS AND USED AS A PARAMETER IN THE LEARNING
ALGORITHMS TO CONTROL THE STOCHASTIC BEHAVIOR OF
THE NETWORK.

67. HERE'S HOW TEMPERATURE COMES INTO THE PICTURE IN NEURAL
NETWORKS:
 Boltzmann Machines:
 In Boltzmann Machines, the concept of temperature is derived
from the Boltzmann distribution in statistical physics. The
temperature parameter affects the probability of state
transitions during the stochastic update process.
 A higher temperature corresponds to a higher probability of
accepting state transitions, leading to more exploration of the
state space. Conversely, a lower temperature corresponds to a
lower probability of accepting state transitions, promoting
exploitation of promising regions in the state space.
 The temperature parameter is used in the Gibbs sampling or
Metropolis-Hastings algorithm, which are stochastic update
rules employed in Boltzmann Machines.

70. BOLTZMANN MACHINE
HTTPS://WWW.ENGATI.COM/GLOSSARY/BOLTZMANN-MACHINE

71. BOLTZMANN MACHINE AND BOLTZMANN LEARNING
 A Boltzmann Machine is a type of recurrent neural network that uses
stochastic learning algorithms to find optimal network states and model
complex data distributions
 Boltzmann machine is developed by Geoffrey Hinton and Terry Sejnowski in
1985 and is named after Ludwig Boltzmann, an Austrian physicist – who
came up with the Boltzmann distribution
 A Boltzmann machine is an unsupervised deep learning model in which
every node is connected to every other node
 The nodes make binary decisions with some level of bias
 These machines being not deterministic deep learning models, they are
called as stochastic or generative deep learning models

72. The Boltzmann distribution is a probability distribution
that gives the probability of a system being in a certain
state as a function of that state's energy and the
temperature of the system.
It was formulated by Ludwig Boltzmann in 1868 and is
also known as the Gibbs distribution.

73. AIM OF THE BOLTZMANN MACHINE
 The main aim of a Boltzmann machine is to optimize the solution of a
problem
 To do this, it optimizes the weights and quantities related to the specific
problem that is assigned to it
 This technique is employed when the main aim is to create mapping and to
learn from the attributes and target variables in the data
 If you seek to identify an underlying structure or the pattern within the
data, unsupervised learning methods for this model are regarded to be more
useful
 Some of the most widely used unsupervised learning methods are
clustering, dimensionality reduction, anomaly detection and creating
generative models

74. PURPOSE
 All of these techniques have a different objective of detecting patterns like
identifying latent grouping, finding irregularities in the data, or even
generating new samples from the data that is available
 You can even stack these networks in layers to build deep neural
networks that capture highly complicated statistics
 Restricted Boltzmann machines are widely used in the domain of imaging
and image processing as well because they have the ability to model
continuous data that are common to natural images
 They are even used to solve complicated quantum mechanical many-particle
problems or classical statistical physics problems like the Ising and Potts
classes of models

76. BOLTZMANN MACHINE AND BOLTZMANN LEARNING
 It is similar to error-correction learning and is used during supervised
training.
 These machines can be trained to produce any desired output from a given
input, through a blend of supervised and unsupervised learning methods,
making it a versatile and powerful tool in the realm of artificial
intelligence and machine learning
 In this algorithm, the state of each individual neuron, in addition to the
system output, are taken into account.
 Restricted Boltzmann machine (RBM) is an undirected graphical model that
falls under deep learning algorithms.
 It plays an important role in dimensionality reduction, classification and regression
 RBM is the basic block of Deep-Belief Networks
 It is a shallow, two-layer neural networks.

77. ARCHITECTURE OF BOLTZMANN MACHINES
 A Boltzmann machine has two kinds of nodes
 Visible nodes:
These are nodes that can be measured and are measured
 Hidden nodes:
These are nodes that cannot be measured or are not measured
 Boltzmann machine can be called a stochastic Hopfield network which has
hidden units
 It has a network of units with an ‘energy’ defined for the overall network
 Boltzmann machines seek to reach thermal equilibrium.
 It essentially looks to optimize global distribution of energy
 But the temperature and energy of the system are relative to laws of
thermodynamics and are not literal

78.  Boltzmann machines are non-deterministic (stochastic) generative Deep
Learning models that only have two kinds of nodes - hidden and visible
nodes
 They don’t have any output nodes, and that’s what gives them the non-
deterministic feature
 They learn patterns without the typical 1 or 0 type output through which
patterns are learned and optimized using Stochastic Gradient Descent

79. BOLTZMANN MACHINE ARCHITECTURE

80.  A major difference is that unlike other traditional networks which don’t have
any connections between the input nodes, Boltzmann Machines have
connections among the input nodes
 Every node is connected to all other nodes irrespective of whether they are
input or hidden nodes
 This enables them to share information among themselves and self-generate
subsequent data.
 We would only measure what’s on the visible nodes and not what’s on the
hidden nodes.
 After the input is provided, the Boltzmann machines are able to capture all
the parameters, patterns and correlations among the data.
 It is because of this that they are known as deep generative models and they
fall into the class of Unsupervised Deep Learning

81. BOLTZMANN LEARNING
 A Boltzmann machine is made up of a learning algorithm that enables it to
discover interesting features in datasets composed of binary vectors
 The learning algorithm tends to be slow in networks that have many layers
of feature detectors but it is possible to make it faster by implementing a
learning layer of feature detectors
 They use stochastic binary units to reach probability distribution equilibrium
(to minimize energy)
 It is possible to get multiple Boltzmann machines to collaborate together to
form far more sophisticated systems like deep belief networks

82. HOW DOES A BOLTZMANN MACHINE WORK?
 Boltzmann Machines use a combination of visible and hidden nodes to learn
patterns and represent complex data distributions.
 The learning process involves updating the weights connecting the nodes
based on the energy function, which is derived from Boltzmann’s probability
distribution.
 The network eventually reaches an equilibrium state, where the weight
adjustments become minimal, signifying convergence to an optimal solution.

83. WHAT ARE THE TYPES OF BOLTZMANN MACHINES?
 There are two main types of Boltzmann Machines: Restricted Boltzmann
Machines (RBMs) and Deep Boltzmann Machines (DBMs)
 RBMs have a simpler structure, with only one layer of visible nodes and one
layer of hidden nodes
 DBMs, on the other hand, have multiple layers of hidden nodes, allowing
them to represent more complex data patterns and perform deep learning
tasks

84. TYPES OF BOLTZMANN MACHINES
 1. Restricted Boltzmann Machines (RBMs)
 2. Deep Belief Networks (DBNs)
 3. Deep Boltzmann Machines (DBMs)

85. 1. RESTRICTED BOLTZMANN MACHINES (RBMS)
 While in a full Boltzmann machine all the nodes are connected to each other
and the connections grow exponentially, an RBM has certain restrictions
with respect to node connections.
 In a Restricted Boltzmann Machine, hidden nodes cannot be connected to
each other while visible nodes are connected to each other.

89. 2. DEEP BELIEF NETWORKS (DBNS)
 In a Deep Belief Network, multiple Restricted Boltzmann Machines are
stacked, such that the outputs of the first RBM are the inputs of the
subsequent RBM
 The connections within individual layers are undirected, while the
connections between layers are directed
 However, there is an exception here. The connection between the top two
layers is undirected.
 A deep belief network can either be trained using a Greedy Layer-wise
Training Algorithm or a Wake-Sleep Algorithm.

90. 3. DEEP BOLTZMANN MACHINES (DBMS)
 Deep Boltzmann Machines are very similar to Deep Belief Networks.
 The difference between these two types of Boltzmann machines is that
while connections between layers in DBNs are directed, in DBMs, the
connections within layers, as well as the connections between the layers,
are all undirected.

92. HOW DO BOLTZMANN MACHINES DIFFER FROM TRADITIONAL NEURAL
NETWORKS?
 Boltzmann Machines differ from traditional neural networks in their learning
algorithm, structure, and equilibrium state.
 While traditional neural networks use deterministic learning algorithms like
backpropagation, Boltzmann Machines use stochastic learning based on
statistical mechanics.
 Additionally, Boltzmann Machines are recurrent networks, which means
they include cycles in their connections, unlike the feed-forward structure of
most traditional networks.
 Also, their goal is to reach an equilibrium state where the network converges
to an optimal solution.

94. WHAT ARE THE APPLICATIONS OF BOLTZMANN MACHINES?
 Boltzmann Machines have been applied in various fields, including artificial
intelligence, computer vision, natural language processing, and pattern
recognition.
 Some specific applications include image and speech recognition,
dimensionality reduction, feature extraction, and collaborative filtering for
recommendation systems.

95.  As a result, this technology finds usage in a wide range of applications that
require knowledge discovery, pattern recognition, and optimization,
impacting fields such as artificial intelligence, machine learning, and deep
learning.
 Its significance lies in the innovative approach it brings to improve
computation, provide better learning algorithms, and consequently
revolutionize the way machines interact with and make sense of complex
data sets.

96. FEATURES
 The Boltzmann Machine is a type of stochastic artificial neural network that
serves as an essential tool for identifying optimal solutions in large and
complex search spaces.
 One of the primary uses for these machines is resolving issues concerning
optimization, machine learning, and pattern recognition.
https://www.devx.com/terms/boltzmann-machine/

97. WHAT’S DIFFERENT IN BOLTZMANN?
However, instead of a direct difference between
the result value and the desired value, we take the
difference between the probability distributions
of the system.
Unlike feedforward neural networks, the
connections between the nodes of the hidden
layer and the visible layer's nodes in the restricted
Boltzmann machines can be bi-directionally
connected.

98. SUMMARY OF TYPES OF BOLTZMANN MACHINE

99. RESTRICTED BOLTZMANN – ALL NODES ARE CONNECTED TO EACH OTHER –
NO OUTPUT NODE CONCEPT

100. DEEP BELIEF NETWORKS (DBNS)- MULTIPLE RESTRICTED
BOLTZMANN MACHINES ARE STACKED, SUCH THAT THE
OUTPUTS OF THE FIRST RBM ARE THE INPUTS OF THE
SUBSEQUENT RBM

101. DEEP BELIEF NETWORKS (DBNS)- RBMS STACKED TOGETHER – AND
DIRECTED

102. DEEP BOLTZMANN MACHINES -CONNECTIONS BETWEEN
LAYERS IN DBNS ARE DIRECTED, IN DBMS, THE
CONNECTIONS WITHIN LAYERS, AS WELL AS THE
CONNECTIONS BETWEEN THE LAYERS, ARE ALL UNDIRECTED.

103. STATE TRANSITION DIAGRAM
 Boltzmann Machines can be represented by state transition diagrams
 Each node in the diagram represents a neuron, and the directed edges
represent the connections between neurons with associated weights
 In Boltzmann Machines, neurons update their states asynchronously or in
parallel based on the states of neighboring neurons and the weights
connecting them.
 This updating process continues iteratively until the system reaches an
equilibrium state or a certain convergence criteria is met
 The state transition diagram helps visualize how the states of neurons
change over time and how information flows through the network during
the learning process

104. Illustration of Boltzmann machine neural networks:
a Restricted Boltzmann machine (RBM) which has only one hidden layer and no intra-layer
connections.
b Deep Boltzmann machine (DBM) which has at least two hidden layers and no intra-layer
connections. General DBMs are equivalent to DBMs with two hidden layers after
rearrangement of odd and even layers.
c Fully connected Boltzmann machine which has intra-layer connections.
d Reduction of fully connected Boltzmann machine to DBMs with two hidden layers

106. FALSE MINIMA PROBLEM
 Boltzmann Machines, like many other neural networks, are prone to getting
trapped in local minima during the learning process.
 The false minima problem refers to situations where the learning algorithm
converges to suboptimal solutions that are not the global minima of the
energy landscape.
 This problem arises due to the non-convex and high-dimensional nature of
the energy landscape in Boltzmann Machines, making it challenging for the
learning algorithm to escape local minima and converge to the global
minimum.

107. STOCHASTIC UPDATE
 Stochastic update refers to the probabilistic updating of neuron states in
Boltzmann Machines
 During each iteration of the learning process, neurons in the Boltzmann
Machine update their states stochastically based on a probabilistic rule such
as Gibbs sampling or Metropolis-Hastings algorithm
 Stochastic update introduces randomness into the learning process, which
helps explore the energy landscape more effectively and escape local
minima

108. SIMULATED ANNEALING
 Simulated Annealing is a probabilistic optimization technique inspired by the
process of annealing in metallurgy.
 In Simulated Annealing, the system starts at a high temperature where the
probability of accepting moves that increase the energy (i.e., moving to higher
energy states) is high, allowing the system to explore a wide range of states.
 As the optimization process progresses, the temperature is gradually decreased,
reducing the probability of accepting moves that increase the energy. This allows
the system to converge towards the global minimum of the energy landscape while
avoiding getting trapped in local minima.
 Simulated Annealing can be applied to Boltzmann Machines by incorporating
temperature parameters into the stochastic update rule, where the temperature
controls the exploration-exploitation trade-off during the learning process.

109. BOLTZMANN MACHINES USE STOCHASTIC UPDATE RULES TO
EXPLORE THE ENERGY LANDSCAPE, BUT THEY ARE SUSCEPTIBLE
TO THE FALSE MINIMA PROBLEM.
SIMULATED ANNEALING IS A TECHNIQUE THAT CAN BE APPLIED
TO BOLTZMANN MACHINES TO MITIGATE THIS ISSUE BY
CONTROLLING THE EXPLORATION-EXPLOITATION TRADE-OFF
DURING THE LEARNING PROCESS.

110. BASIC FUNCTIONAL UNITS OF ANN FOR PATTERN RECOGNITION TASKS
 Pattern association
 Pattern classification
 Pattern mapping tasks

111. PATTERN ASSOCIATION
 Function: Pattern association tasks involve associating input patterns with
corresponding output patterns. The network learns to produce a specific
output pattern when presented with a corresponding input pattern.
 Illustration: An example of pattern association is associative memory, where
the network learns to recall a stored output pattern when presented with a
similar input pattern. This functionality is often implemented using Hopfield
networks or Content Addressable Memory (CAM) networks.

112. PATTERN CLASSIFICATION
 Function: Pattern classification tasks involve categorizing input patterns into
predefined classes or categories. The network learns to classify input
patterns based on their features or characteristics.
 Illustration: An example of pattern classification is image recognition, where
the network learns to classify images into different classes such as cat, dog,
car, etc. Convolutional Neural Networks (CNNs) are commonly used for
image classification tasks due to their ability to learn hierarchical features.

113. PATTERN MAPPING
 Function: Pattern mapping tasks involve mapping input patterns to specific
output patterns based on a predefined mapping function. The network
learns to transform input patterns into corresponding output patterns.
 Illustration: An example of pattern mapping is function approximation,
where the network learns to approximate a continuous function mapping
input values to output values. This functionality is often implemented using
feedforward neural networks with one or more hidden layers.

114. THANK YOU!
Dr Minakshi Pradeep Atre, PVG’s COET & GKPIM Pune