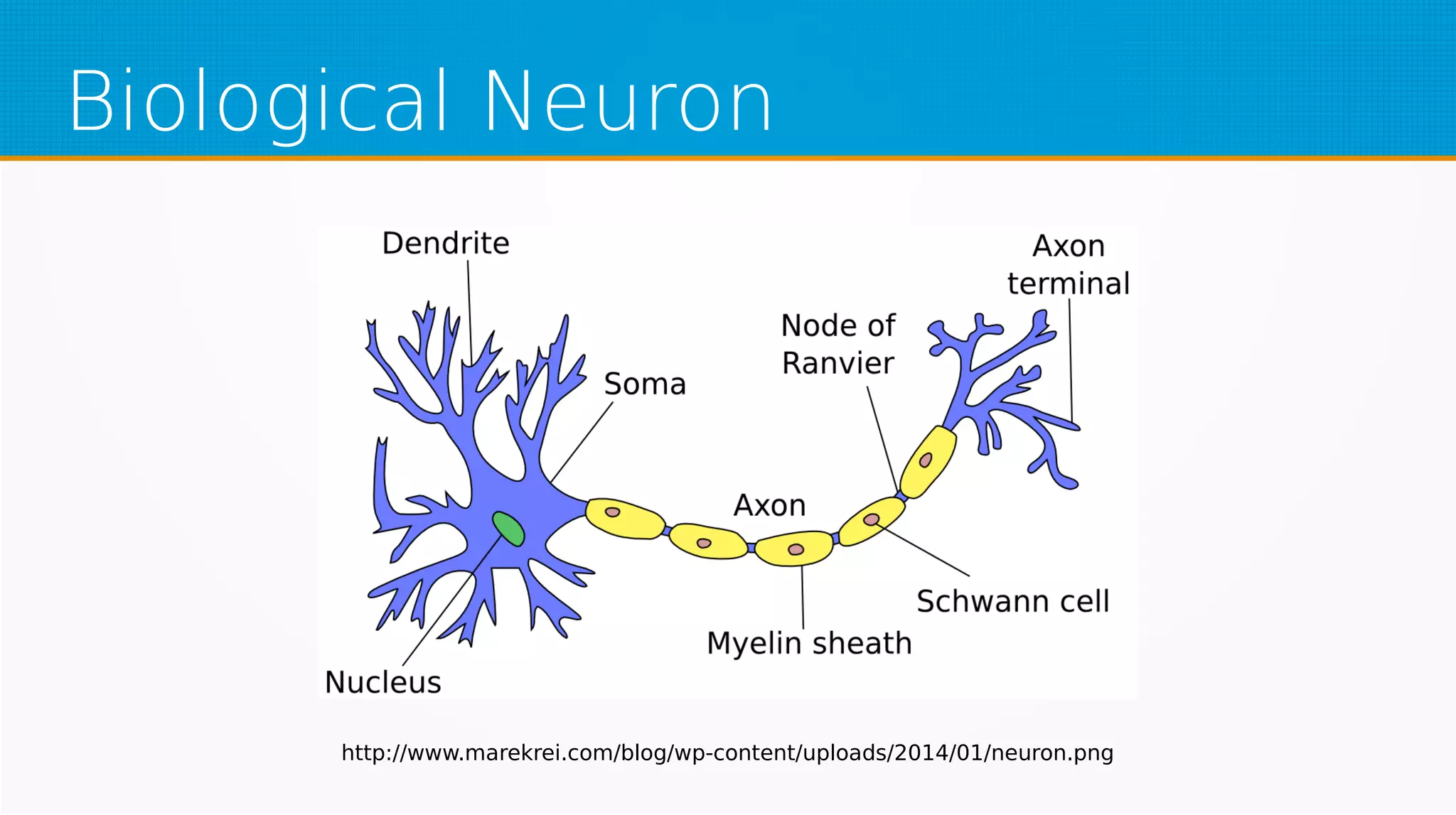
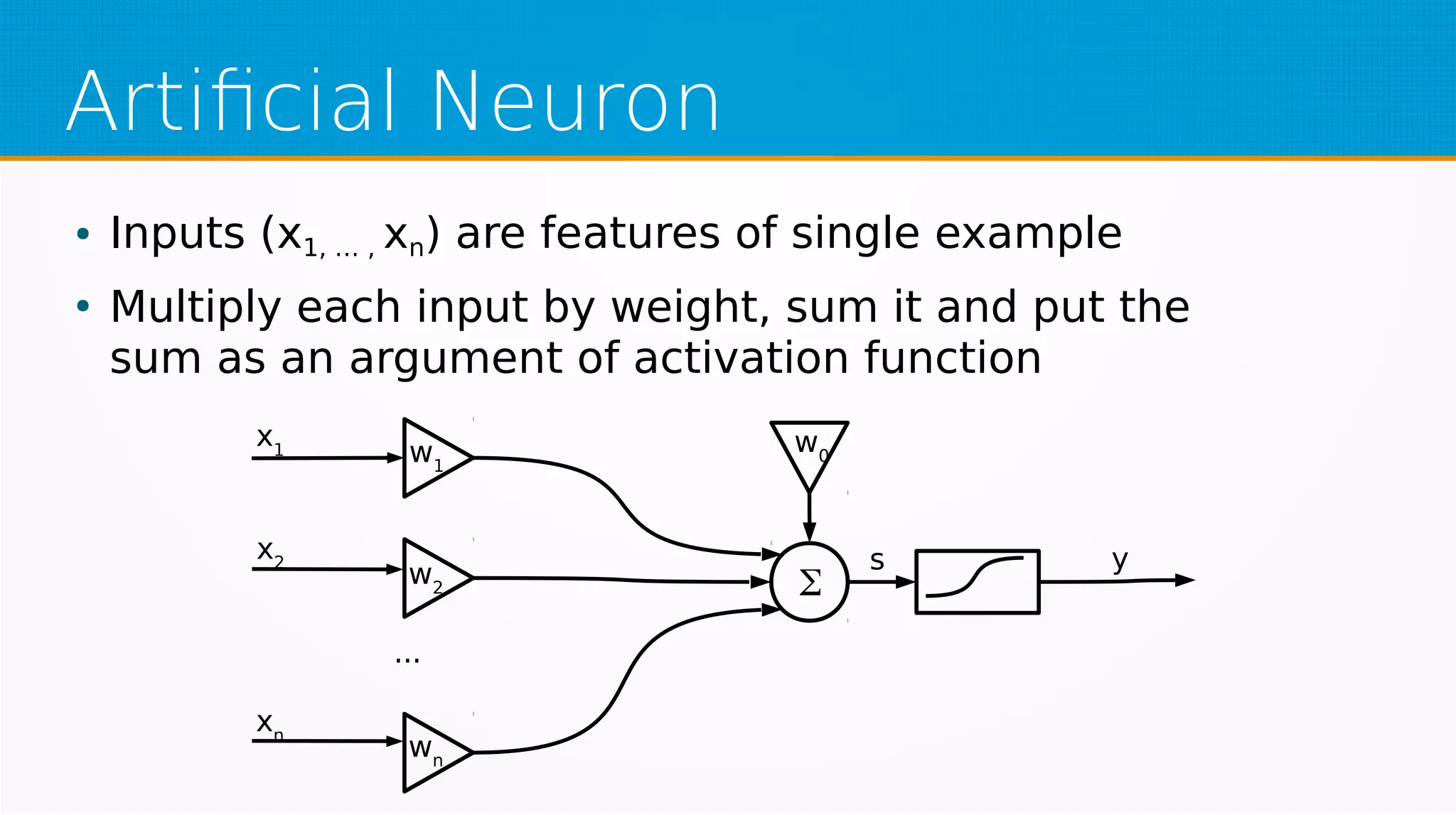
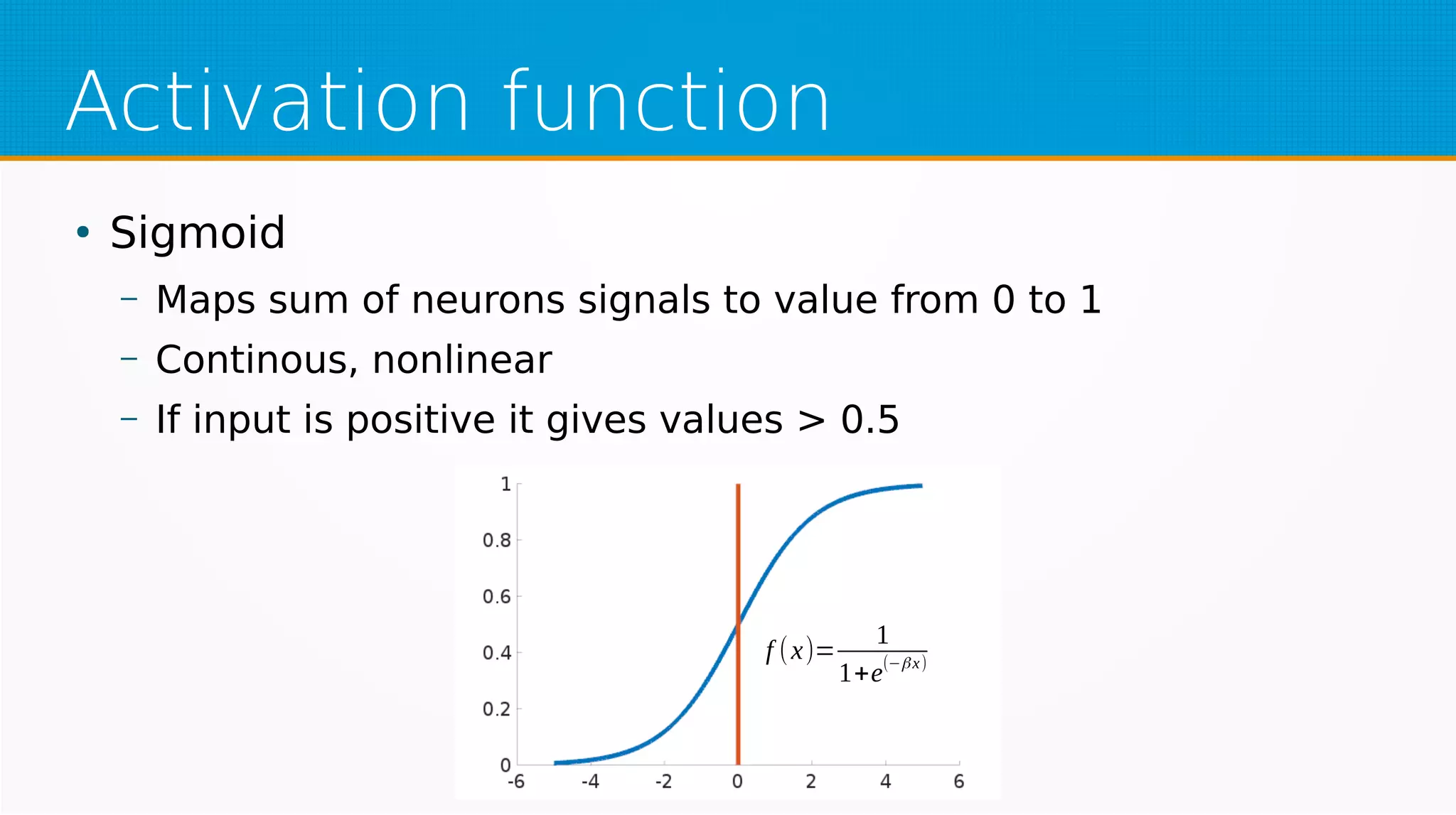
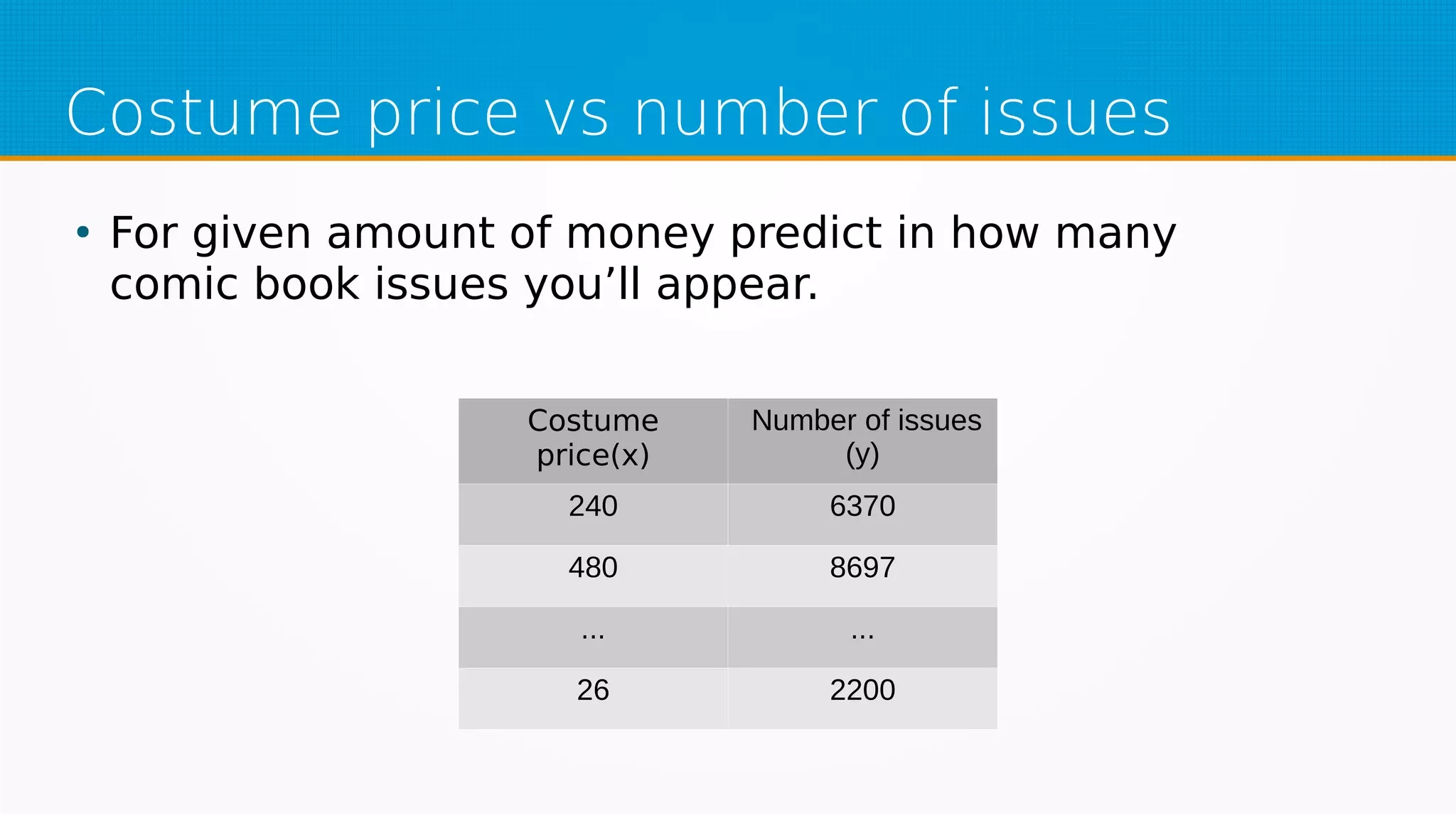
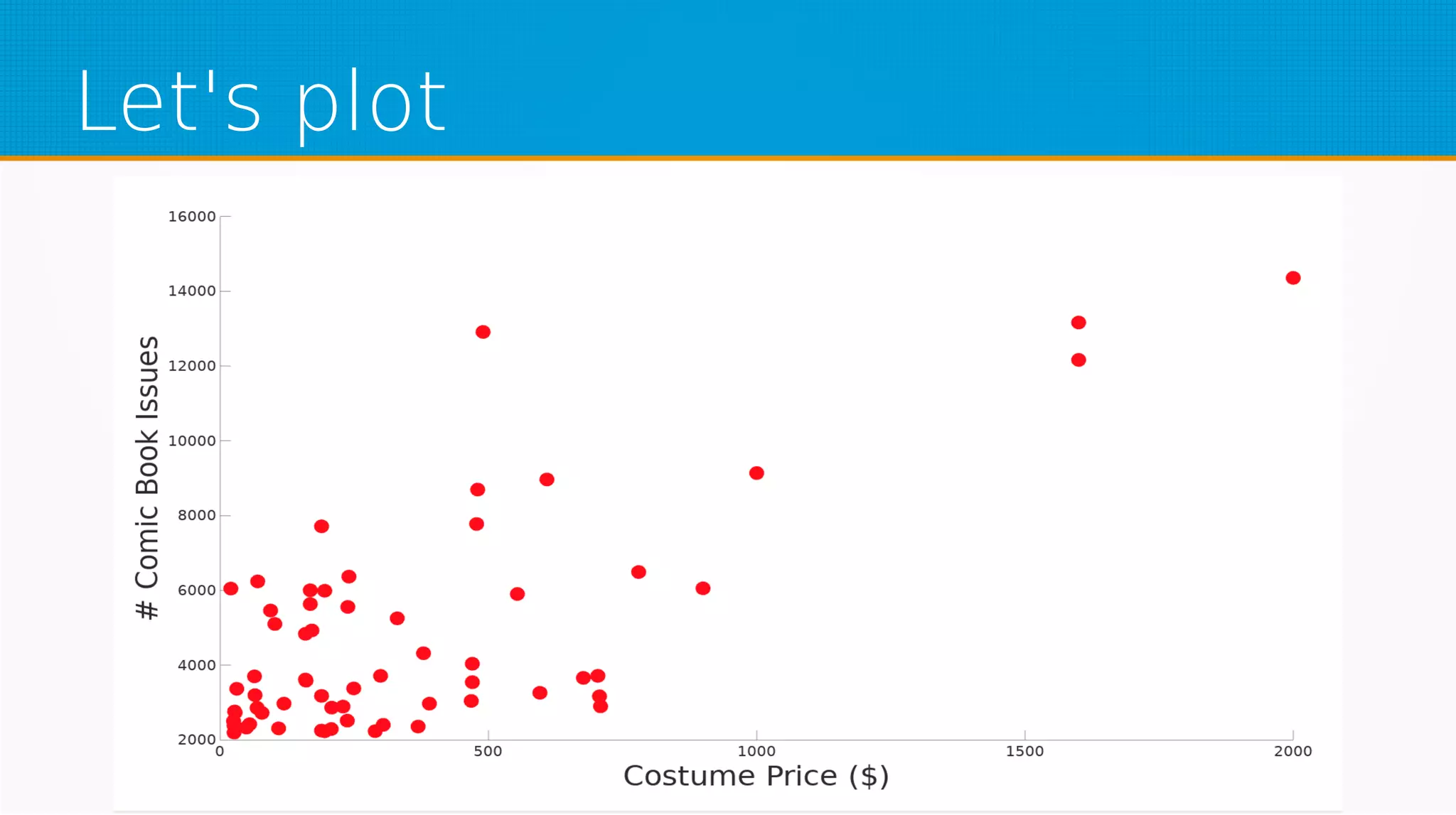
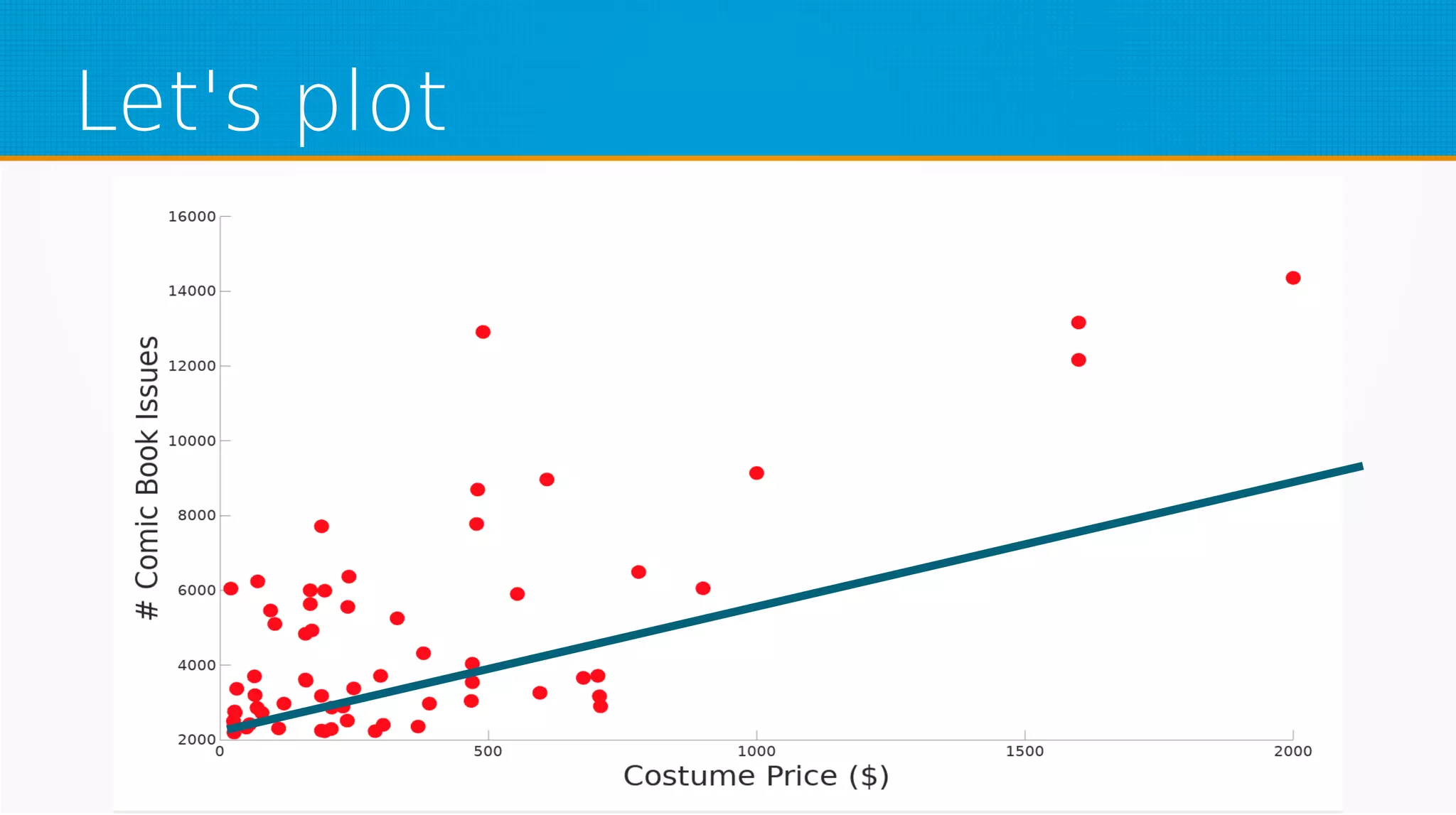
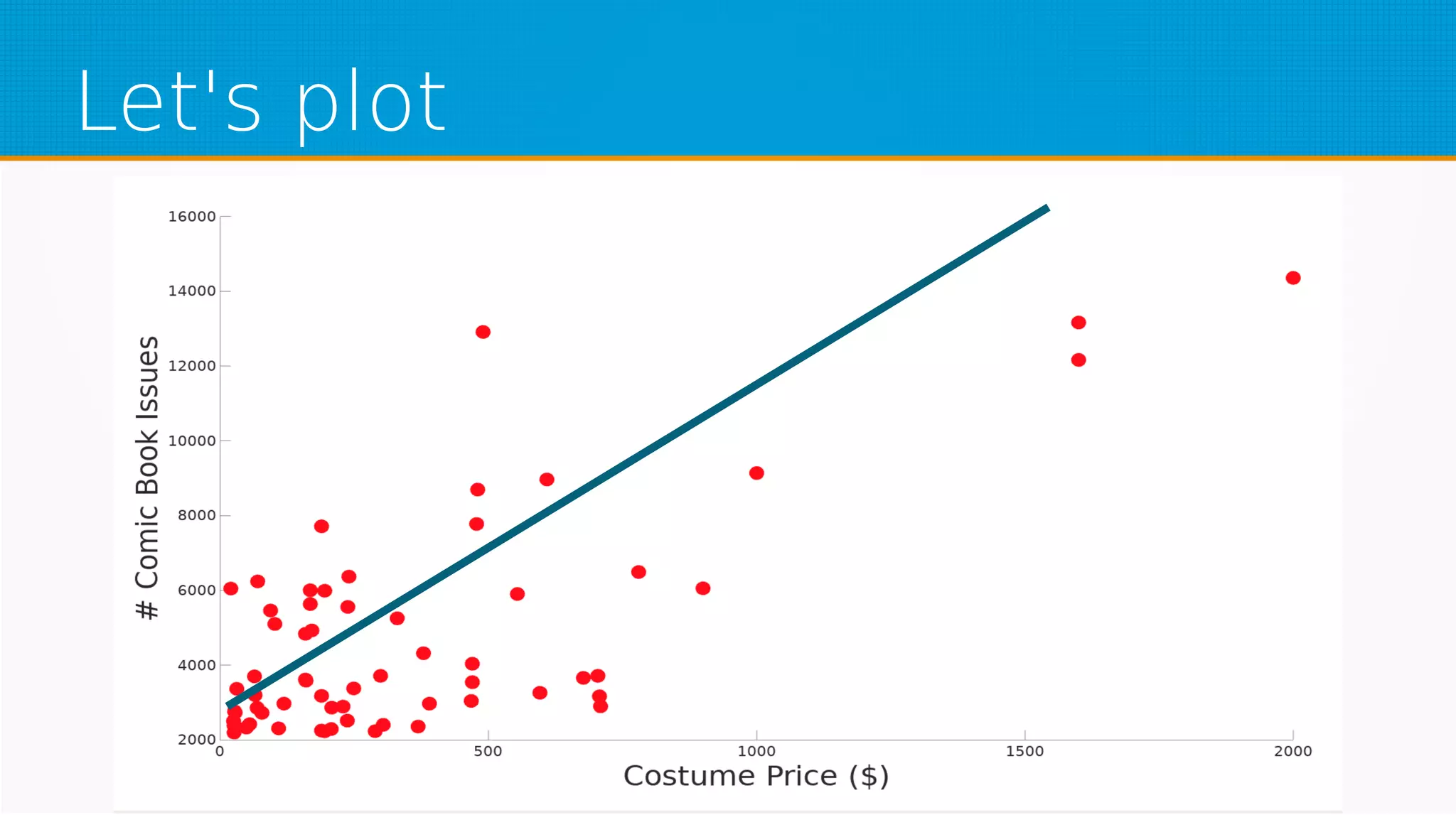
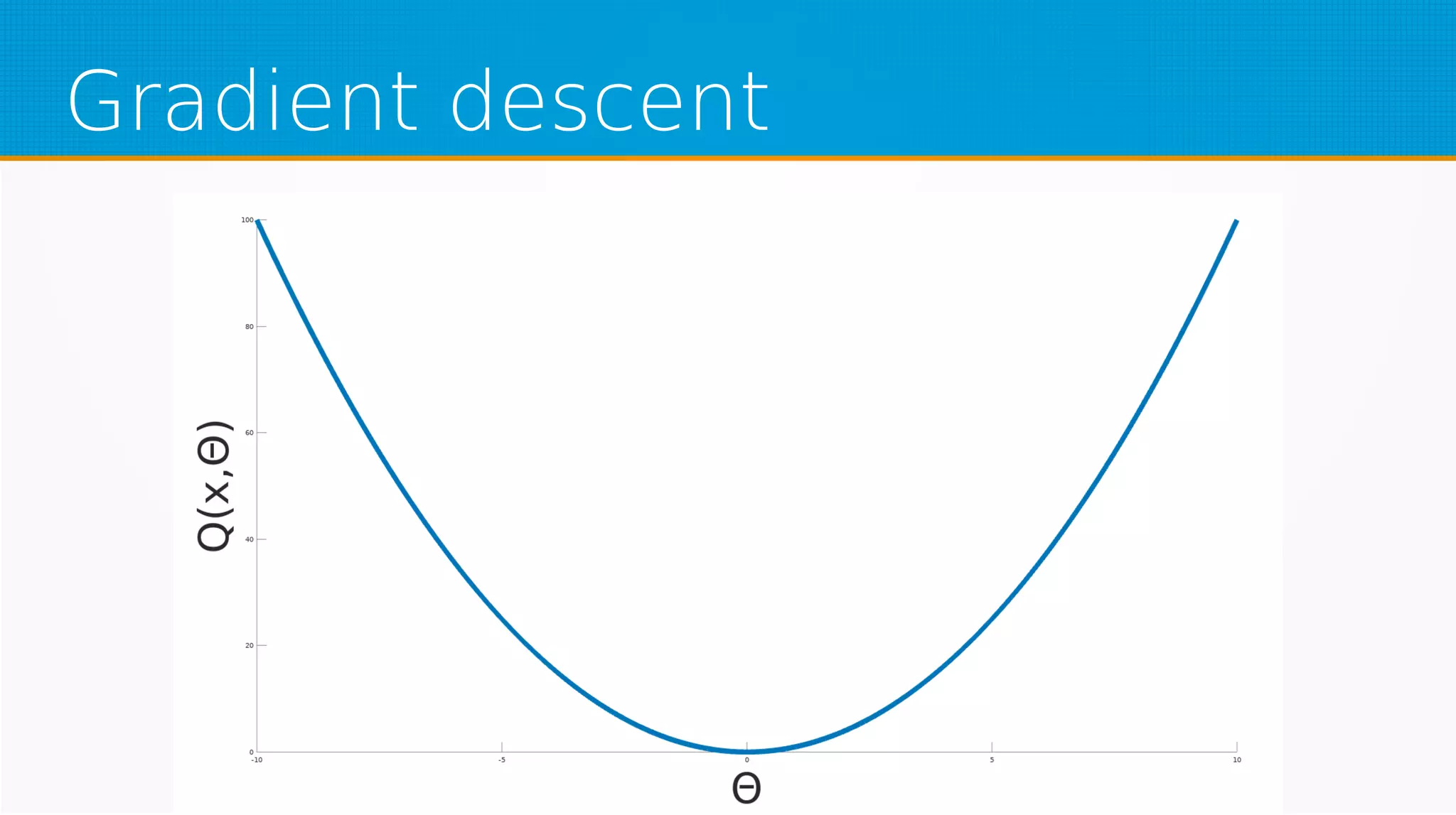
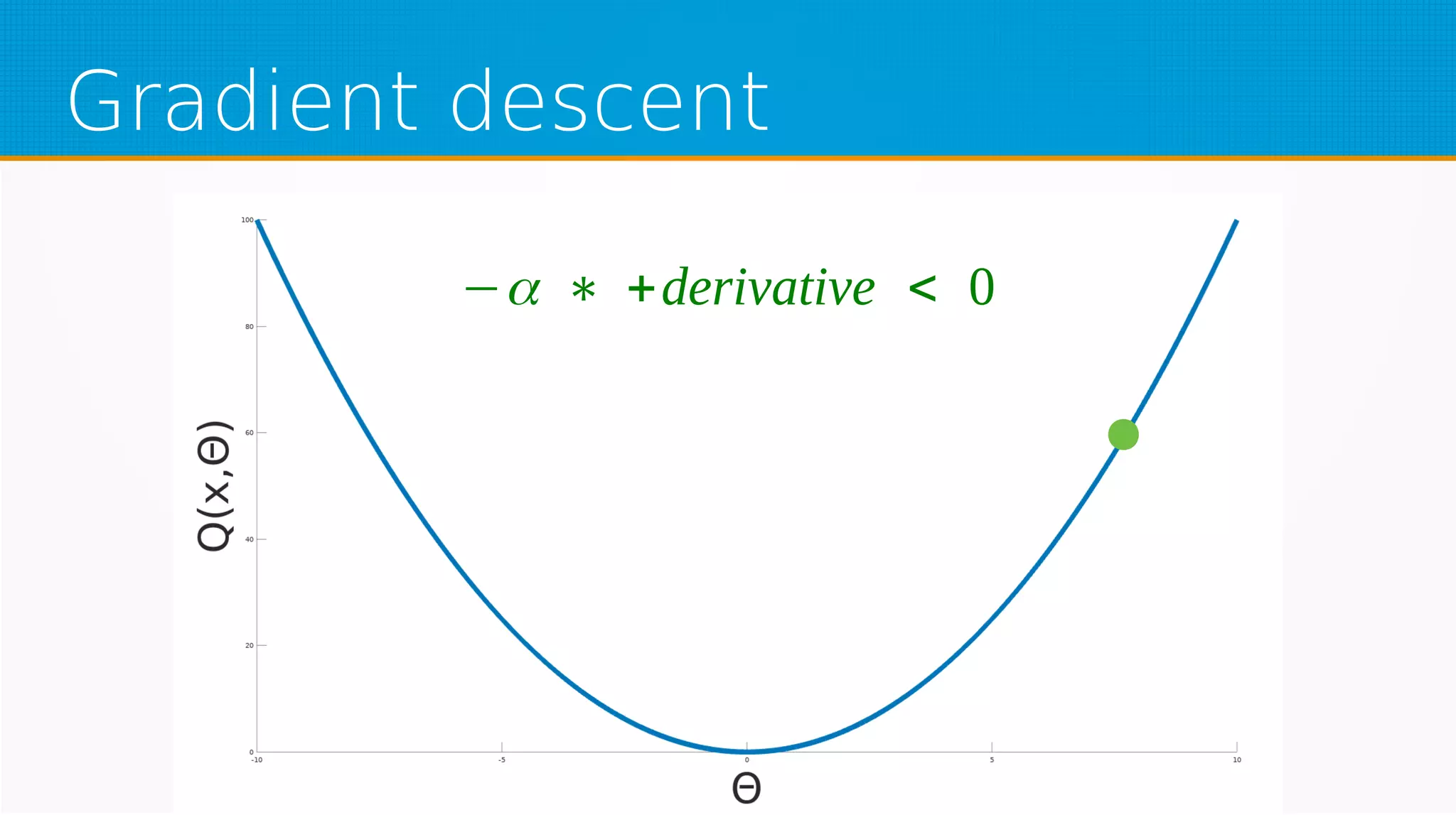
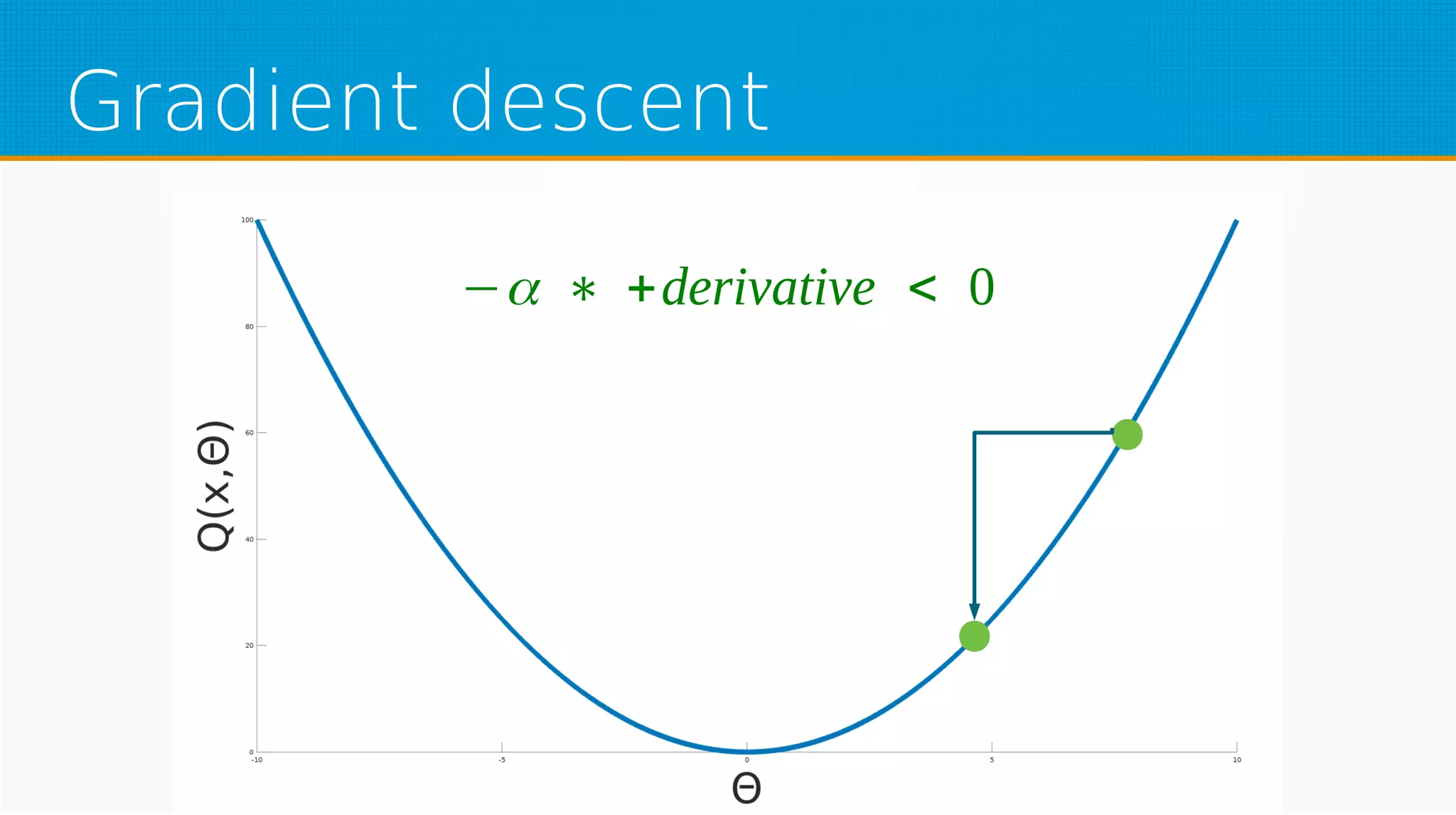
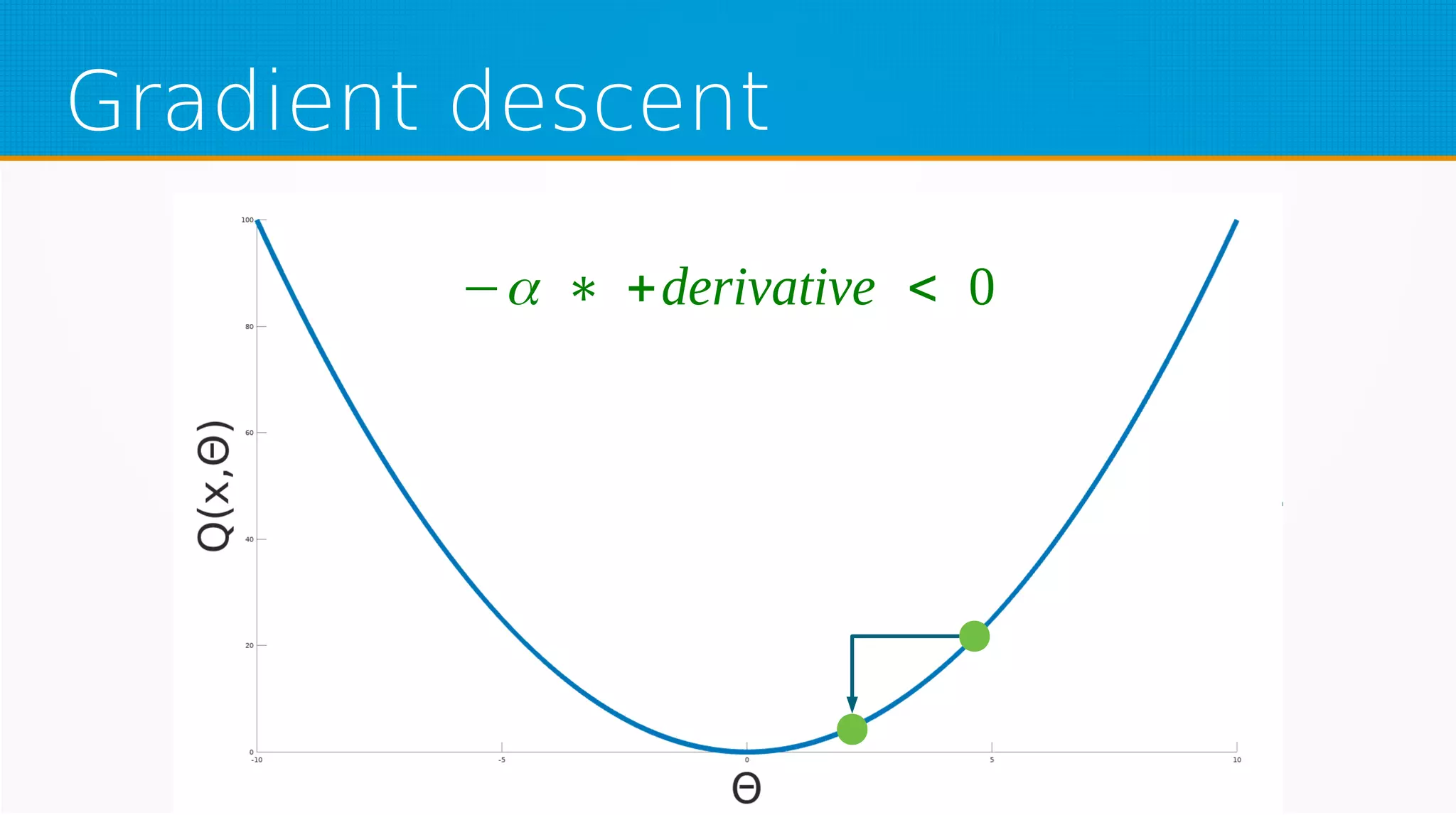
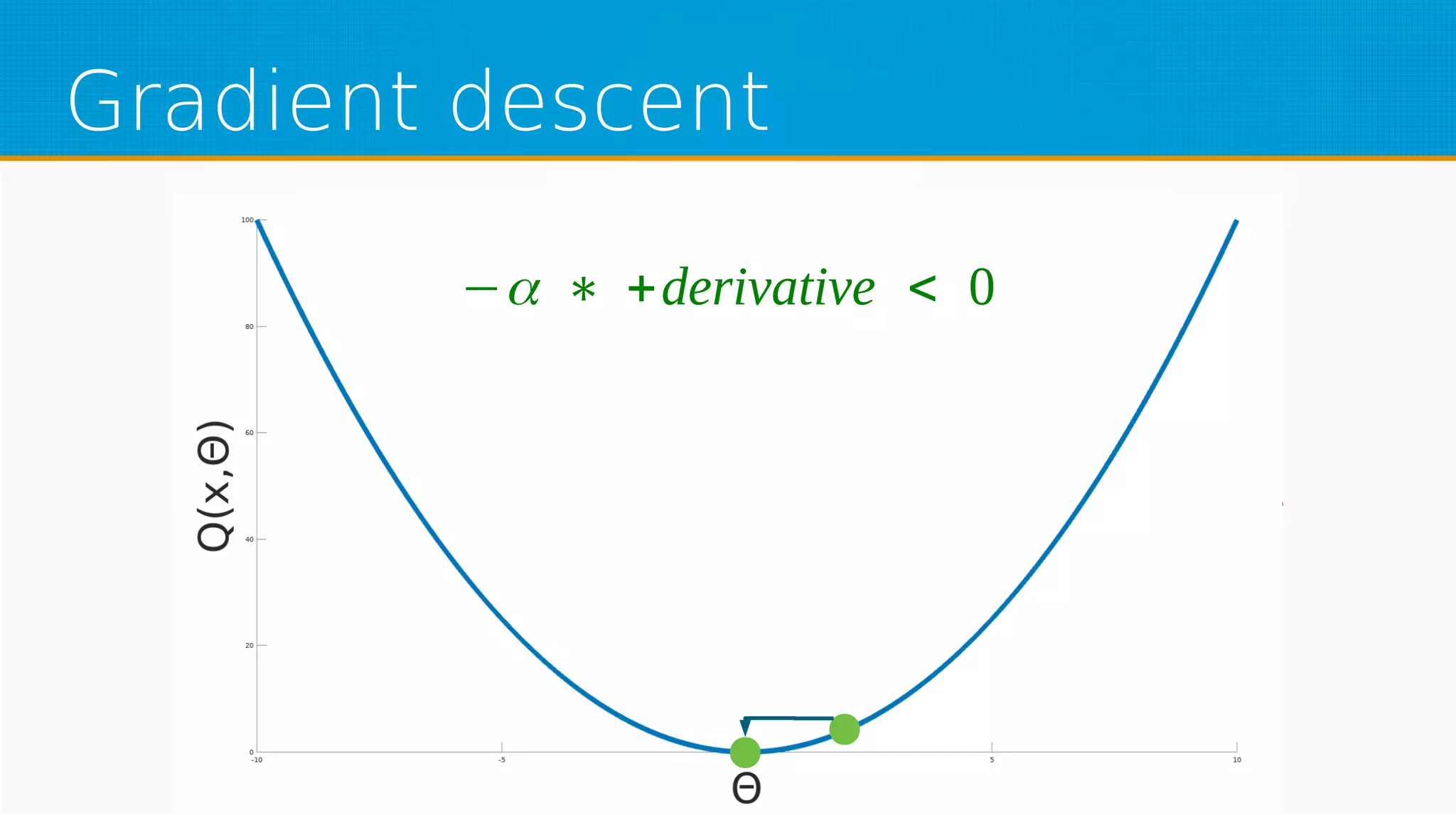
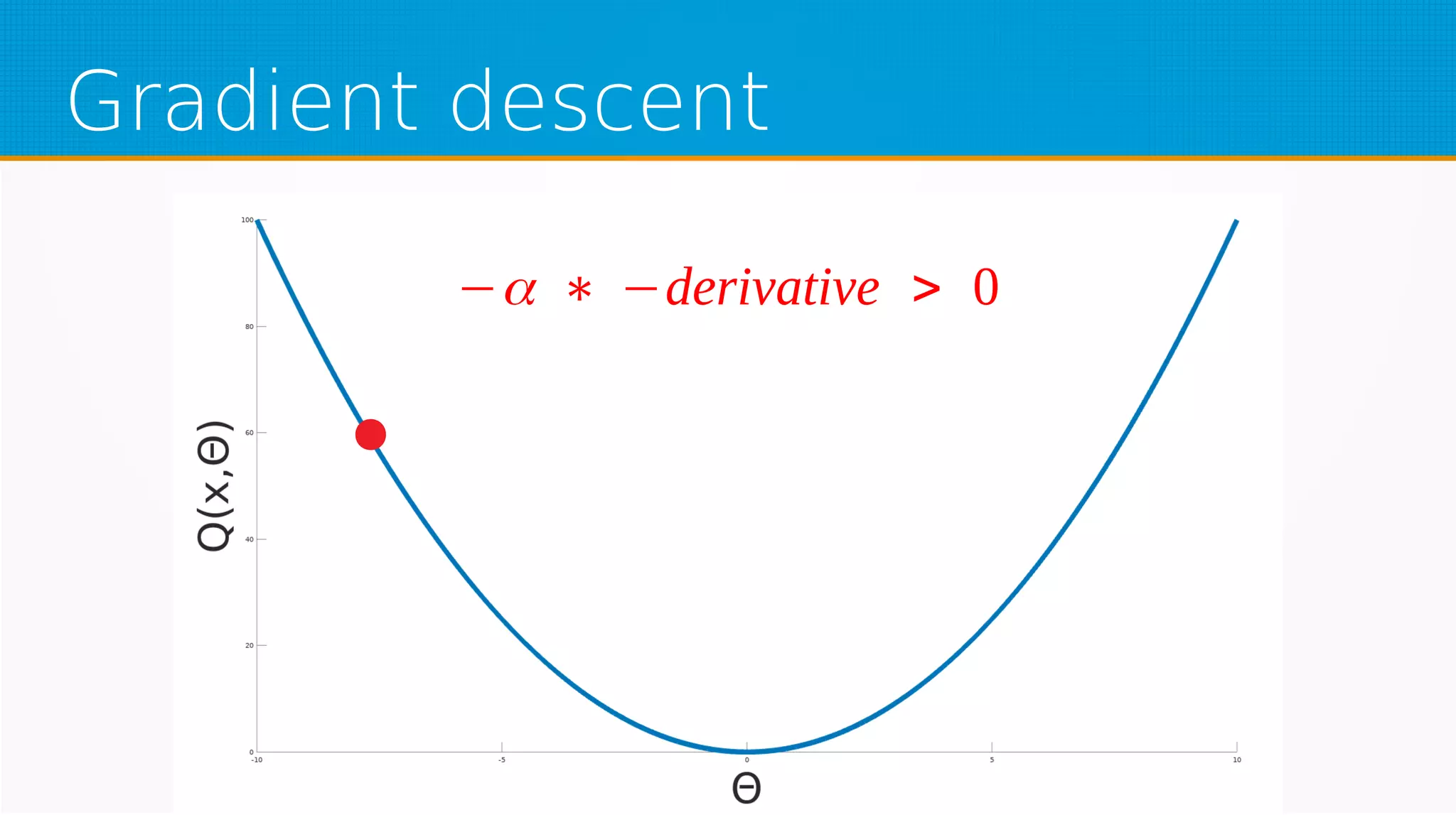
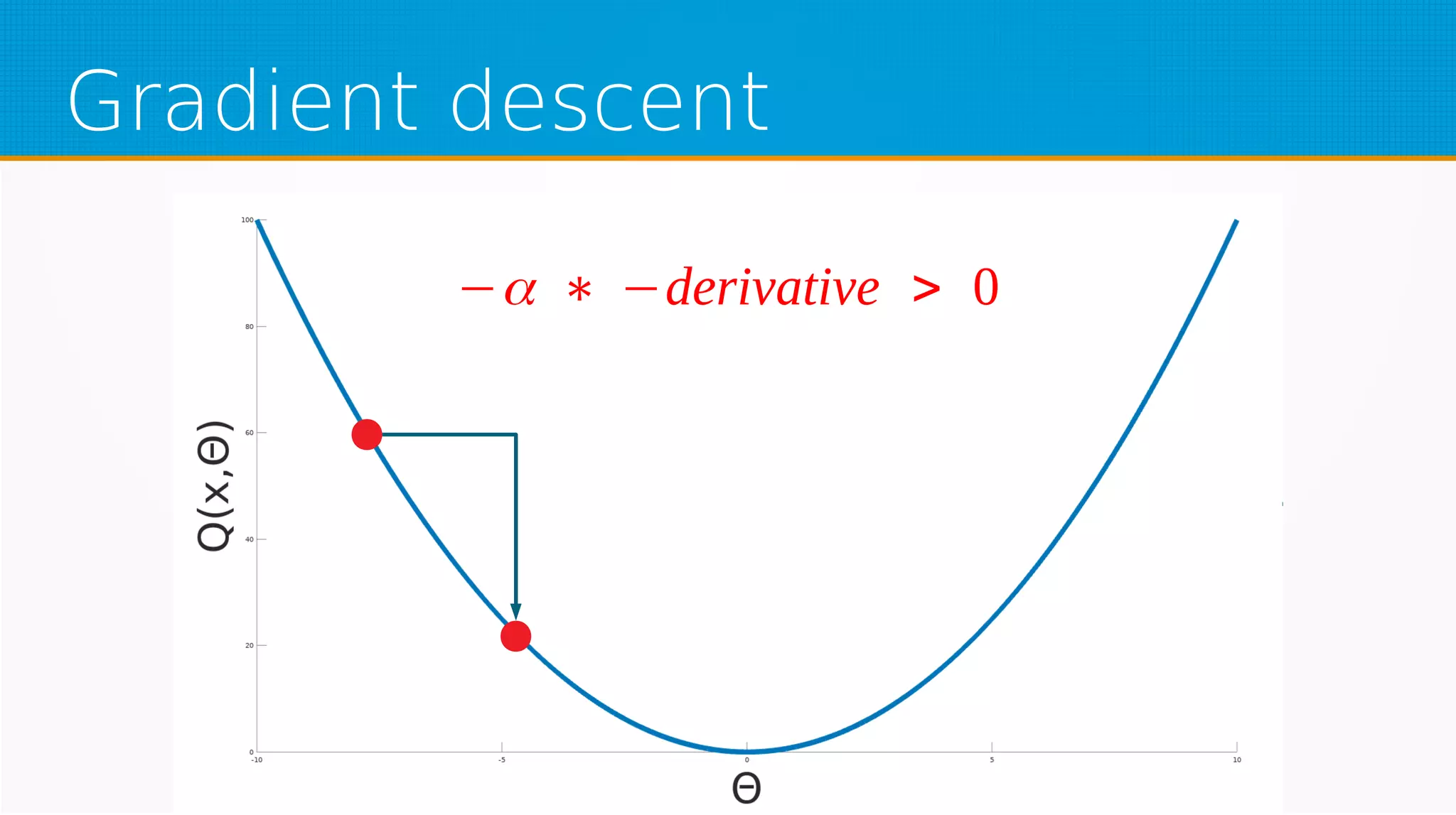
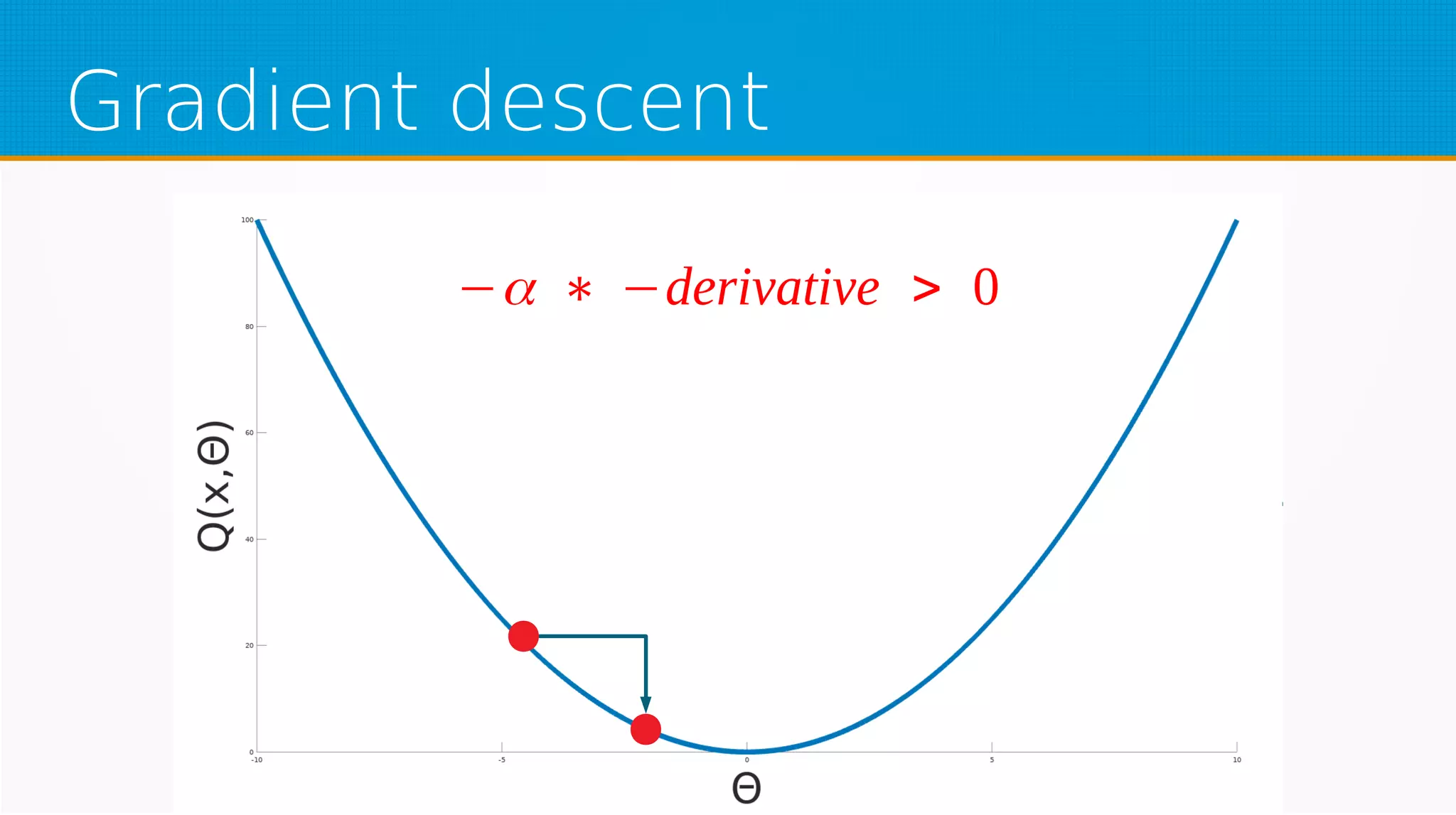
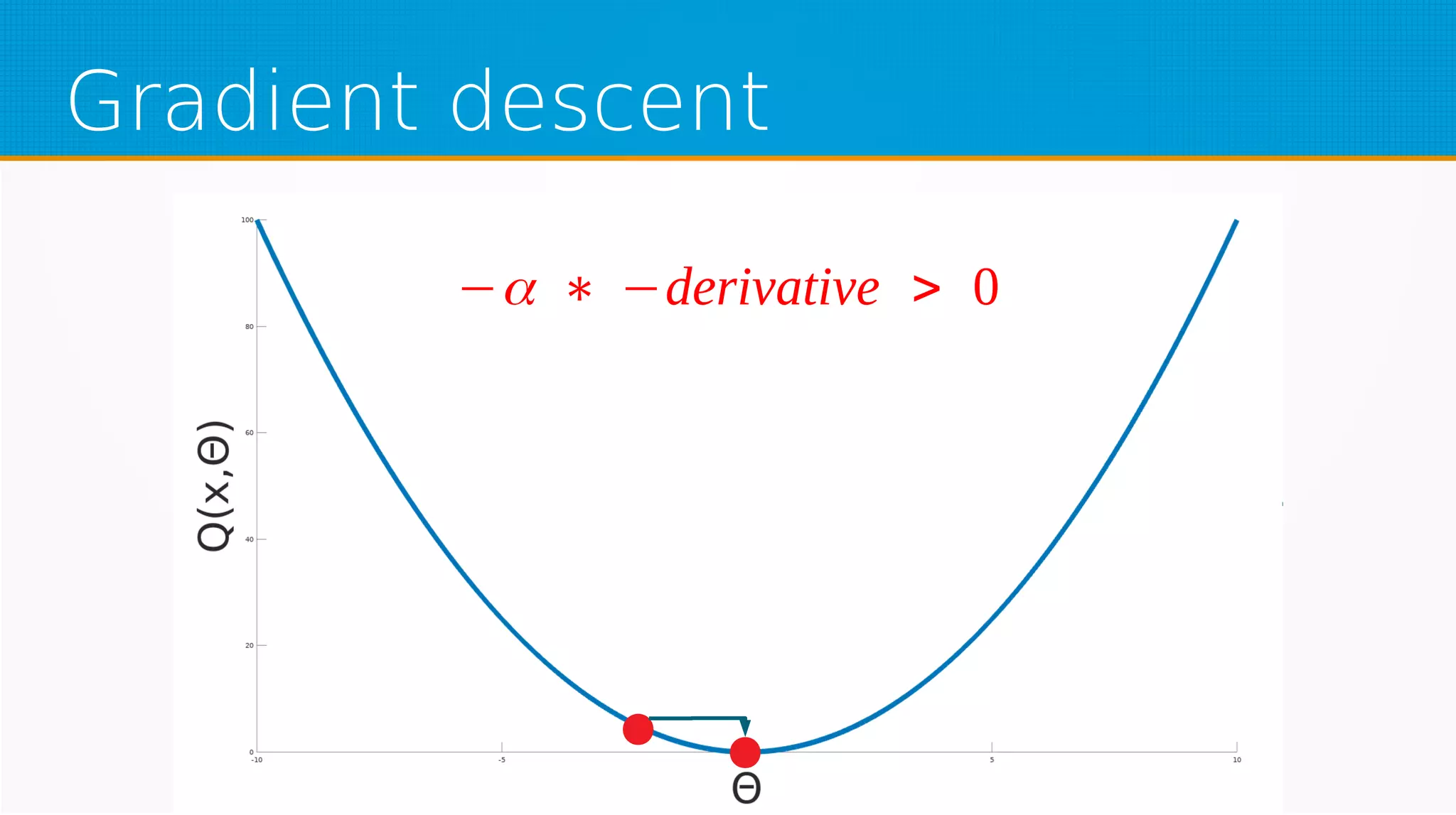
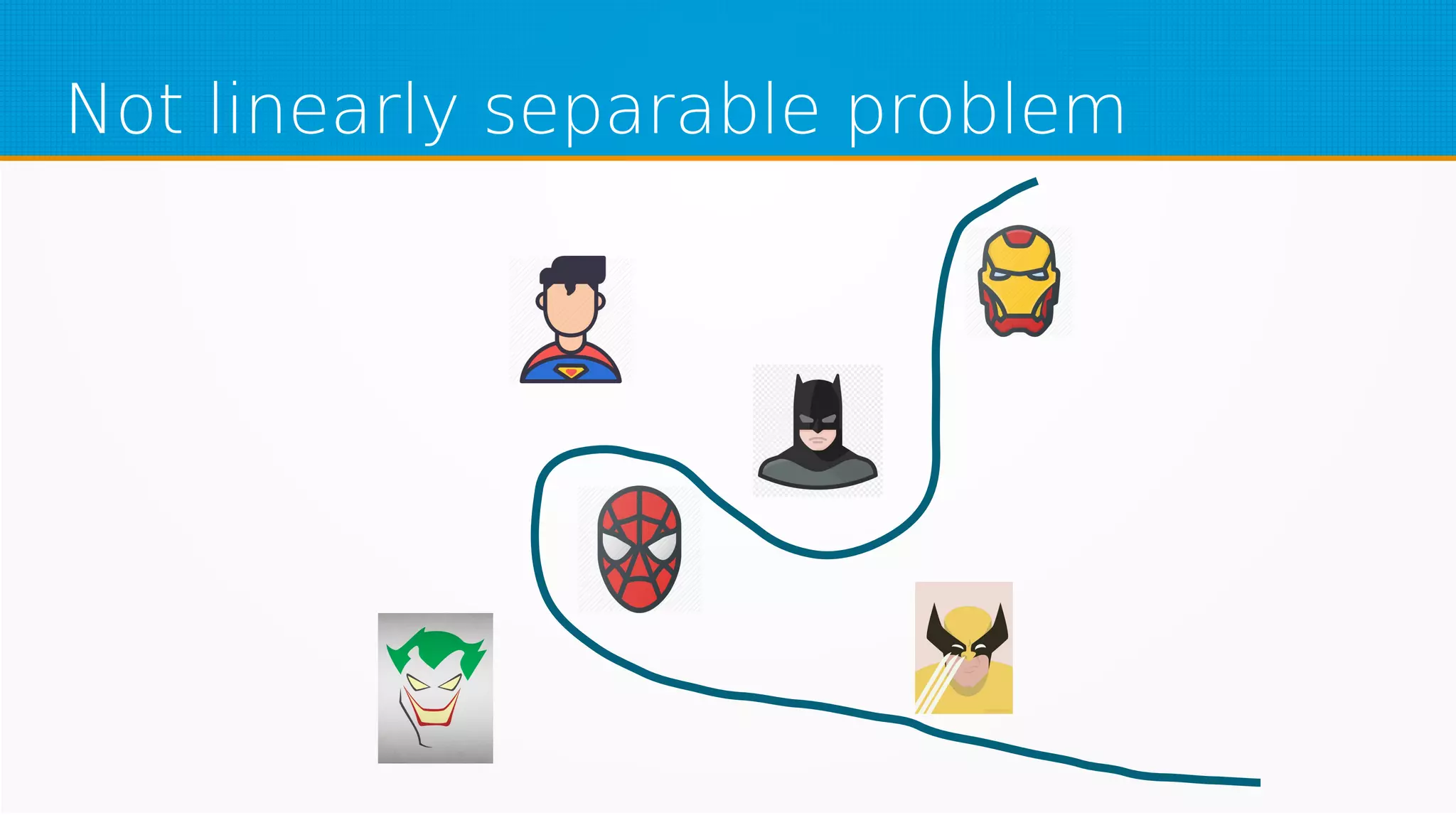
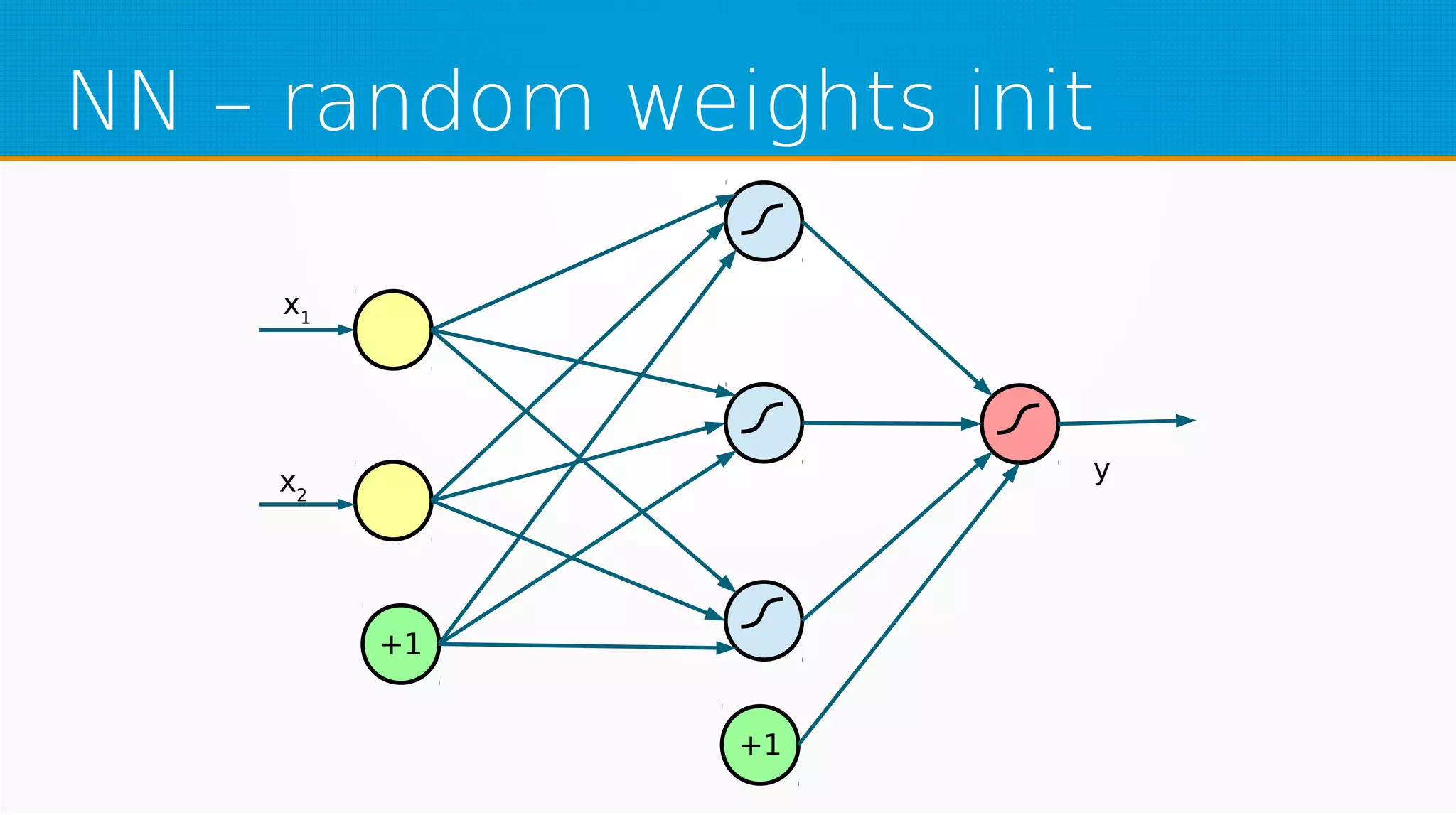
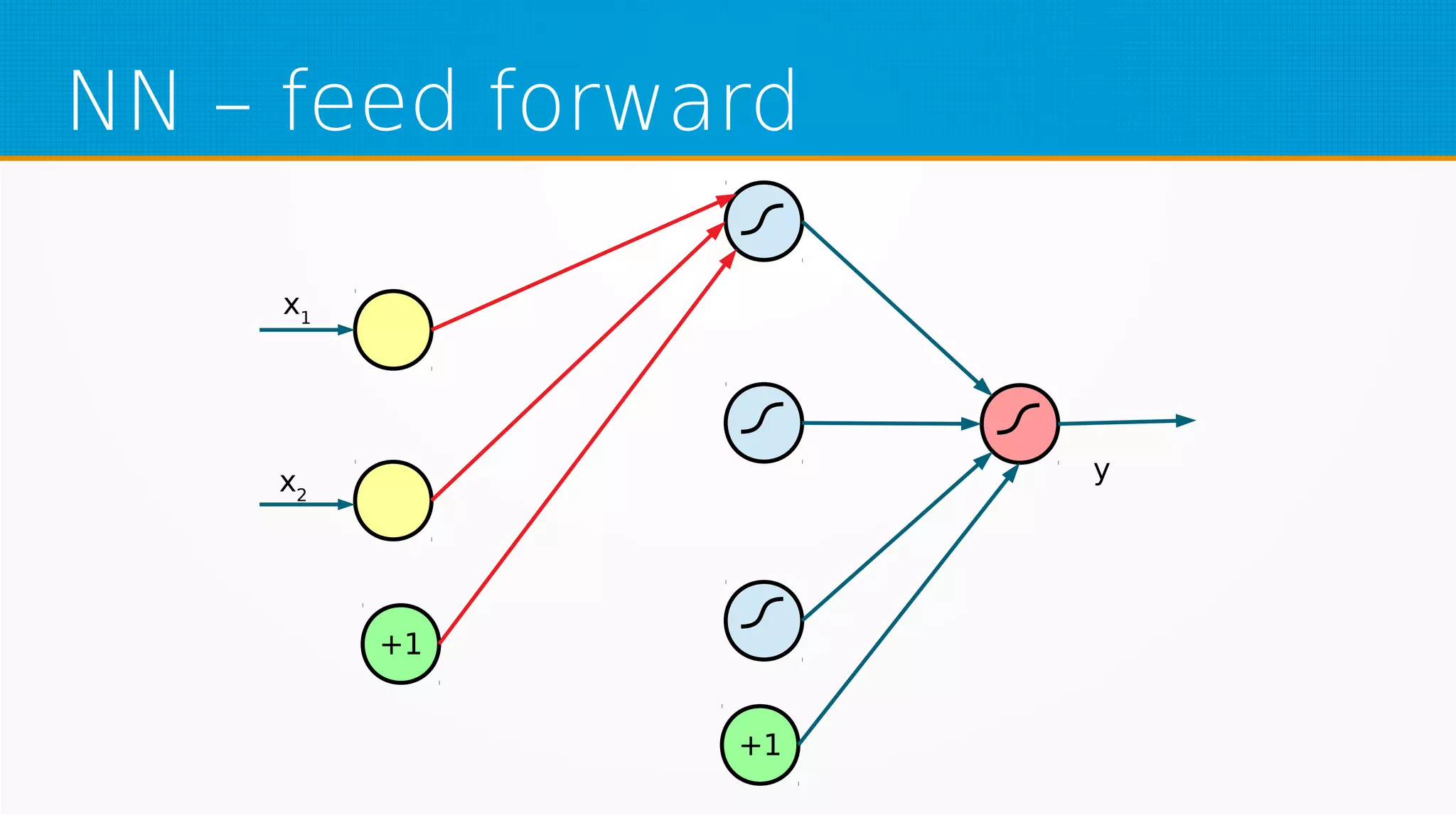
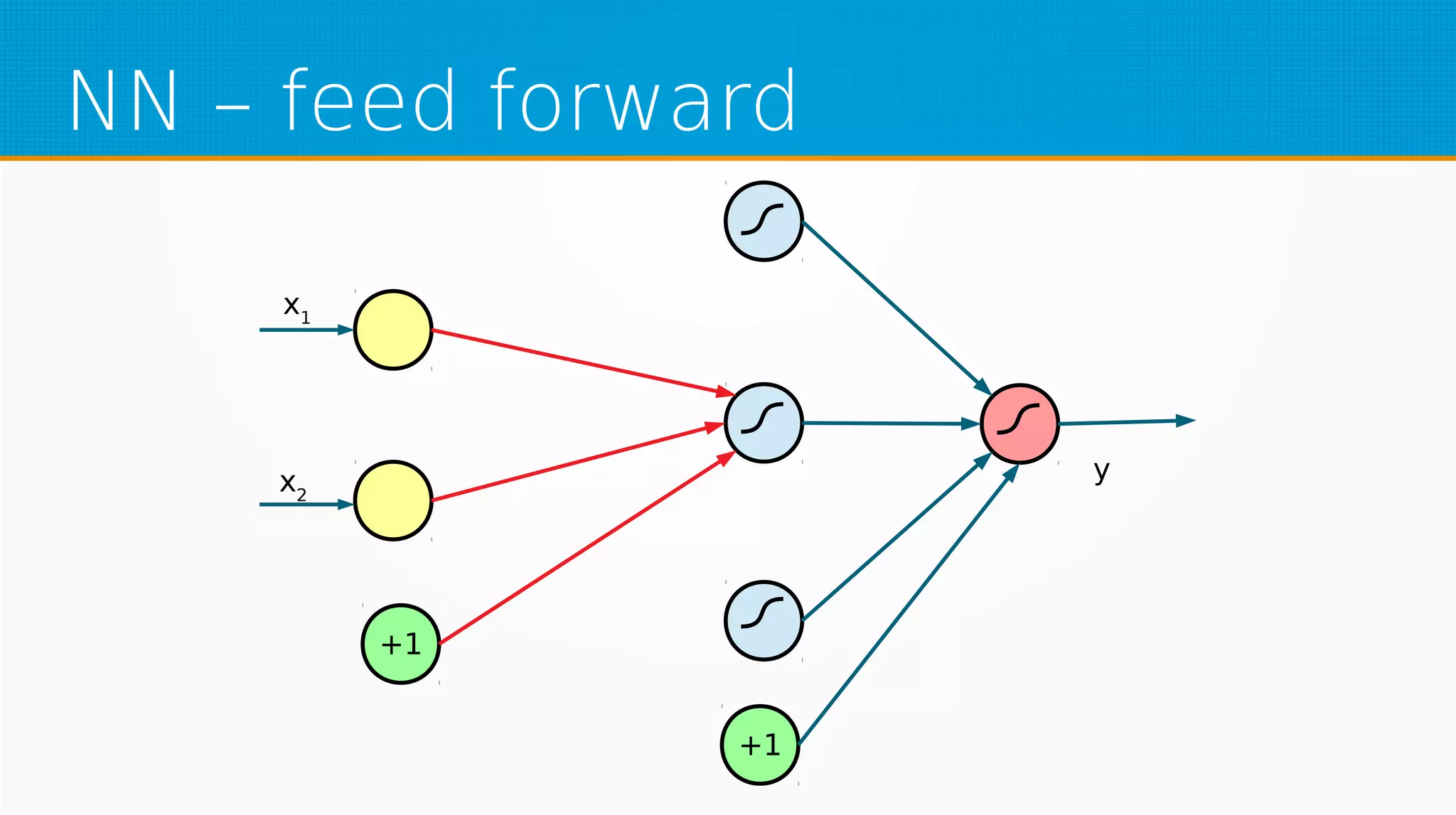
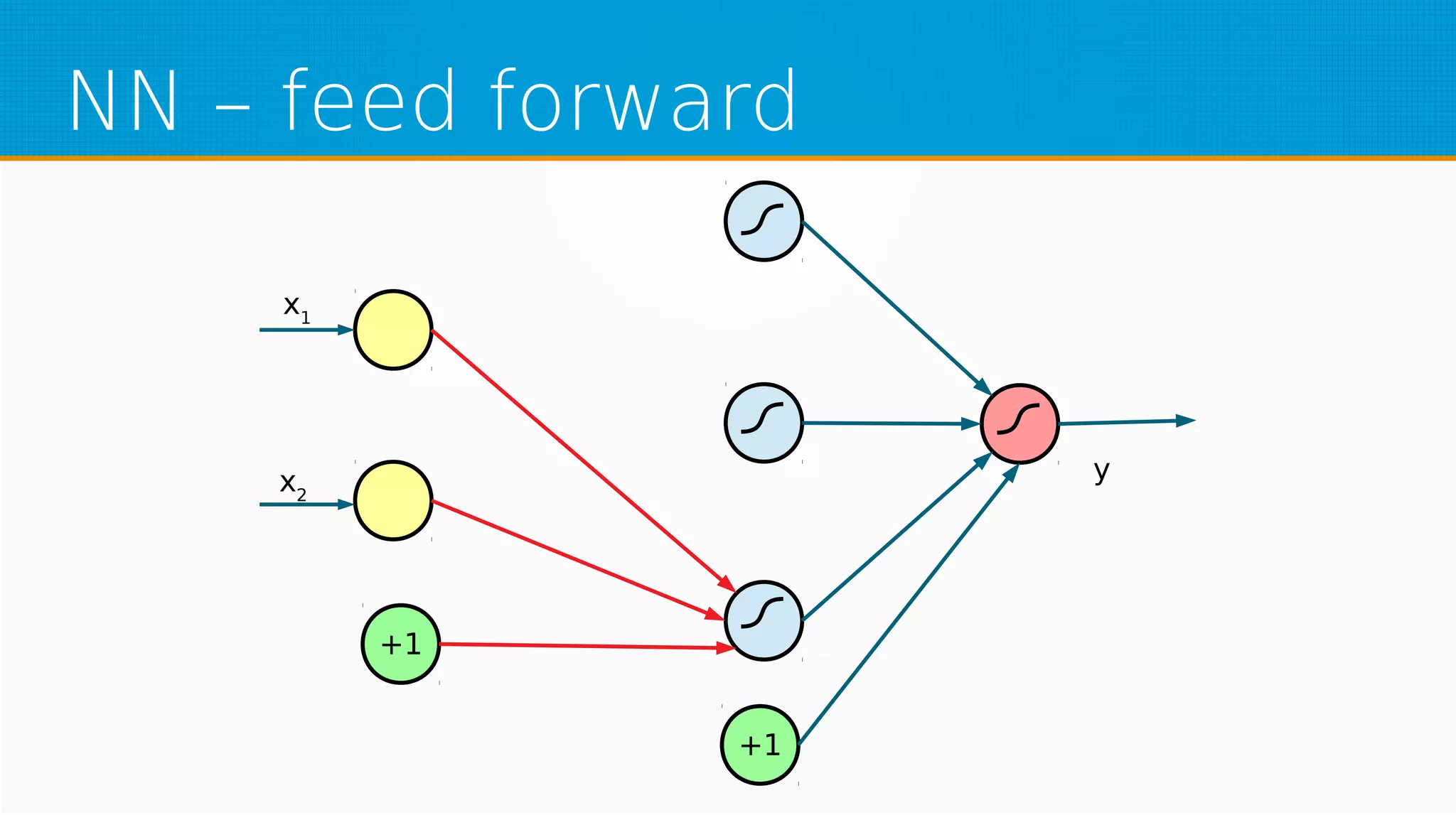
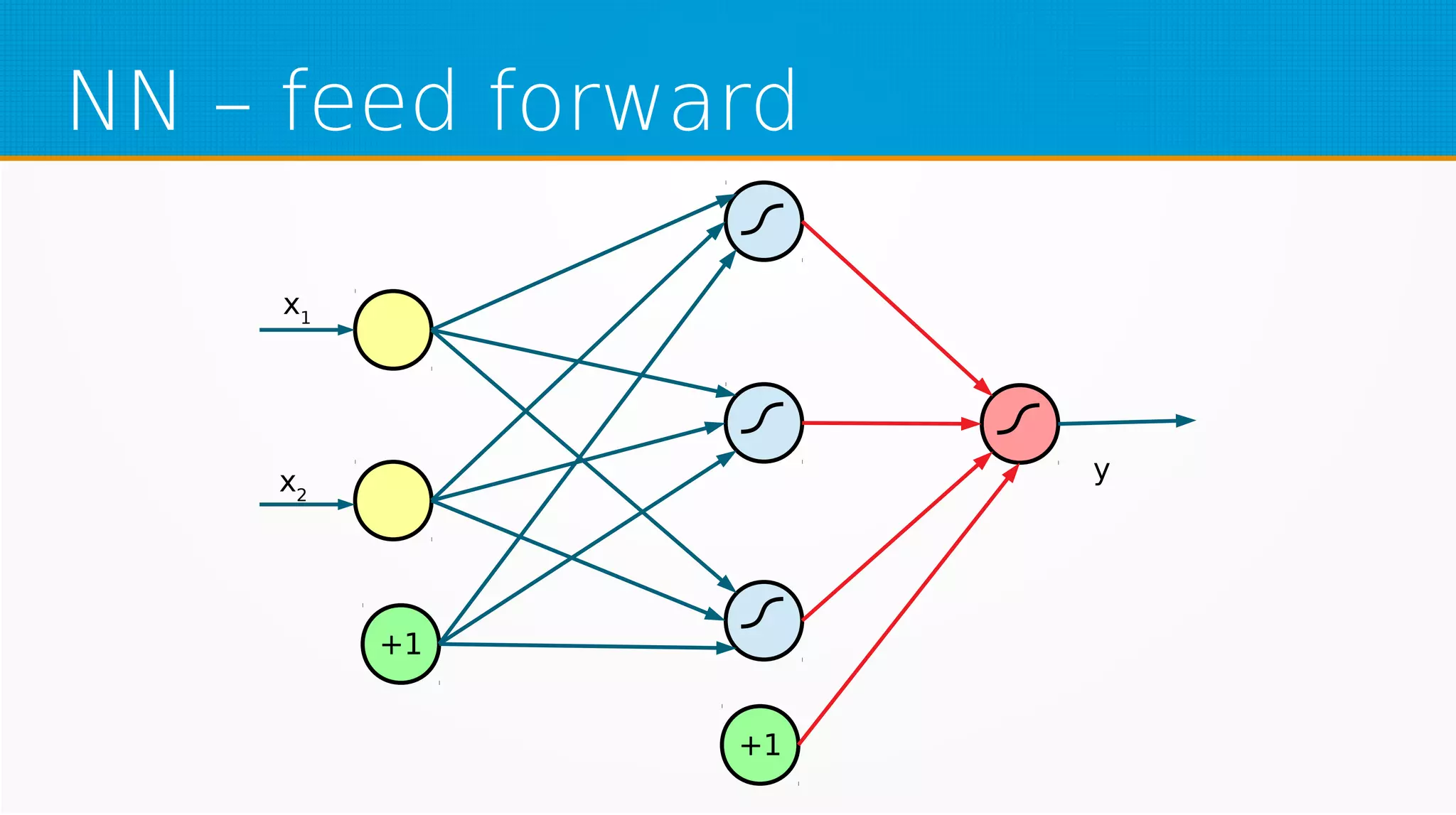
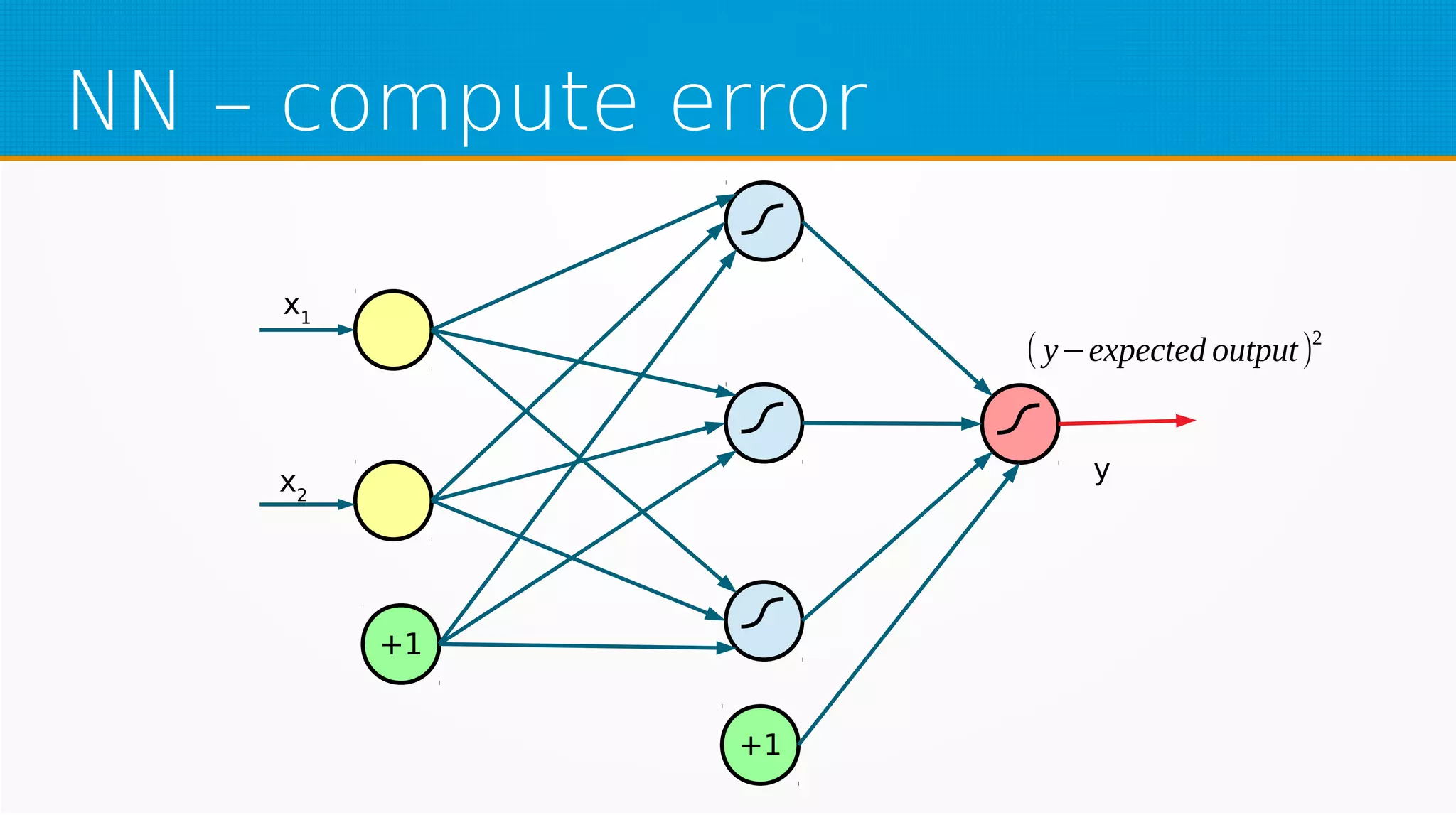
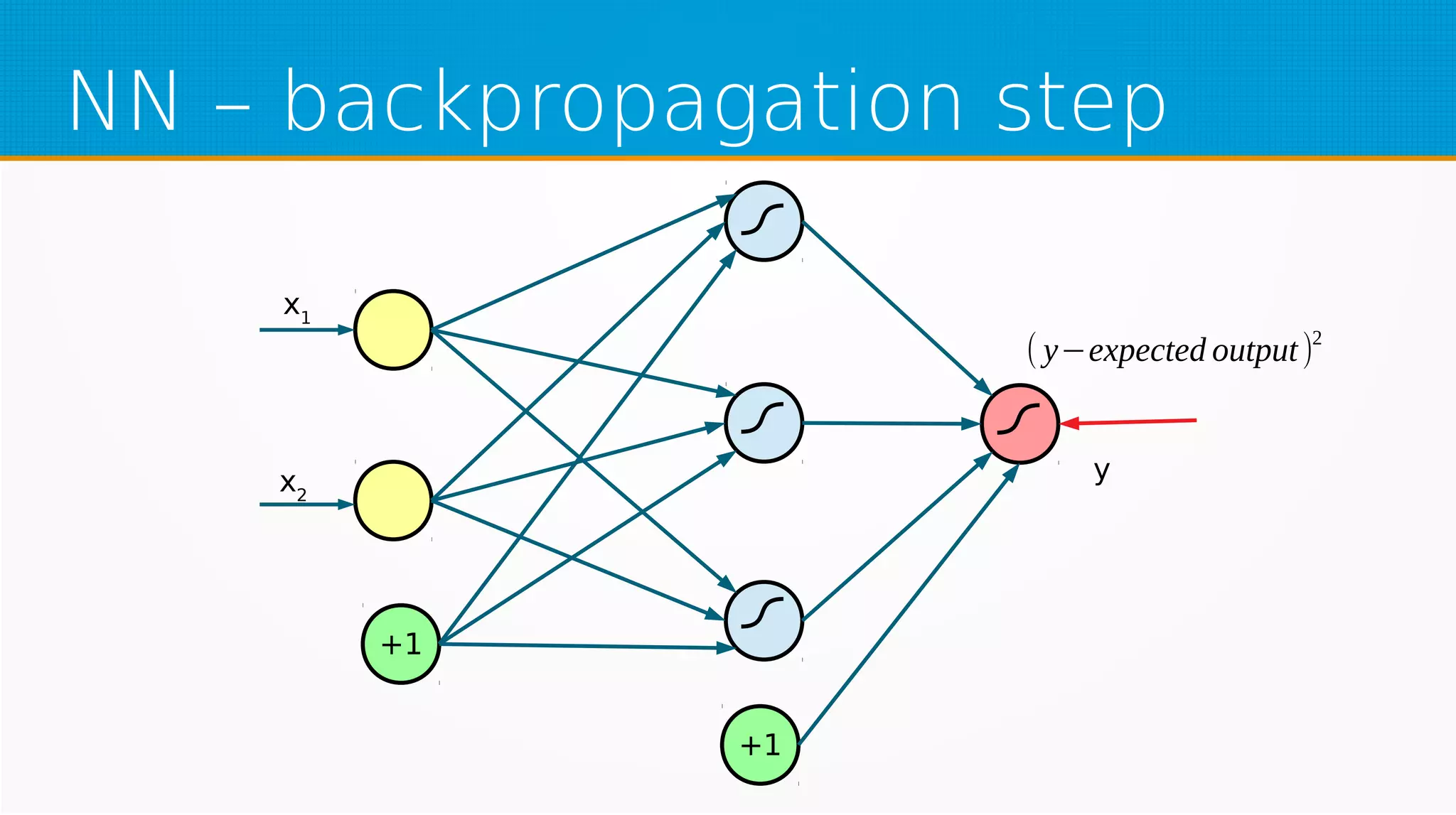
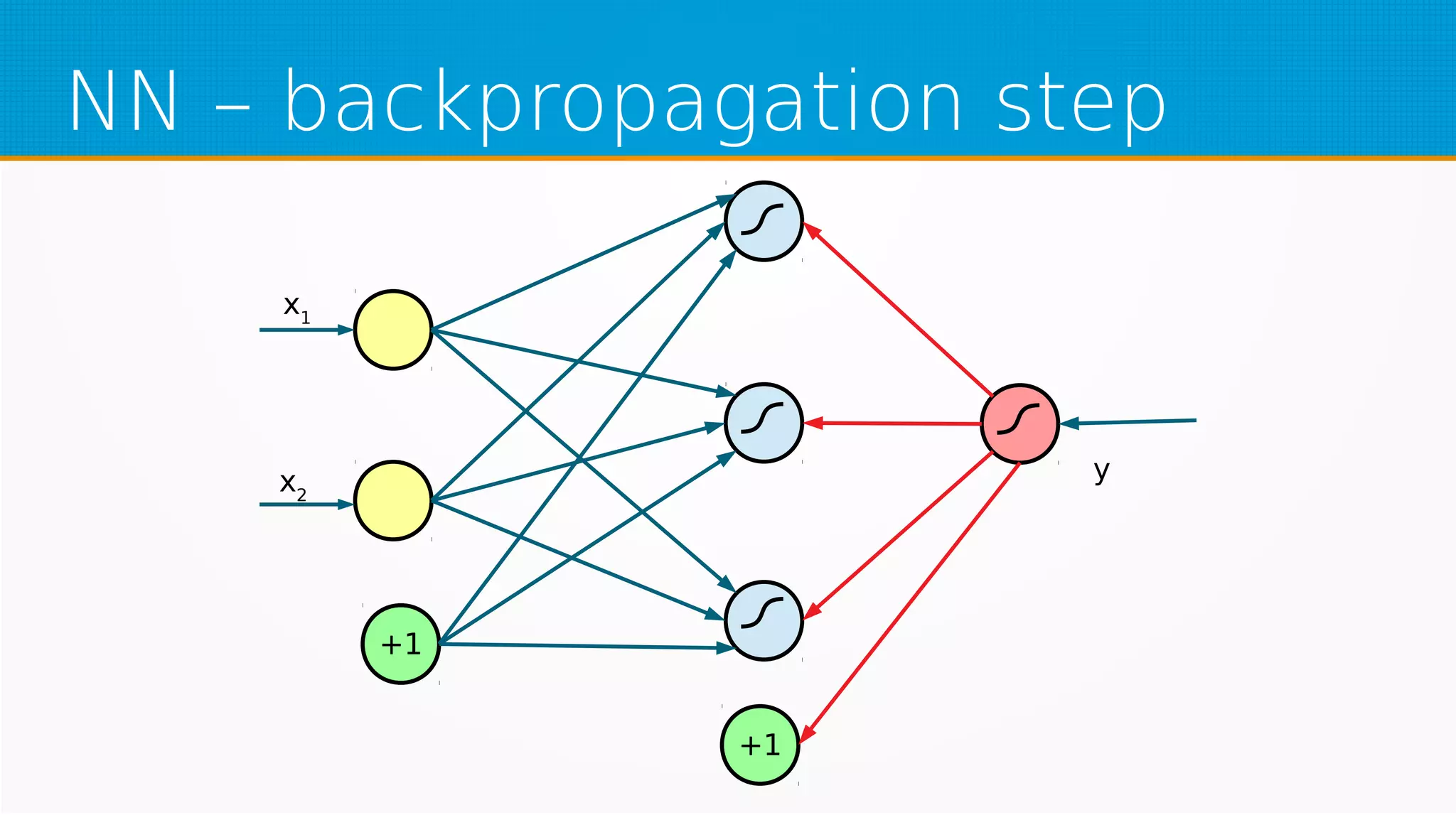
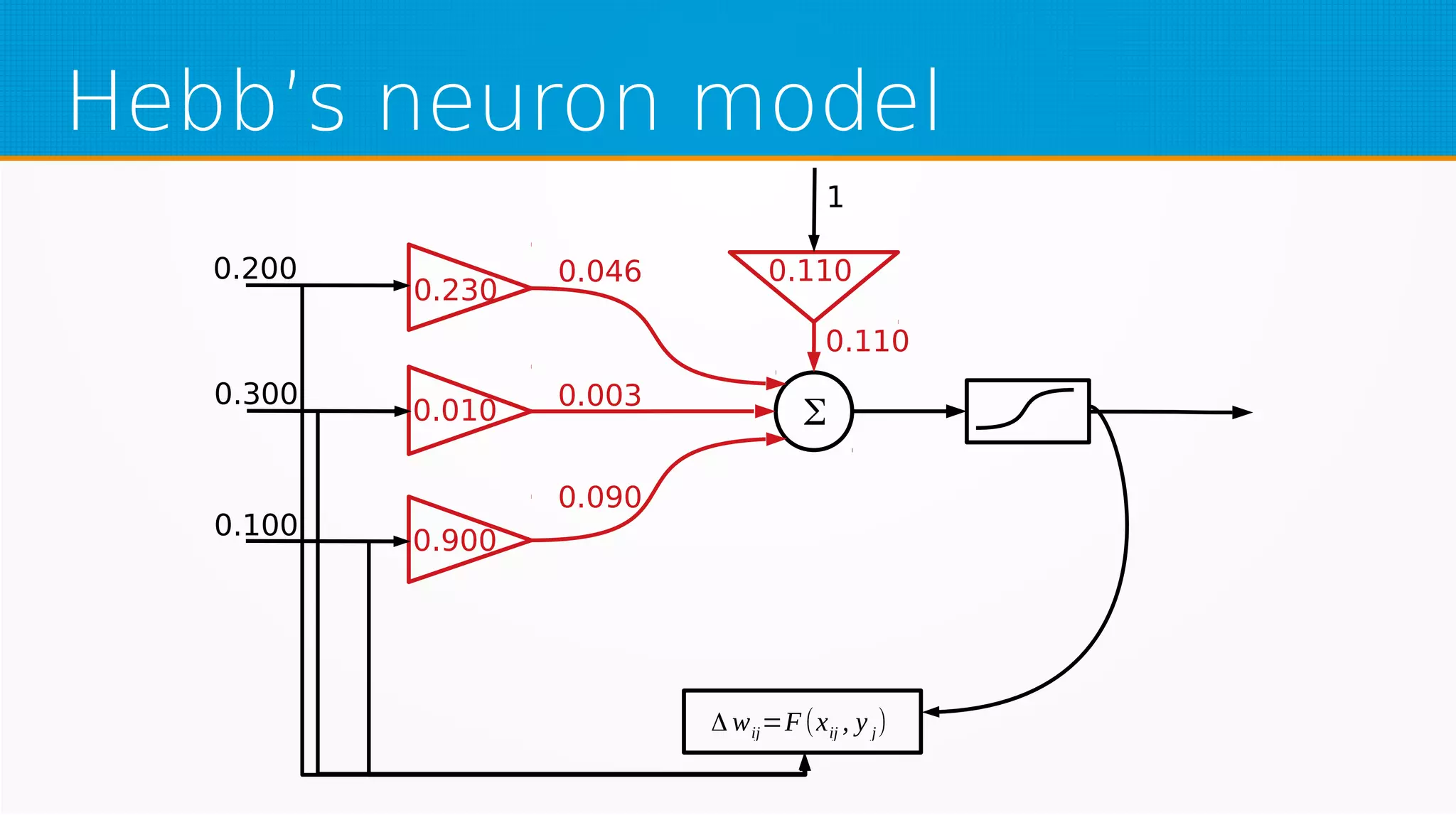
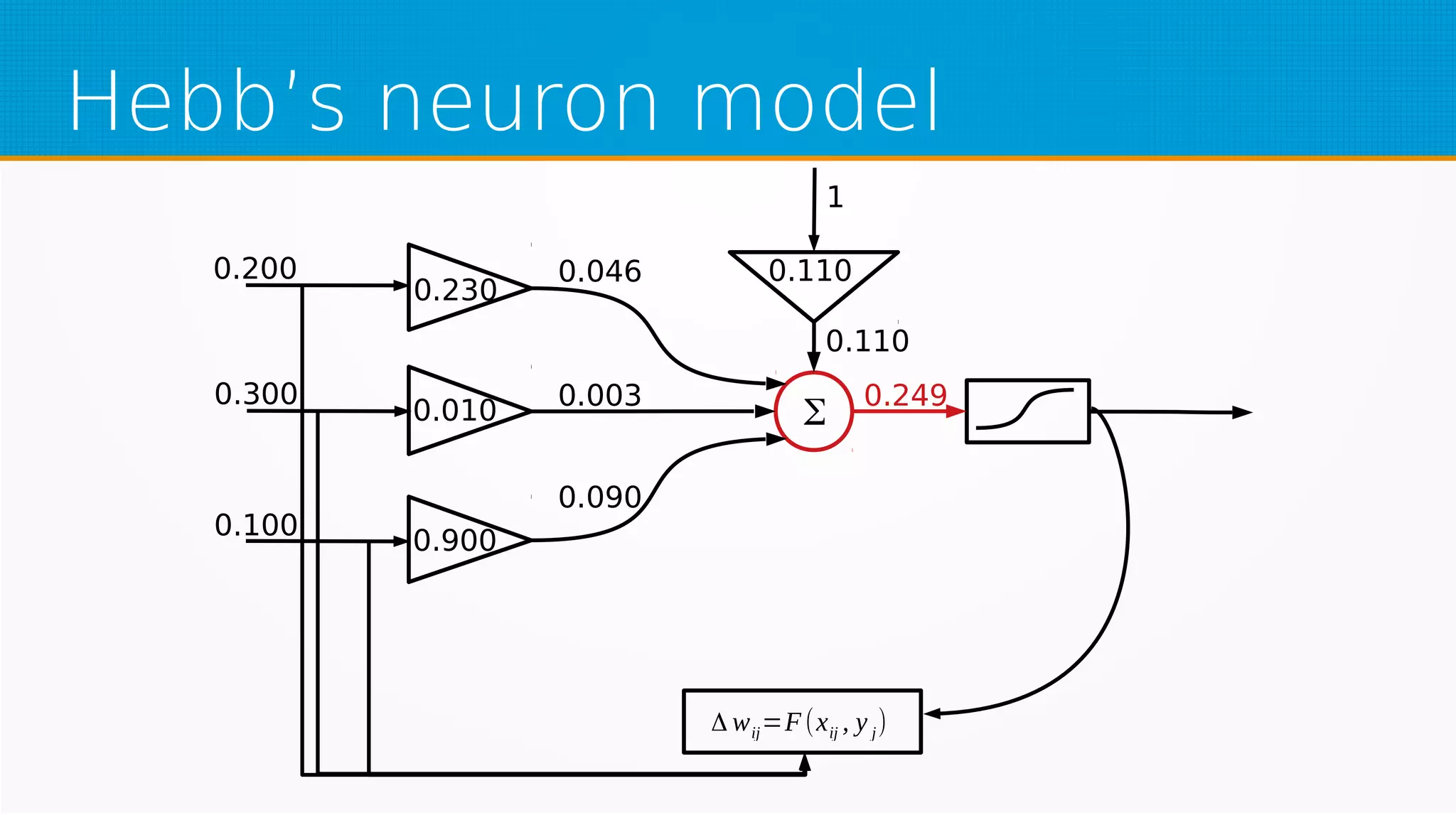
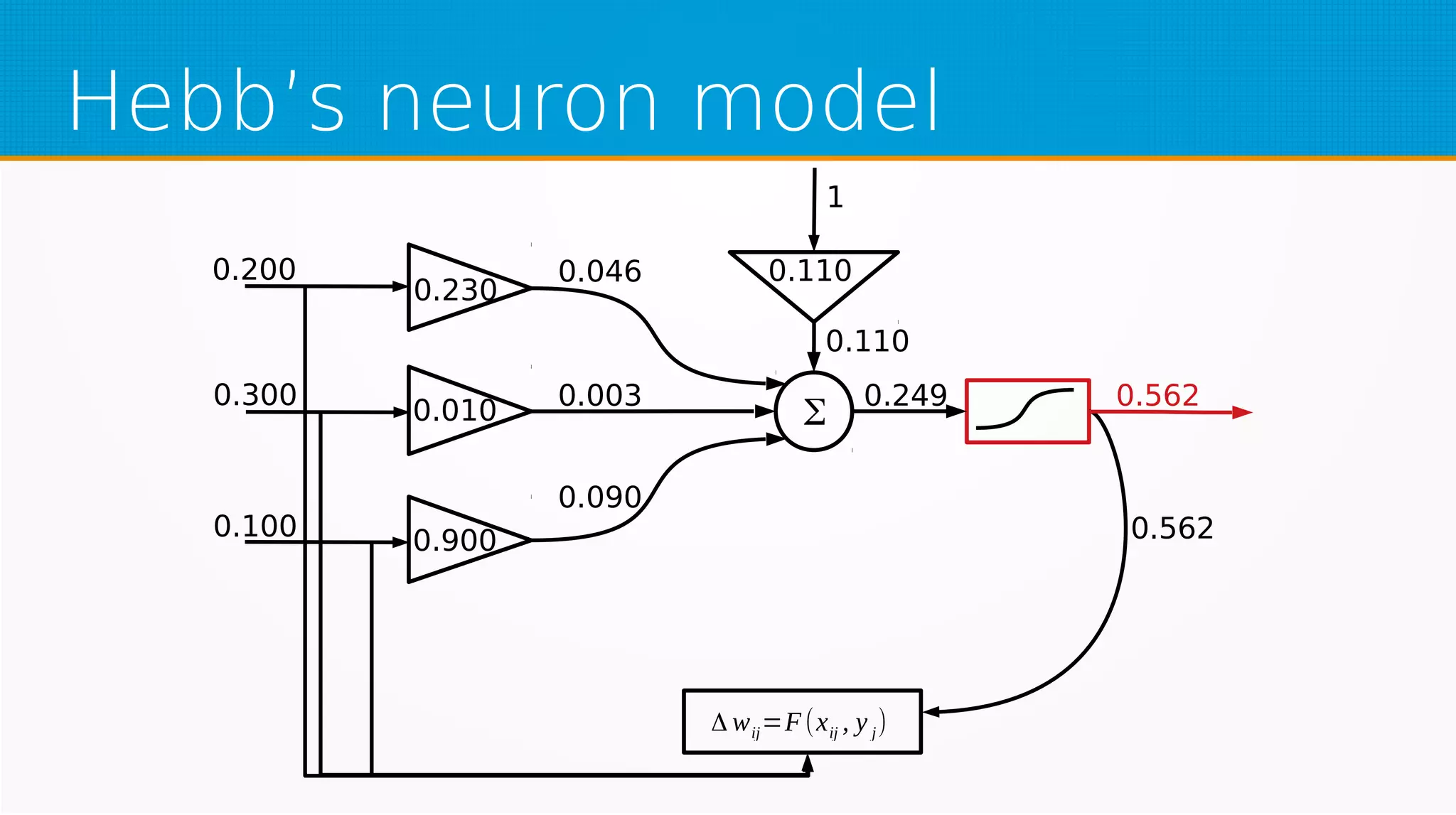
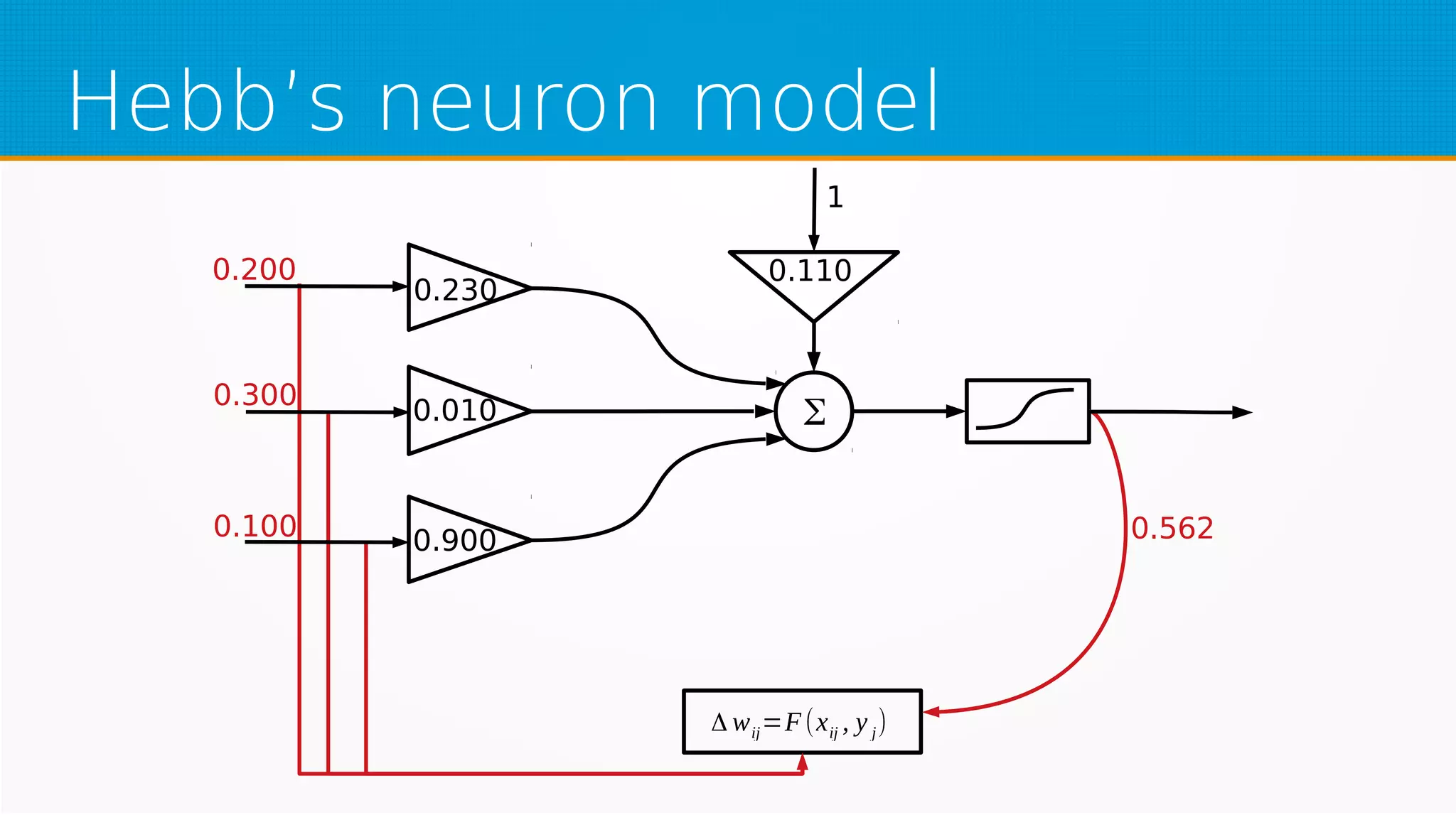
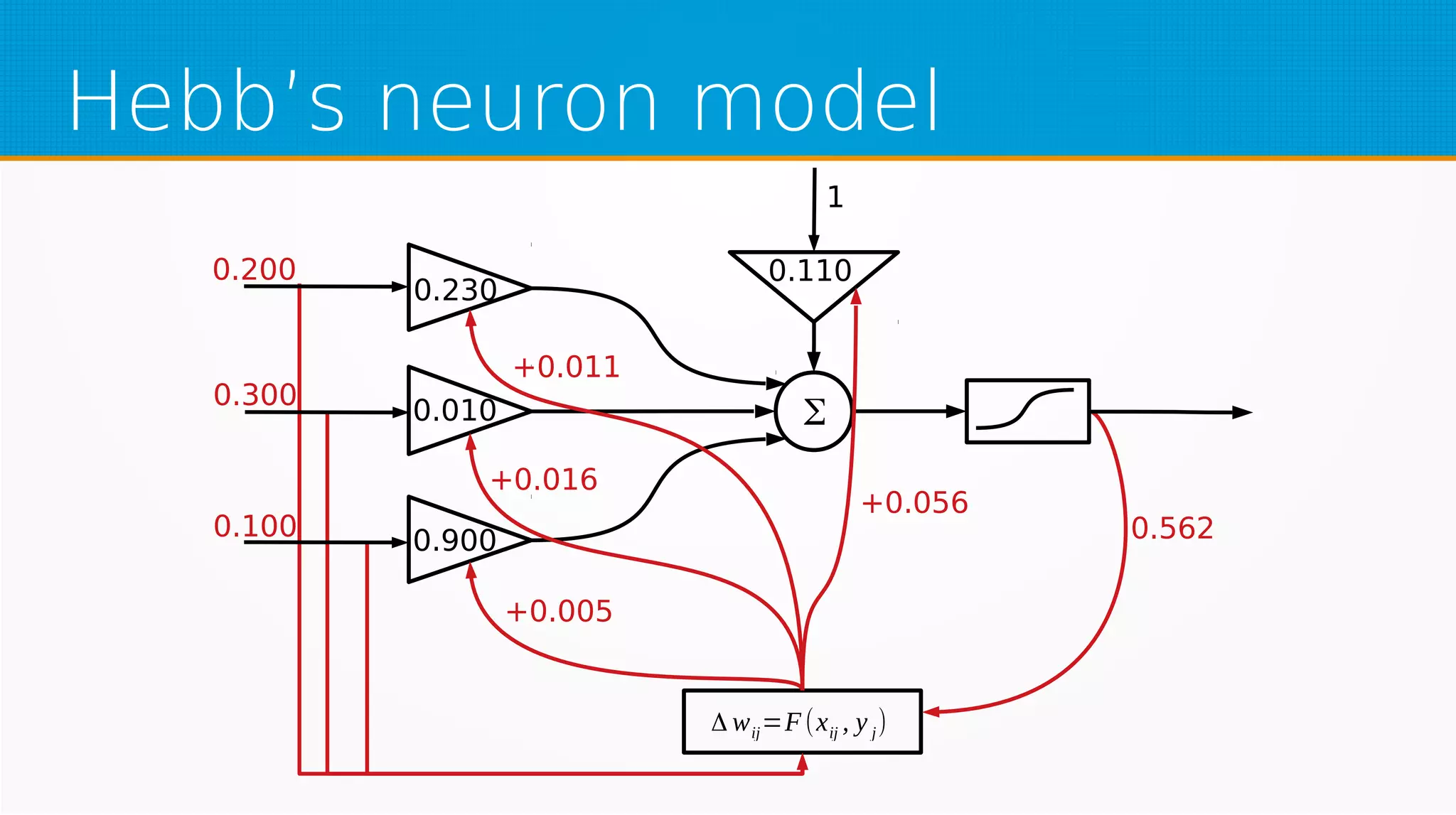
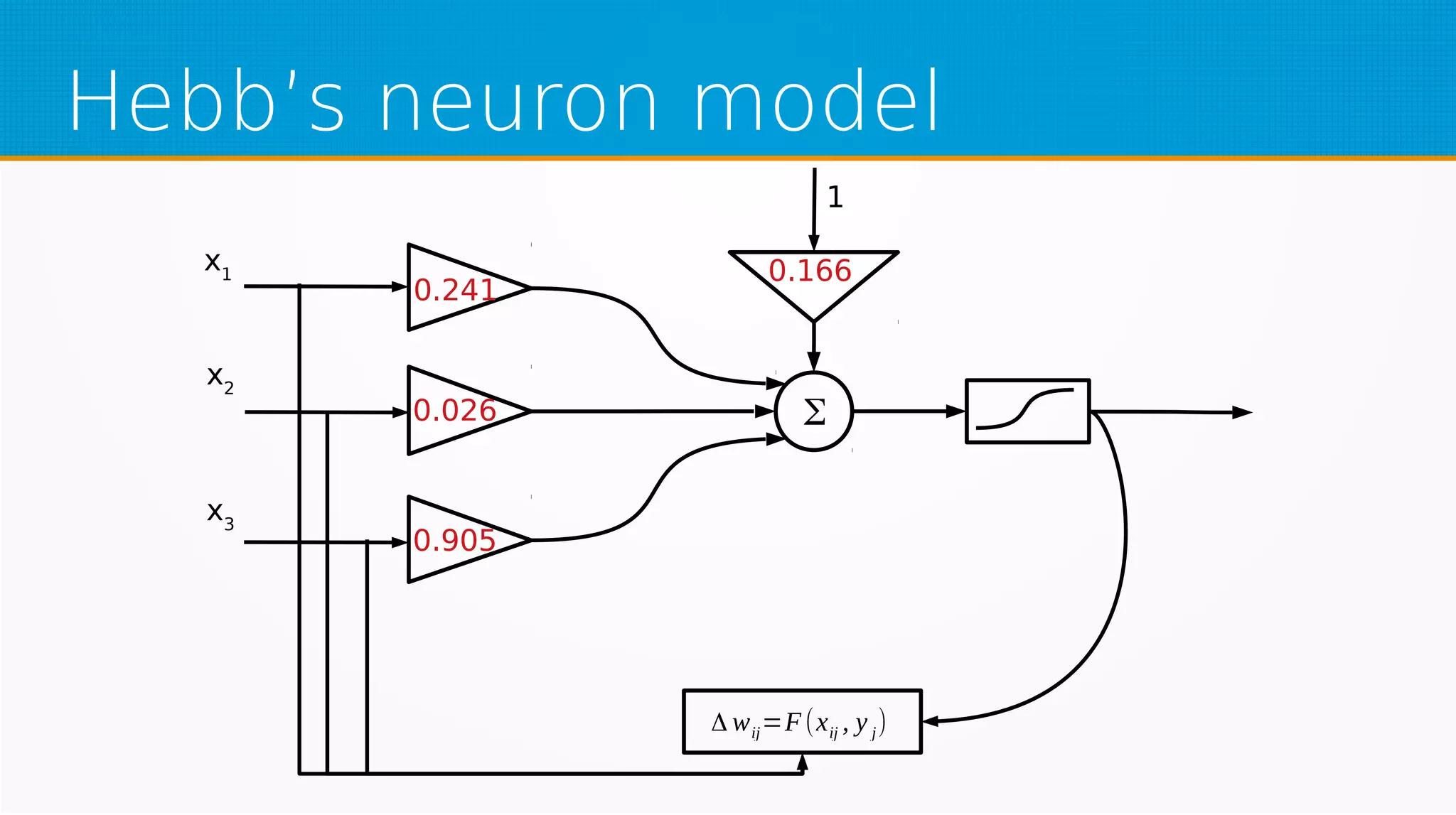
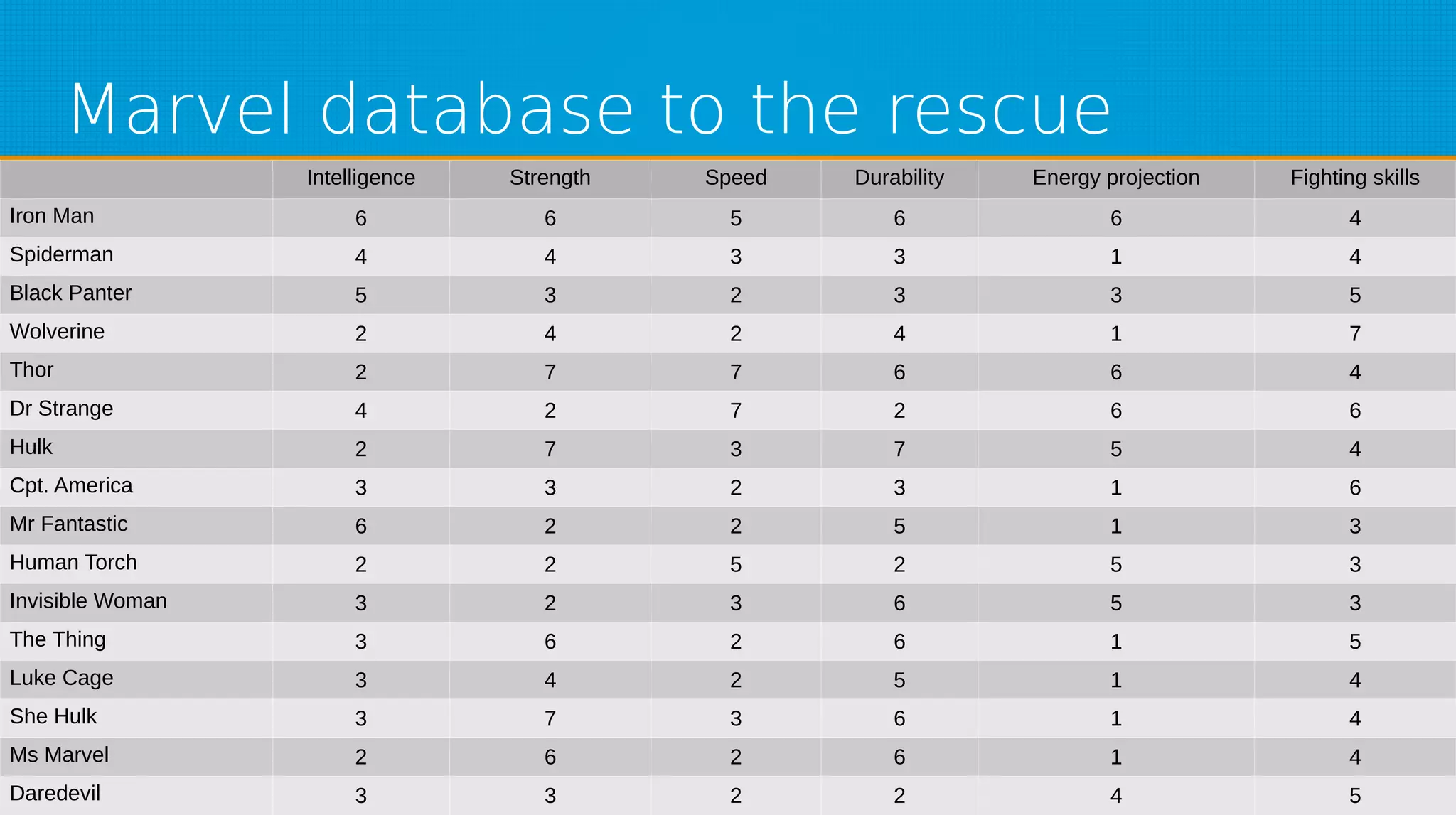
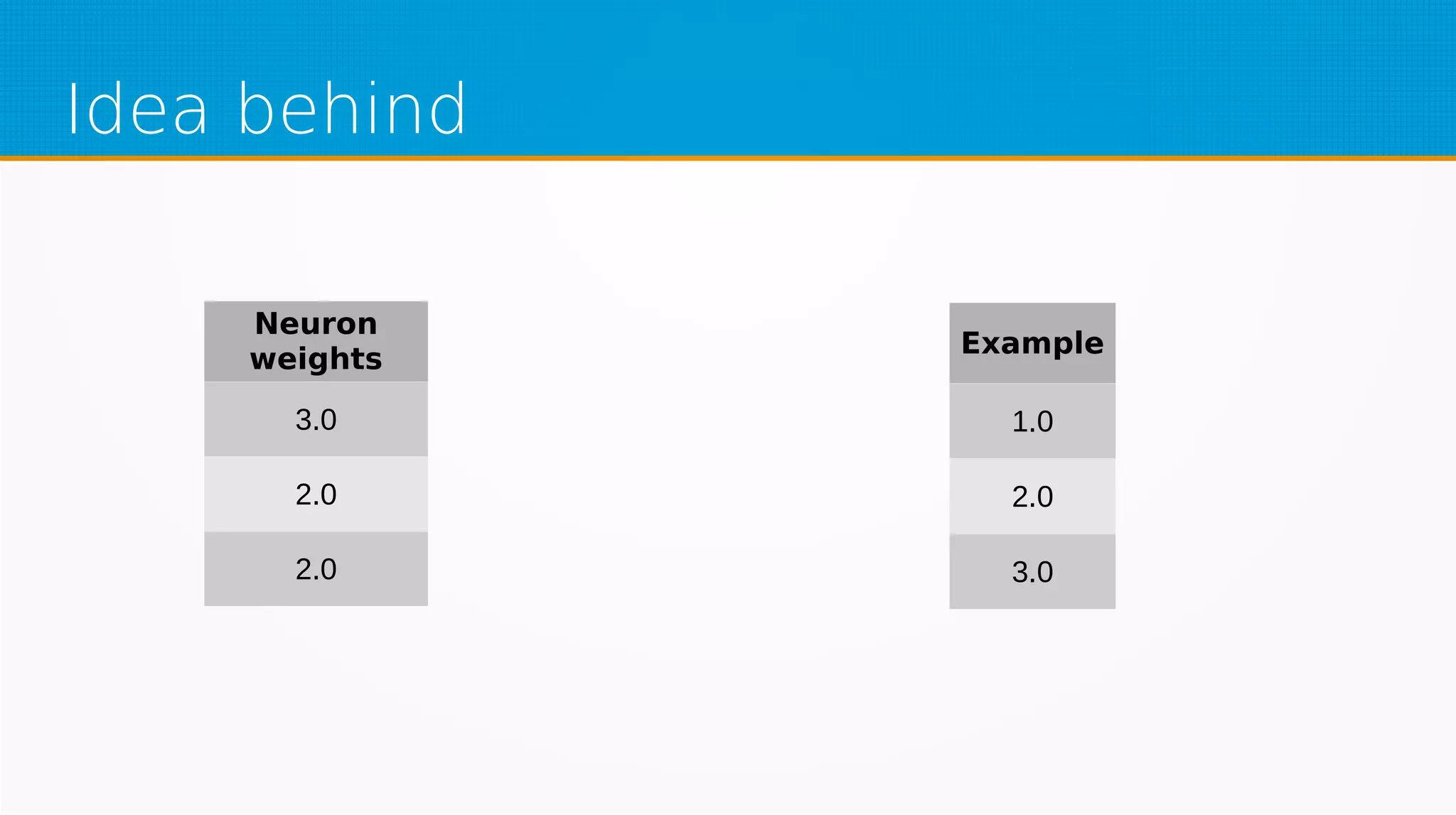
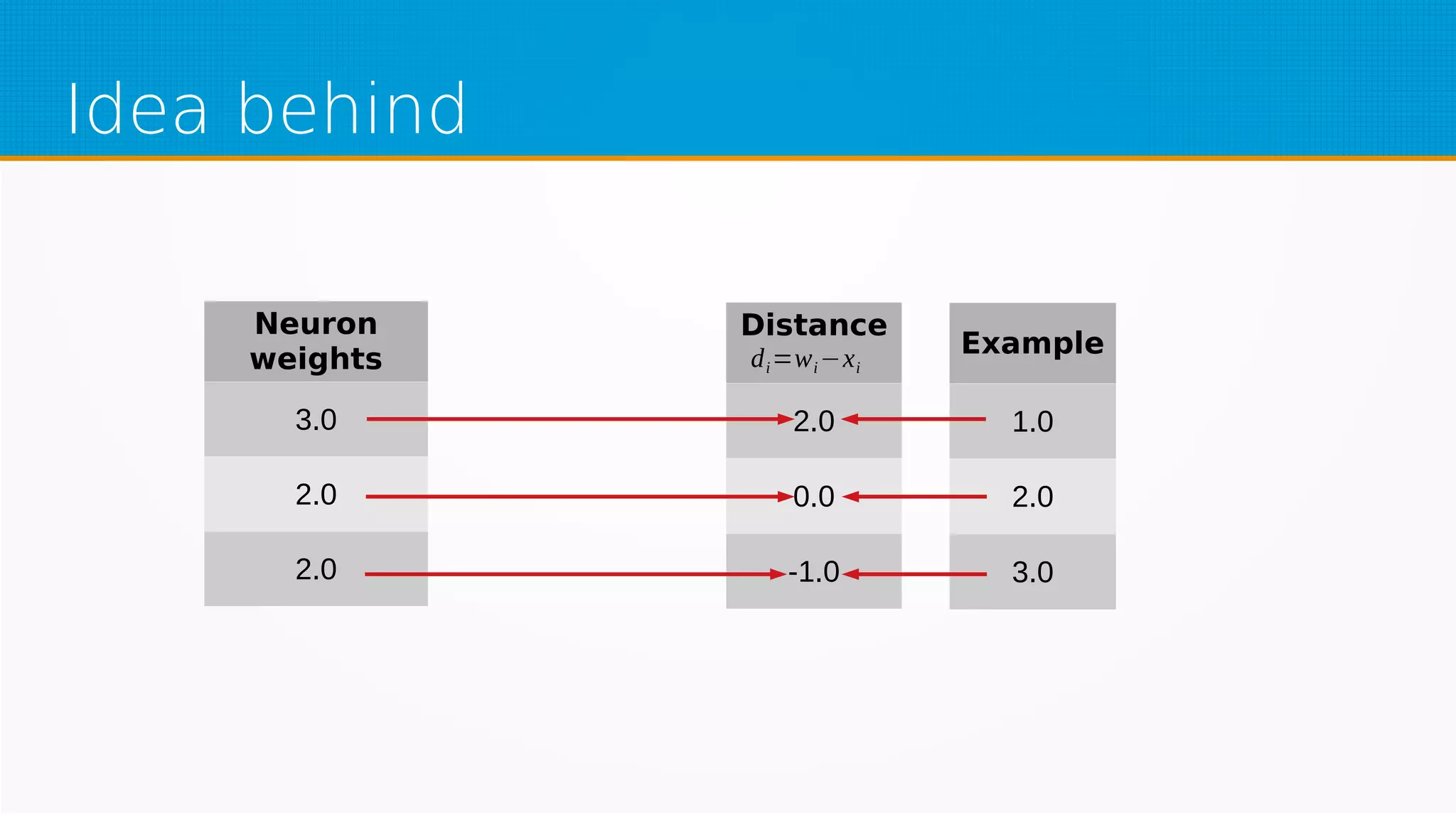
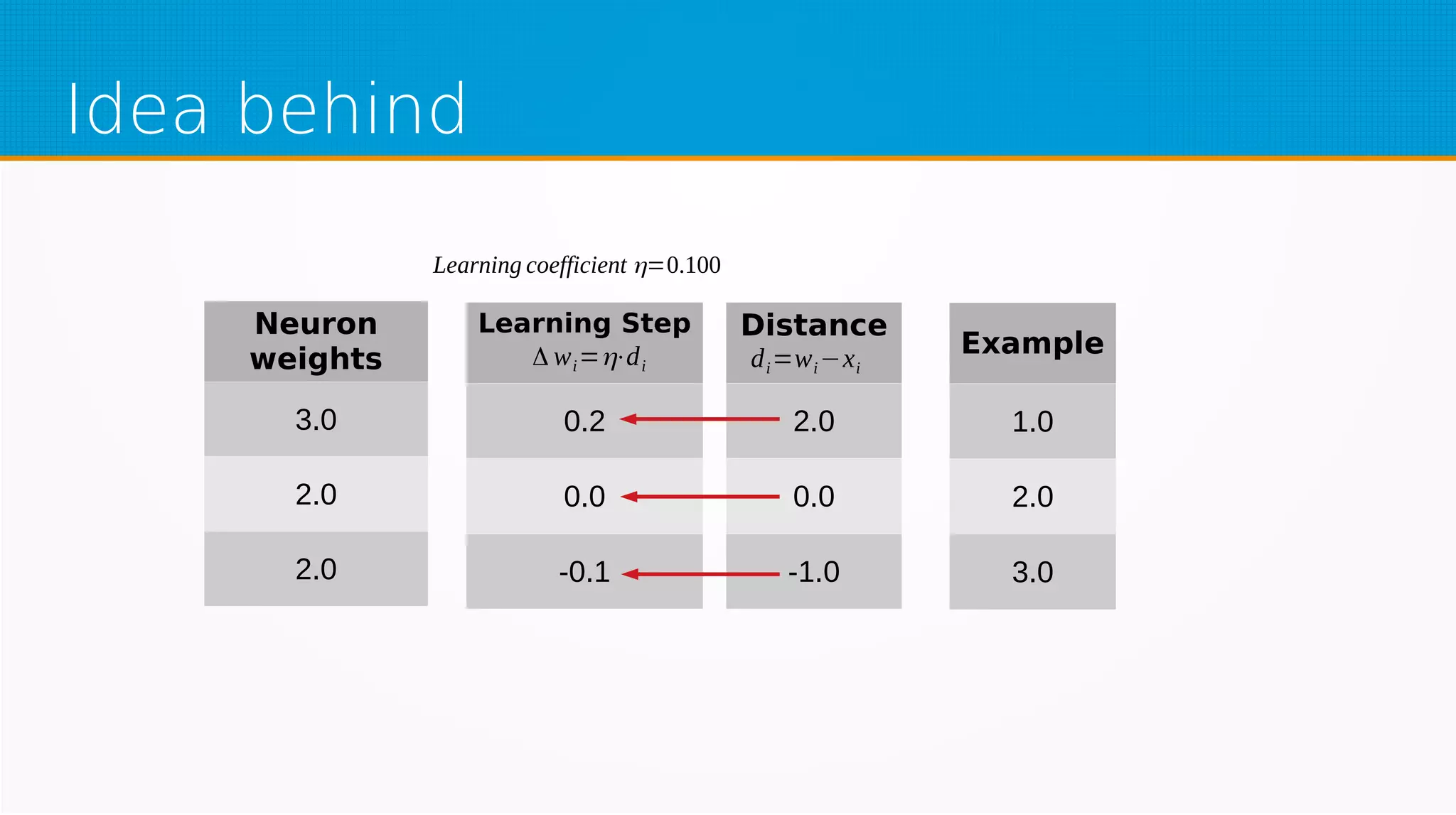
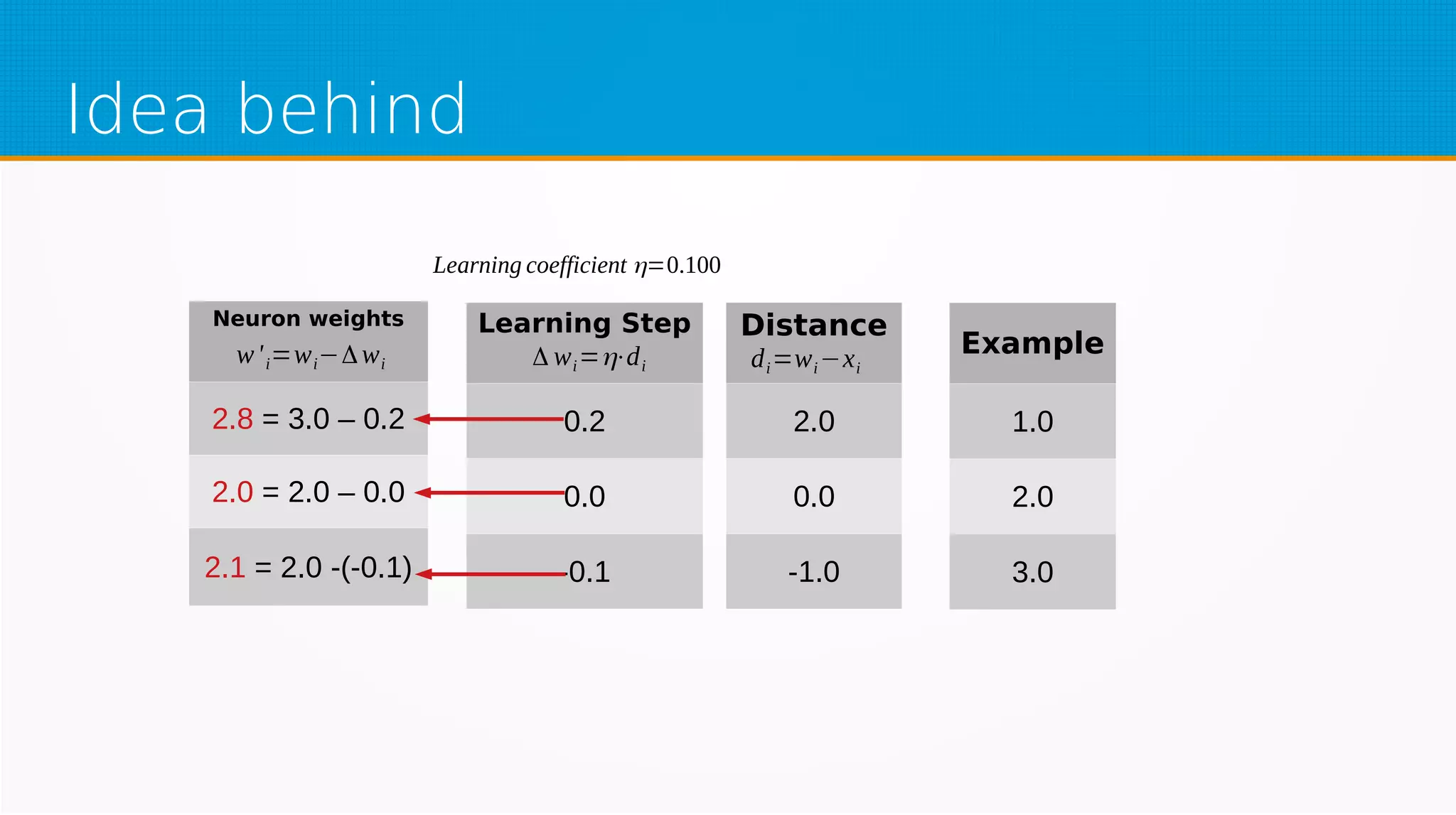
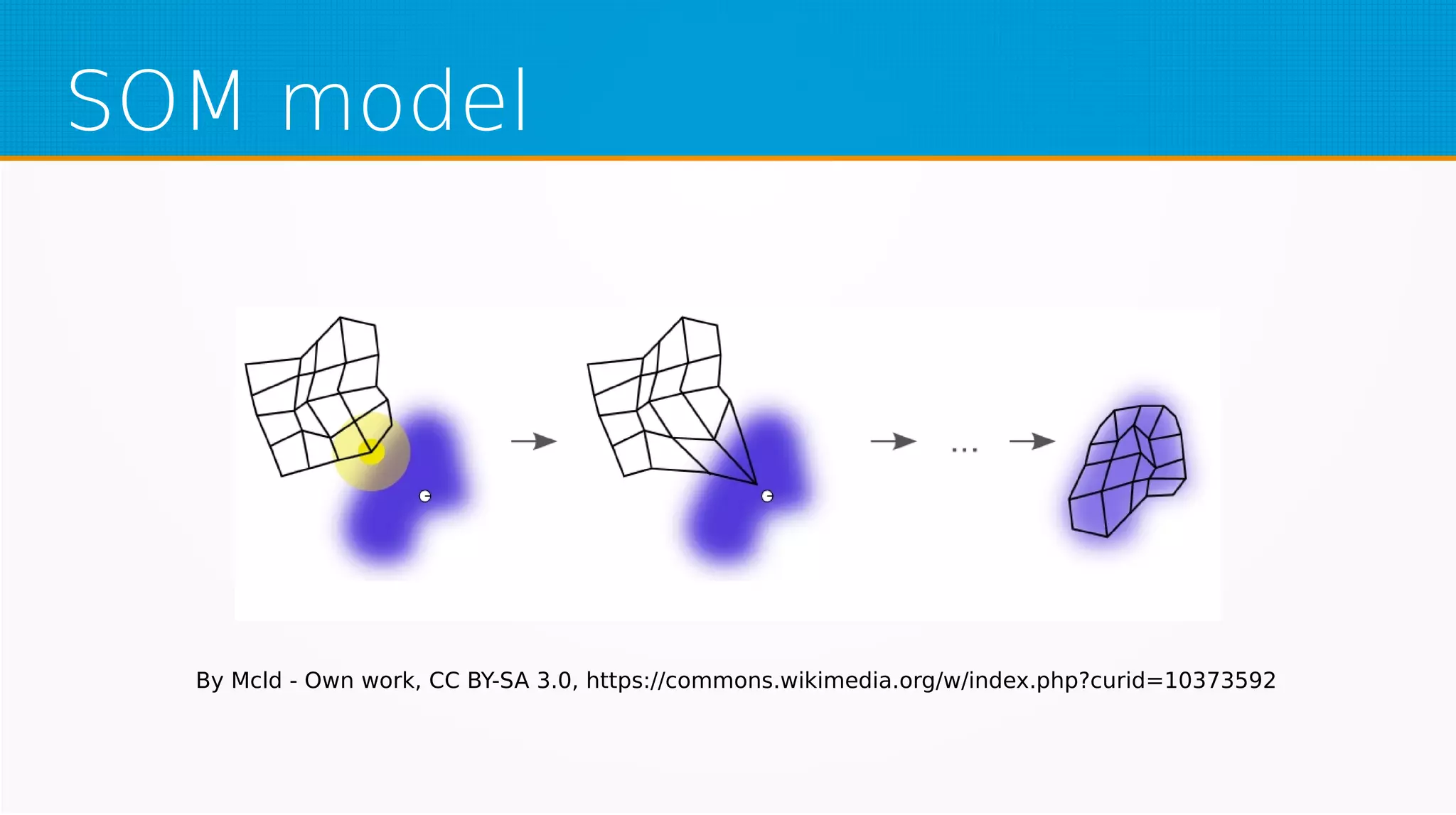
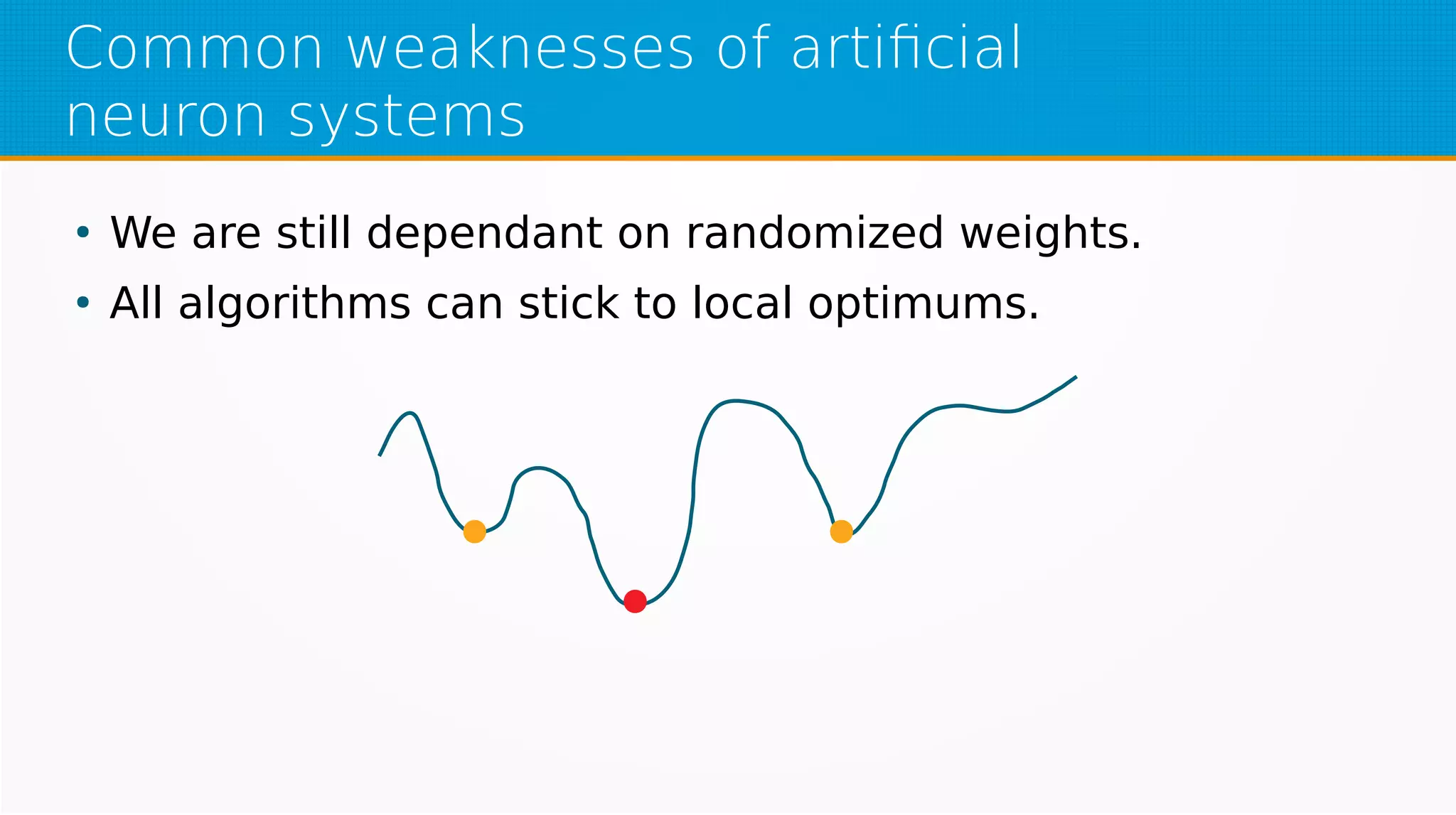
The document provides an overview of machine learning, covering key topics such as supervised and unsupervised learning, neural networks, linear regression, and gradient descent. It emphasizes the mathematical foundations of these concepts and illustrates practical applications including example scenarios like predicting comic book issues based on costume prices. Additionally, it discusses learning algorithms like Hebbian learning and self-organizing maps, highlighting their strengths and weaknesses.

1. achine Learning:
The Bare Math Behind Libraries
Piotr Czajka
Łukasz Gebel

3. Agenda
●
What is Machine Learning?
●
Supervised learning
●
Unsupervised learning
●
Q&A

4. Machine Learning
„Field of study that gives computers the ability to
learn without being explicitly programmed.”
Arthur Samuel

5. Machine Learning
„I consider every method that needs training
as intelligent or machine learning method.”
Our Lecturer

6. Supervised learning
●
It is similar to be tought by a teacher.

7. Supervised learning
●
Build your model that performs particular task:
– Prepare data set consisting of examples & expected
outputs

8. Supervised learning
●
Build your model that performs particular task:
– Prepare data set consisting of examples & expected
outputs
– Present examples to your model

9. Supervised learning
●
Build your model that performs particular task:
– Prepare data set consisting of examples & expected
outputs
– Present examples to your model
– Check how it responds (model’s output values)

10. Supervised learning
●
Build your model that performs particular task:
– Prepare data set consisting of examples & expected
outputs
– Present examples to your model
– Check how it responds (model’s output values)
– Adjust model’s params by comparing output values
with expected output values

11. Neural Networks
●
Inspired by biological brain mechanisms
●
Many applications:
– Computer vision
– Speech recognition
– Compression

12. Biological Neuron
http://www.marekrei.com/blog/wp-content/uploads/2014/01/neuron.png

13. Artificial Neuron
● Inputs (x1, … , xn) are features of single example
●
Multiply each input by weight, sum it and put the
sum as an argument of activation function
w1
w2
wn
w0
Σ
x1
x2
xn
...
s y

14. Activation function
●
Sigmoid
– Maps sum of neurons signals to value from 0 to 1
– Continous, nonlinear
– If input is positive it gives values > 0.5
f (x)=
1
1+e(−βx)

15. Linear Regression
●
Method for modelling relationship between
variables
●
Simplest form: how x relates to y
●
Examples:
– House size vs house price
– Voltage vs electric current

16. Real life problem

17. What defines a superhero?

18. Costume

19. Costume price vs number of issues
●
For given amount of money predict in how many
comic book issues you’ll appear.
Costume
price(x)
Number of issues
(y)
240 6370
480 8697
... ...
26 2200

20. Interesting fact
●
Invisible woman costume costs $120
Invisible woman

21. Linear regression
●
Let's have a function:
f (x ,Θ)=Θ1 x+Θ0
f (x,Θ)−number of comicbookissues
x−costume price
Θ−parameters

22. Let's plot

23. Let's plot

24. Let's plot

25. Warning!

26. Objective function
Q(Θ)=
1
2 N
∑
j=0
N
(f ( x
j
,Θ)−y
j
)
2
Q(Θ)−objectivefunction
N−numberof datasamples
j−indexof particulardatasample

27. Objective function - intuition
f (xj
,Θ)=4 y=2
(4−2)2
=22
=4
sum+=4

28. Objective function - intuition
f (xj
,Θ)=1 y=1
(1−1)2
=02
=0
sum+=0

29. Gradient descent
●
Find the minimum of the objective function
●
Iteratively update function parameters:
Θ0(t +1)=Θ0(t)−α
1
N
∑
j=0
N
(f ( x
j
,Θ)− y
j
)
Θ1(t +1)=Θ1(t )−α
1
N
∑
j=0
N
(f (x
j
,Θ)− y
j
) x
t−number of iteration
α−learning step

30. Gradient descent

31. Gradient descent
−α ∗ +derivative < 0

32. Gradient descent
−α ∗ +derivative < 0

33. Gradient descent
−α ∗ +derivative < 0

34. Gradient descent
−α ∗ +derivative < 0

35. Gradient descent
−α ∗ −derivative > 0

36. Gradient descent
−α ∗ −derivative > 0

37. Gradient descent
−α ∗ −derivative > 0

38. Gradient descent
−α ∗ −derivative > 0

39. Demo

40. Linearly separable problem

41. Not linearly separable problem

42. NN – random weights init
+1
+1
x1
x2
y

43. NN – feed forward
+1
+1
x1
x2
y

44. NN – feed forward
+1
+1
x1
x2
y

45. NN – feed forward
+1
+1
x1
x2
y

46. NN – feed forward
+1
+1
x1
x2
y

47. NN – compute error
+1
+1
x1
x2
y
( y−expected output)2

48. NN – backpropagation step
●
Use gradient descent and computed error
●
Update every weight of every neuron from
hidden and output layer

49. NN – backpropagation step
+1
+1
x1
x2
y
( y−expected output)2

50. NN – backpropagation step
+1
+1
x1
x2
y

51. Neural Network
„Neural networks are nothing more than
randomized optimization.”
Another Lecturer

52. Real life problem
●
You said it can solve non linear problems, let's
generate superhero logo using it.

53. Unsupervised learning

54. What? They can learn by themselves?

55. What? They can learn by themselves?

56. Why would we let them?
●
Less complex mathematical apparatus than in
supervised learning.
●
It is similar to discovering world on your own.

57. Idea behind – groups

58. Idea behind – groups

59. Idea behind – groups

60. Why would we let them?
Used mostly for sorting and grouping when:
●
Sorting key can’t be easily figured out.
●
Data is very complex and finding the key is not
trivial.

61. Hebbian learning

62. Hebbian learning
●
Works similar to the nature
●
Great for beginners and biological simulations :)
●
Simple Hebbian learning algorithm
Δ wij=η⋅xij⋅yi
Δ wij−change of j weight of ineuron
η−learningcoefficient
xij− jinput of ineuron
yi−output of i neuron

63. Hebbian learning
●
Works similar to the nature
●
Great for beginners and biological simulations :)
●
Generalised Hebbian learning algorithm
Δ wij=F(xij , yj)
Δ wij−change of j weight of ineuron
η−learningcoefficient
xij− jinput of ineuron
yi−output of i neuron

64. Hebb’s neuron model
w1
w2
wn
w0
Δ wij=F(xij , y j)
Σ
x1
x2
xn
...
1
s y

65. Hebb’s neuron model
0.230
0.010
0.900
0.110
Δ wij=F(xij , y j)
Σ
0.200
0.300
0.100
1

66. Hebb’s neuron model
0.230
0.010
0.900
0.110
Δ wij=F(xij , y j)
Σ
1
0.046
0.003
0.090
0.110
0.200
0.300
0.100

67. Hebb’s neuron model
0.230
0.010
0.900
0.110
Δ wij=F(xij , y j)
Σ
1
0.046
0.003
0.090
0.110
0.249
0.200
0.300
0.100

68. Hebb’s neuron model
0.230
0.010
0.900
0.110
Δ wij=F(xij , y j)
Σ
1
0.046
0.003
0.090
0.110
0.249 0.562
0.562
0.200
0.300
0.100

69. Hebb’s neuron model
0.230
0.010
0.900
0.110
Δ wij=F(xij , y j)
Σ
1
0.562
0.200
0.300
0.100

70. Hebb’s neuron model
0.230
0.010
0.900
0.110
Δ wij=F(xij , y j)
Σ
1
0.562
+0.011
+0.016
+0.005
+0.056
0.300
0.100
0.200

71. Hebb’s neuron model
0.241
0.026
0.905
0.166
Δ wij=F(xij , y j)
Σ
x1
x2
x3
1

72. Demo

73. Imagine superhero teams

74. Marvel database to the rescue
Intelligence Strength Speed Durability Energy projection Fighting skills
Iron Man 6 6 5 6 6 4
Spiderman 4 4 3 3 1 4
Black Panter 5 3 2 3 3 5
Wolverine 2 4 2 4 1 7
Thor 2 7 7 6 6 4
Dr Strange 4 2 7 2 6 6
Hulk 2 7 3 7 5 4
Cpt. America 3 3 2 3 1 6
Mr Fantastic 6 2 2 5 1 3
Human Torch 2 2 5 2 5 3
Invisible Woman 3 2 3 6 5 3
The Thing 3 6 2 6 1 5
Luke Cage 3 4 2 5 1 4
She Hulk 3 7 3 6 1 4
Ms Marvel 2 6 2 6 1 4
Daredevil 3 3 2 2 4 5

75. Hebbian learning weaknesses
●
Unstable.
●
Prone to rise the weights ad infinitum.
●
Some groups can trigger no response.
●
Some groups may trigger response from too
many neurons.

76. And now – self organising networks

77. Self organising?

78. Learning with concurrency
●
You try to generalize input vector in weights vector.
●
Instead of checking the reaction to input - you
check distance between both vectors.
●
Ideally – each neuron specializes in one class
generalization.
●
Two main strategies:
– Winner Takes All (WTA)
– Winner Takes Most (WTM)

79. Idea behind
Neuron
weights
3.0
2.0
2.0
Example
1.0
2.0
3.0

80. Example
1.0
2.0
3.0
Idea behind
Distance
2.0
0.0
-1.0
Neuron
weights
3.0
2.0
2.0
di=wi−xi

81. Distance
2.0
0.0
-1.0
Idea behind
Neuron
weights
3.0
2.0
2.0
Learning coefficient η=0.100
Learning Step
0.2
0.0
-0.1
Δ wi=η⋅di
Example
1.0
2.0
3.0
di=wi−xi

82. Idea behind
Distan
ce
2.0
0.0
-1.0
Neuron weights
2.8 = 3.0 – 0.2
2.0 = 2.0 – 0.0
2.1 = 2.0 -(-0.1)
Exam
ple
1.0
2.0
3.0
di=wi−xi
Learning coefficient η=0.100
Learning
Step
0.2
0.0
-0.1
w'i=wi−Δwi Δ wi=η⋅di
Example
1.0
2.0
3.0
Learning Step
0.2
0.0
-0.1
Δ wi=η⋅di
Distance
2.0
0.0
-1.0
di=wi−xi

83. Idea behind
Neuron
weights
2.8
2.0
2.1

84. Idea behind – initial setup
1
2 3

85. Idea behind – mid learning
1
2
3

86. Idea behind – homeostasis
1
2
3

87. Demo time

88. Learning with concurrency
●
Gives more diverse groups.
●
Less prone to clustering (than Hebb’s).
●
Searches wider spectrum of answers.
●
First step to more complex networks.

89. Learning with concurency -
weaknesses
●
WTA – works best if teaching examples are
evenly distributed in solution space.
●
WTM – works best if weights’ vectors are evenly
distributed in solution space.
●
Still can stick to local optimum.

90. Teuvo Kohonen’s SOM
Created by this nice guy here

91. Kohonen’s self-organizing map
●
The most popular self-organizing network with
concurrency algorithm.
●
It teaches groups of neurons with WTM alghoritm
●
Special features:
– Neurons are organised in a grid
– Nevertheless – they are treated as a single layer

92. Kohonen’s self-organizing map
wij(s+1)=wij(s)+Θ(kbest ,i , s)⋅η(s)⋅(I j(s)−wij(s))
s−epochnumber
kbest−best neuron
wij (s)− j weight of ineuron
Θ(kbest ,i,s)−neighbourhood function
η(s)−learning coefficient for sepoch
I j(s)− jchunk of example for s epoch

93. SOM model
By Mcld - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=10373592

94. Common weaknesses of artificial
neuron systems
●
We are still dependant on randomized weights.
●
All algorithms can stick to local optimums.

95. Thank you

96. Bibliography
●
https://www.coursera.org/learn/machine-learning
●
https://www.coursera.org/specializations/deep-learning
●
Math for Machine Learning - Amazon Training and Certification
●
Linear and Logistic Regression - Amazon Training and Certification
●
Grus J., Data Science from Scratch: First Principles with Python
●
Patterson J., Gibson A., Deep Learning: A Practitioner's Approach
●
https://github.com/massie/octave-nn- neural network Octave implementation
●
https://www.desmos.com/calculator/dnzfajfpym - Nanananana … Batman equation ;)
●
https://xkcd.com/605/ - extrapolating ;)
●
http://dilbert.com/strip/2013-02-02 - Dilbert & Machine Learning
●
Presentation + code: https://bitbucket.org/medwith/public/downloads/ml-math-jotb.zip