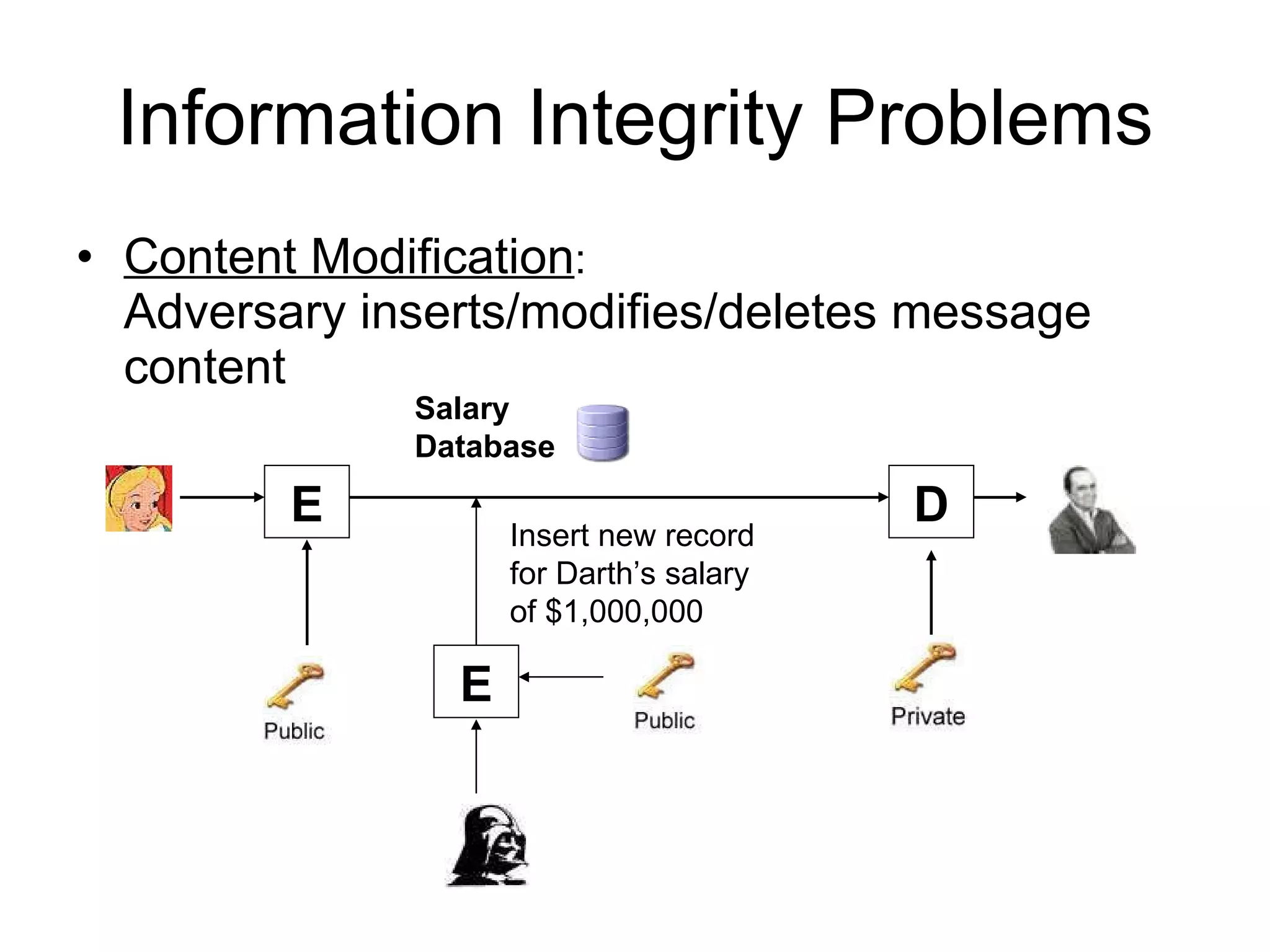
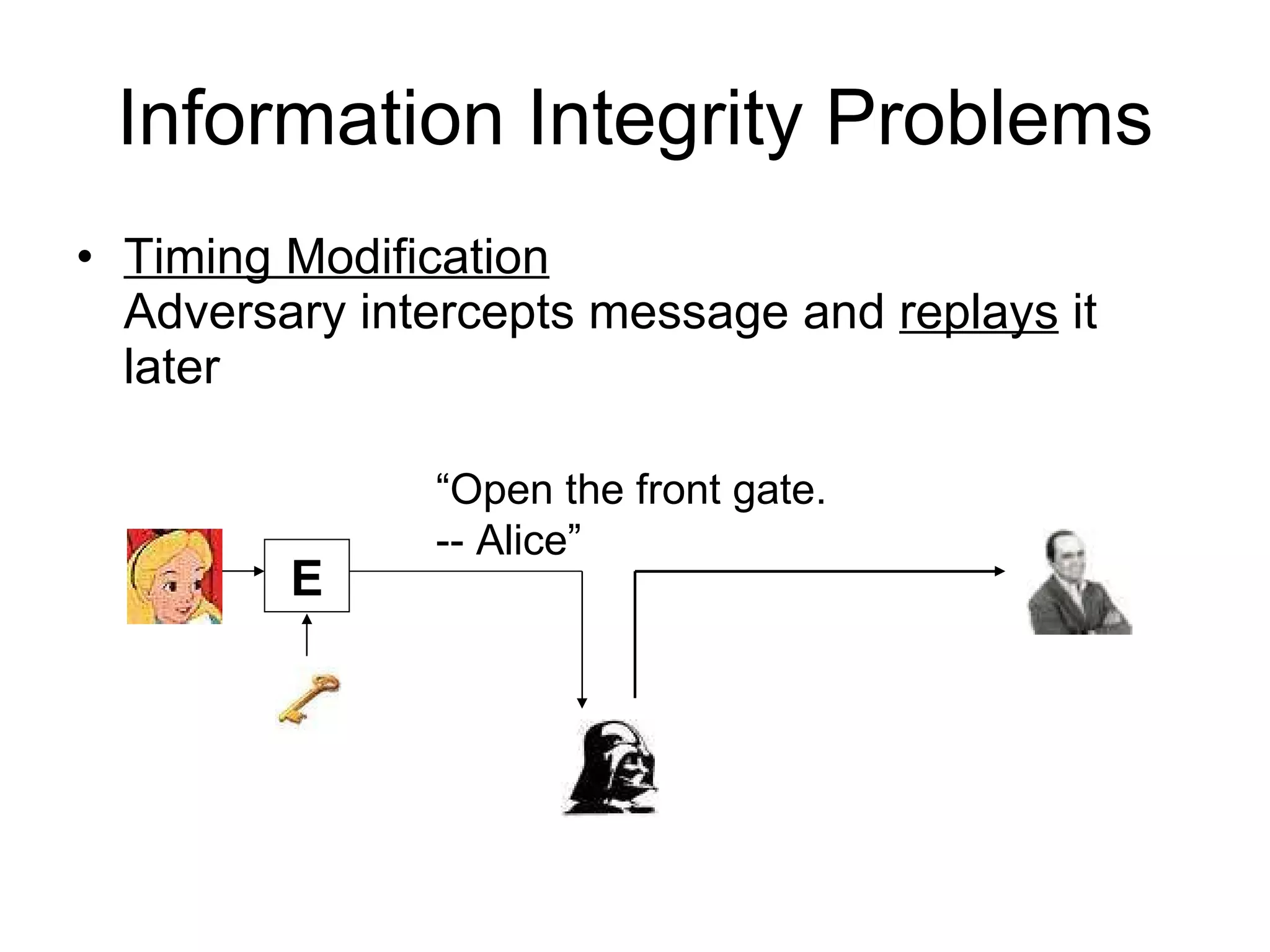
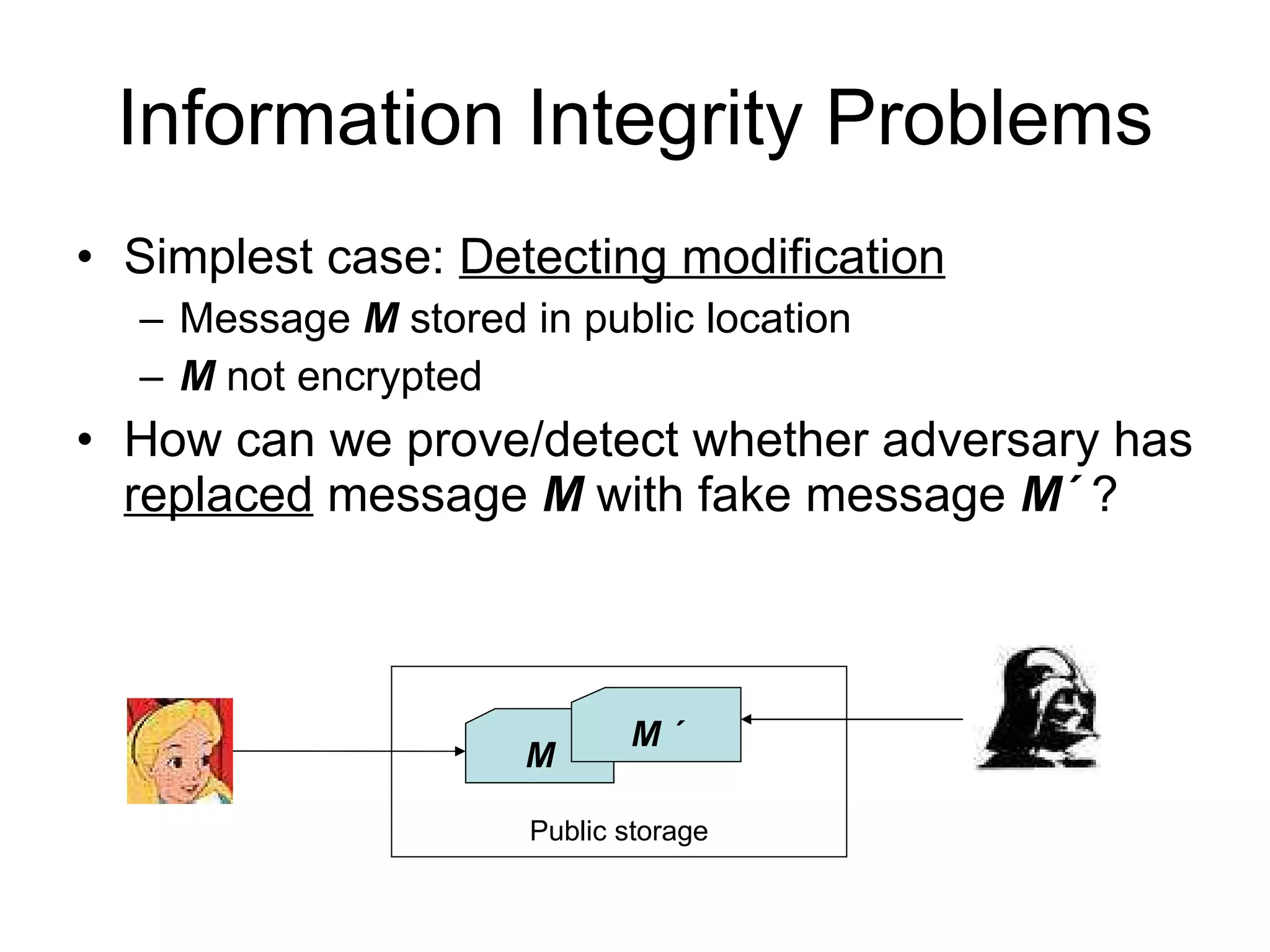
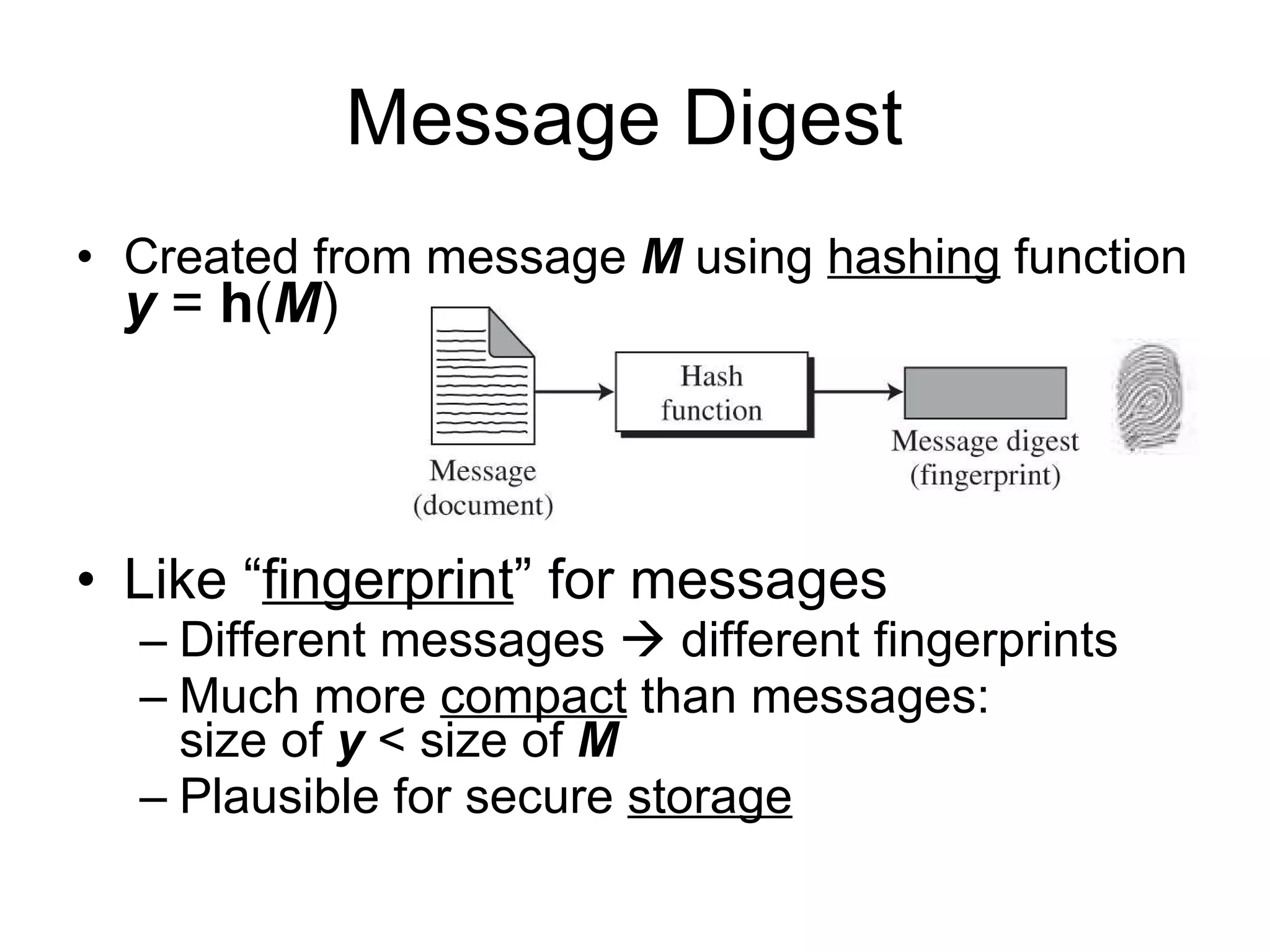
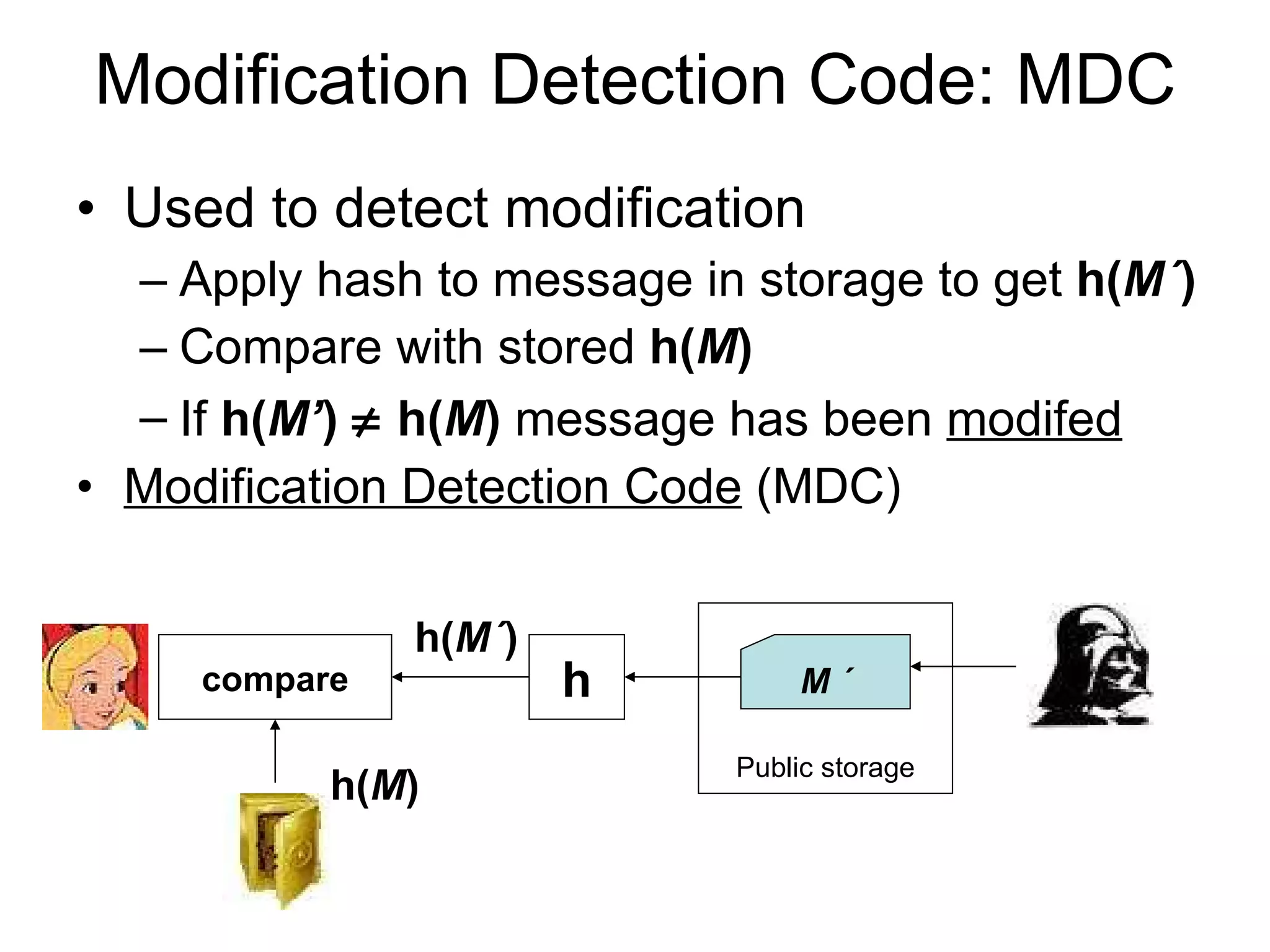
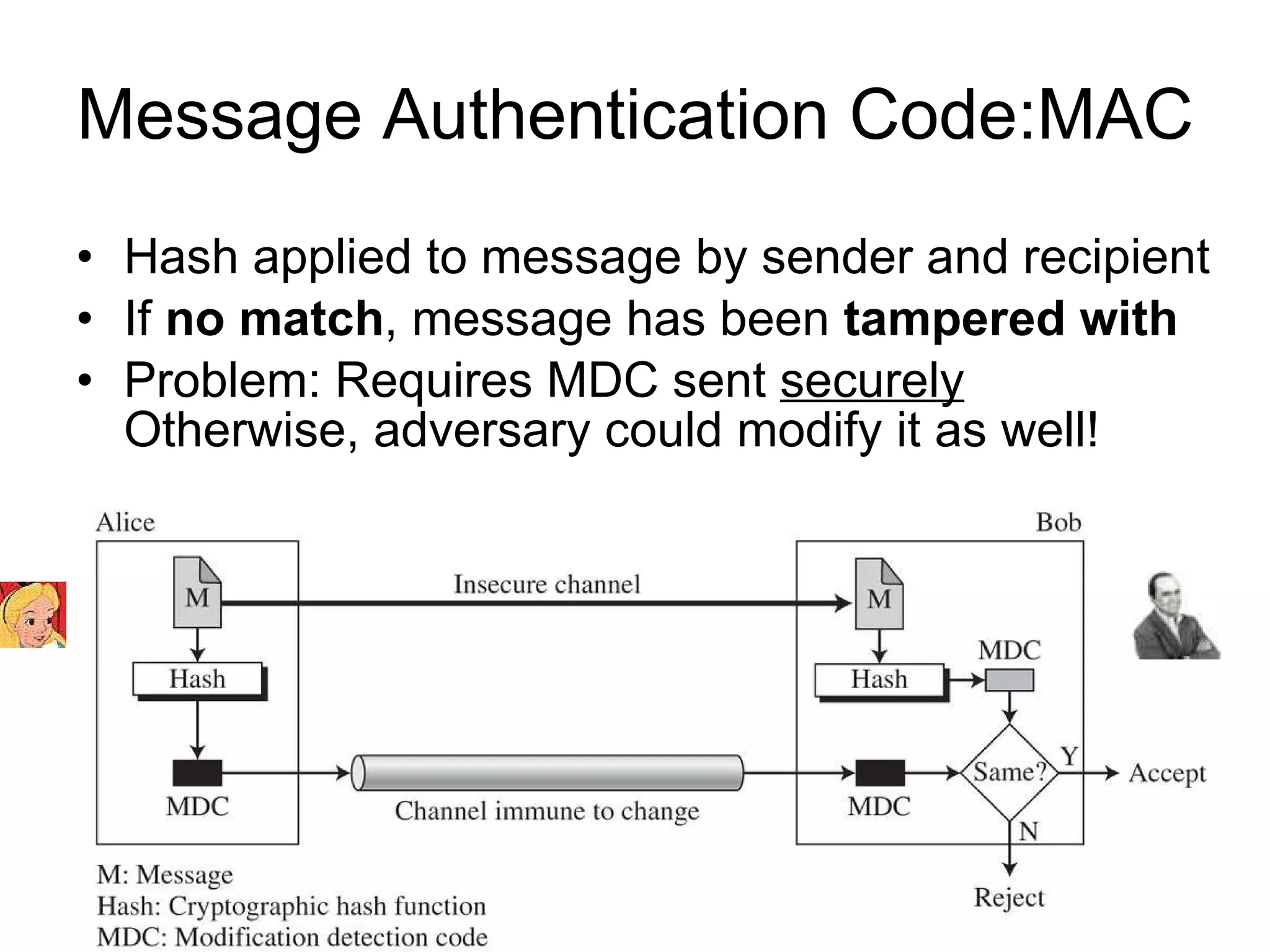
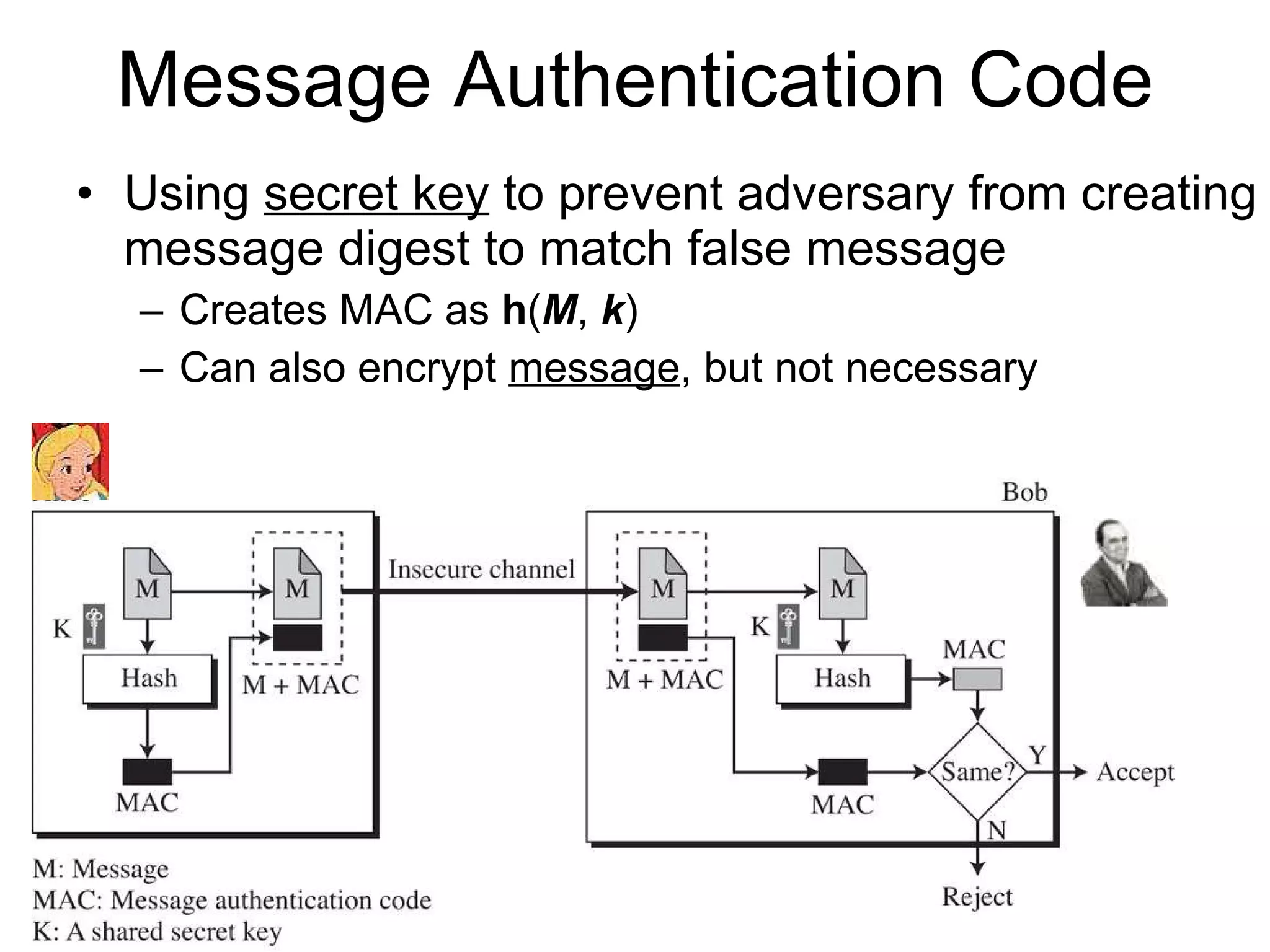
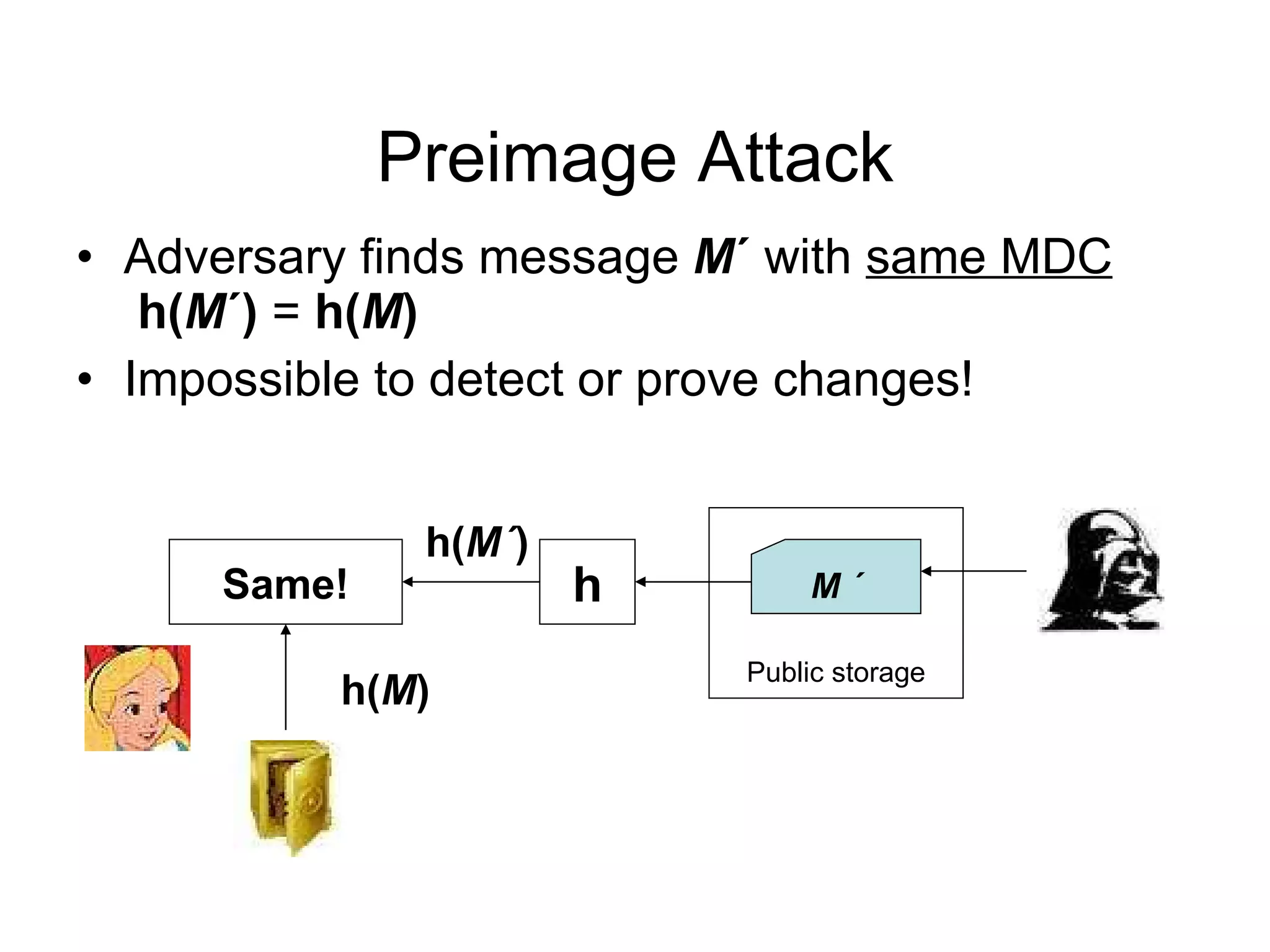
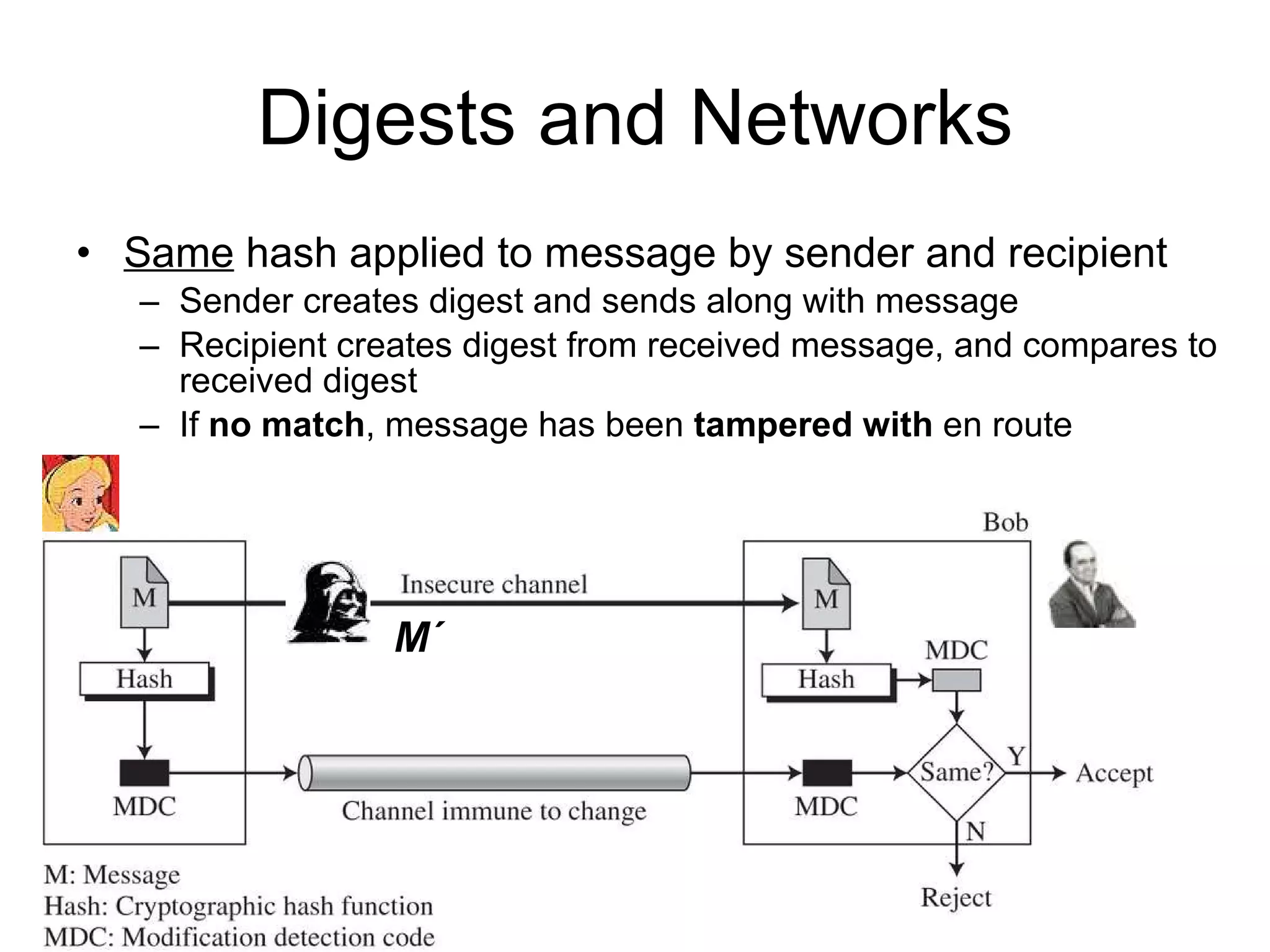
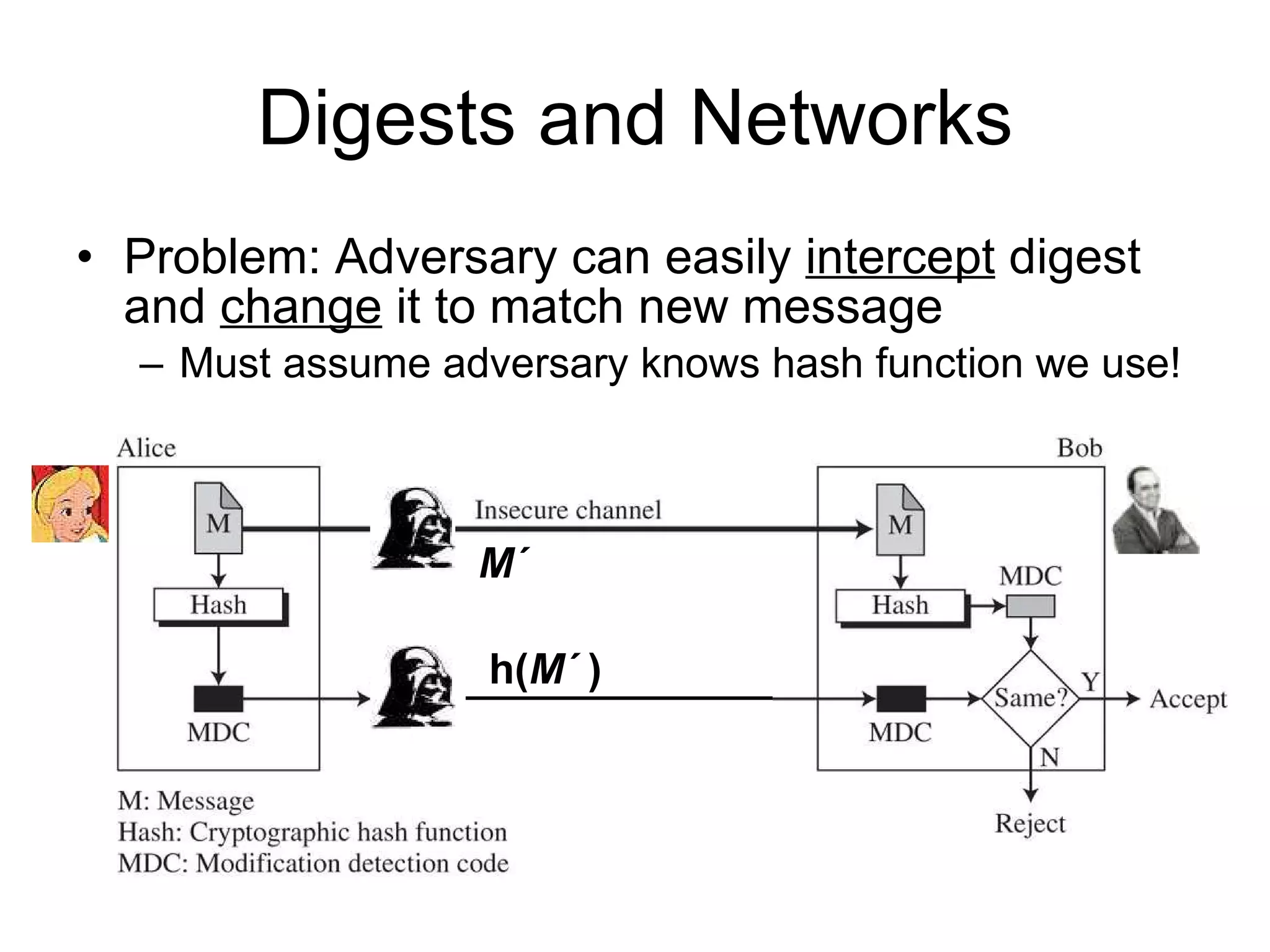
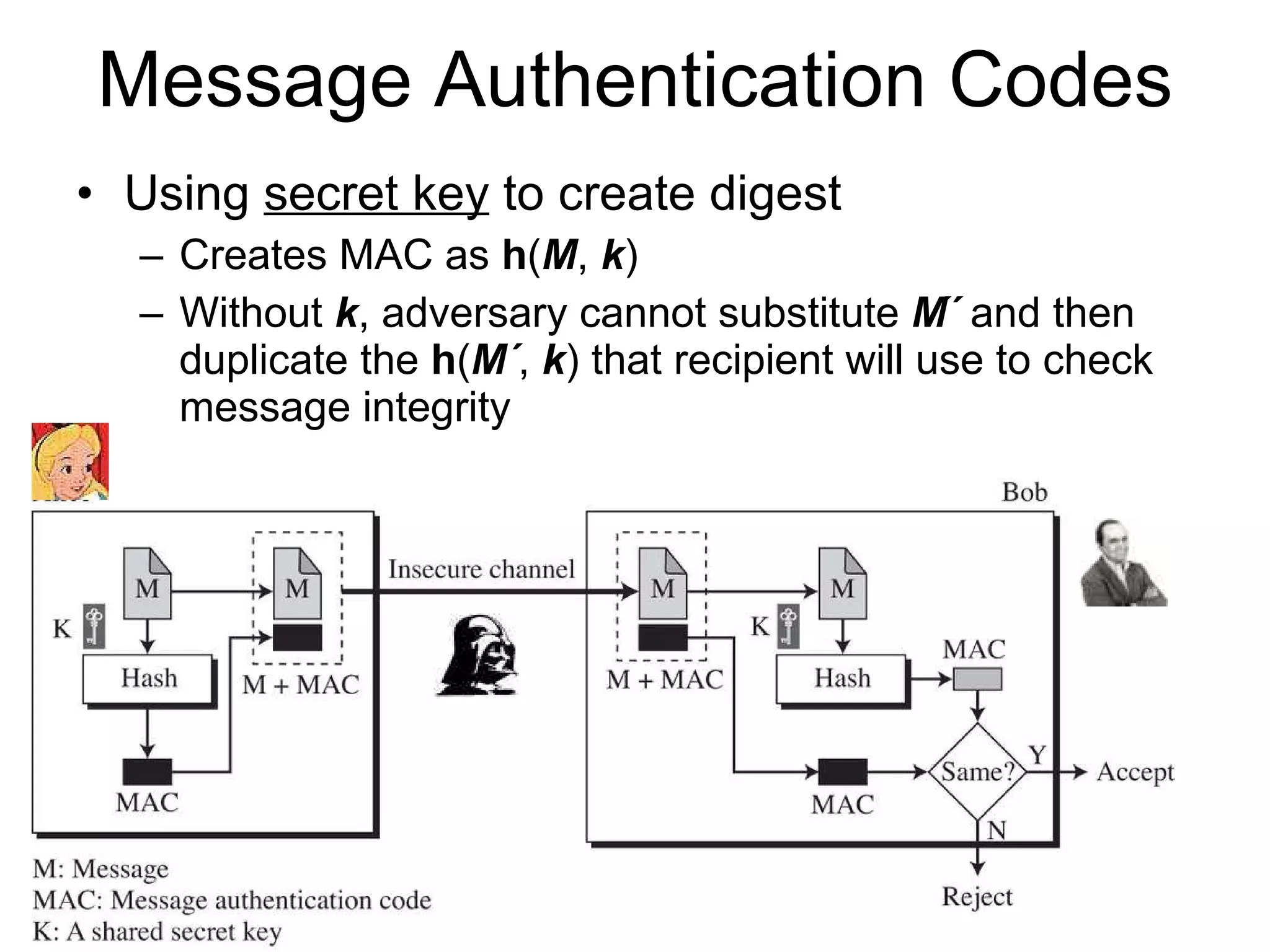
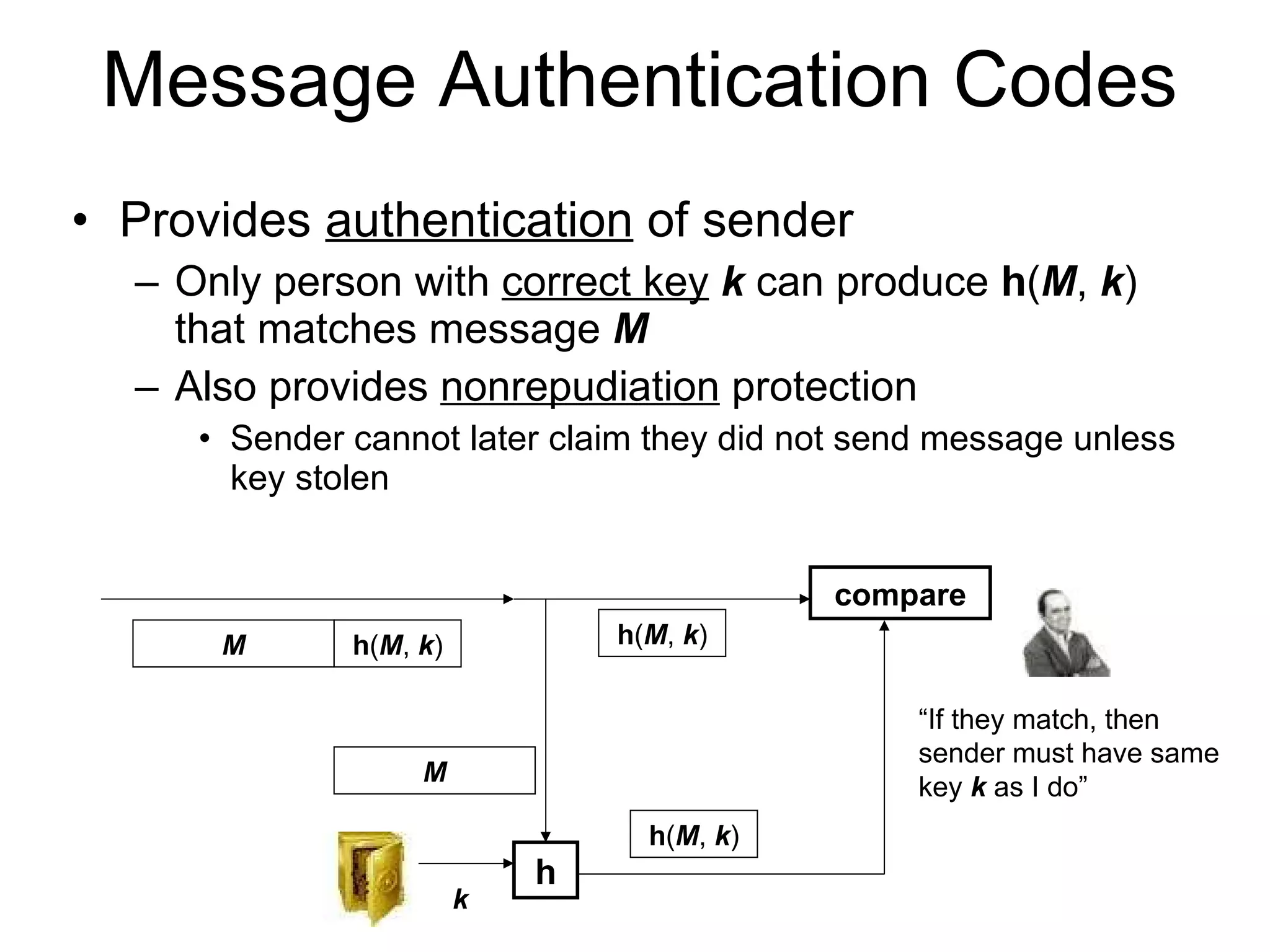
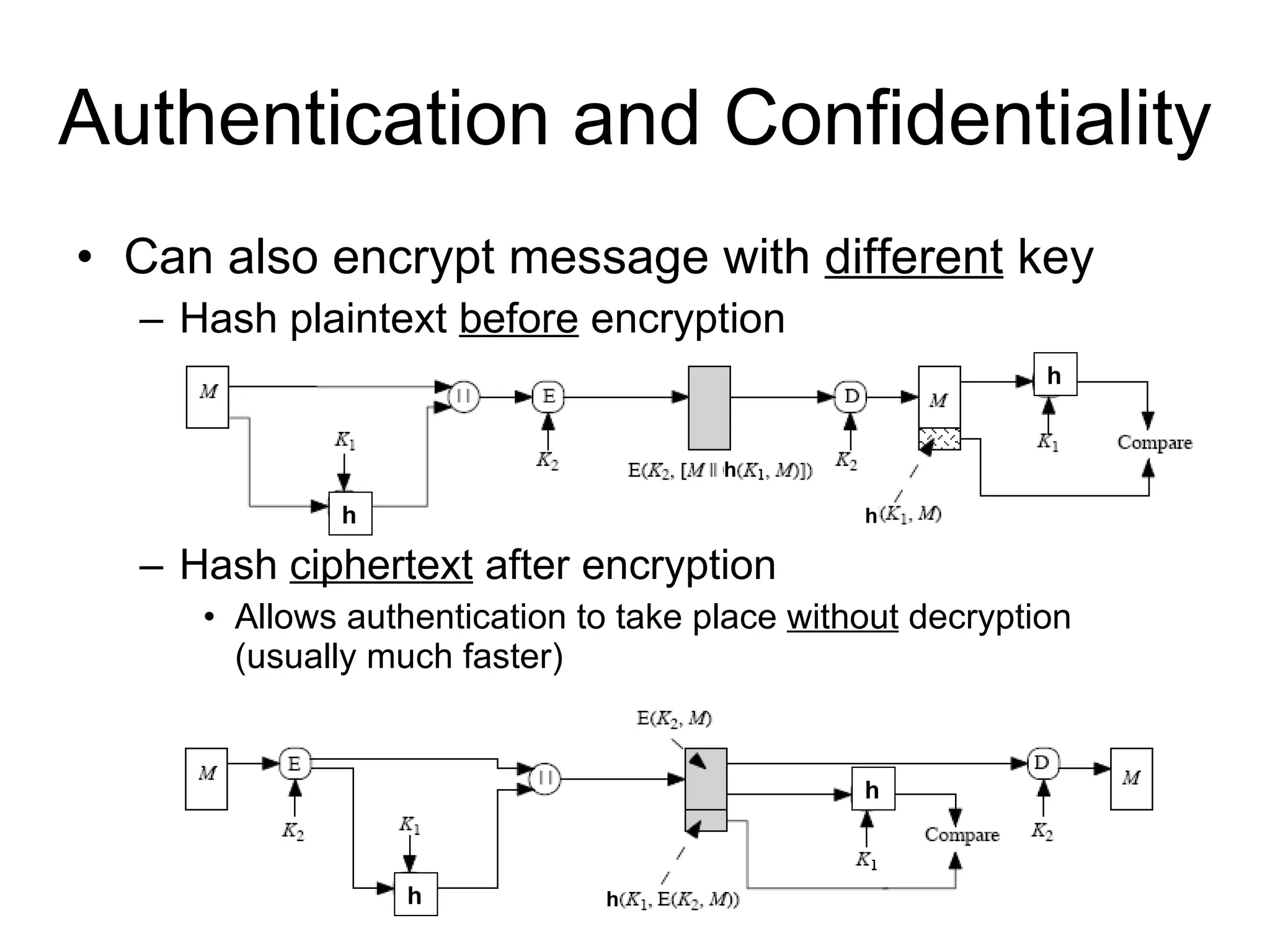
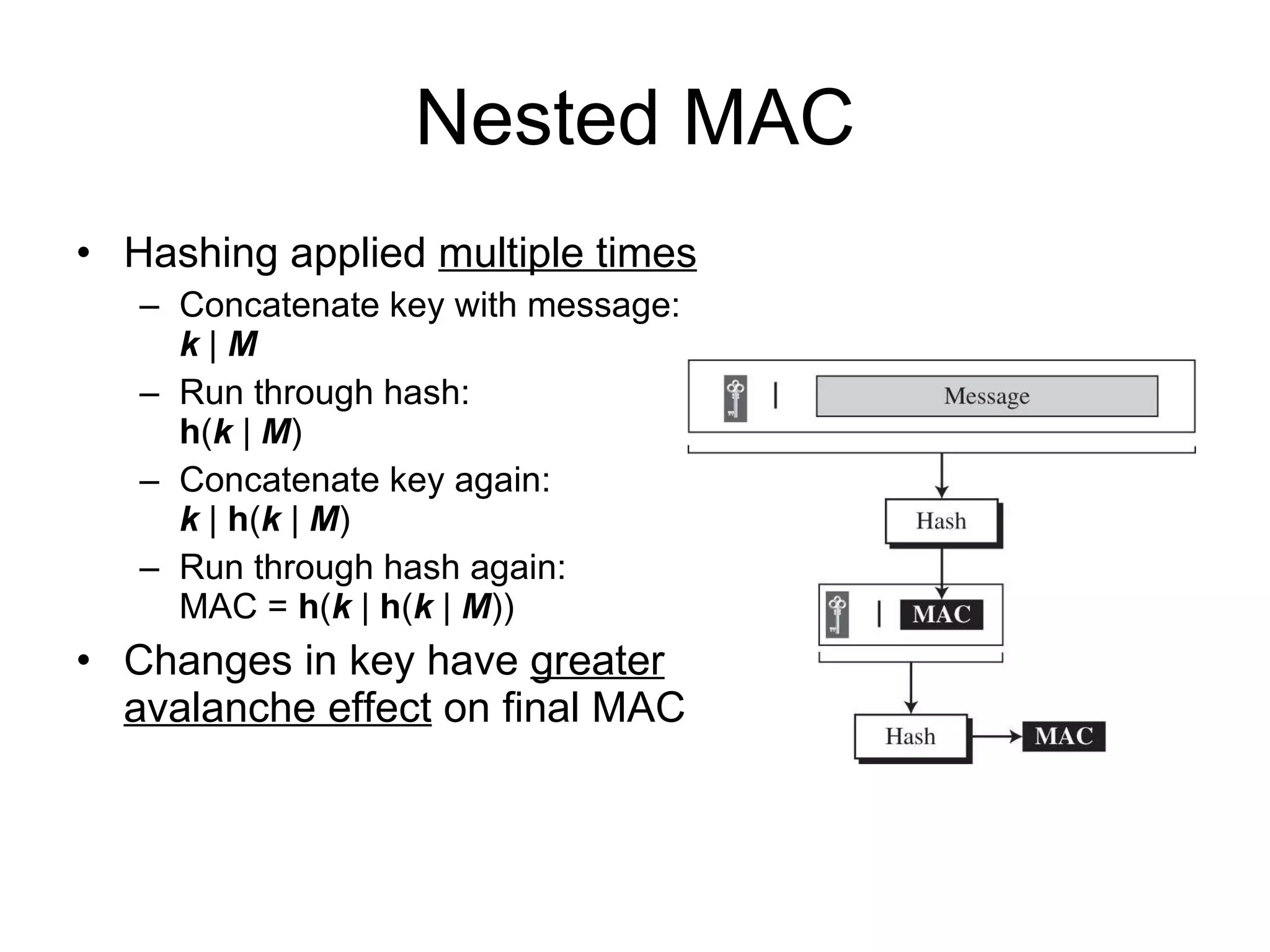
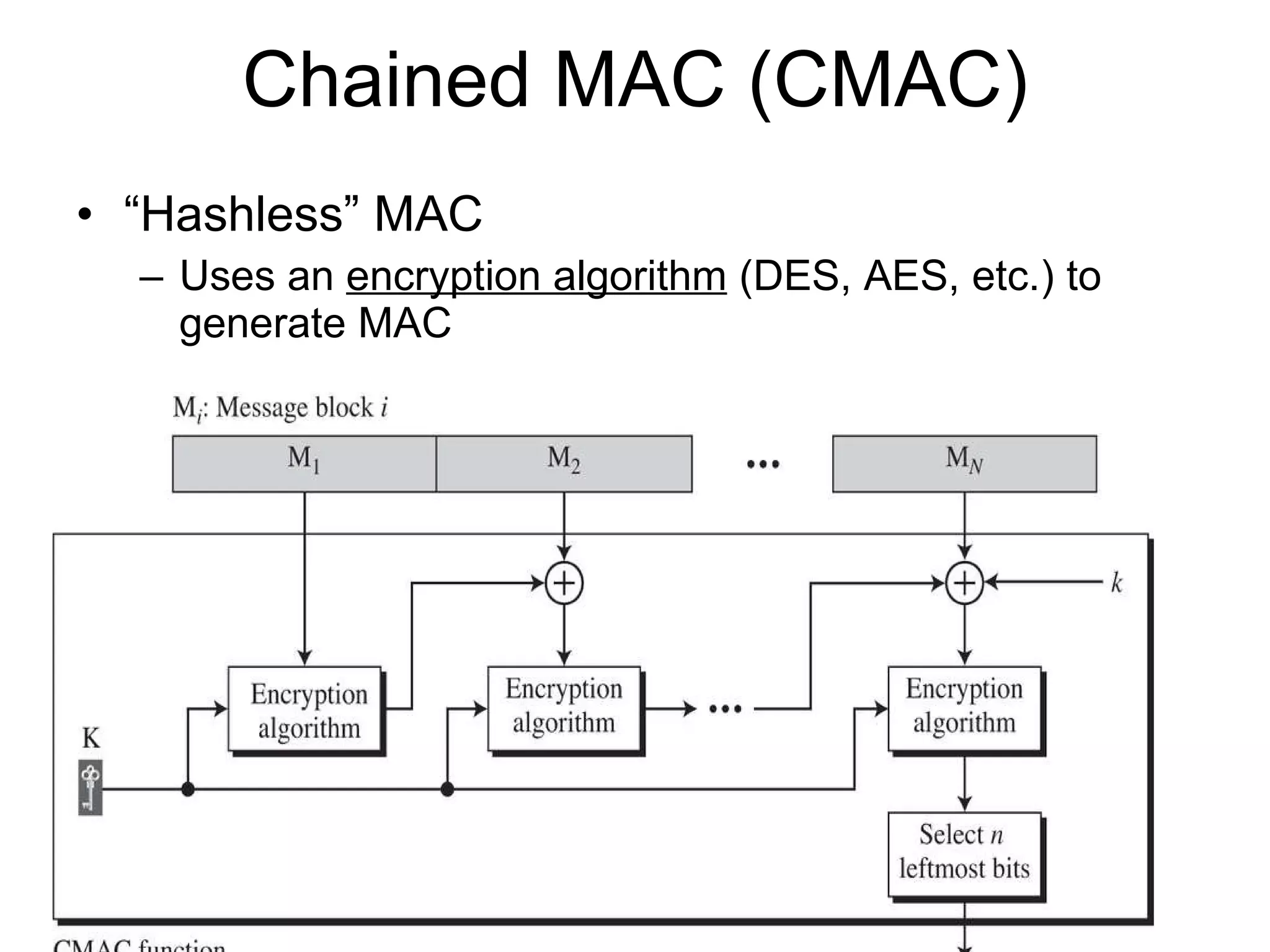
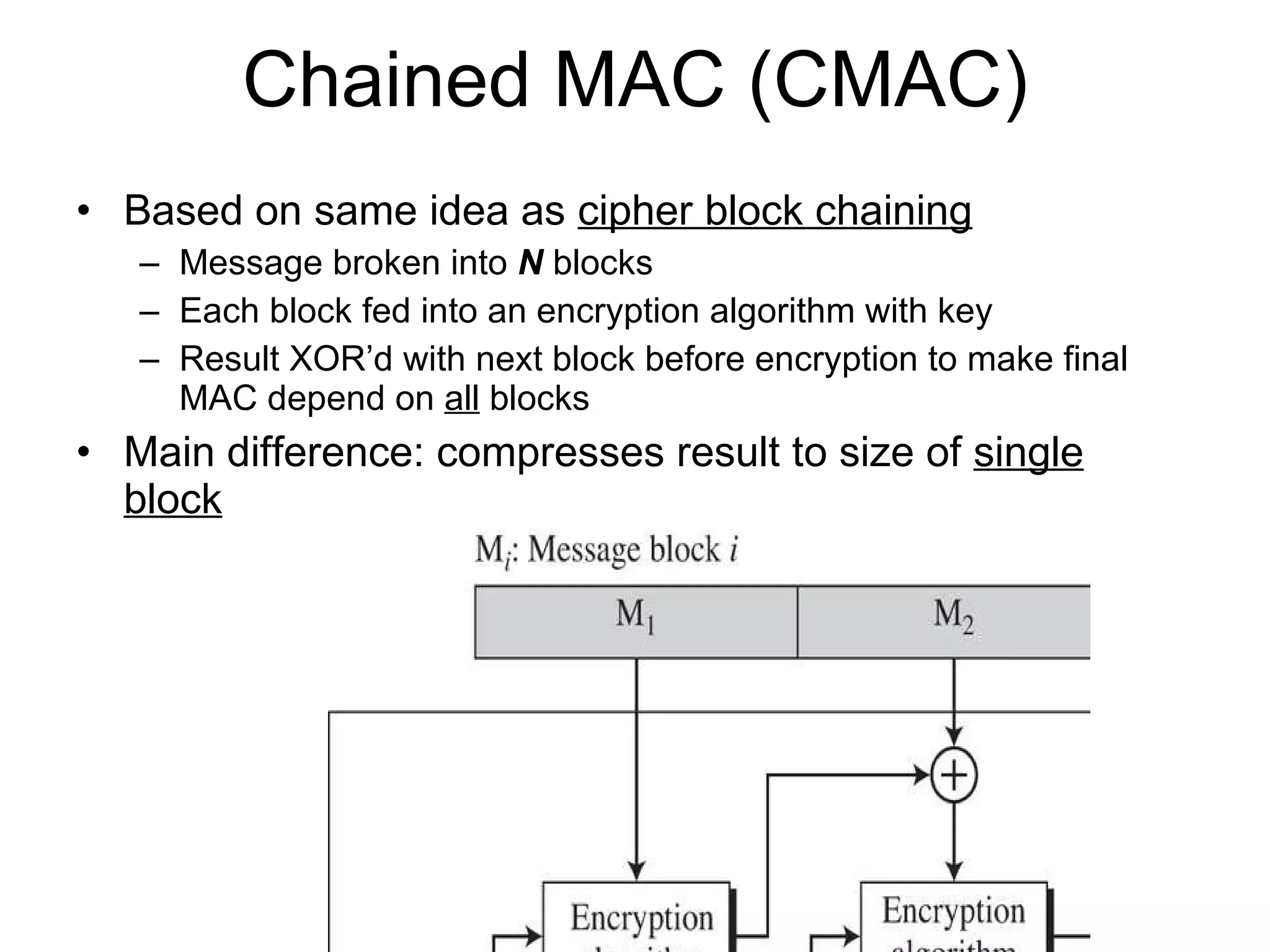
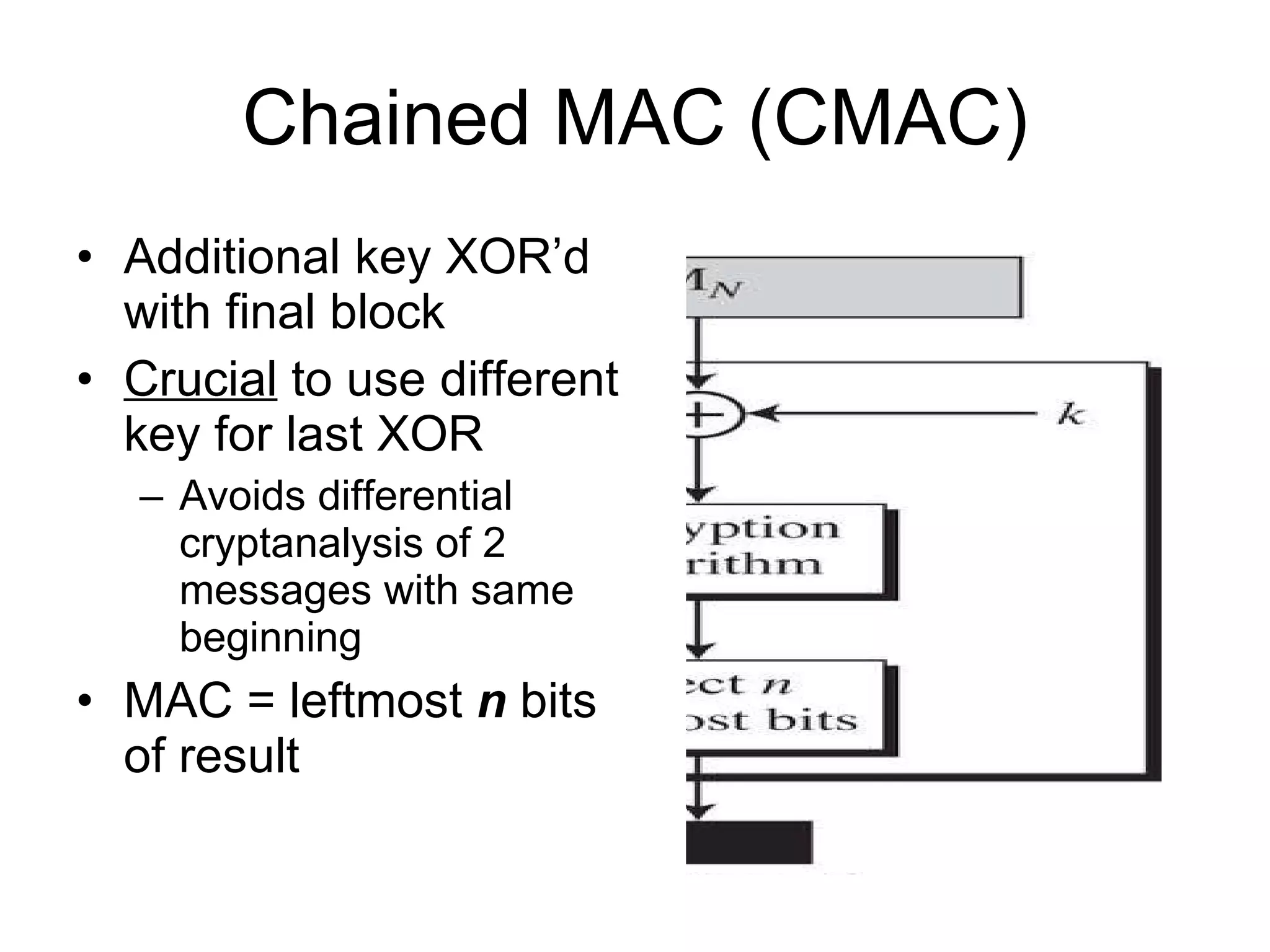
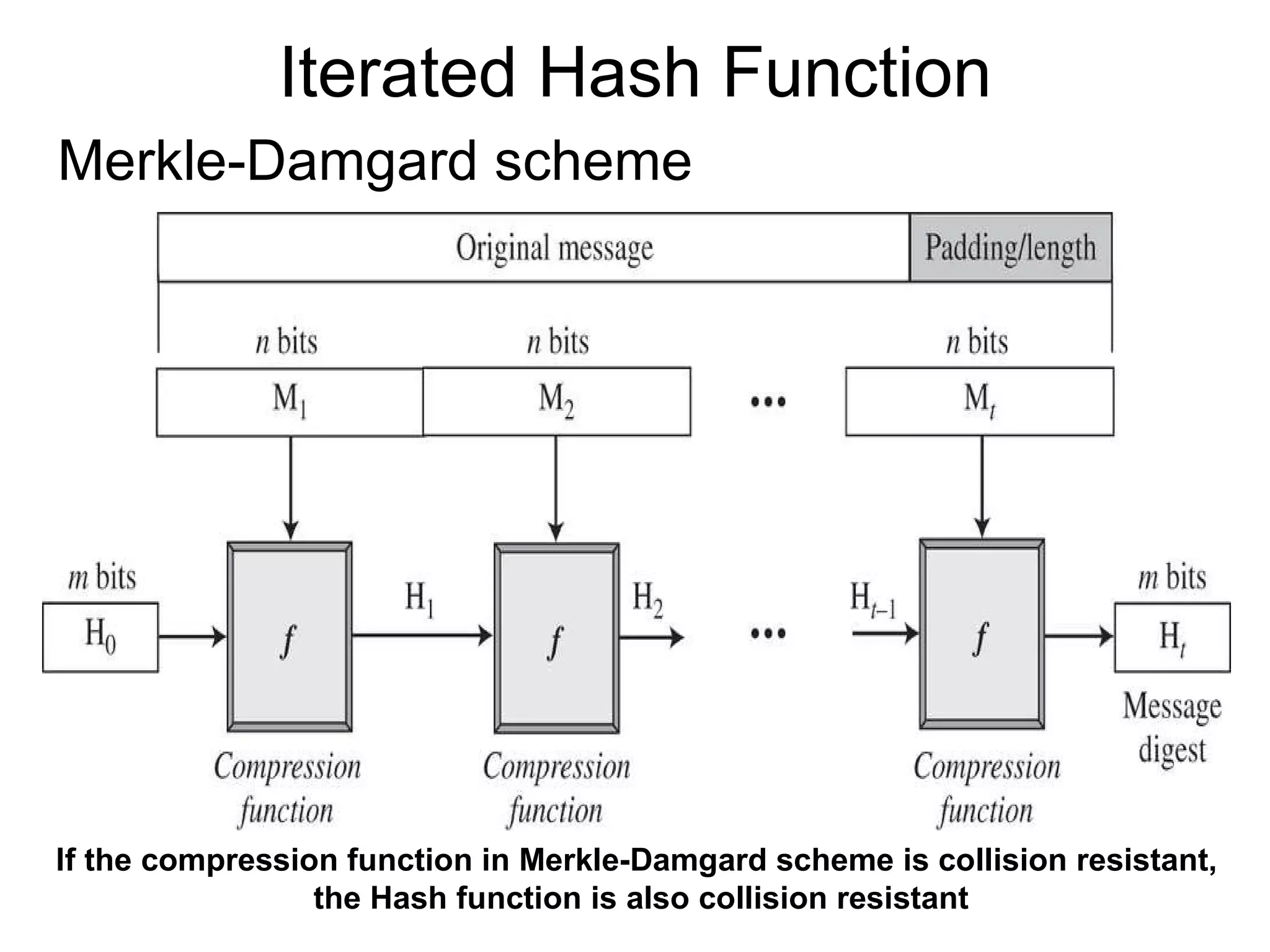
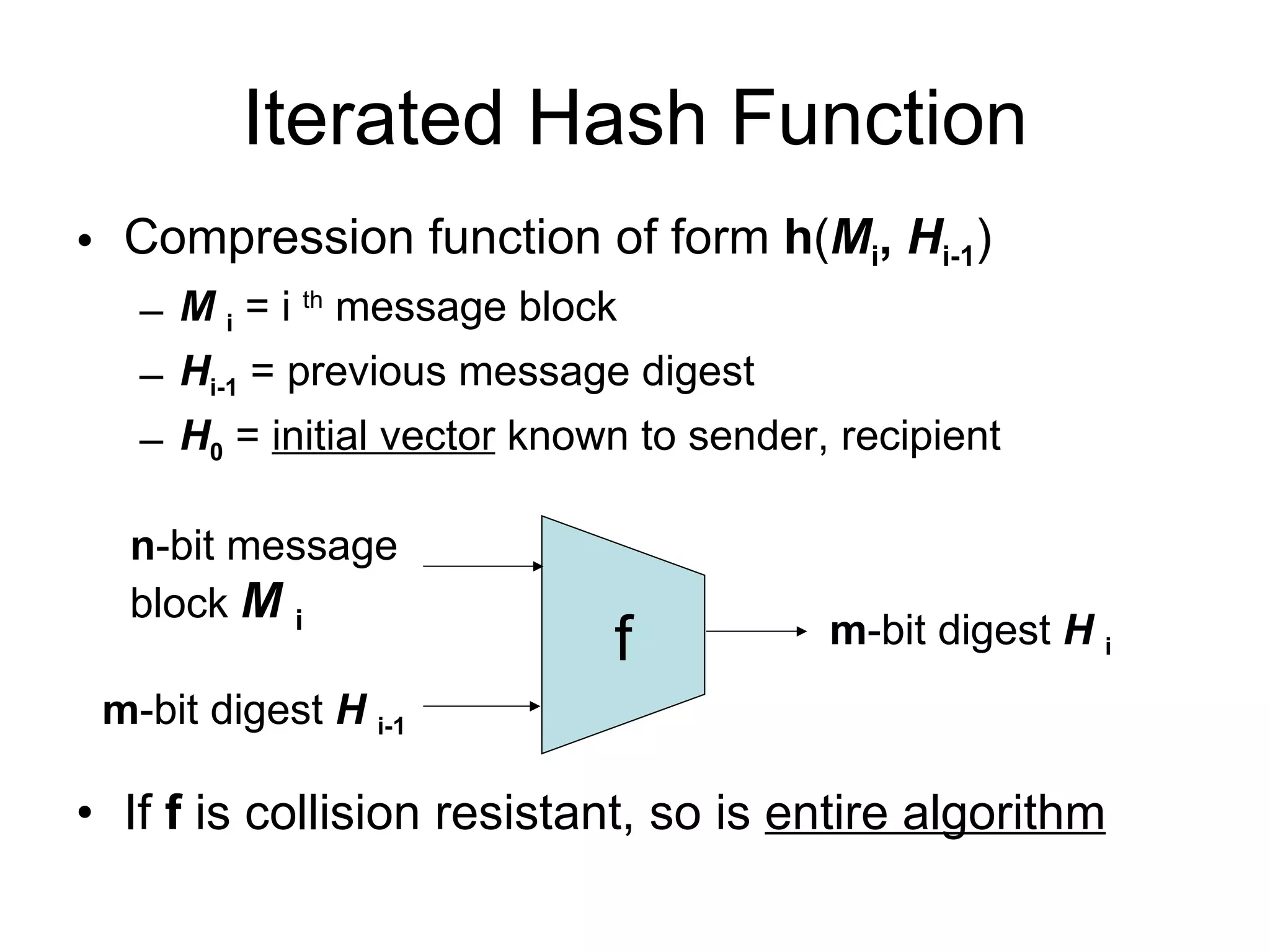
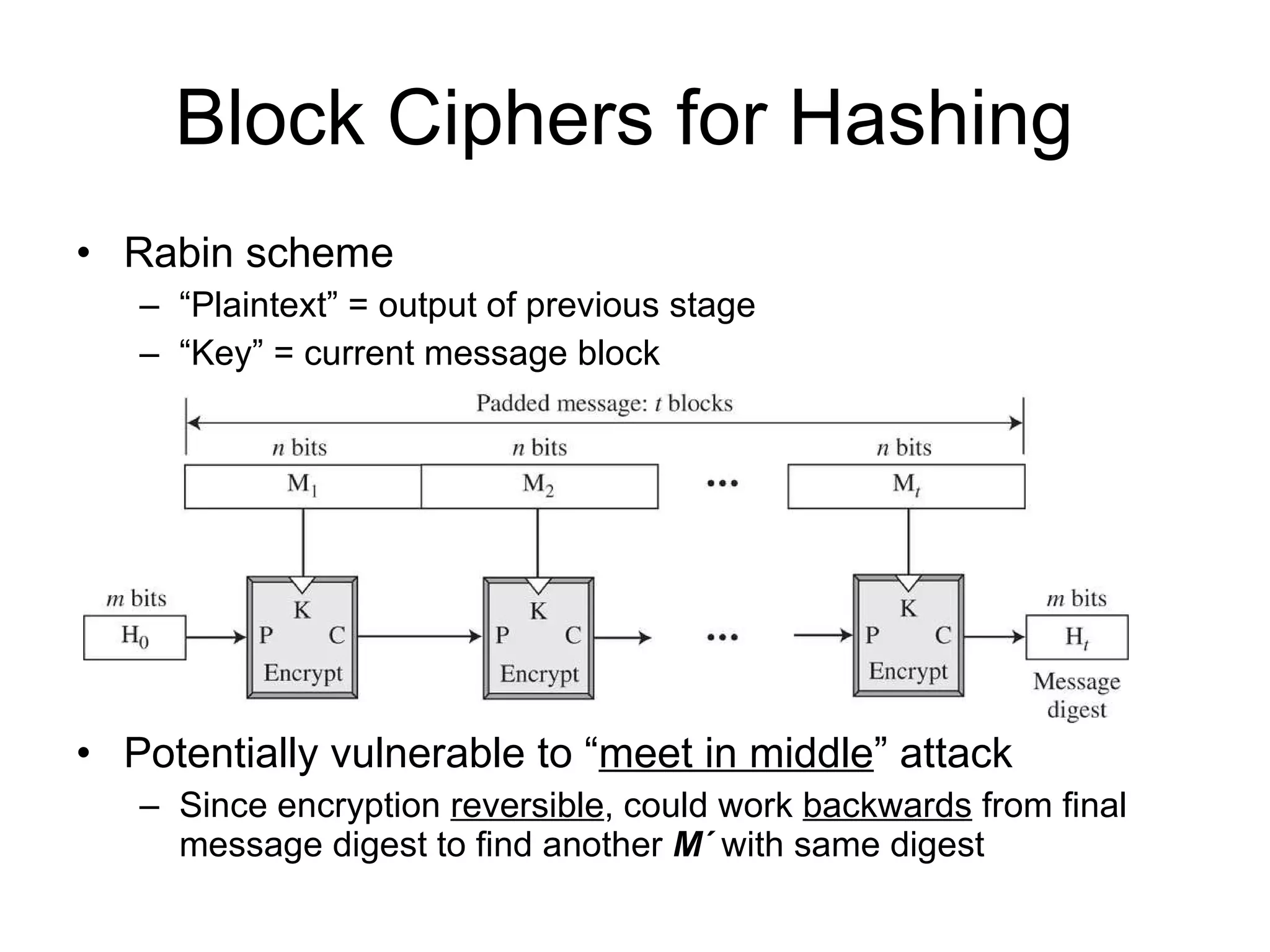
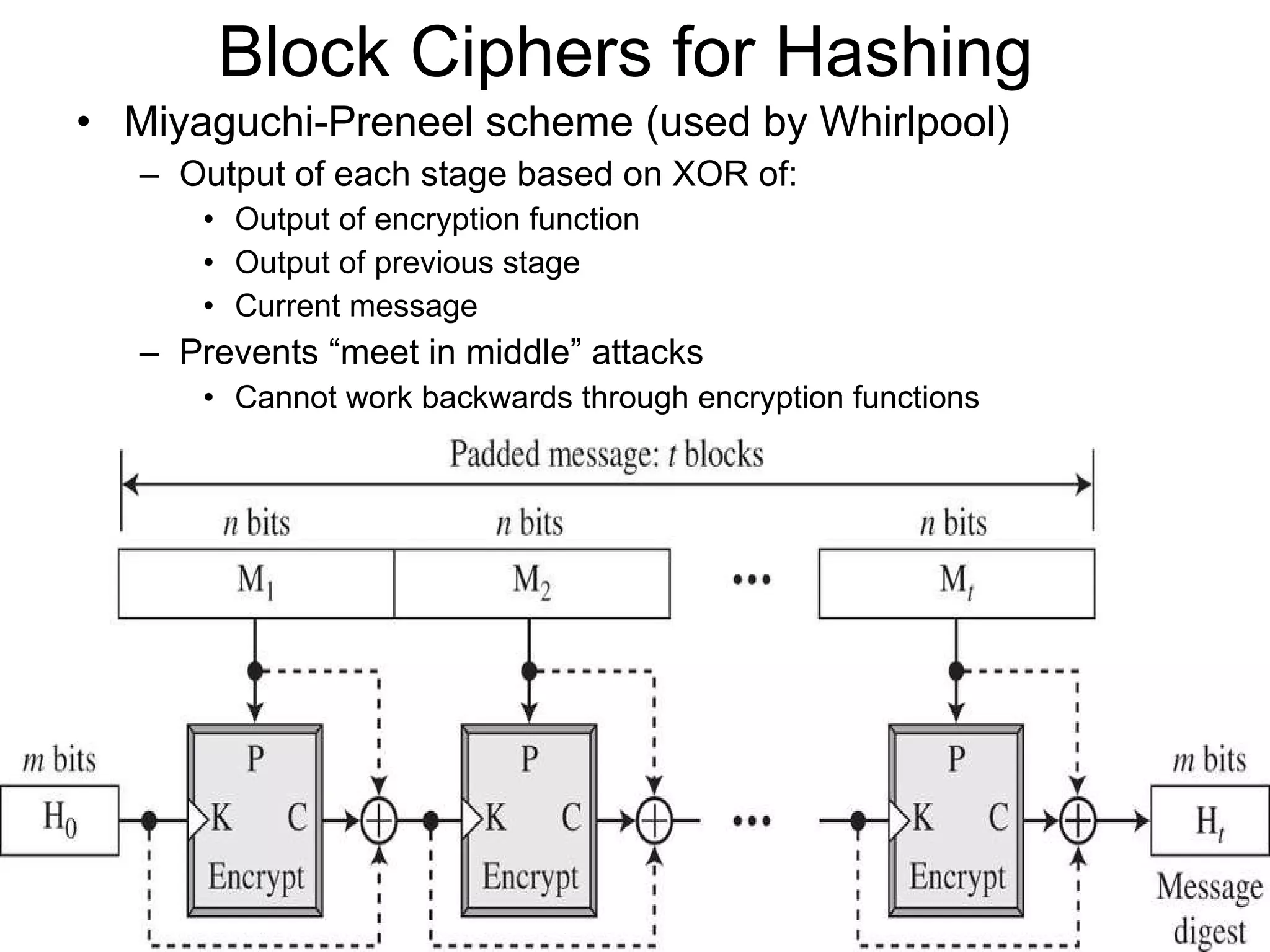
The document discusses network security and techniques for providing message authentication and integrity, including message digests, message authentication codes, and hash functions. It describes how message digests and MACs can detect modifications to messages and prevent masquerading by using secret keys. It also covers attacks like preimage attacks and collision attacks that aim to undermine these integrity protections.

1. Network Security Lecture 5

2. Public Key Cryptography and messae authentication Message authentication codes and hash function to provide message authentication. Public Key encryption and two specific public-key algoritihms. Public-Key encryption to produce digital signatures.

3. Information Integrity Problems Content Modification : Adversary inserts/modifies/deletes message content Insert new record for Darth’s salary of $1,000,000 Salary Database E D E

4. Information Integrity Problems Masquerade : Adversary sends message claimed to be from someone else Masquerading as Alice “ Give Darth a $10,000 raise -- Alice” E

5. Information Integrity Problems Timing Modification Adversary intercepts message and replays it later “ Open the front gate. -- Alice” E

6. Information Integrity Problems Simplest case: Detecting modification Message M stored in public location M not encrypted How can we prove/detect whether adversary has replaced message M with fake message M ´ ? Public storage M M ´

7. Information Integrity Problems One solution: store protected copy of M Compare M to copy to detect changes Implausible if M very large Public storage M M

8. Message Digest Created from message M using hashing function y = h ( M ) Like “ fingerprint ” for messages Different messages  different fingerprints Much more compact than messages: size of y < size of M Plausible for secure storage

9. Message Digest Same concept as error detection in network transmission Error detection bits = function of message Example: parity bit depends on even/odd of 1’s in message If error detection bits do not match message, request message resend Key difference: Unlike noise, adversary intelligent Message Error detection bits

10. Modification Detection Code: MDC Used to detect modification Apply hash to message in storage to get h( M ´ ) Compare with stored h( M ) If h( M’ )  h( M ) message has been modifed Modification Detection Code (MDC) Public storage M ´ h( M ´ ) h compare h( M )

11. Message Authentication Code:MAC Hash applied to message by sender and recipient If no match , message has been tampered with Problem: Requires MDC sent securely Otherwise, adversary could modify it as well!

12. Message Authentication Code Using secret key to prevent adversary from creating message digest to match false message Creates MAC as h ( M , k ) Can also encrypt message , but not necessary

13. Solving Integrity Problems Content Modification If adversary modifies message, will no longer match message digest Authentication Adversary cannot send false message since cannot generate corresponding digest Timing Modification Sender can add timestamp to message which adversary cannot modify without generating corresponding message digest

14. Preimage Attack Adversary finds message M ´ with same MDC h( M ´) = h( M ) Impossible to detect or prove changes! Public storage M ´ h( M ´ ) h Same! h( M )

15. Preimage Attack Adversary can “tweak” new message M ´ until h( M ´) = h( M ) Example: Give Darth a salary increase of $1000 Award Mr. Vader some raise … $2000 Present Darth Vader … bonus $3000 … … … $4000 … “ I’ll find some combination of these so they can’t detect the difference!”

16. Collision Attack Adversary finds two messages M 1 and M 2 with same MDC h( M 1 ) = h( M 2 ) M 1 is harmless message “We like kittens” M 2 has advantage for adversary “Give Darth a $5000 raise”

17. Collision Attack Darth gets job in organization Presents M 1 to boss for approval Boss stores h( M 1 ) Darth actually stores/sends M 2 Boss has no way to prove he didn’t approve M 2 “We like kittens” h( “We like kittens” ) “ Give Darth a $5000 raise”

18. Digests and Networks Same hash applied to message by sender and recipient Sender creates digest and sends along with message Recipient creates digest from received message, and compares to received digest If no match , message has been tampered with en route M 

19. Digests and Networks Problem: Adversary can easily intercept digest and change it to match new message Must assume adversary knows hash function we use! M  h( M  )

20. Message Authentication Codes Using secret key to create digest Creates MAC as h ( M , k ) Without k , adversary cannot substitute M   and then duplicate the h ( M  , k ) that recipient will use to check message integrity

21. Message Authentication Codes Provides authentication of sender Only person with correct key k can produce h ( M , k ) that matches message M Also provides nonrepudiation protection Sender cannot later claim they did not send message unless key stolen M h ( M , k ) h ( M , k ) M h k h ( M , k ) compare “ If they match, then sender must have same key k as I do”

22. Authentication and Confidentiality Can also encrypt message with different key Hash plaintext before encryption Hash ciphertext after encryption Allows authentication to take place without decryption (usually much faster) h h h h h h h

23. Prefix/Postfix MAC Key = “extra bits” at beginning or end of message h ( M , k ) = h ( M | k ) or h ( k | M ) Attack by exhaustive key search : Adversary intercepts M and MAC h ( M , k ) Adversary tries all key values k  to find h ( M , k  ) = MAC Key size must be large enough to prevent this! Hash algorithm used must have “avalanche effect” Changing few bits at beginning/end changes most bits of MAC Better if key “spread out” over message rather than at known fixed location Message

24. Nested MAC Hashing applied multiple times Concatenate key with message: k | M Run through hash: h ( k | M ) Concatenate key again: k | h ( k | M ) Run through hash again: MAC = h ( k | h ( k | M )) Changes in key have greater avalanche effect on final MAC

25. Chained MAC (CMAC) “ Hashless” MAC Uses an encryption algorithm (DES, AES, etc.) to generate MAC

26. Chained MAC (CMAC) Based on same idea as cipher block chaining Message broken into N blocks Each block fed into an encryption algorithm with key Result XOR’d with next block before encryption to make final MAC depend on all blocks Main difference: compresses result to size of single block

27. Chained MAC (CMAC) Final stage uses “additional key” Derived from cipher key but hides relationship to key: Encrypting all 0’s Multiplying by x or x 2 over GF ( 2 n )

28. Chained MAC (CMAC) Additional key XOR’d with final block Crucial to use different key for last XOR Avoids differential cryptanalysis of 2 messages with same beginning MAC = leftmost n bits of result

29. Chained MAC (CMAC) Advantages: Can use existing encryption functions Encryption functions have properties that resist preimage and collision attacks Ciphertext designed to appear like “random noise” – good approximation of random oracle model Most exhibit strong avalanche effect – minor change in message gives great change in resulting MAC Disadvantage: Encryption algorithms (particularly when chained) can be much slower than hash algorithms

30. Compression Functions Function that compresses message of arbitrary length to m -bit digest Following must be computationally infeasible: Given message M , find M ´ such that h ( M ) = h ( M ´ ) Finding any M 1 and M 2 such that h ( M 1 ) = h ( M 1 ) Difficult to assure for arbitrary compression f Message of arbitrary size m -bit digest

31. Compression Functions Easier to create function that compresses block of fixed size k > m Break message into blocks of fixed size f k -bit message m -bit digest

32. Iterated Hash Function Merkle-Damgard scheme If the compression function in Merkle-Damgard scheme is collision resistant, the Hash function is also collision resistant

33. Iterated Hash Function Compression function of form h ( M i , H i-1 ) M i = i th message block H i-1 = previous message digest H 0 = initial vector known to sender, recipient If f is collision resistant, so is entire algorithm f n -bit message block M i m -bit digest H i m -bit digest H i-1

34. Types of Hash Algorithms “ Made from scratch” Specifically designed for hashing Often no clear structure for maximum confusion Examples: Message Digest ( MD ) designed by Ron Rivest Secure Hash Algorithm ( SHA ) Based on block ciphers Rebuild existing cipher into compression function Already has desirable properties of cryptographic hash Example: Whirlpool

35. Block Ciphers for Hashing Rabin scheme “ Plaintext” = output of previous stage “ Key” = current message block Potentially vulnerable to “ meet in middle ” attack Since encryption reversible , could work backwards from final message digest to find another M  with same digest

36. Block Ciphers for Hashing Miyaguchi-Preneel scheme (used by Whirlpool) Output of each stage based on XOR of: Output of encryption function Output of previous stage Current message Prevents “meet in middle” attacks Cannot work backwards through encryption functions