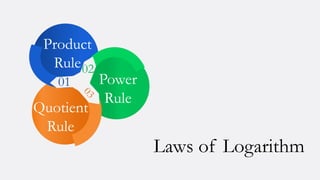
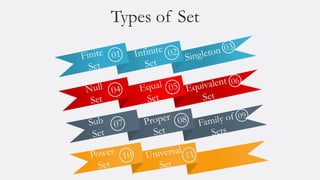
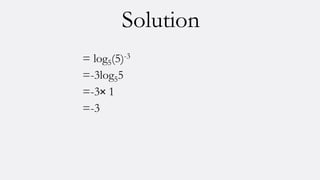Logarithms are exponents that represent the power to which a number must be raised to get another number. There are three laws of logarithms: the product rule states that multiplication becomes addition, the quotient rule states that division becomes subtraction, and the power rule states that exponents become multipliers. Matrices are rectangular arrangements of numbers that can be added, subtracted, multiplied, and have other operations performed on them. There are different types of matrices including identity, inverse, and triangular matrices. Sets are collections of objects that are used to define concepts like relations and functions. Basic set operations include union, intersection, and complement.

1. Logarithm

2. A logarithm is the power to which a
number must be raised in order to
get some other number.

3. Product
Rule
Power
Rule
Quotient
Rule
01
02
Laws of Logarithm

4. Laws of Logarithm
Product rule: Multiplication becomes
addition.
loga(xy) = loga x + loga y

5. Laws of Logarithm
Quotient Rule: Division becomes subtraction.
Loga(x/y) = loga x - loga y

6. Laws of Logarithm
Power rule: Exponent becomes multiplier.
Loga(x)y = y loga x

7. Example
 Find the value for log58 + log5(1/1000)

8. Solution
Log58 + log5(1/1000)
= log5(8×1/1000)
= log5(1/125)
= log5(1/5)3

9. = log5(5)-3
=-3log55
=-3× 1
=-3
Solution

10. Matrix

11. Matrix
Matrix is a rectangular arrangement of numbers.

12. Operations
Of
Matrix
Addition
SubtractionMultiplication

13. Set
Square
Matrix Null
Matrix
Diagonal
Matrix
Identity
Matrix
Scalar
MatrixTriangular
Matrix
Sub
Matrix
Zero
Matrix
Row &
Column
Matrix
Types of Matrices

14. Inverse
Matrix

15. The square matrix A is invertible if there is
a matrix B such that AB = BA =I , where I
is the identity matrix. The matrix B is called
the inverse of A and is denoted by A-1
Inverse Matrix

16. Method
Two methods to find the inverse
matrix.
 Crammer’s Method
 Gauss Method

18. What is Set
Sets are used to define the concepts of relations and
functions. A set is a collection of objects.

19. Georg Cantor
(1845-1918)
History of Set
The theory of set was developed by German
mathematician Georg Cantor.

20. Types of Set

21. Operation on Sets
Intersection
Of
Sets
Union
Of
Sets

22. Suppose there are two sets one is A & the
other one is B.
Union of A and B
Intersection of A and B
A B
A B
A B

23. De- Morgan’s Law
1. Complement of a union is the
intersection of complements.
(AUB) =A B
2. Complement of an intersection is the union of
complements.
(A B) =AUB

24. THE
END