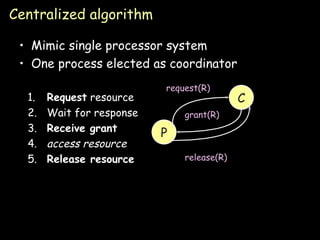
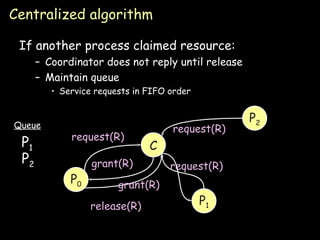
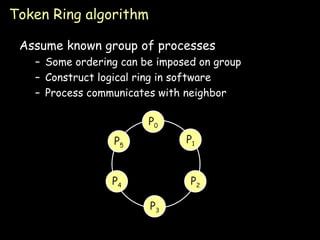
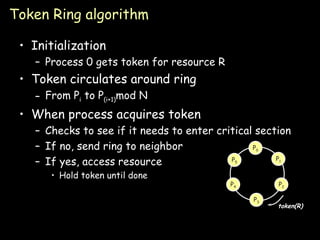
The document discusses several algorithms for process synchronization and mutual exclusion in distributed systems: - Token ring algorithm passes an exclusive token around a logical ring of processes to control access to shared resources. - Ricart-Agrawala algorithm uses message ordering and timestamps to elect a process to enter the critical section. - Lamport's mutual exclusion algorithm uses request queues and timestamps to ensure only one process is in the critical section at a time. 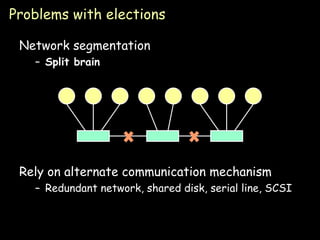- Election algorithms like the Bully and Ring algorithms elect a coordinator process to handle synchronization and recovery from failures.

1. Mutual Exclusion & Election Algorithms Paul Krzyzanowski [email_address] [email_address] Distributed Systems Except as otherwise noted, the content of this presentation is licensed under the Creative Commons Attribution 2.5 License.

17. Election algorithms

24. The end.