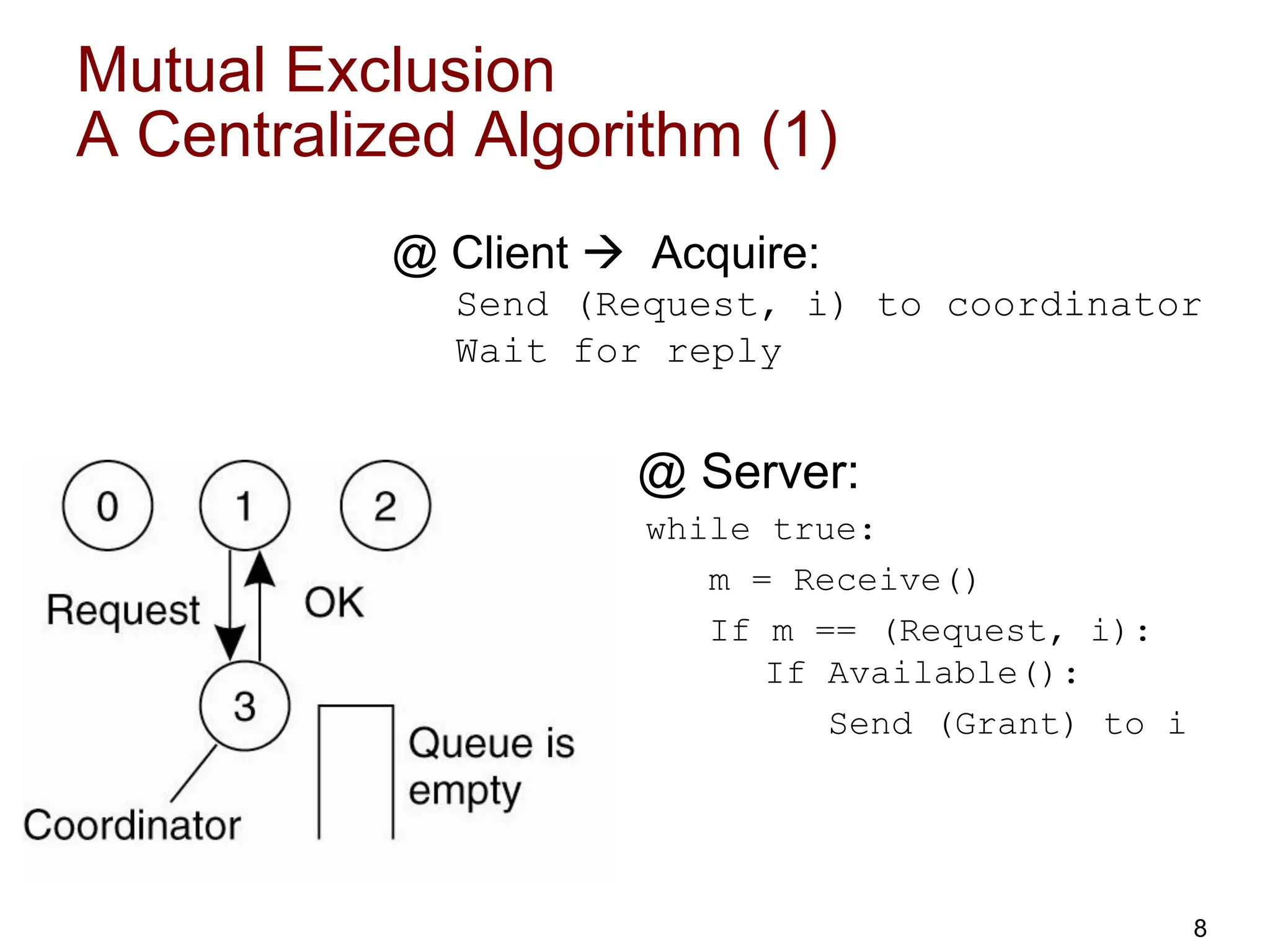
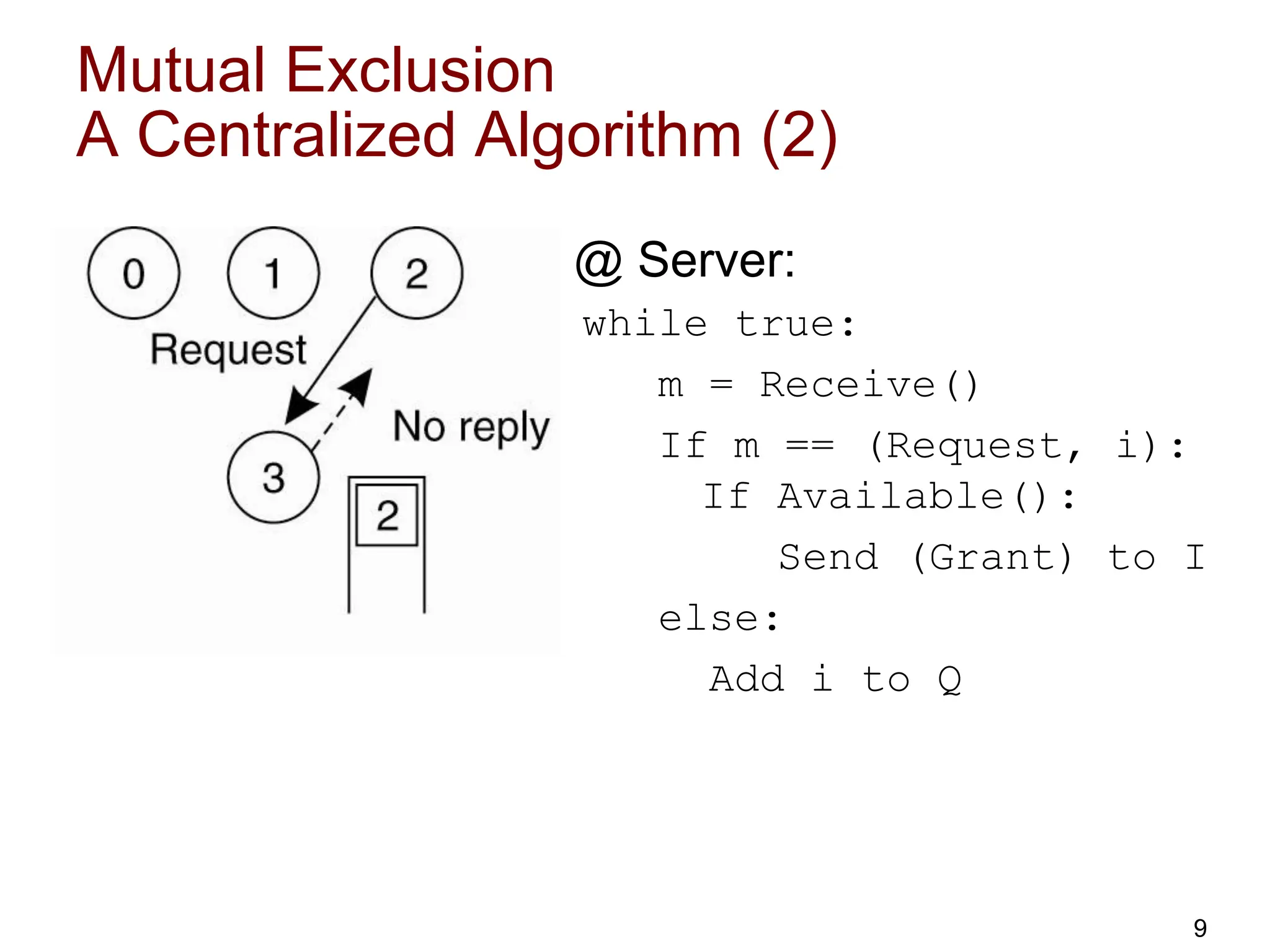
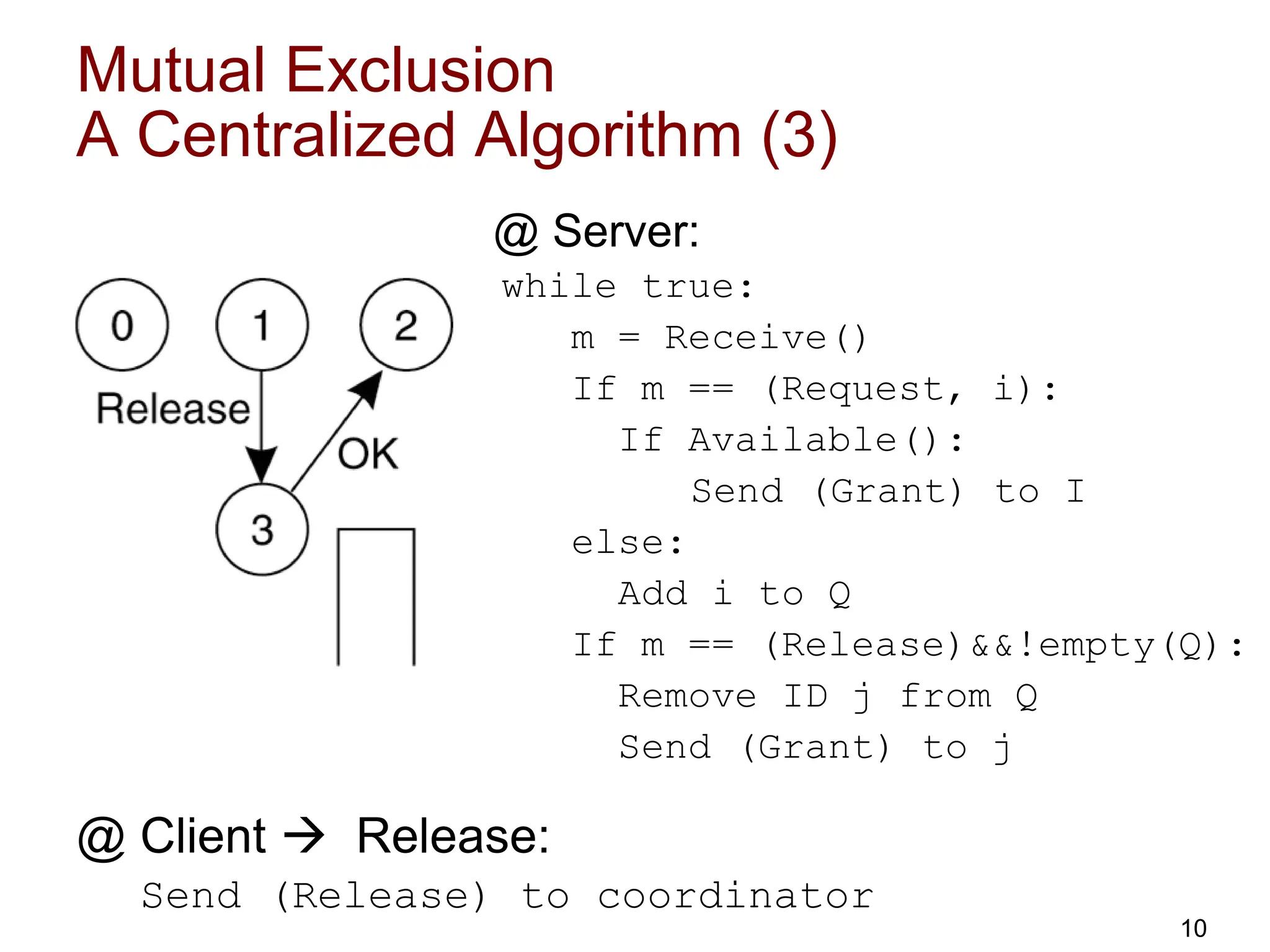
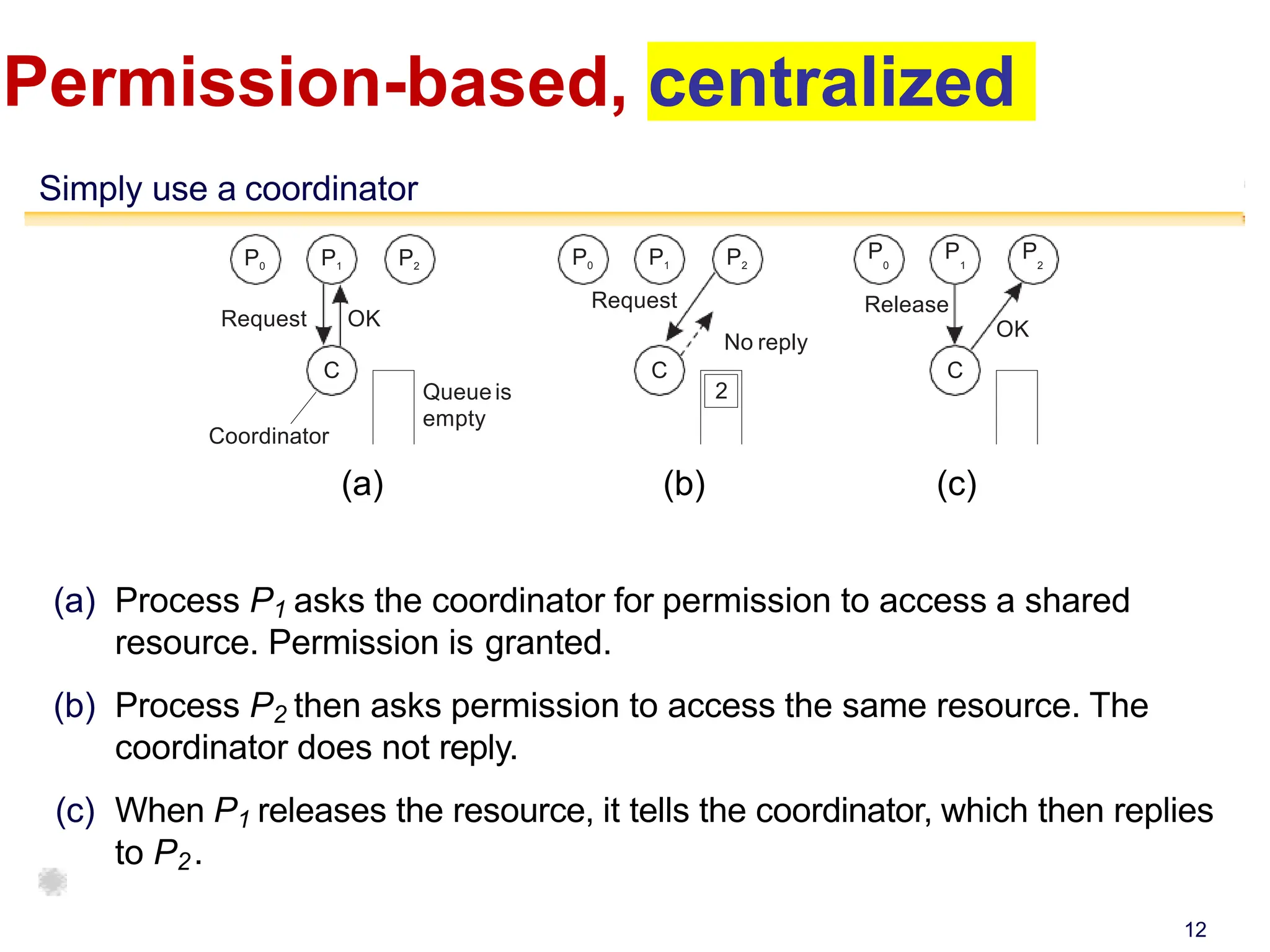
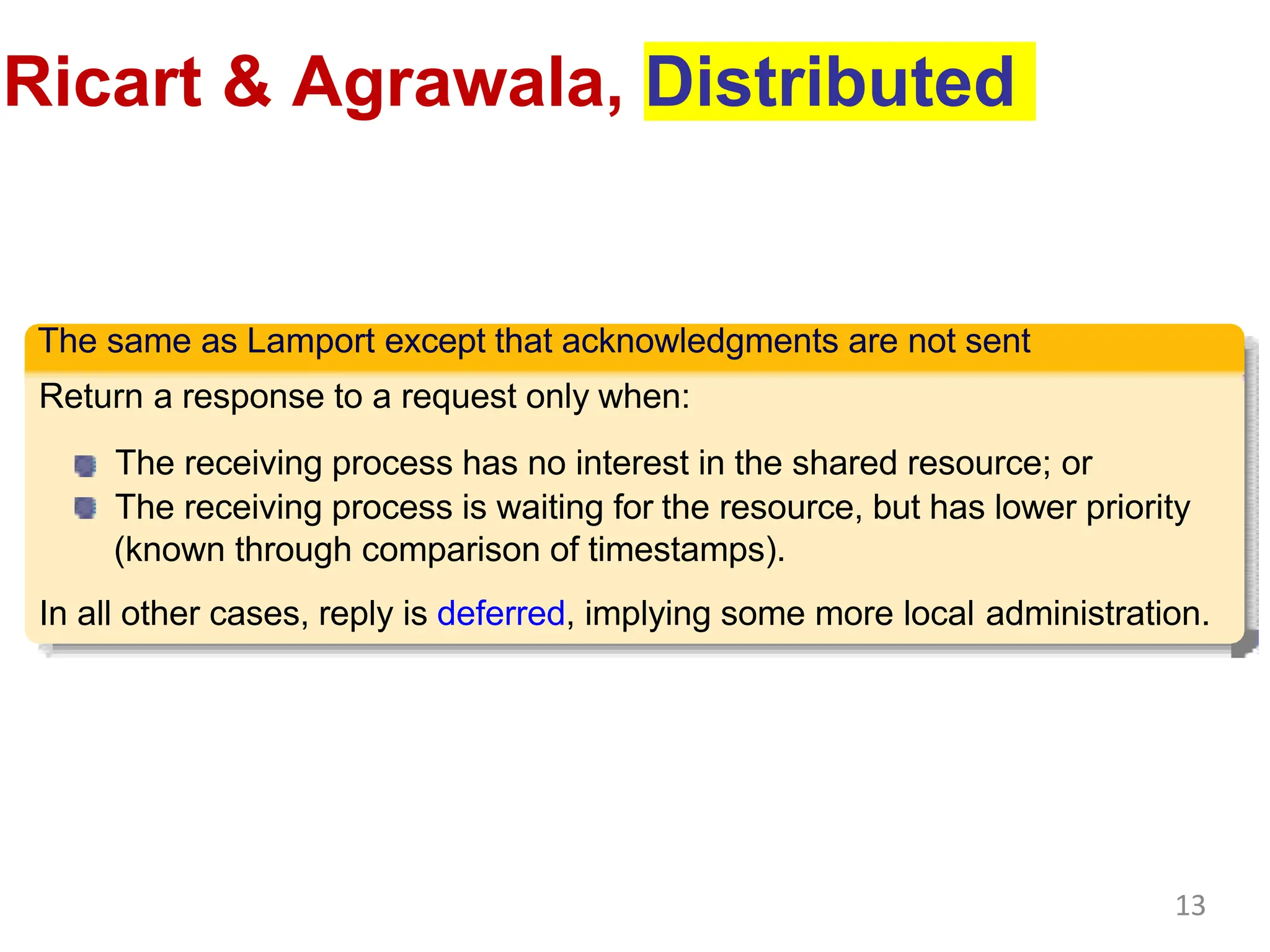
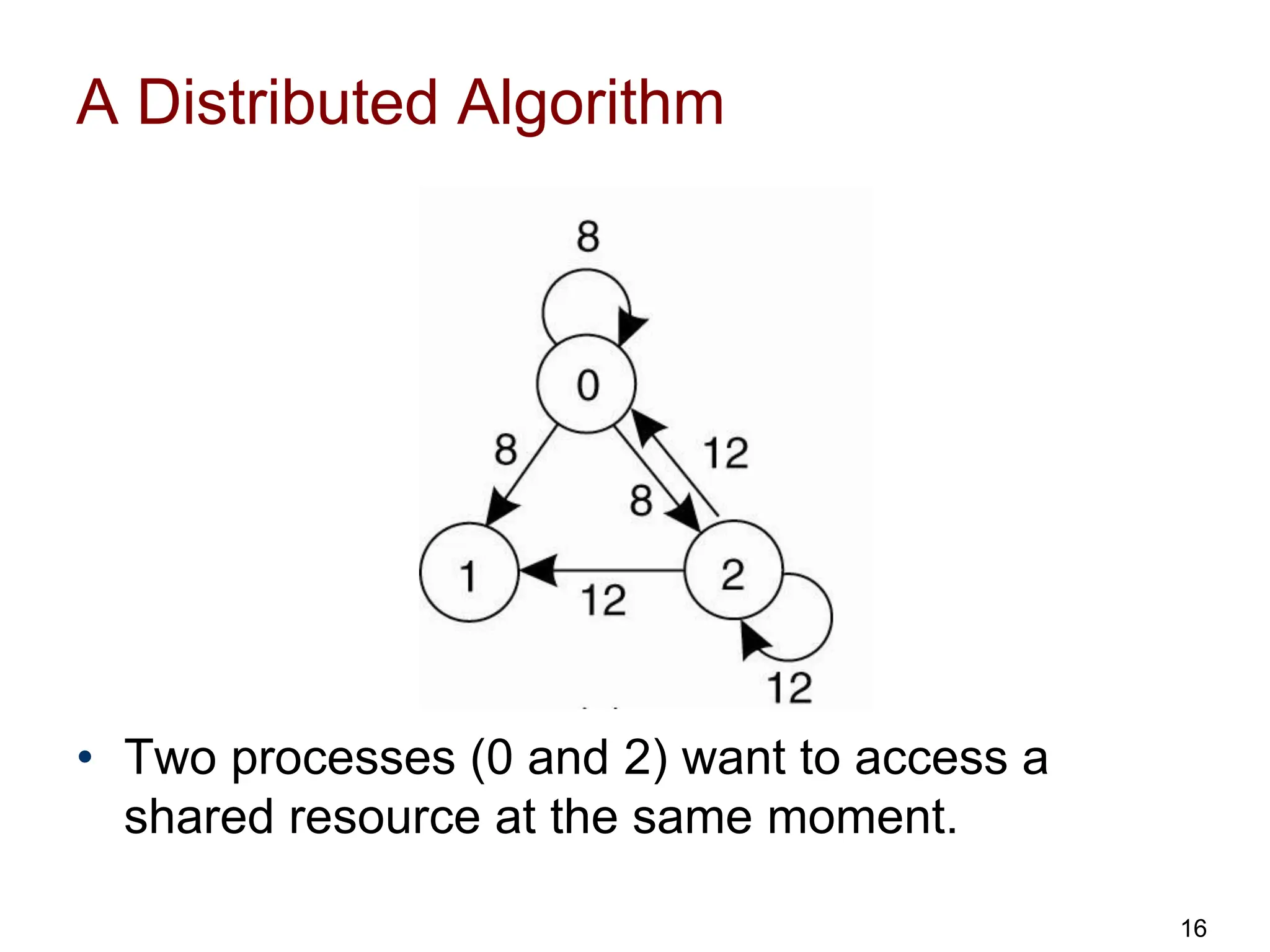
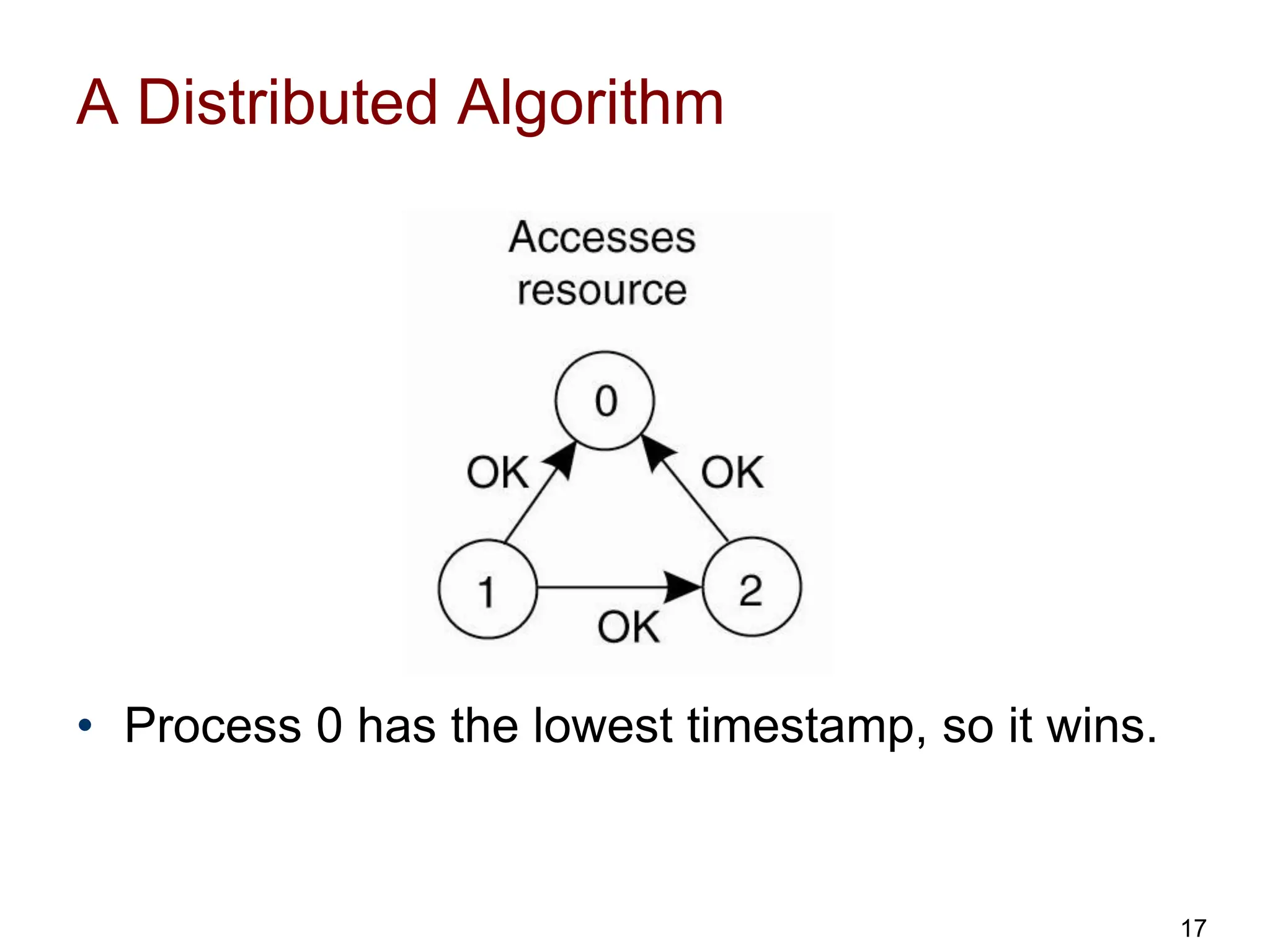
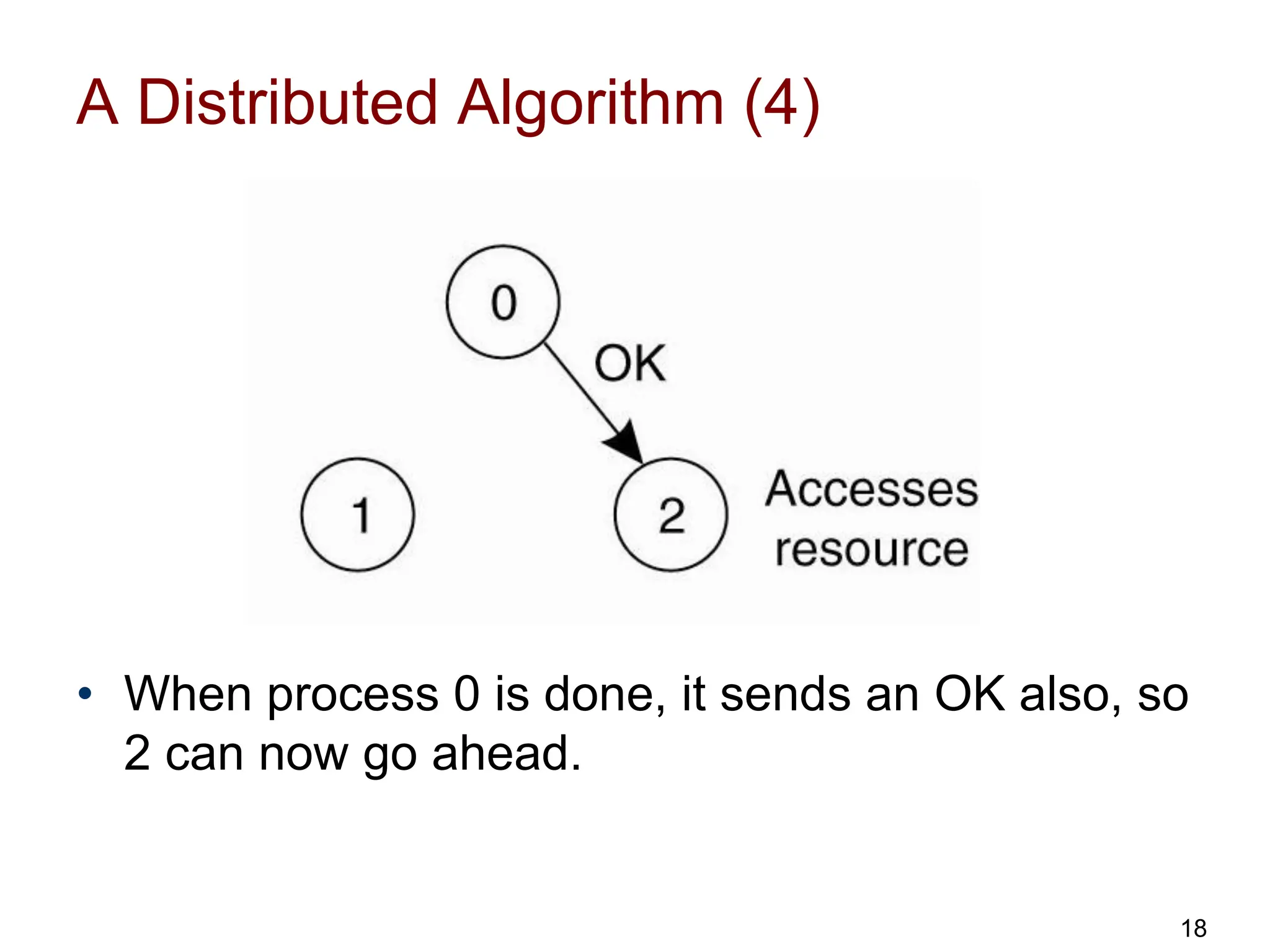
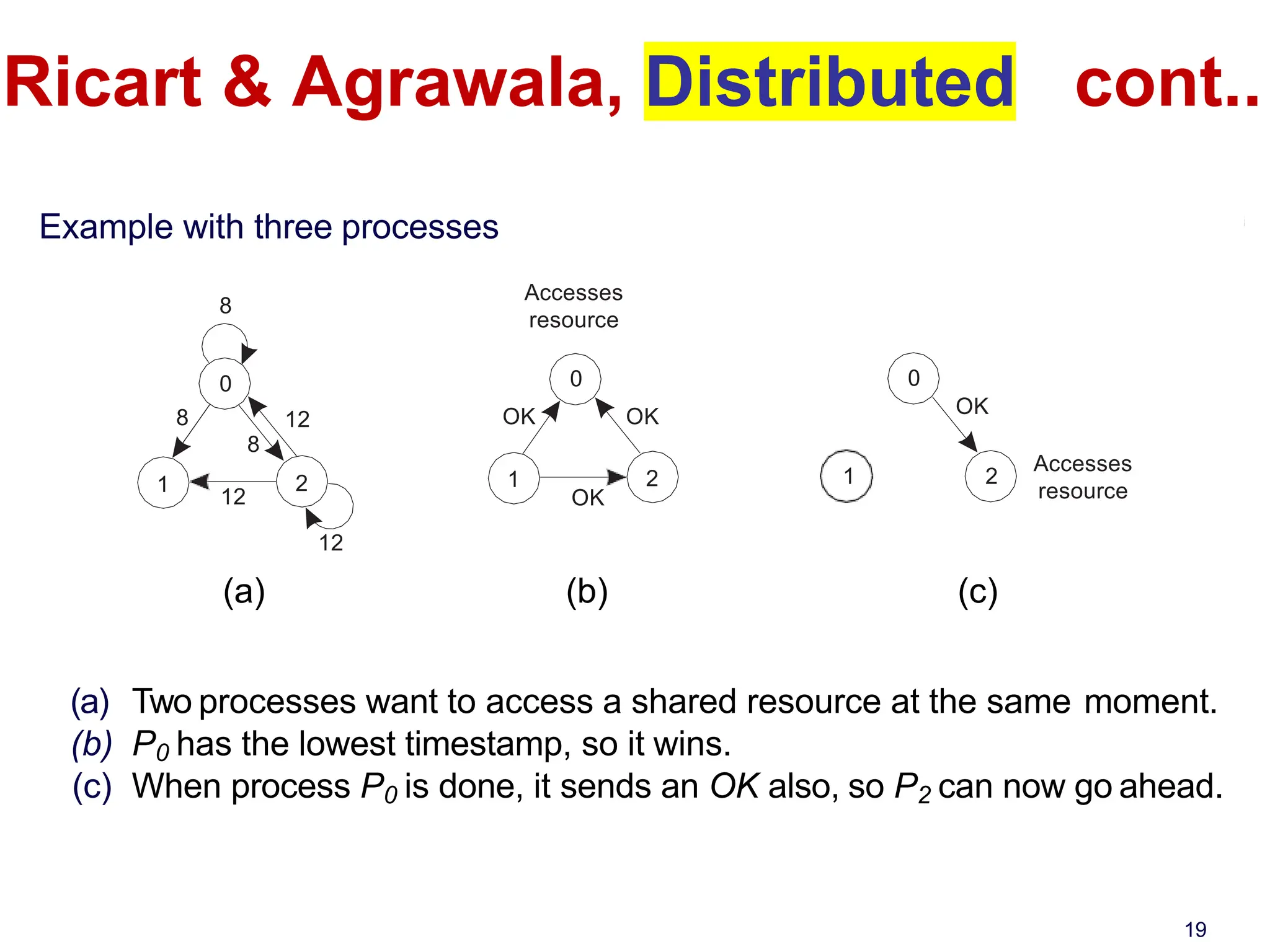
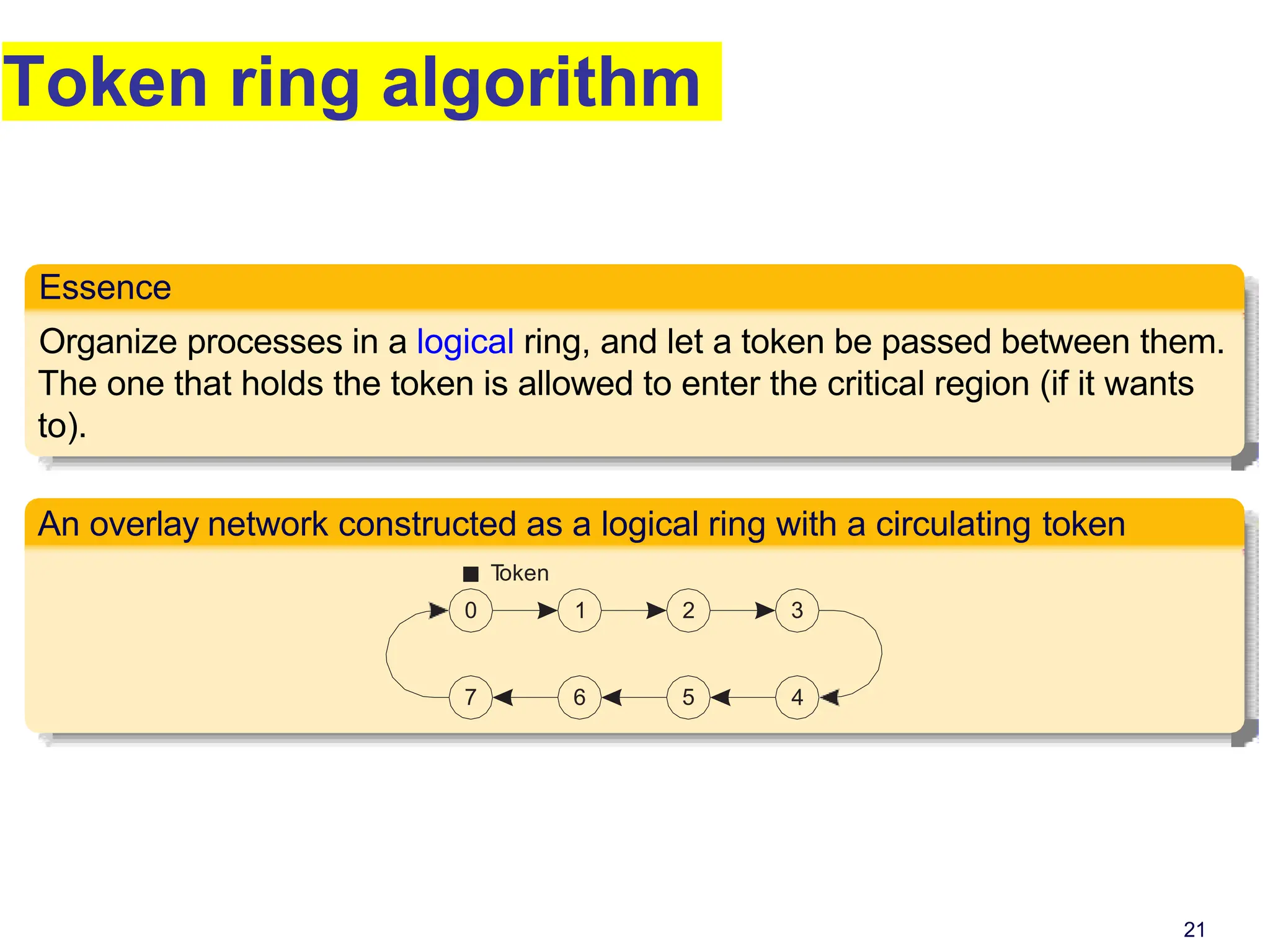
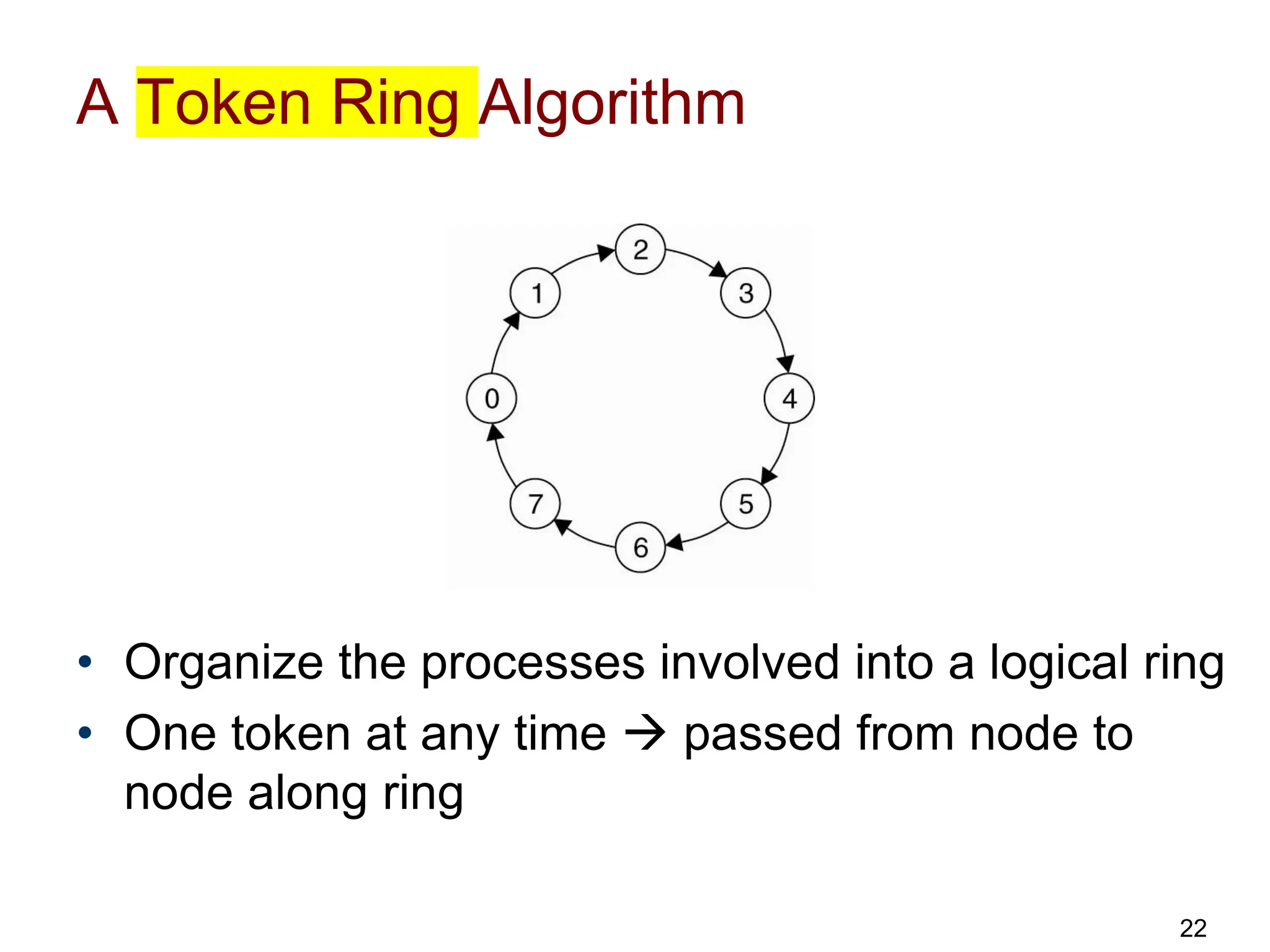
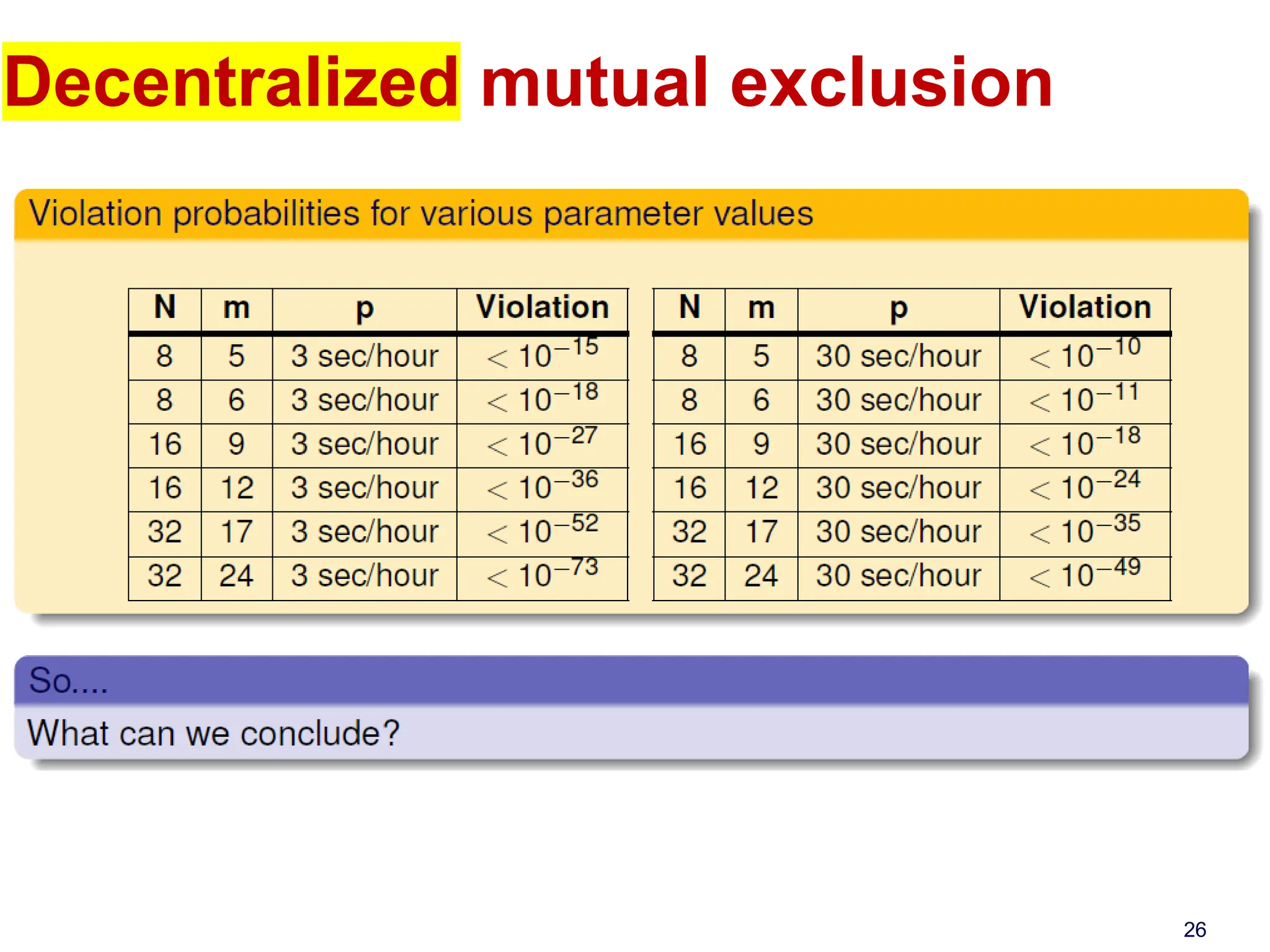
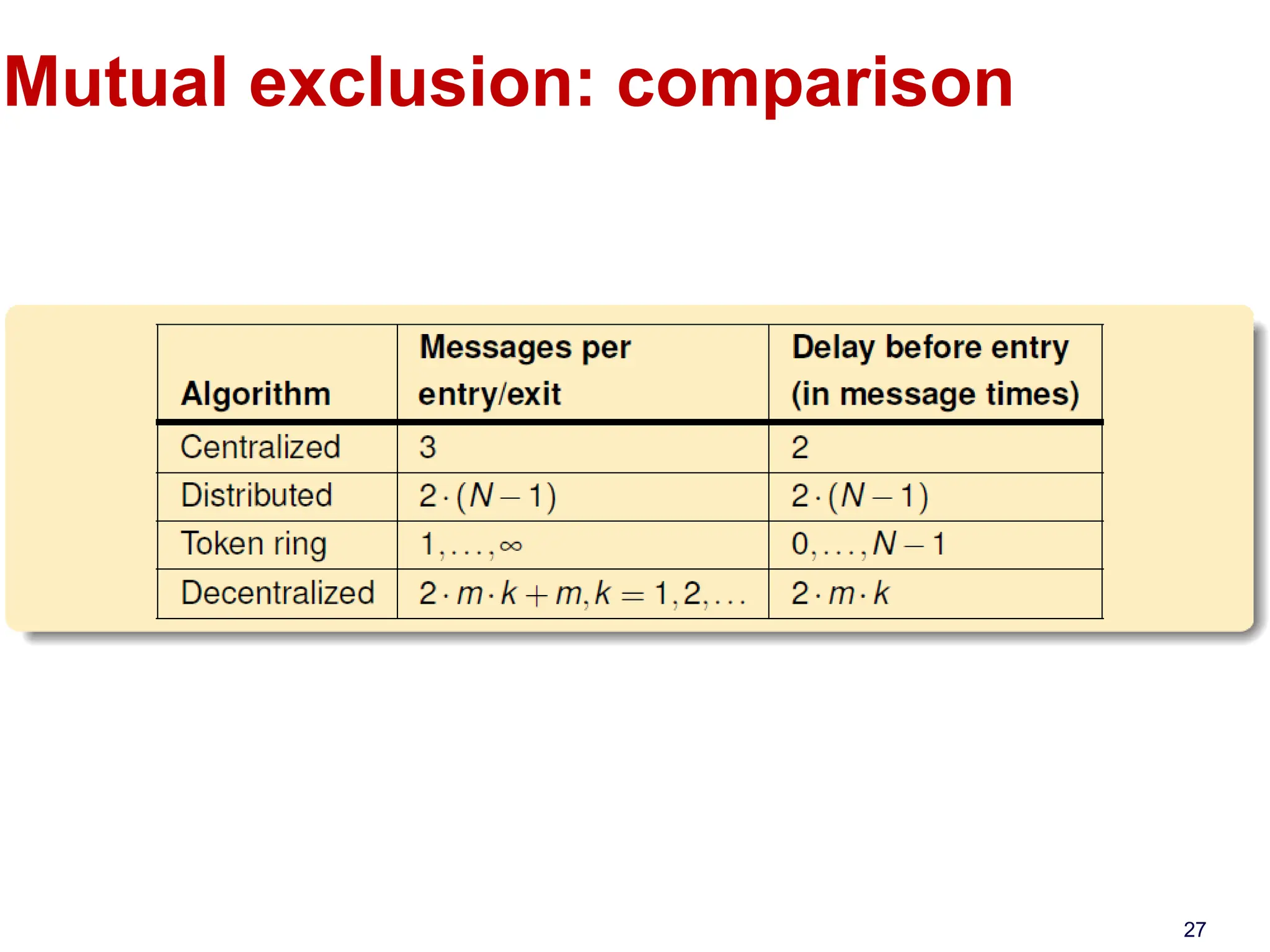
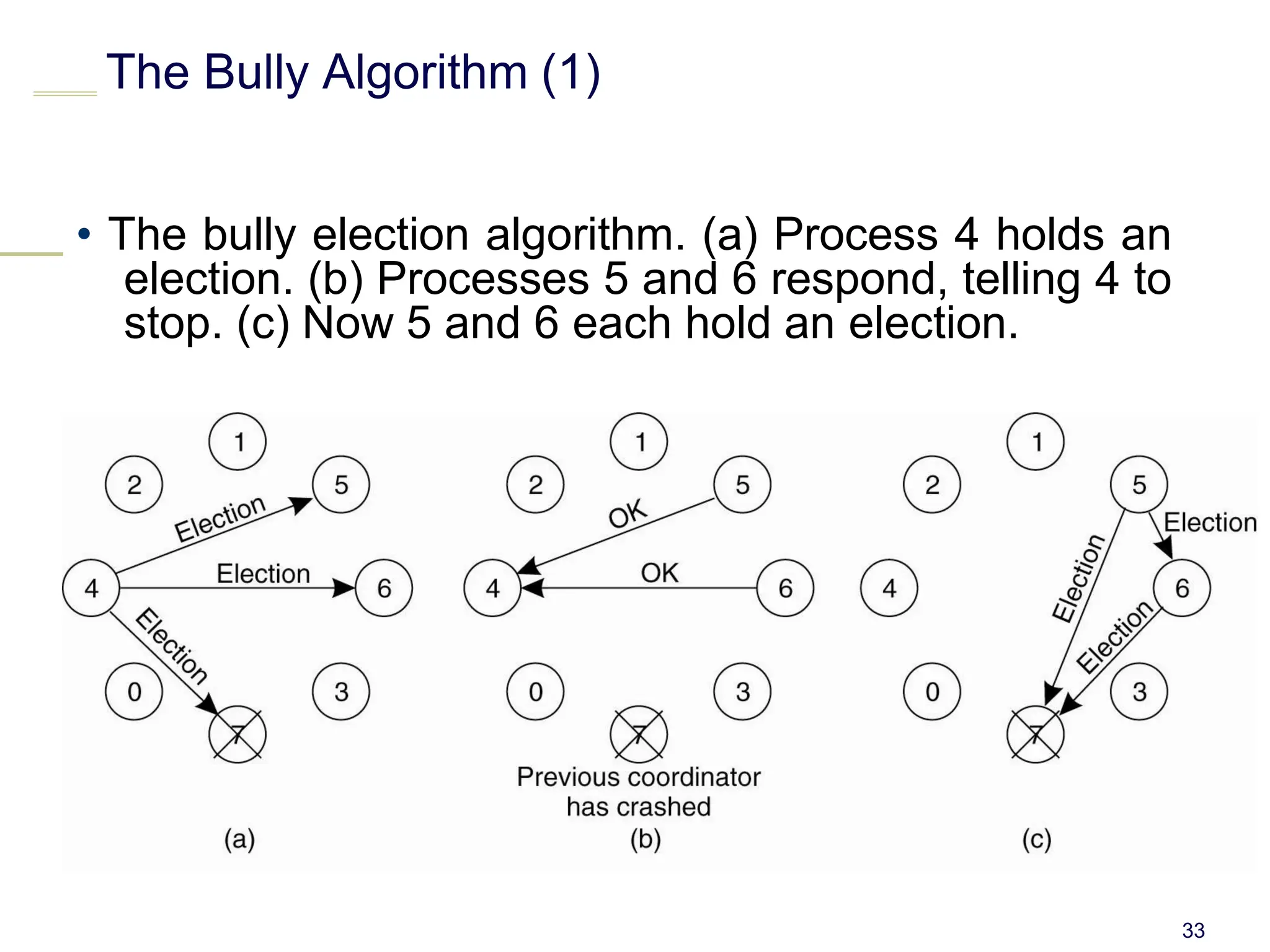
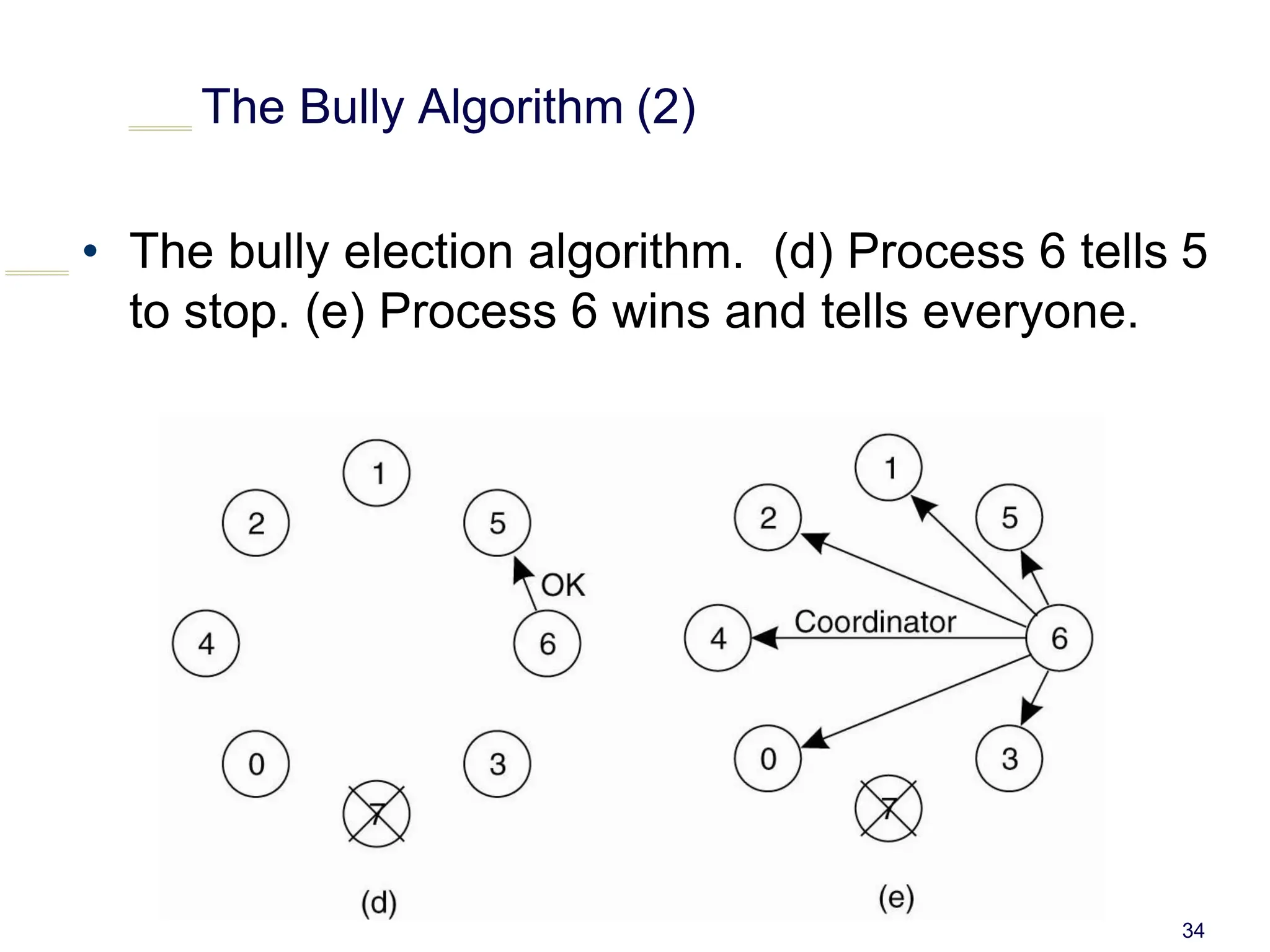
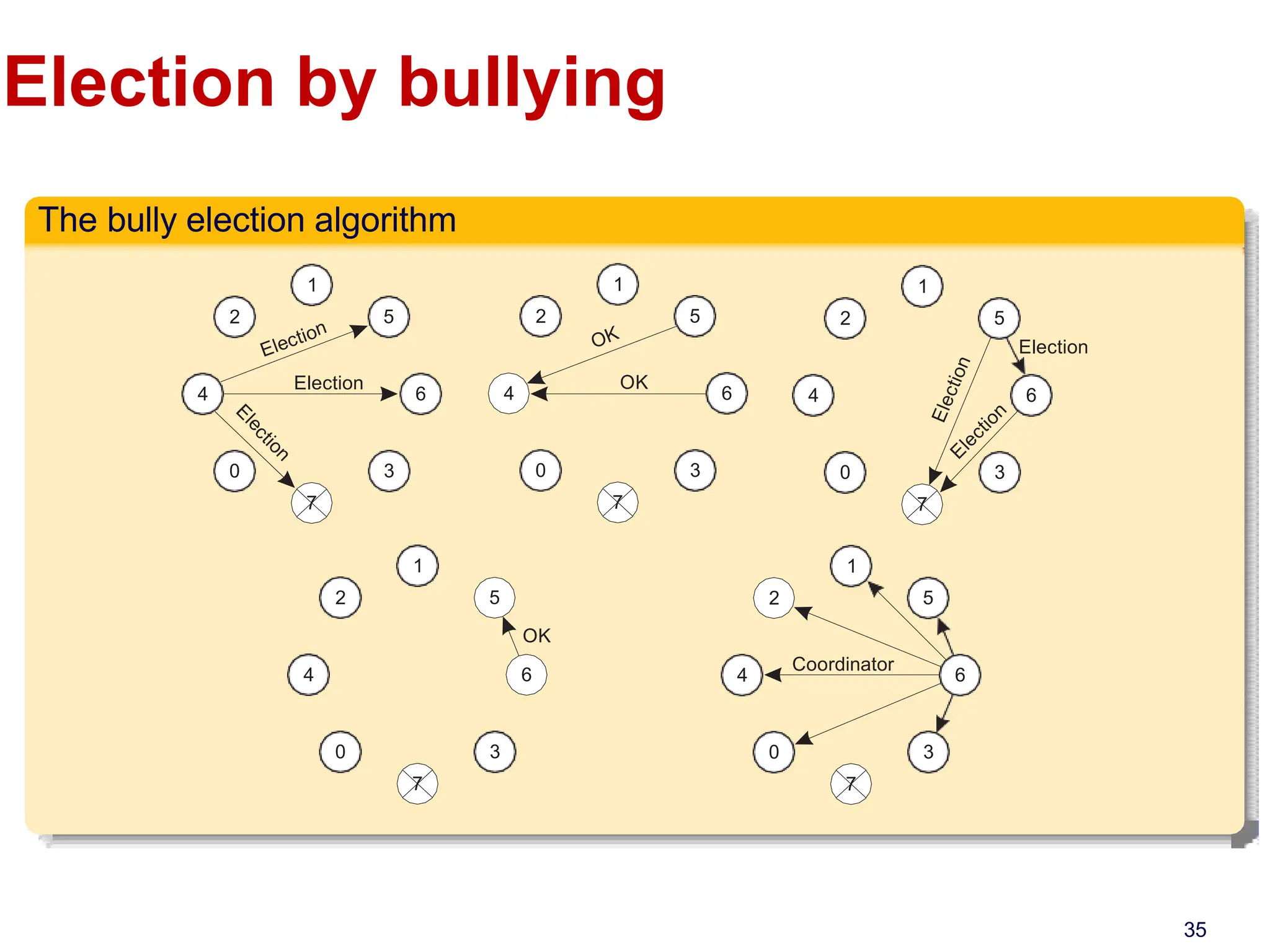
This document discusses algorithms for mutual exclusion and election in distributed systems. It covers centralized and distributed mutual exclusion algorithms including Ricart & Agrawala and token ring. It also covers two election algorithms: the bully algorithm where processes "bully" others to become coordinator, and a ring-based algorithm where processes are organized in a logical ring.

1. Lecture 4 and 5: Mutual Execution and Election
Algorithms
Distributed and Cloud Computing
Fall 2021
Slides adopted from the instructional material of the textbook
Distributed Systems: Principles and Paradigms by Andrew S. Tanenbaum, Maarten van Steen.
1

2. Contents
• Distributed system concepts
• Distributed system design goals
• Architectures
• Coordination in Distributed Systems:
• Logical Clocks
• Lamport’s Logical Clocks
• Vector Clocks
• Mutual Exclusion
• Election Algorithms
2

3. Coordination:
 Mutual Exclusion
 Election Algorithms
Reading Assignment Mutual Exclusion and Election
Algorithms: Text book 6.3 and 6.4
3

4. Mutual Exclusion
 A centralized algorithm
 Permission-based
 A distributed algorithm
 Ricart & Agrawala
 A token-ring algorithm
 A decentralized mutual exclusion
4

5. Overview of Mutual exclusion
Problem
A number of processes in a distributed system want exclusive access to some
resource.
Basic solutions
Permission-based: A process wanting to enter its critical section, or access a
resource, needs permission from other processes.
Token-based: A token is passed between processes. The one who has the
token may proceed in its critical section, or pass it on when not
interested.
5

6. Requirements
1. Correctness/Safety:
• At most one process holds the lock/enter C.S. at a time
2. Fairness:
• Any process that makes a request must be granted lock
• Implies that system must be deadlock-free
• Assumes that no process will hold onto a lock indefinitely
• Eventual fairness: Waiting process will not be excluded
forever
• Bounded fairness: Waiting process will get lock within
some bounded number of cycles (typically n)
6

7. Other Requirements
• Low message overhead
• No bottlenecks
• Tolerate out-of-order messages
• Allow processes to join protocol or to drop out
• Tolerate failed processes
• Tolerate dropped messages
7

8. Mutual Exclusion
A Centralized Algorithm (1)
@ Client  Acquire:
Send (Request, i) to coordinator
Wait for reply
@ Server:
while true:
m = Receive()
If m == (Request, i):
If Available():
Send (Grant) to i
8

9. Mutual Exclusion
A Centralized Algorithm (2)
@ Server:
while true:
m = Receive()
If m == (Request, i):
If Available():
Send (Grant) to I
else:
Add i to Q
9

10. Mutual Exclusion
A Centralized Algorithm (3)
@ Server:
while true:
m = Receive()
If m == (Request, i):
If Available():
Send (Grant) to I
else:
Add i to Q
If m == (Release)&&!empty(Q):
Remove ID j from Q
Send (Grant) to j
@ Client  Release:
Send (Release) to coordinator
10

11. Mutual Exclusion
A Centralized Algorithm (4)
• Correctness:
• Clearly safe
• Fairness depends on queuing policy.
• E.g., if always gave priority to lowest process ID, then
processes 1 & 2 lock out 3
• Performance
• "cycle" is a complete round of the protocol with one process i
entering its critical section and then exiting.
• 3 messages per cycle (1 request, 1 grant, 1 release)
• Lock server creates bottleneck
• Issues
• What happens when coordinator crashes?
• What happens when it reboots?
11

12. Permission-based, centralized
Coordinator
Queueis
empty
Simply use a coordinator
P0 P1 P2
Request OK
C
No reply
P0 P1
Request
P2
C
2
Release
OK
P0
P1
P2
C
(a) (b) (c)
(a) Process P1 asks the coordinator for permission to access a shared
resource. Permission is granted.
(b) Process P2 then asks permission to access the same resource. The
coordinator does not reply.
(c) When P1 releases the resource, it tells the coordinator, which then replies
to P2.
12

13. Ricart & Agrawala, Distributed
The same as Lamport except that acknowledgments are not sent
Return a response to a request only when:
The receiving process has no interest in the shared resource; or
The receiving process is waiting for the resource, but has lower priority
(known through comparison of timestamps).
In all other cases, reply is deferred, implying some more local administration.
13

14. A Distributed Algorithm 3
(Ricart & Agrawala)
• Also relies on Lamport totally ordered clocks.
• When node i wants to enter C.S., it sends time-
stamped request to all other nodes. These other
nodes reply (eventually). When i receives n-1
replies, then can enter C.S.
• Trick: Node j having earlier request doesn't reply
to i until after it has completed its C.S.
14

15. A Distributed Algorithm
Three different cases:
1.If the receiver is not accessing the resource and does not
want to access it, it sends back an OK message to the
sender.
2.If the receiver already has access to the resource, it simply
does not reply. Instead, it queues the request.
3.If the receiver wants to access the resource as well but has
not yet done so, it compares the timestamp of the incoming
message with the one contained in the message that it has
sent everyone. The lowest one wins.
15

16. A Distributed Algorithm
• Two processes (0 and 2) want to access a
shared resource at the same moment.
16

17. A Distributed Algorithm
• Process 0 has the lowest timestamp, so it wins.
17

18. A Distributed Algorithm (4)
• When process 0 is done, it sends an OK also, so
2 can now go ahead.
18

19. Example with three processes
0
1 2
8
8
8 12
12
12
0
1 2
OK OK
OK
Accesses
resource
0
1 2
OK
Accesses
resource
(a) (b) (c)
(a) Two processes want to access a shared resource at the same moment.
(b) P0 has the lowest timestamp, so it wins.
(c) When process P0 is done, it sends an OK also, so P2 can now go ahead.
Ricart & Agrawala, Distributed cont..
19

20. Performance
• Each cycle involves 2(n-1) messages
• n-1 requests by I
• n-1 replies to I
• Issues
• What if node fails?
• How is the performance compared to centralized?
20

21. Token ring algorithm
Essence
Organize processes in a logical ring, and let a token be passed between them.
The one that holds the token is allowed to enter the critical region (if it wants
to).
An overlay network constructed as a logical ring with a circulating token
0 1 2 3
4
5
6
7
T
oken
21

22. A Token Ring Algorithm
• Organize the processes involved into a logical ring
• One token at any time  passed from node to
node along ring
22

23. A Token Ring Algorithm
• Correctness:
• Clearly safe: Only one process can hold token
• Fairness:
• Will pass around ring at most once before getting
access.
• Performance:
• Each cycle requires between 1 - ∞ messages
• Latency of protocol between 0 & n-1
• Issues
• Lost token
23

24. Decentralized mutual exclusion
Principle
Assume every resource is replicated N times, with each replica having its own
coordinator ⇒ access requires a majority vote from m > N/2 coordinators. A
coordinator always responds immediately to a request.
Assumption
When a coordinator crashes, it will recover quickly, but will have forgotten about
permissions it had granted.
24

25. Decentralized mutual exclusion
25

26. Decentralized mutual exclusion
26

27. Mutual exclusion: comparison
27

28. Election Algorithms
 The bully algorithm
 The ring algorithm
28

29. Election algorithms
Principle
An algorithm requires that some process acts as a coordinator. The question is
how to select this special process dynamically.
Note
In many systems the coordinator is chosen by hand (e.g. file servers). This
leads to centralized solutions ⇒ single point of failure.
29

30. Election algorithms
Principle
An algorithm requires that some process acts as a coordinator. The question is
how to select this special process dynamically.
Note
In many systems the coordinator is chosen by hand (e.g. file servers). This
leads to centralized solutions ⇒ single point of failure.
Teasers
1
2
If a coordinator is chosen dynamically, to what extent can we speak about
a centralized or distributed solution?
Is a fully distributed solution, i.e. one without a coordinator, always more
robust than any centralized/coordinated solution?
30

31. Basic Assumptions: Bullying
All processes have unique id’s
All processes know id’s of all processes in the system (but not if they are
up or down)
Election means identifying the process with the highest id that is up
31

32. Election by bullying: The Bully Alg.
Principle
Consider N processes {P0 ,...,PN−1} and let id (Pk ) = k . When a process Pk
notices that the coordinator is no longer responding to requests, it initiates an
election:
1
2
3
Pk sends an ELECTION message to all processes with higher identifiers:
Pk+1,Pk+2,...,PN−1.
If no one responds, Pk wins the election and becomes coordinator.
If one of the higher-ups answers, it takes over and Pk ’s job is done.
32

33. The Bully Algorithm (1)
• The bully election algorithm. (a) Process 4 holds an
election. (b) Processes 5 and 6 respond, telling 4 to
stop. (c) Now 5 and 6 each hold an election.
33

34. The Bully Algorithm (2)
• The bully election algorithm. (d) Process 6 tells 5
to stop. (e) Process 6 wins and tells everyone.
34

35. Election by bullying
The bully election algorithm
Election
1
2
4
0
5
6
3
7
OK
1
2
4
0
5
6
3
7
Election
1
2
4
0
5
6
3
7
OK
1
2
4
0
5
6
3
7
Coordinator
1
2
4
0
5
6
3
7
35

36. Election in a ring: The ring algorithm
Principle
Process priority is obtained by organizing processes into a (logical) ring.
Process with the highest priority should be elected as coordinator.
Any process can start an election by sending an election message to its
successor. If a successor is down, the message is passed on to the next
successor.
If a message is passed on, the sender adds itself to the list. When it gets
back to the initiator, everyone had a chance to make its presence known.
The initiator sends a coordinator message around the ring containing a
list of all living processes. The one with the highest priority is elected as
coordinator.
36

37. Election in a ring
Election algorithm using a ring
1 2 3 4
5
6
7
0
[3]
[3,4]
[3,4,5]
[3,4,5,6]
[3,4,5,6,0]
[3,4,5,6,0,1] [3,4,5,6,0,1,2]
[6]
[6,0]
[6,0,1] [6,0,1,2] [6,0,1,2,3]
[6,0,1,2,3,4]
[6,0,1,2,3,4,5]
The solid line shows the election messages initiated by P6
The dashed one the messages by P3
37

38. Summary
 Mutual Exclusion
 A centralized algorithm
 Permission-based
 A distributed algorithm
 Ricart & Agrawala
 A token-ring algorithm
 A decentralized mutual exclusion
 Election Algorithms
 The bully Algorithm
 Ring Algorithm
Reading Assignment Mutual Exclusion and Election Algorithms
Text book 6.3 and 6.4
38