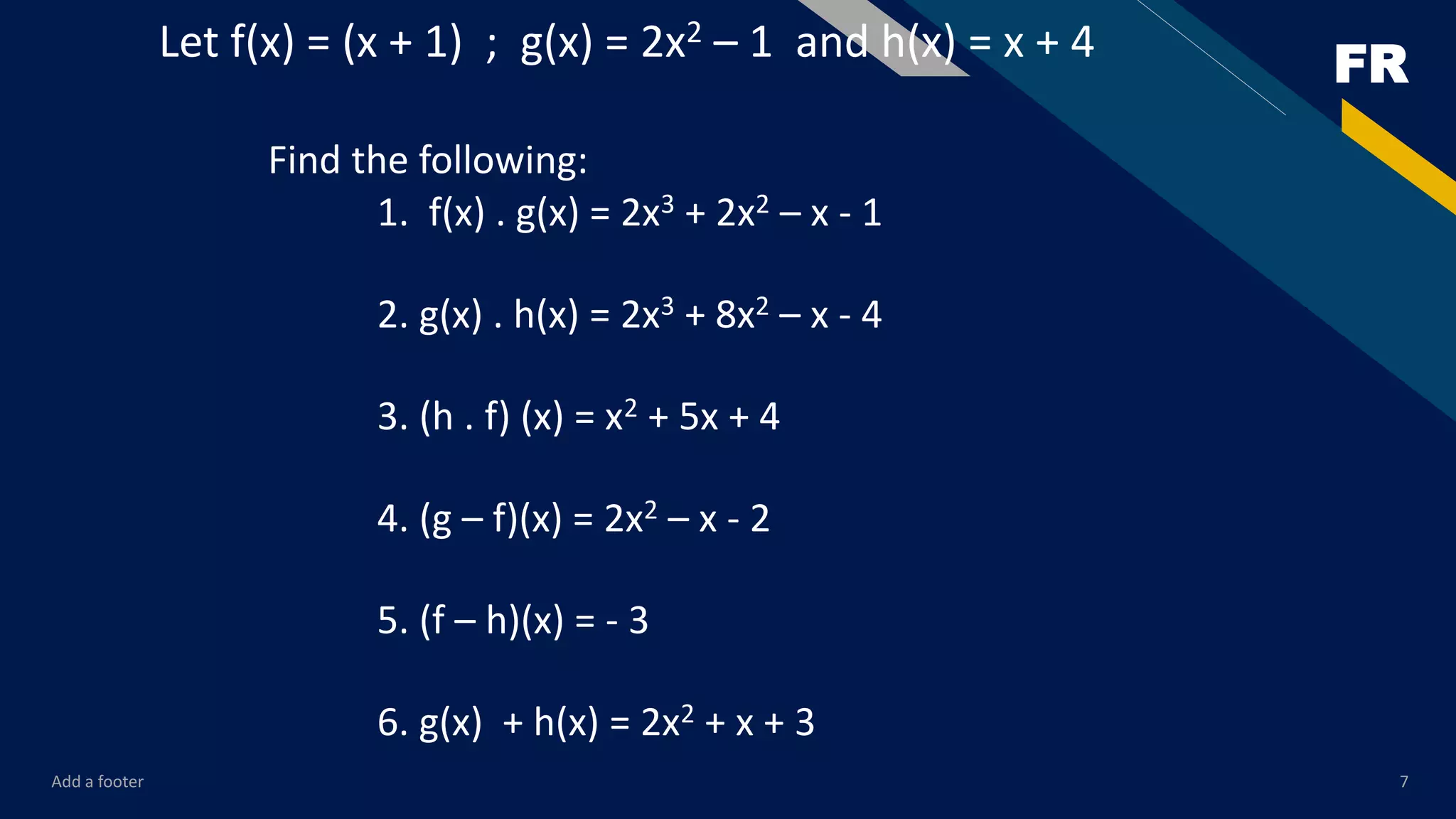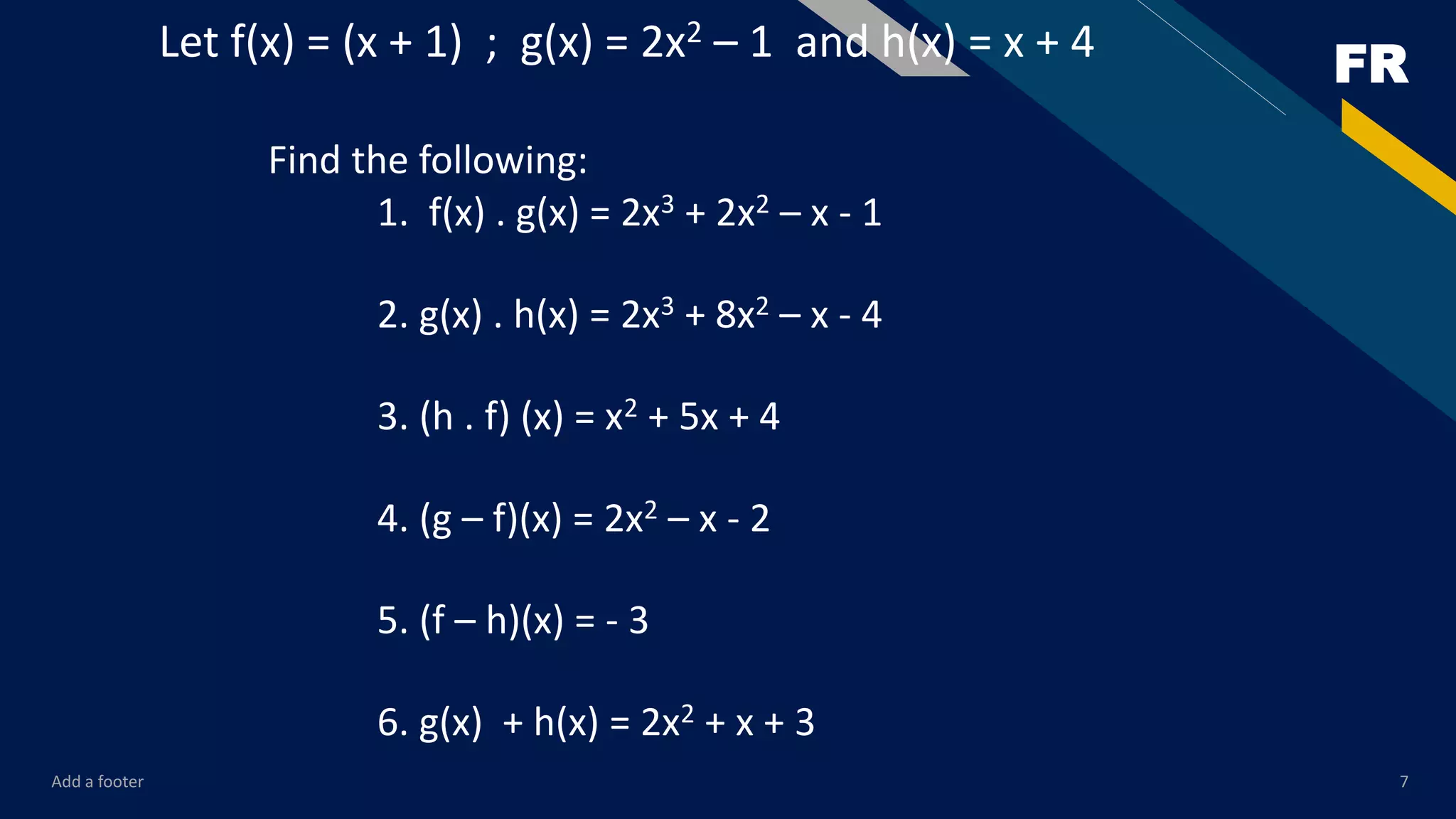
To multiply polynomial functions f and g: 1. Multiply the first term of f with each term of g to get partial products 2. Add the partial products For the given polynomials f(x) = 7x + 1, g(x) = 4x - 7, h(x) = 2x^2 - 3x + 5: (f·g)(x) = 28x^2 - 45x - 7 (h·g)(x) = 8x^3 - 26x^2 + 41x - 35 (f·h)(x) = 14x^3 - 19x^2 + 32x + 5

2. FR
Add a footer 2
Let’s remember
To multiply two polynomials functions f and g, follow these steps:
1. Multiply the first polynomial function by the first term of the
second polynomial function to obtain the first partial product.
2. Multiply the first polynomial function by the second term of
the second polynomial function to obtain the second partial product.
3. Repeat the preceding step as necessary.
4. Add the partial products.

3. FR
Add a footer 3
Let f(x) = 7x + 1 ; g(x) = (4x – 7) and h(x) = 2x2 – 3x + 5
Find the following the following:
1. (f . g)(x) =
2. (h . g)(x) =
3. (f . h)(x) =

4. FR
Add a footer 4
Let f(x) = 7x + 1 ; g(x) = (4x – 7) and h(x) = 2x2 – 3x + 5
1. (f . g)(x) means f(x) . g(x)
= (7x + 1)(4x – 7)
= 7x(4x – 7) + 1(4x – 7) - (Horizontal method)
= 28x2 – 49x + 4x – 7 - (Combine like terms)
= 28x2 – 45x – 7
Therefore, (f . g)(x) = 28x2 – 45x – 7

5. FR
Add a footer 5
Let f(x) = 7x + 1 ; g(x) = (4x – 7) and h(x) = 2x2 – 3x + 5
2. (h . g)(x) = h(x) . g(x)
= (2x2 – 3x + 5)(4x – 7)
= 2x2(4x – 7) – 3x (4x – 7) + 5 (4x – 7) – (Horizontal method
= 8x3 – 14x2 – 12x2 + 21x + 20x – 35 - (Combine like terms)
= 8x3 – 26x2 + 41x – 35
Therefore, (h . g)(x) is 8x3 – 26x2 + 41x – 35.

6. FR
Add a footer 6
Let f(x) = 7x + 1 ; g(x) = (4x – 7) and h(x) = 2x2 – 3x + 5
3. (f . h)(x) = f(x) . h(x)
= (7x + 1 )(2x2 – 3x + 5)
= 7x(2x2 – 3x + 5) + 1(2x2 – 3x + 5)
= 14x3 – 21x2 + 35x + 2x2 – 3x + 5 - (combine like terms)
= 14x3 – 19x2 + 32x + 5
Therefore, (f . h)(x) = 14x3 – 19x + 32x + 5

7. FR
Add a footer 7
Let f(x) = (x + 1) ; g(x) = 2x2 – 1 and h(x) = x + 4
Find the following:
1. f(x) . g(x) = 2x3 + 2x2 – x - 1
2. g(x) . h(x) = 2x3 + 8x2 – x - 4
3. (h . f) (x) = x2 + 5x + 4
4. (g – f)(x) = 2x2 – x - 2
5. (f – h)(x) = - 3
6. g(x) + h(x) = 2x2 + x + 3