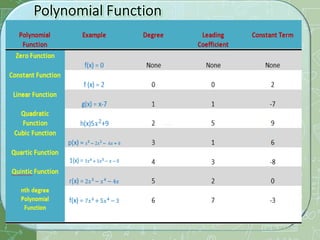
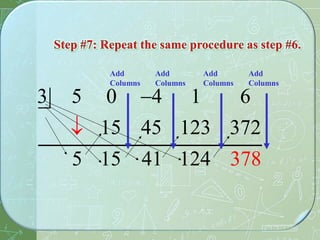
The document discusses polynomial functions. It defines polynomials as algebraic expressions consisting of terms in the form axn where a is a real number and n is a non-negative integer. The degree of a polynomial refers to the highest exponent of its terms. A polynomial function P(x) is written as P(x) = anxn + an-1xn-1 + ... + a2x2 + a1x + a0 where n is the degree. The document provides examples of finding the degree of polynomials and performing operations like addition and multiplication on polynomial functions. It also demonstrates using synthetic division to divide one polynomial by another.

1. Lesson 2-1:
General Form of a
Polynomial Function

2. Polynomial Function
 Polynomials – are defined as an algebraic expression
consisting of terms in the form 𝑎𝑥𝑛
where a is any real
number and n is a non-negative integer. Terms of
polynomials are separated by signs of operations.
 Degree of a Polynomial – the degree of a term in a
polynomial refers to the highest exponent of the literal
coefficient.
 Ex. 𝟓𝒙𝟑
+ 2x - 8
 the degree of the polynomial is 3

3. Polynomial Function - P(x)
 Is a function that can be written in the form
P(x) = 𝑎𝑛𝑥𝑛
+ 𝑎𝑛−1𝑥𝑛−1
+ …+ 𝑎2𝑥2
+ 𝑎1𝑥 + 𝑎0
 Where n is a nonnegative integer, the coefficients
𝑎0, 𝑎1 , 𝑎2 , …, 𝑎𝑛−2 , 𝑎𝑛−1 , 𝑎𝑛𝑑𝑎𝑛 are real numbers, and
𝑎𝑛 ≠ 0. The coefficient 𝑎𝑛 is called the leading
coefficient and the n is the degree of the polynomial.
 The Degree of a Polynomial refers to the highest
degree of the terms in a polynomial

4. Find the degree of the term and the degree of the
polynomial
a. 7𝑥4
b. 3𝑚𝑛4
b. c. 11𝑔2
+ 9𝑔 − 2 d. 4𝑏3
𝑐2
+9𝑏2
𝑐-b +12

6. Ex. 2.2
Perform the indicated operation : (𝟒𝒎𝟐 + 𝟕) + (𝟑𝒎𝟐 - 𝟏𝟏𝒎𝟒)
(𝟒𝒎𝟐
+ 𝟕) + (𝟑𝒎𝟐
- 𝟏𝟏𝒎𝟒
)
𝟒𝒎𝟐 + 𝟕+ 𝟑𝒎𝟐 - 𝟏𝟏𝒎𝟒
− 𝟏𝟏𝒎𝟒
+ 𝟕𝒎𝟐
+ 𝟕
In subtracting polynomials, also identify like terms.To
combine like terms, change the sign of the subtrahend and
proceed with the addition

7. Ex. 2.3
Perform the indicated operation : (5𝑎2 + 7 − 2𝑎) - (12-𝑎2)
(𝟓𝒂𝟐
+ 𝟏 − 𝟐𝒂) - (12-𝒂𝟐
)
In subtracting polynomials, also identify like terms.To
combine like terms, change the sign of the subtrahend and
proceed with the addition
(𝟓𝒂𝟐
+ 𝟏 − 𝟐𝒂) + (-12+𝒂𝟐
)
𝟓𝒂𝟐
+ 𝟏 − 𝟐𝒂 – 12 + 𝒂𝟐
𝟔𝒂𝟐
− 𝟐𝒂 – 11

8. Ex. 2.3
Perform the indicated operation :
a. 3x(2𝑥2-7x+10)
b. (3b - 4)(8b + 5)
c. (2y +13)(5𝑦2
+ 3y -2)

9. Consider the cubic function f(x) = 2𝑥3
− 5𝑥2
+ 12x − 6
Evaluate the function f at each given value.
a. x = 0
b. x = -1
c. x= a
d. x= -a

10. For any two polynomial functions f(x) and g (x), the following
operations are defined as follows:
 (f ± g)(x) = f(x) ± g(x)
Fundamental Operations on Polynomial Functions
 (fg)(x) = f(x) • g(x)

𝒇
𝒈
𝒙 =
𝒇(𝒙)
𝒈 (𝒙)
, 𝒘𝒉𝒆𝒓𝒆 𝒈 𝒙 ≠ 𝟎

11. Example 2.7
Identify which of the following mathematical expressions are
polynomial functions.
1. 𝑓(𝑥) = (𝑥 + 3)2
2. 𝑔 𝑥 = −2𝑥−2
+ 𝑥 − 11
3. ℎ 𝑥 = 1 − 𝑥3
4. 𝑓 𝑥 = 𝑥3
- 2𝑥 + 9
5. 𝑔 𝑥 = 𝑥
1
3 + 7𝑥 − 2
6. ℎ 𝑥 = −7𝑥 + 𝑥𝑛- 4

12. Example 2.9
Given p(x) = 𝟑𝒙𝟐 + 𝟓𝒙 − 𝟏𝟎, find:
a. p(1) b. p(-2)

13. Example 2.9
Given p(x) = 𝟑𝒙𝟐 + 𝟓𝒙 − 𝟏𝟎, find:
c. p(5) d. p(x+3)

14. Example 5
Consider the given polynomial functions.
f(x) = 𝟒𝒙𝟐
− 𝟐𝒙 + 𝟏
g(x) = 𝟑𝒙 − 𝟐
a. (f +g)(x) b. (f -g)(x) c. h(x) + 2g(x) – f(x)
h(x) = 𝟓𝒙𝟑
− 𝟑𝒙𝟐
+ 𝟐𝒙 + 𝟓 𝟓𝒙𝟑

15. Example 5
Consider the given polynomial functions.
f(x) = 𝟒𝒙𝟐
− 𝟐𝒙 + 𝟏
g(x) = 𝟑𝒙 − 𝟐
a. (f +g)(x) b. (f -g)(x) c. h(x) + 2g(x) – f(x)
h(x) = 𝟓𝒙𝟑
− 𝟑𝒙𝟐
+ 𝟐𝒙 + 𝟓

16. Example 5
Consider the given polynomial functions.
f(x) = 𝟒𝒙𝟐
− 𝟐𝒙 + 𝟏
g(x) = 𝟑𝒙 − 𝟐
a. (f +g)(x) b. (f -g)(x) c. h(x) + 2g(x) – f(x)
h(x) = 𝟓𝒙𝟑
− 𝟑𝒙𝟐
+ 𝟐𝒙 + 𝟓

17. Example 5
Consider the given polynomial functions.
a. (f +g)(x) b. (f -g)(x) c. h(x) + 2g(x) – f(x)

18. 5x4
 4x2
 x  6(x 3)
In order to use synthetic division these
two things must happen:
There must be a
coefficient for
every possible
power of the
variable.
The divisor must
have a leading
coefficient of 1.
#1 #2

19. 5x4
 0x3
 4x2
 x  6
Since the numerator does not contain all the powers of x,
you must include a 0 for the x3
.

20. Step #2: Write the constant a of the divisor
x- a to the left and write down the
coefficients.
5x4
0x3
4x2
x 6
    
3 5 0 4 1 6

21. 3 5 0 4 1 6

5
Step #4: Multiply the first coefficient by r (3*5).
5
3 5 0 4 1 6
 15

22. Add the
column
3 5 0 4 1 6
 15
5 15

23. 3 5 0 4 1 6
 15 45
Add
5 15 41
Multiply the diagonals, add the columns.

24.  15 45 123 372
5 15 41 124 378
3 5 0 4 1 6
Add
Columns
Add
Columns
Add
Columns
Add
Columns

25. 5x3
15x2
 41x 124 
378
x  3
Remember to place the
remainder over the divisor.

26. 1) (t3
 6t2
1 ) (t  2)