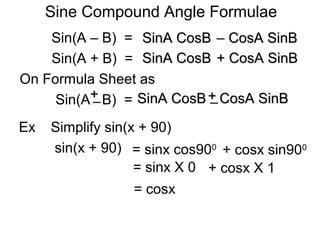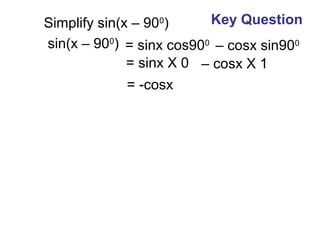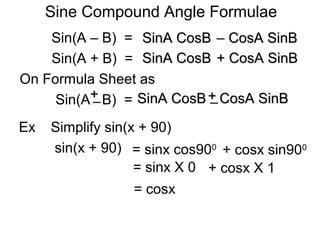
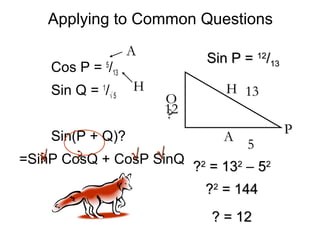
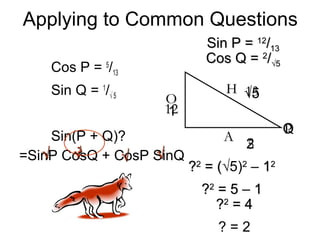
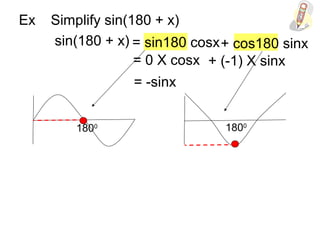
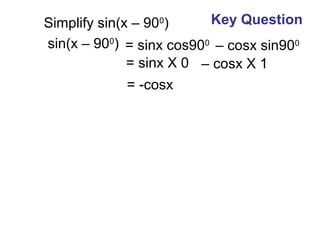
1) The document discusses sine compound angle formulae and provides examples of applying the formulae to simplify expressions like sin(x + 90) and sin(x - 90). 2) It also works through an example problem of finding sin(P + Q) given values for sinP, cosP, sinQ, and cosQ. 3) The key question is about simplifying sin(x - 90), which the document shows equals -cosx using the compound angle formula sin(A - B) = sinAcosB - cosAsinB.

1. Block 2
More Compound Angle
Formulae

2. What is to be learned?
• Rules for sin

3. Sine Compound Angle Formulae
Sin(A – B) =
Sin(A + B) =
On Formula Sheet as
Sin(A B) =
SinA CosBSinA CosB – CosA SinBCosA SinB
SinA CosBSinA CosB + CosA SinB+ CosA SinB
SinA CosBSinA CosB CosA SinBCosA SinB++
– ++–
Ex Simplify sin(x + 90)
sin(x + 90) = sinx cos900
= sinx X 0 + cosx X 1
= cosx
+ cosx sin900

4. Applying to Common Questions
Cos P = 5
/13
Sin Q = 1
/√ 5
Sin(P + Q)?
=SinP CosQ + CosP SinQ
PP
OO
HH
AA
AA
HH
55
1313
??
??22
= 13= 1322
– 5522
??22
= 144= 144
? = 12? = 12
1212
Sin P =Sin P = 1212
//1313
√√ √√?? ??√√

5. Cos P = 5
/13
Sin Q = 1
/√ 5
Sin(P + Q)?
=SinP CosQ + CosP SinQ
PP
OO
HH
AA
55
1313
??22
= (= (√5)22
– 1122
??22
= 5= 5 – 11
??22
= 4= 4
1212
Cos Q =Cos Q = 22
//√5√5
√√ √√√√
Q
1
√5
? = 2
2
√√
Sin P =Sin P = 1212
//1313
??
Applying to Common Questions

6. Cos P = 5
/13
Sin Q = 1
/√ 5
Sin(P + Q)?
=SinP CosQ + CosP SinQ
= 12
/13 X 2
/√5 + 5
/13 X 1
/√5
= 24 + 5
Cos Q =Cos Q = 22
//√5√5
√√ √√√√√√
Sin P =Sin P = 1212
//1313
13√5 13√5
= 29
13√5
Applying to Common Questions

7. Sine Compound Angle Formulae
Sin(A - B) =
Sin(A + B) =
On Formula Sheet as
Sin(A B) =
SinA CosBSinA CosB – CosA SinBCosA SinB
SinA CosBSinA CosB + CosA SinB+ CosA SinB
SinA CosBSinA CosB CosA SinBCosA SinB++
– ++–

8. Ex Simplify sin(180 + x)
sin(180 + x) = sin180 cosx+ cos180 sinx
= 0 X cosx + (-1) X sinx
= -sinx
1800 1800

9. Simplify sin(x – 900
)
sin(x – 900
) = sinx cos900
= sinx X 0 – cosx X 1
= -cosx
– cosx sin900
Key Question

10. Simplify sin(x – 900
)
sin(x – 900
) = sinx cos900
= sinx X 0 – cosx X 1
= -cosx
– cosx sin900
Key Question