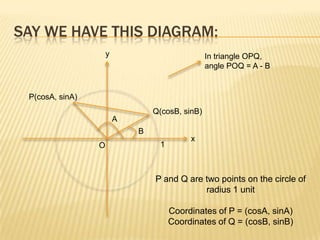
1) The document demonstrates how to prove trigonometric identities using sum and difference formulas by relating trigonometric functions of two angles (A and B) to the functions of their sum or difference. 2) It derives the identities cos(A+B)=cosAcosB - sinAsinB and sin(A+B)=sinAcosB + cosAsinB through using distance and angle formulas in a triangle. 3) Further identities like tan(A+B), tan(A-B) are derived by substituting the expressions for sin(A+B) and cos(A+B) in the definition of tangent.

1. Proving trigonometrical identitiesusing sum and difference of two anglesVania LundinaGrade 10

2. Basic knowledge

3. Say we have this diagram:yIn triangle OPQ, angle POQ = A - BP(cosA, sinA)Q(cosB, sinB)ABx1OP and Q are two points on the circle of radius 1 unitCoordinates of P = (cosA, sinA)Coordinates of Q = (cosB, sinB)

4. Now we can form an equation using:The distance formula PQ2 = (cosA-cosB)2 + (sinA-sinB)2 = cos2A – 2cosAcosB + cos2B + sin2A – 2sinAsinB + sinB2= 2 – 2(cosAcosB + sinAsinB)The cosine formula from triangle OPQPQ2 = 12 + 12 – 2(1)(1)cos(A-B) = 2 – 2cos(A-B)

5. From the two equations, we get:2 – 2(cosAcosB + sinAsinB) = 2 – 2cos(A-B)We can cross out the “ 2 – 2 “ from the equation;2 – 2(cosAcosB + sinAsinB) = 2 – 2cos(A-B)cos(A-B) = cosAcosB + sinAsinB

6. Replace B with (-B) into;cos[A-(-B) = cosAcos(-B) + sinAsin(-B)since cos(-B) = cosB and sin(-B) = -sinB, the equation can be simplified into;cos(A+B) = cosAcosB - sinAsinB

7. Since sin ϑ = COS (900 – ϑ)sin(A+B) = cos[900 – (A+B)] = cos[(900 – a) – B] = cos(900 – A) cosB + sin(900 – A)sinBSo, sin(A+B) = sinAcosA + cosAsinB

8. Replace B with (-B) from the previous equation, we have;Sin(A-B) = sinAcos(-B) + cosAsin(-B)Sin(A-B) = sinAcosB-cosAsinB

9. tan(A+B) = sin(A+B)cos(A+B) = sinAcosB + cosAsinBcosAcosB – sinAsinB = tanA + tanB 1 – tanAtanB

10. Replace b with (-B), we have;tan(A-B) = tan A + tan (-B) 1 – tan A tan(-B)tan(A-B) = tanA – tanB 1 + tanAtanB

11. EXAmples

12. Simplify the equation sin 370cos 410 + cos 370 sin 410;sinAcosB + cosAsinB = sin(A+B)sin37cos 41 + cos37sin41 = sin(37 + 41) = sin 780

13. Simplify 1 – tan150 1 + tan150tan A – tan B = tan (A-B)1 + tanAtanBtan 45 – tan 15 = tan(45-15) 1 + tan 45 tan 151 – tan 15 = tan 3001 + tan 15