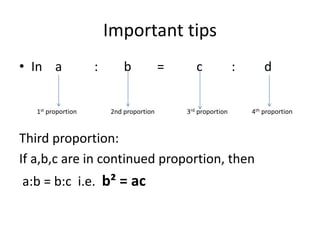
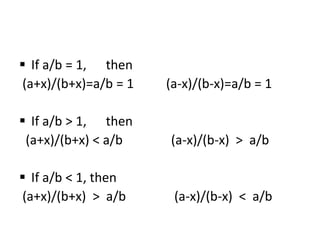This document discusses ratios and proportions. It provides examples of using ratios to solve problems involving splitting amounts according to given ratios. It also discusses properties of ratios, such as comparing two ratios and how ratios behave when numbers in the ratios increase or decrease. The document concludes with examples of using ratios in problems involving three and four terms.

1. Ratio and Proportion
By
Vishwanath K

2. Some important tips
 First part = a1/(a1+a2) * A
 Second part = a2/(a1 + a2) * A
Problems:
1) Two numbers are in the ratio 8:9, If sum of the numbers is 119,find the numbers.
2) Dividing Rs 3,200 among P,Q,R in the ratio 5:2:9 , Find the amount received by Q.

3.  In ratios a:b and c:d
a:b > c:d if ad>bc i.e. a/b>c/d
a:b < c:d if ad<bc i.e. a/b<c/d
• Problem:
1) Compare 5:7 and 2:3

4.  If a/b = 1, then
(a+x)/(b+x)=a/b = 1 (a-x)/(b-x)=a/b = 1
 If a/b > 1, then
(a+x)/(b+x) < a/b (a-x)/(b-x) > a/b
 If a/b < 1, then
(a+x)/(b+x) > a/b (a-x)/(b-x) < a/b

5. • Problems :
• Consider the ratio 7/5 and explain the above
properties.
• Consider the ratio 4/9 and explain the above
properties

6. Proportion
a,b,c,d are in proportion if
Product of means = Product of extremes
Consider a:b = c:d
Means = b and c Extremes = a and d
The ratios are in proportion only if
ad = bc

7. When a:b = c:d or a/b = c/d
1) b/a = c/d
2) a/c = b/d
3) c/a = d/b
4) (a+b)/b = (c+d)/d
5) (a-b)/b = (c-d)/d
6) (a+b) / (a-b) = (c+d) / (c-d)
7) a/(a-b) = c/ (c-d)

8. Important tips
• In a : b = c : d
1st proportion 2nd proportion 3rd proportion 4th proportion
Third proportion:
If a,b,c are in continued proportion, then
a:b = b:c i.e. b² = ac

9. • Problems.
• Find the mean proportional between 9 and
16.
• If 3,x,27 are in continued proportion, Find x

10. Three terms
Given a:b = x:y and b:c = p:q
a : b = x : y
b : c = p : q
a : b : c = xp : py : yq
a:c = xp : yq
Problem: If incomes of Ram and Shyam are in the ratio 3:5 and that of Shyam and
Mohan are in the ratio of 7:4, find the ratios of incomes of Ram, Shyam and
Mohan.

11. Four terms
Given a:b = x:y, b:c = p:q, c:d = m:n
a : b = x : y
b : c = p : q
c : d = m : n
a:b:c:d = xpm : ypm : yqm : yqn
a : d = xpm : yqn
Problem: Find B’s share in Rs 6,300 if A:B = 2:3, B:C = 4:5 and C:D = 3:7.