Mom slideshow

METHOD OF MOMENT
COMPUTATIONAL TECHNIQUE
Dr. Ashutosh Kedar

Contents
 PART I
 Brief history
 Theory
 PART II
 APPLICATION:
 WIRE TYPE ANTENNAS
 PATCH ANTENNA
 BAND PASS FILTER
Dr. Ashutosh Kedar

Origin
 Most of the solutions to linear functional equations can be
interpreted in terms of projections onto sub spaces of
functional spaces. For computational reasons, these sub-
spaces must be finite-dimensional, For theoretical work, they
may be infinite dimensional. The idea of transforming linear
functional equation to a matrix equation is relatively old.
Galerkin (1915), Russian mechanical engineer developed his
method, carrying its name in 1915.
 Preference to analytical methods because of lack of high speed
computers
 First large scale effort made during World War II at MIT
Radiation lab.
 Schwinger et.al applied Variational Technique to
microwave problems
 Rumsay formalized some of the concepts into a more
compact notation in his “Reaction Concept”.
 1960s – researchers started solving EM field equations
using numerical methods
 Mei and van Bladel used a sub-sectional and point
matching method to compute scattering from
rectangular apertures
 Accuracy obtained was impressive
Dr. Ashutosh Kedar

References:
1. Origin and development of the Method of Moments for Field Computation-
Roger Harrington, IEEE Antennas and Propagation Society magazine, June
1990
2. Numerical Techniques in Electromagnetics, Matthew N. O. Sadiku, CRC
Press.
3. Field Computation by Moment Methods, R. F. Harrington.
4. Generalized Moment methods in Electromagnetics, J.J.H. Wang, John Wiley &
Sons.
 Earlier in Russian books, method of moments had been proposed
(Ref: L.V. Kantorovich and V.L. Krylov, Approximate Methods of Higher Analysis)
 The idea was extended by R.F. Harrington in solving EM field
equations using Method of Moments (1967)
 Earlier expansion and testing functions were chosen as same in
Galerkin’s and Rayleigh Ritz’s variational techniques but Harrington
in his method of moments shown that they can be chosen different
for computational conveniences still achieving the solution
stationary in form.
 The method owes its name to the process of taking moments by
multiplying with appropriate weighing functions and integrating
Dr. Ashutosh Kedar

• Most of the EM problems can be expressed under the form of a linear
functional equation . One generally classifies EM problems in two
categories: -deterministic and eigen value problems.
• Deterministic:-linear functional equation enables one to determine
the electromagnetic quantity directly
• Eigen-value:-parameters for which non-trivial solutions exist are
found first. Then the corresponding solutions called eigen solutions
are determined.
• MOM can handle both the kinds of problem. Most EM problems can be
stated as an inhomogeneous eqn.
• L : differential, integral or integro-differential operator
• g: known excitation or source function
• : unknown function to be determined
Procedure involves four steps:-
1. Derivation of the appropriate integral equation (IE),
2. Conversion (discretization) of the IE into a matrix equation using
basis (or expansion) functions and weightings (testing) functions,
3. Evaluation of the matrix elements, and
4. Solving the matrix equation and obtaining the parameters of
interest.
)1(gL 
Dr. Ashutosh Kedar

Fredholm IE of 1st, 2nd and 3rd kinds
)7()(),()()()(
)6()(),()()(
)5()(),()(
 
 
 
x
a
x
a
x
a
dtttxKxxaxf
dtttxKxxf
dtttxKxf


 is an scalar (or possibly complex) parameter;  is an unknown function;
K(x,t), f(x) , a and b are known; K(x,t) is known as kernel of the IE.
Volterra IE of 1st, 2nd and 3rd kinds
)4()(),()()()(
)3()(),()()(
)2()(),()(
 
 
 
b
a
b
a
b
a
dtttxKxxaxf
dtttxKxxf
dtttxKxf


Integral Equation (IE )
1. An IE is any equation involving unknown function, , under the
integral sign. Few examples are Fourier, Laplace an Hankel
transforms.
2. IEs can be classified under two categories:- (1) Fredholm equations
and (2) Volterra equations, of 1st, 2nd and 3rd kinds respectively.
Dr. Ashutosh Kedar

Consider the deterministic equation
Lf=g (1)
Let f is represented by a set of functions {f1,f2,f3,….} in the domain of L as a linear
combination
(2)
Where aj are scalars to be determined; fj are called expansion functions or basis
functions.
For approximate solutions (2) is a finite summation; for exact solution it is usually an
infinite summation. Substitute (2) into (1) and using linearity of L, we have
(3)
where the equality is usually approximate. Now defining a set of testing functions or
weighting functions {w1, w2, w3,….}in the range of L.
Take the inner product (usually an integration) of (3) with each wi, and use the linearity
of the inner product to obtain
(4)

j
jj ff 
gLf jj 
  gwLfw ijij ,,
i=1,2,3,….This set of equations can be written in matrix form as
(5)
where [l] is the matrix
(6)
  gl 
   ii Lfwl ,
Dr. Ashutosh Kedar
Method of
Moments

and  and g are column vectors
(7)
(8)
and if [l] is singular, its inverse exists, and  i given as
(9)
The solution of f is then given by (2). For concise notation, define the row vector
of functions
(10)
Write (2) as and substitute from (9). The results is
(11)
 This solution may be either approximate or exact, depending upon the choice
of expansion functions and testing functions.
 
 gwg i
j
,
 
  gl 1

 jff 
~
ff
~

  1~ 
 lff
Dr. Ashutosh Kedar

Dr. Ashutosh Kedar
The method of moments may also be applied to the eigen value equations
(not taken up here will be taken in last if time permits).
Ref:- R.F. Harrington, Field Computations by Moment methods, NY, The
MacMillan, 1968.
The name method of moments derives from the original terminology that
is the nth moment of f. When xn is replaced by an arbitrary wn, we
continue to call the integral a moment of f. the name method of weighted
residuals derives from the following interpretation. If (3) represents an
approximate equality, then the difference between the exact and approximate
Lf s is
(12)
which is called residual, r and the inner products are called weighted
residuals. Now (4) is obtained by setting all weighted residuals equal to zero.
 dxxfxn
)(
 
j
jj rLfg 
rwi ,

1. Eigenfunction method
The eigenfunction method is the special case for which the expansion
functions are taken to be eigen functions of L, and the testing functions,
eigen functions of the adjoint operator, La. Its difficult to find these eigen
functions, but once known the solution of Lf=g is simple.
In this case, the matrix [l] of (5) is diagonal, with elements equal to the
eigen values, i , when the eigen functions are normalized or
bioorthogonalized. The inverse [l]-1 then has diagonal elements and the
moment solution (11) reduces to eigenfunctions solutions.
2. Galerkin’s method
When the domains of L and La are the same, we can chose wi = fi, and
the specialization is known as Galerkin’s method. When L is self-adjoint,
this has advantage of making [l] a symmetric matrix. Since the solution of
symmetric matrices is easy compared to non-symmetric, particularly for
eigen value problems, this can be a theoretical advantage. However, for
computations, the evaluation of the elements of [l] may be difficult when
Galerkin’s method is used and this outweighs the advantage of keeping [l]
symmetric.
1
i
Dr. Ashutosh Kedar
Specializations
of the Method
of Moments

3. Point Matching or Collocation method
The simplest specialization of MOM. This basically involves satisfying the
approximate representation (3) at discrete points in the region of interest.
In terms of MOM, this is formally equivalent to choosing the testing
functions to be Dirac delta functions. The integration represented by inner
products now become trivial, which is the major advantage of this method.
This solution is sometimes sensitive to the points at which equation is
matched, which is major disadvantage of the method.
4. Least squares Method
Another possibility is that of minimizing the length or norm of the residual,
given by (12). If the usual inner product is used, the procedure is called a
least squares method. It is evident from (12) that minimization of r is
equivalent to finding the shortest distance from g to the subspace generated
by the Lfj, j=1,2,3…. Hence, by the projection theorem, the least norm is
obtained by taking the wi=Lfi in the method of moments.
Dr. Ashutosh Kedar

Part II:
Application:
1. Wire Type
Antennas
The objective: to cast an solution, for the unknown current density,
which is induced on the surface of the radiation scatterer, in the form of
Integral Equation (IE) where the unknown induced current density is a
part of integrand.
- The integral equation is then solved using MOM
- Start with electrostatic problem followed by time harmonic fields.
Electrostatic Charge Distribution: -
From statics  A linear electric charge distribution (r’) creates an
electric potential, V(r)
(1)
where r’(x’, y’, z’) is source and r(x,y,z) is observation point, dl’ is path of
integration and R is distance of any one point on the source from
observation point
(2)
ld
R
r
rV
ech
source


 
)arg(
0
)(
4
1
)(


222
)()()(),( zzyyxxrrrrR 

(1) may be used to calculate the potential that are due to any known line
charge density.
difficult for complex geometries, unknown line charge density-use of IE-
MOM technique for solving.
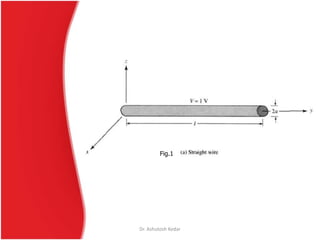
(A). Finite Straight Wire
The wire is of length l, and cross-sectional area a and is assumed to have
normalized constant electric potential of 1V. (1) is valid everywhere
including surface of the wire. Thus choosing the observation along the
wire axis (x=z=0) and representing the charge density of the wire as
(2)
where
(2a)
The observation point is chosen along the wire axis and the charge
density is expressed along the surface of wire so as to avoid R(y, y’)=0,
which would introduce singularity in integrand of (2).
lyyd
yyR
yl



  0;
),(
)(
4
1
1
0
0


22
222
0
)(
])[()(),(),(
ayy
zxyyrrRyyR zx

 
Dr. Ashutosh Kedar

Eq (2) is an IE that can be used to find the charge density (y’) based on
the the 1-V potential.
- The solution may be reached numerically by reducing (2) to a series of
linear algebraic equations that may be solved by conventional matrix
equation techniques.
- To facilitate this we approximate the unknown charge distribution (y’) by
an expansion of N known terms with constant, but unknown coefficients,
i.e.,
(3)
(4)
Since (4) is a non-singular integral, its summation and integration can be
interchanged
(4a)
   ygayp
N
n
nn
 1
ydyga
yyR
N
n
nn
l








  10
0 )(
),(
1
4)2( 
 




N
n
l
n
n yd
ayy
yg
a
1 0
220
)(
)(
4
Dr. Ashutosh Kedar

The wire is now divided into N uniform segments, each of length,
=l /N, as shown below.
gn(y’) should be chosen so as to correctly describe the unknown
quantity and also minimizing the computations. They are often
referred to as the basis or expansion functions.
 




N
n
l
n
n yd
ayy
yg
a
1 0
220
)(
)(
4
Dr. Ashutosh Kedar

Basis Functions chosen here are sub-domain piece-wise constant (or
pulse) function. These are having constant value over one segment and
zero elsewhere. (many other are available in literature)
(5)
Replacing y by a fixed point as ym, results in an integrand that is a solely a
function of y’, so that integral may be evaluated. Now (4) results into one
equation with N unknowns an,
(6)
 In order to obtain solution to these N amplitude constants, N linearly
independent equations are necessarily needed.






















l
N m
N
N
n
n m
n
n
mm
yd
yyR
yg
ayd
yyR
yg
a
yd
yyR
yg
ayd
yyR
yg
a
)1()1(
2
2
2
0
1
10
),(
)(
.....
),(
)(
....
......
),(
)(
),(
)(
4
Dr. Ashutosh Kedar

These equations may be produced by choosing N observation points,
ym, each at the centre of each  line element, as shown in figure 1b.
This results in one equation of the form (6) at each observation point.
(6a)
(7) Can be written in matrix form
(7)
where each Zmn is of the form
(7a)
Unknown charge distribution coeff.
(7b)
(7c)
Dr. Ashutosh Kedar

Solving for I, we get
(8)
can be solved by matrix inverse or equation solving routines using
computer resources.
One closed form representation of (7a) is also available
(9a)
(9b)
(9c)
(9d)
(9e)
lm is the distance between the mth matching point and the centre of the
nth source point.
 Accuracy depends on the number of basis functions (N).
       mmnnn VZaI
1

Dr. Ashutosh Kedar

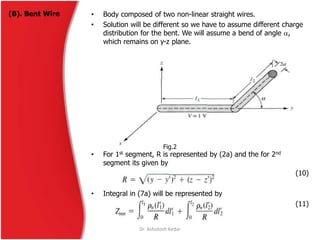
(B). Bent Wire • Body composed of two non-linear straight wires.
• Solution will be different so we have to assume different charge
distribution for the bent. We will assume a bend of angle ,
which remains on y-z plane.
• For 1st segment, R is represented by (2a) and the for 2nd
segment its given by
(10)
• Integral in (7a) will be represented by
(11)
Fig.2
Dr. Ashutosh Kedar

Integral
Equation
(review of what
we have studied
till now)
• Eq. (2) was an integral equation, which can be solved for charge
distribution.
• To solve numerically, unknown charge distribution (y’) is
represented by unknown terms (basis functions), while an
represents constant but unknown coefficients. Basis functions are
chosen to accurately represent the unknown charge distribution.
• Eq. (2) is valid everywhere on the wire. By enforcing (2) at N
discrete but different points on the wire, (2) is reduced to N
linearly independent algebraic equations, given by (6a).
• This set is generalized by (7)-(7c), then solved for unknown
using matrix inversion techniques. Since the system of n linear
equations each with N unknowns, as given by (6a)-(8), was
derived by applying the boundary condition (const 1-V potential)
at n discrete points on the wire, the technique is referred to as
the Point –Matching (or Collocation) Method.
Dr. Ashutosh Kedar

• For time-harmonic fields, two of the most popular integral
equations are the Electric Field Integral Equations (EFIE) and
Magnetic Field Integral Equations (MFIE).
• EFIE:- enforces the boundary condition on the tangential
components of electric field
– Valid for both closed and open surfaces
• MFIE:- enforces the boundary condition on the tangential
components of magnetic
field
– Valid for both closed surfaces
• These integral equations can be used to solve both radiation
and scattering problems.
• For radiation problems, especially wire antennas two popular IEs
are Pocklington IE and Hallén IEs.
Dr. Ashutosh Kedar

Finite
Diameter
Wire
• Pocklington integro-differential equation (PIE) and Hallén’s
integral equation (HIE) can be used most conveniently to find
the current distribution on conducting wires.
• HIE is usually restricted to the use of a delta-gap voltage source
model at feed of a wire antenna. It requires inversion of an N+1
order matrix (where N is no. of divisions of wire)
• PIE is more general and applicable to many types of feed sources
(through alteration in of its excitation function or excitation matrix)
including a magnetic frill. It requires inversion of N order matrix.
• For thin wires, current distribution is usually assumed to be of
sinusoidal form. For finite diameter wire, (usually diameter d
>0.05) In this sinusoidal approximation is not accurate and hence
IE needed to solved to have correct picture.
Dr. Ashutosh Kedar

Pocklington
Integral
Equation
• Valid for scatterer as well as an antenna
• Assume an incident wave impinges on the surface of a conducting
wire, as shown, and is referred as incident electric field Ei(r). (When
the wire is an antenna, incident field is produced by the field at the
gap (will be discussed later in Hallen IE)).
• Part of the incident field impinges on wire and indices an surface
current density Js (A/m). The induced current density re-radiates
and produces an electric field that is referred to as scattered electric
field Es(r).
• Therefore at any point in space the total Electric field Ei(r)is sum of
the incident and the scattered fields.
(12)
• When the observation point is moved on the surface of the wire
(r=rs) and the wire is perfectly conducting, total tangential electric
field vanishes. In cylindrical coordinates, the electric field radiated by
the dipole has a radial component (E) and a tangential component
(Ez). Therefore on the surface of wire (12) reduces to
(13)
(13a)
Dr. Ashutosh Kedar

• In general, scattered electric field generated by induced surface
current density Js is given by
(14)
• However for observations at the wire surface only z-component
is needed , hence,
(15)
• Neglecting edge effects we can write
(16)
If the wire is very thin, the current density Jz is not a function of the
azimuthal angle,  and we can write it as
(17)
where Iz(z’) is assumed to be an equivalent filament line-source
current located a radial distance =a from the z-axis, as shown in
next figure. Thus (16) reduces to
Dr. Ashutosh Kedar

(18)
(18a)
where  is the radial distance to the observation
point and a is the radius
Fig.3
Dr. Ashutosh Kedar

The observations are not a function of  because of symmetry. Let us
then chose =0 for simplicity. For observations on the surface =a of
the scatterer (18) and (18a) reduces to
(19)
(19a)
(19b)
The z-comp of the scattered electric field
(20)
Using (13a) reduces to
(21)
Dr. Ashutosh Kedar

(21) can be re-written as
(21a)
Interchanging integration with differentiation
(22)
where G(z,z’) is given by (19a).
Eq. (22) is called as Pocklington’s Integral Equation. It can be used to
determine the equivalent filamentary line-source current of the wire, and
thus current density on the wire, by knowing the incident field on the
surface of the wire.
If wire is very thin (a<<)
(23)
(22) In more convenient form
(24)
Where for observations along the centre (=0)
(24a)
Dr. Ashutosh Kedar

• In Eq. (22) and (24)
• Iz(z’) represents filamentary line source
current located on the surface of the wire
(see Fig.3b) and its obtained by knowing
the incident electric field on the surface of
the wire.
• Solution can be had using point matching
technique using matching points at the
interior of the wire, esp. along the axis
(see Fig.3a).
• By reciprocity, the configuration of Fig. 4a
is analogous to Fig. 4b where equivalent
filamentary line-source current is assumed
along the centre axis of the wire and
matching points are selected on the
surface of the wire.Fig.4
Dr. Ashutosh Kedar

• Referring to Fig. 3a, let us assume that the length of the cylinder is
much larger than its radius (l >> a) and its radius , a<<, so that
effects of the end faces of the cylinder can be neglected. Therefore
the boundary conditions for a wire with infinite conductivity are those
of vanishing total tangential E fields on the surface of the cylinder and
vanishing currents at the ends of the cylinder [ Iz (z’=±l /2)=0].
• Since only an electric current density flows on the cylinder and it is
directed along the z-axis (J=âz Jz), then A=âz Az (z’), which for smaller
radii is assumed to be a function of z’.
(25)
• Applying the boundary condition (vanishing tang. Elect. field)
(25a)
• Solution for (25a) assuming symmetry of current distribution
(26)
where B1 and C1 are constants. Using vector potential defn. (Balanis), we
obtain
(27)
C1=Vi/2 (if Vi is the input voltage) and B1 is obtained from B.C. that
current vanishes at the ends. (27) is Hallén’s Integral equation for
perfectly conducting wire.
Hallén’s
Integral
Equation
Dr. Ashutosh Kedar

Source
Modeling
• Assumption that the wire is symmetrically fed by a voltage
source and the element acts as dipole antenna.
• Two methods to model the excitation at all points on the surface
of the dipole: -delta gap excitation and equivalent magnetic ring
current (or magnetic frill generator)
Fig.5Dr. Ashutosh Kedar

Over the annular aperture of the magnetic frill generator, the electric field is
represented by the TEM mode filed distribution of a coaxial transmission line
given by
(29)
Therefore the corresponding equivalent magnetic current density Mf for the
magnetic frill generator used to represent the aperture is equal to
(30)
5b
Dr. Ashutosh Kedar

• The fields generated by magnetic frill generator on the surface of
the wire
(31)
(31a)
The fields generated using (31) can be approximated by those found
along the axis (=0) leading to simpler form
(32)
(32a)
(32b)
Dr. Ashutosh Kedar

• Eqs (22), (24) and (27) have the form of
(33)
where F is known function g is response function and h is a known
excitation function. For (22) , F is an integro-differential operator while for
(24) and (27), its an integral operator.
Objective:- To determine g once F and h are specified.
Moment Method requires that the unknown response function may be
expanded as linear combination of N terms and written as
(34)
an are unknown constants and gn are basis or expansion functions. Hence
as explained in Part I of tut we get
(35)
The basis fns gn are chosen so that each F(gn)can be evaluated
conveniently, preferably in closed form or at the least numerically.
 Task is to find unknowns an.
-Expansion of (35) leads to one equation with N unknowns, not sufficient
to determine N unknowns an. Its necessary to have N linearly
independent equations.
-This can be done:-evaluating (35) (applying B.C.) at n different points.
This is point matching (or collocation). Doing this (35) becomes
(36)
Moment
Method
Solution
Dr. Ashutosh Kedar

• In matrix form
(37)
(37a)
(37b)
(37c)
The unknown coefficients can be obtained from matrix inversion
(38)
BASIS FUNCTIONS
The basis functions are chosen so that they have the ability to
accurately represent and resemble the anticipated unknown function,
while minimizing the computational effort.
Do not chose basis with smoother properties than unknowns being
represented.
Classification:-
1. Sub domain functions: - non-zero only over a part of domain of
the function g(x’); its domain is the surface of the structure. They
may be used without prior knowledge of the nature of function
they must represent unlike entire-domain functions.
2. Entire-domain functions:-exists over the entire domain of the
unknown function. Requires a priori knowledge of the nature of
the unknown function.
(39)
Dr. Ashutosh Kedar

(40)
Fig.6
Examples of Sub domain functions
Dr. Ashutosh Kedar

• To improve the point matching solution, an inner product may be defined
which is a scalar function satisfying
(44a)
(44b)
(44c)
(44d)
• Inner product may be typically defined as is
(45)
where w are weighting (testing) functions and S is the surface of structure
being analyzed. This technique is better known as method of moments.
•Point Matching (or collocation) method is a numerical technique whose solution
satisfy the em boundary conditions only at discrete points, in between it may not
satisfy, and the difference is called as residual. For half-wavelength dipole typical
residual is shown in Fig. 10a and for sinusoid –Galerkin’s method its shown in Fig.
10b (an improved one).
Weighting
functions
Dr. Ashutosh Kedar

• To minimize the residual in such a way that its overall average over
the entire structure approaches zero, the method of weighted
residuals is utilized in conjunction with the inner product. This
technique, called as Method of Moments, doesn’t lead to a vanishing
residual at every point on the surface of a conductor, but it forces it
the boundary conditions to be satisfied in an average sense over the
entire surface.
• MoM technique:- We define a set of N weighting (or testing)
functions, {wn}=w1,w2,…wN in the domain of operator F. Forming
inner product, (35) yields
(46)
In matrix form can be written as
(47)
(47a)
(47b)
The matrix may be solved for an by inversion (48)
Dr. Ashutosh Kedar

Dr. Ashutosh Kedar
• The choice of weighting fns is imp. In that the elements of {wn}
must be linearly independent, so that the N equations in (46) will
be linearly independent . Further it will generally be advantageous
to choose weighting fns. that minimize the computations required
to evaluate the inner products.
• The condition of linear independence between elements and the
advantage of computational simplicity are also important
characteristics of basis functions. Because of this similar types of
functions are used for both expansion and weighting functions.
• When wn=gn, its called Galerkin’s Technique.
• Note:- N2 terms to be evaluated in (47a). Each requires usually two
integrations: at least one to evaluate each F(gn) and one to perform
inner products of (45). This involves vast amount of computation
time.
• There is however a unique set of weighting functions that reduce
the number of required integrations-Dirac Delta Function
(49)
• where p specifies a position w.r.t. some reference (origin) and pm
represents a point at which the boundary condition is enforced.
(45) and (49) reduces (46) to
(50)

• Hence only integration left specified by F(gn). This simplification
won’t work with other weighting functions.
• Physically, the use of Dirac Delta fn. is seen as relaxation of B.C.
so that they are enforced only at discrete points on the surface of
the structure, hence called point matching.
• Programs in Matlab as well as Fortran are available to compute
self and mutual impedance of wire antennas in Antenna Theory:
Analysis and Design by Constantine Balanis.
• Any complex shape geometry can be analyzed using MOM.
• Commercial electromagnetic softwares based on Method of
Moments are available :-
– Zeland IE3D
– Sonnet EM
– ADS Momentum
– AWR EM Sight
– Ansoft Ensemble
– Ansoft Designer
– WIPL-D
– Concerto
Dr. Ashutosh Kedar

2. Analysis of Microstrip Patch Antenna using Zeland IE3D
Square microstrip patch antenna; L=29mm; Resonant frequency=2.45GHz; r=2.2
Dr. Ashutosh Kedar

IZ=0ohm
PNUM=1
RZ=50ohm
IZ=0ohm
PNUM=2
RZ=50ohm
P=p1
S=s1
W=w1
P=p2
S=s2
W=w2
P=p2
S=s2
W=w2
P=p1
S=s1
W=w1
1 2
W1=w1
W2=w2
1 2
W1=w1
W2=w2
3. Analysis of Band Pass Filter using Ansoft designer
Port1
Port2
Dr. Ashutosh Kedar

Mom slideshow

More Related Content

What's hot

Similar to Mom slideshow

Recently uploaded

Mom slideshow