Uploaded bynQuery
Minimizing Risk In Phase II and III Sample Size Calculation
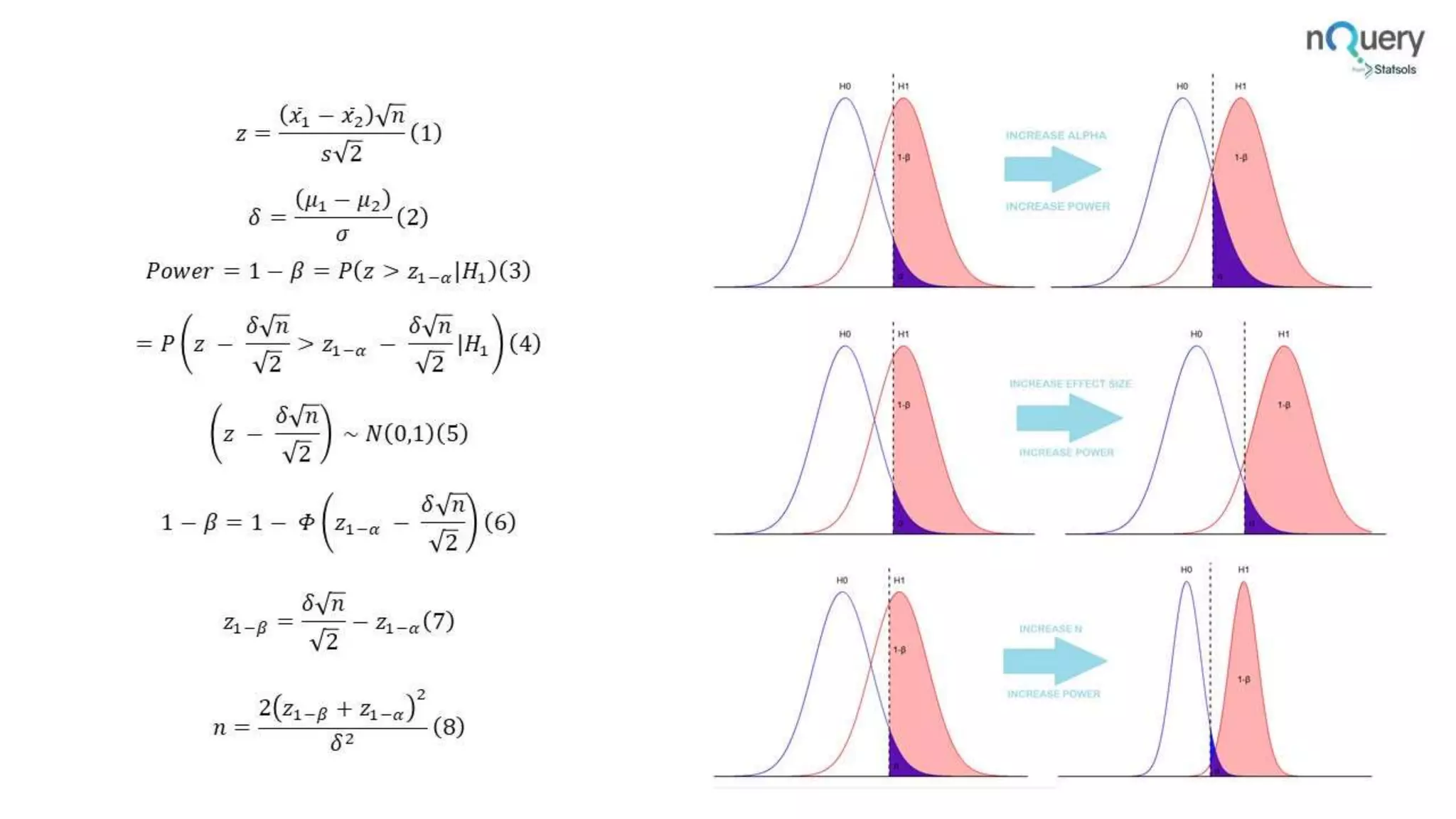
The document provides an overview of a webinar led by Ronan Fitzpatrick on sample size determination, emphasizing its importance in clinical trials. It covers methods such as Bayesian sample size determination, survival analysis, and the functionalities of the software nQuery, highlighting its user-friendly features and updates. Key topics include the calculation of required sample sizes for achieving statistical power and the relevance of estimating sample size to ensure valid conclusions in research.
More Related Content
Similar to Minimizing Risk In Phase II and III Sample Size Calculation
Minimizing Risk In Phase II and III Sample Size Calculation
- 2. WATCH THE WEBINAR Towatch the webinar, go to: http://bit.ly/2thIgmi
- 3. HOSTED BY: Ronan Fitzpatrick Head of Statistics FDA Guest Speaker nQuery Lead Researcher Guest Lecturer WEBINAR OVERVIEW – HOST
- 4. WEBINAR OVERVIEW –CONTENT CONTEN T> Introducing Sample Size Determination Bayesian Sample Size Determination Survival Analysis Demonstration Introducing nQuery Advanced
- 5.
- 6. WHAT IS SAMPLESIZE ESTIMATION? The process for finding the appropriate sample size for your study. The most common metric for this is statistical power The power is the probability that the study will be able to detect a true effect of a specified size. In other words, Power is the probability of rejecting the null hypothesis when it is false
- 7. 𝑧 = 𝑥1 −𝑥2 𝑛 𝑠 2 1 𝛿 = 𝜇1 − 𝜇2 𝜎 2 𝑃𝑜𝑤𝑒𝑟 = 1 − 𝛽 = 𝑃 𝑧 > 𝑧1−𝛼 𝐻1 3 = 𝑃 𝑧 − 𝛿 𝑛 2 > 𝑧1−𝛼 − 𝛿 𝑛 2 |𝐻1 4 𝑧 − 𝛿 𝑛 2 ~ 𝑁 0,1 5 1 − 𝛽 = 1 − 𝛷 𝑧1−𝛼 − 𝛿 𝑛 2 6 𝑧1−𝛽 = 𝛿 𝑛 2 − 𝑧1−𝛼 7 𝑛 = 2 𝑧1−𝛽 + 𝑧1−𝛼 2 𝛿2 8
- 8. WHY ESTIMATE SAMPLE SIZE? Crucialto Arrive at Valid Conclusions Reduce Chance of Large Errors (Type S/M Errors) Balance Ethical and Practical Considerations Both how many needed and how many not needed! Standard Trial Design Requirement EMA, FDA, Nature Group Publishing Guidelines etc. But Many Studies Still have Low Power Can’t Rely on Past Studies (Crisis of
- 9. 5 ESSENTIAL STEPSFOR SAMPLE SIZE 1 Formulate the study Study question, primary outcome, statistical method 2 Specify analysis parameters Standard deviation, ICC, dispersion 3 Specify the Effect Size for Test Expected/targeted difference or ratio 4 Compute Sample Size N for specified power or power for
- 10. INTRODUCING nQUERY Over 20Years of Experience in Sample Size Determination and Power Analysis for Clinical Trials Latest Release had Methods for ~250 Trial Designs Used by 45/50 Top Pharma and Biotech Companies nQuery’s 20 Years of Success is Based on 1. Being Easy to Use and Accessible to All Users
- 11. Part II Bayesian SampleSize Determination
- 12. BAYESIAN ANALYSIS Bayesian Analysiscontinues to grow in popularity in statistical analysis in clinical trials Offers ability to integrate domain knowledge and prior study data for more efficient and accurate testing For sample size determination, two broad schools: 1. Sample Size for Bayesian Methods 2. Bayesian Approaches to Improve Sample Size
- 13. BAYESIAN SAMPLE SIZE 1.Sample Size for Bayesian Methods Sample size for specific values of Bayesian parameters e.g. Bayes Factors, Credible Intervals, Posterior Probability 2. Bayesian Approaches to Improve Sample Size Integrating Bayesian methods into current methods to add greater context for parameter uncertainty
- 14. ASSURANCE EXAMPLE “The outcomevariable … is reduction in CRP after four weeks relative to baseline, and the principal analysis will be a one-sided test of superiority at the 2.5% significance level. The (two) population variance … is assumed to be … equal to 0.0625. … the test is required to have 80% power to detect a treatment effect of 0.2, leading to a proposed trial size of n1 = n2 = 25 patients … For the calculation of assurance, we suppose that the elicitation of prior information … gives the mean of 0.2 and variance of 0.0625. If we assume a normal prior distribution, we can compute assurances with m = 0:2, v = 0.06 … Source: Wiley.com Parameter Value Significance Level (One- Sided) 0.05 Prior Mean Difference 0.2 Prior Difference Variance 0.06 Posterior Standard Deviation √0.0625=0.25 Sample Size per Group 25
- 15.
- 16. SAMPLE SIZE FORSURVIVAL ANALYSIS Survival Analysis is about the expected duration of time to an event (e.g. patient death) Common methods include linear-rank tests and Cox Regression Power is related to number of events, not sample size Sample Size = Subjects to get no. of events in study duration Can Account explicitly for accrual time and dropout Can be interested in varying hazards ratio, follow-up time etc.
- 17. SURVIVAL ANALYSIS EXAMPLE“Using anunstratified log-rank test at the one-sided 2.5% significance level, a total of 282 events would allow 92.6% power to demonstrate a 33% risk reduction (hazard ratio for RAD/placebo of about 0.67, as calculated from an anticipated 50% increase in median PFS, from 6 months in placebo arm to 9 months in the RAD001 arm). With a uniform accrual of approximately 23 patients per month over 74 weeks and a minimum follow up of 39 weeks, a total of 352 patients would be required to obtain 282 PFS events, assuming an exponential progression-free survival distribution with a median of 6 months in the Placebo arm and of 9 months in Source: nejm.org Parameter Value Significance Level (One-Sided) 0.025 Placebo Median Survival (months) 6 Everolimus Median Survival (months) 9 Hazard Ratio 0.6666 7 Accrual Period (Weeks) 74 Minimum Follow-Up (Weeks) 39
- 18.
- 19. nQUERY ADVANCED nQuery Advancedis the leading sample size and power calculation software used for clinical trials Regulatory Qualification Just Got Easier Survival Analysis Just Got Stronger nQuery Interface Just Got Cleaner New Platform New Collaboration What’s new in nQuery Advanced? 17 New Tables Sample Size Assistance Module add-ons & HubIQ/OQ Tools
- 20. THANK YOU •nQuery Advancedwill be released August 2017 •You will automatically be upgraded to nQuery Advanced if purchased before then •Contact sales@statsols.com for updates, upgrade details and for any further info
Editor's Notes
- #3 Appropriate would usually be defined in terms of preventing too low sample size, though too high has practical costs. Other metrics include confidence interval width (precision), cost based and Bayesian methods. Important to note that you need to specify an exact value for the effect even though alternative hypothesis acceptance space can technically can be any non-null hypothesis point value (commonly any non-zero value) Can be though of as the area of the alternative pdf which is contained within the rejection region of the null hypothesis. Interesting to note that power of 50% is equivalent to lower limit of CI being equal to zero for zero-based z-statistic null
- #7 Appropriate would usually be defined in terms of preventing too low sample size, though too high has practical costs. Other metrics include confidence interval width (precision), cost based and Bayesian methods. Important to note that you need to specify an exact value for the effect even though alternative hypothesis acceptance space can technically can be any non-null hypothesis point value (commonly any non-zero value) Can be though of as the area of the alternative pdf which is contained within the rejection region of the null hypothesis. Interesting to note that power of 50% is equivalent to lower limit of CI being equal to zero for zero-based z-statistic null
- #9 Point 1: http://rsos.royalsocietypublishing.org/content/1/3/140216 -> Screening problem analogy. Type S Error = Sign Error i.e. sign of estimate is different than actual population value Type M Error = Magnitude Error i.e. estimate is order of magnitude different than actual value Point 2: Know we have only 100 subjects available. Need to know what power will this give us, i.e. is there enough power to justify even doing the study. Stage III clinical trials constitute 90% of trial costs, vital to reduce waste and ensure can fulfil goal. Point 3: Sample Size requirements described in ICH Efficacy Guidelines 9: STATISTICAL PRINCIPLES FOR CLINICAL TRIALS See FDA/NIH draft protocol template here: http://osp.od.nih.gov/sites/default/files/Protocol_Template_05Feb2016_508.pdf (Section 10.5) Nature Statistical Checklist: http://www.nature.com/nature/authors/gta/Statistical_checklist.doc Point 4: In Cohen’s (1962) seminal power analysis of the journal of Abnormal and Social Psychology he concluded that over half of the published studies were insufficiently powered to result in statistical significance for the main hypothesis. Many journals (e.g. Nature) now require that authors submit power estimates for their studies. Power/Sample size one of areas highlighted when discussing “crisis of reproducibility” (Ioannidis). Relatively easy fix compared to finding p-hacking etc.
- #10 More detail available on our website via a whitepaper.
- #14 Alternative linear rank tests include Tahone-Ware, Gehan. Planned for next release circa. Summer 2016. Sample size mainly asking “How many subjects needed to attain X events?” Most methods optimised for exponential survival but could enter piece-wise linear approximation of probability at time t for other distributions (e.g. Weibull) Analytic vs Simulation = Much wider debate. Usually have ease of use vs flexibility trade-off. Simulation better suited to programming environment e.g. R
- #17 Alternative linear rank tests include Tahone-Ware, Gehan. Planned for next release circa. Summer 2016. Sample size mainly asking “How many subjects needed to attain X events?” Most methods optimised for exponential survival but could enter piece-wise linear approximation of probability at time t for other distributions (e.g. Weibull) Analytic vs Simulation = Much wider debate. Usually have ease of use vs flexibility trade-off. Simulation better suited to programming environment e.g. R
- #20 Alternative linear rank tests include Tahone-Ware, Gehan. Planned for next release circa. Summer 2016. Sample size mainly asking “How many subjects needed to attain X events?” Most methods optimised for exponential survival but could enter piece-wise linear approximation of probability at time t for other distributions (e.g. Weibull) Analytic vs Simulation = Much wider debate. Usually have ease of use vs flexibility trade-off. Simulation better suited to programming environment e.g. R