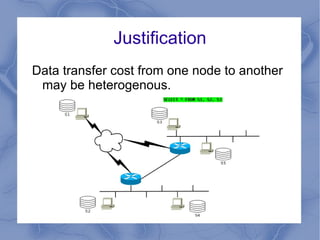
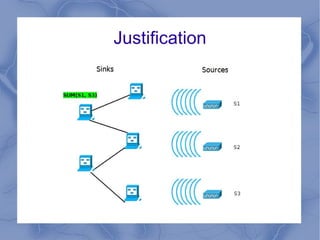
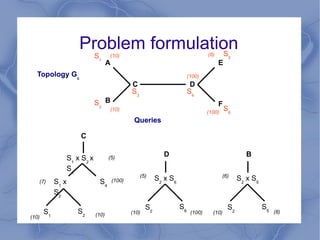
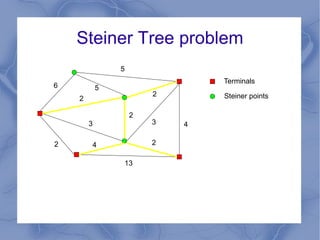
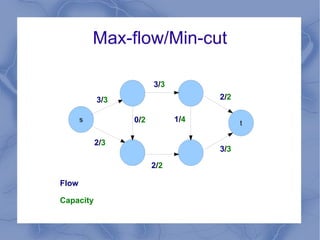
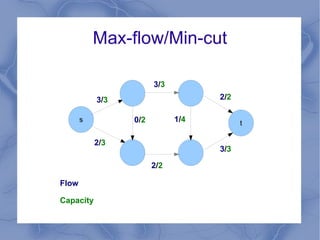
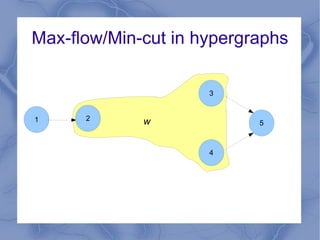
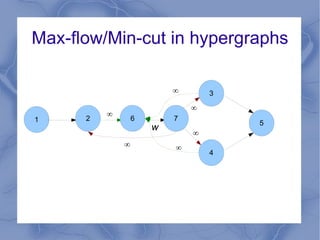
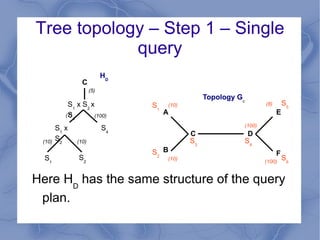
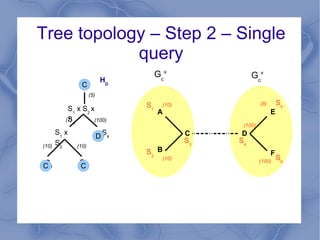
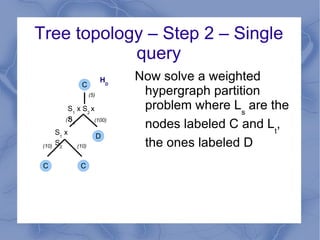
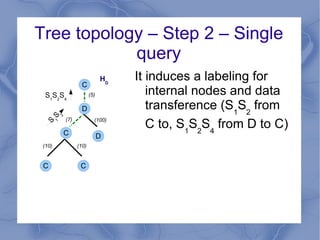
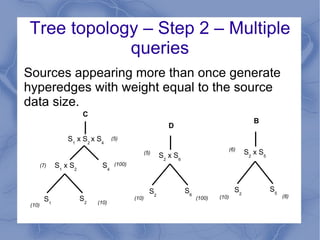
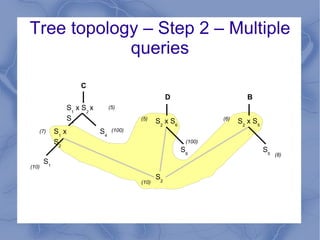
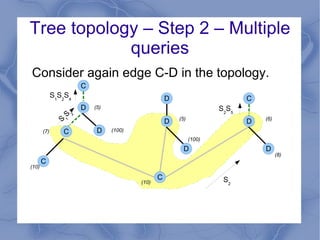
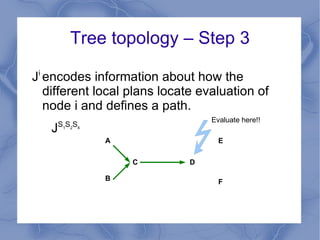
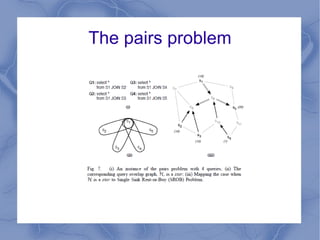
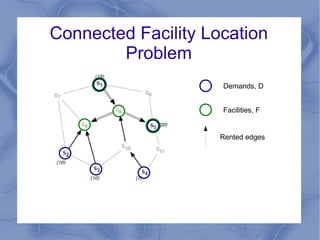
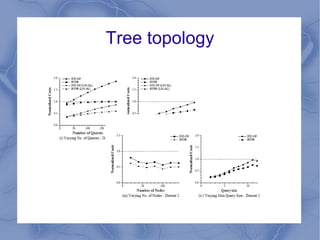
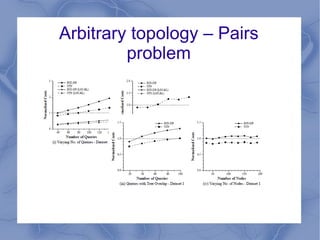
The document discusses the challenge of minimizing communication costs in distributed multi-query processing using graph theory concepts. It outlines the problem formulation, proposed methods, and analysis involving various topologies, emphasizing the NP-hard nature of the data movement minimization problem and the availability of approximation algorithms. Experimental results demonstrate the effectiveness of the proposed multi-query approach in comparison to isolated optimization strategies.

1. Minimizing Communication Cost in Distributed Multi-query Processing Jian Li, Amol Deshpande, Samir Khuller Department of Computer Science, University of Maryland Presented by: Luis Galárraga Saarland University July 7th, 2010

2. Outline Justification and related work

3. Problem formulation

4. Proposed methods and analysis Graph theory concepts

5. Tree topology

6. Arbitrary graph topologies

7. Experimental results Conclusions

8. Outline Justification Problem formulation

9. Proposed methods and analysis Graph theory concepts

10. Tree topology

11. Arbitrary graph topologies

12. Experimental results Conclusions

13. Justification Emergence of large-scale distributed query processing in applications like: Wireless sensor networks

14. Publish-subscribe systems

15. Distributed stream processing applications Common need: Minimize data movement!!

16. Justification Data transfer cost from one node to another may be heterogenous.

17. Justification

18. Outline Justification Problem formulation Proposed methods and analysis Graph theory concepts

19. Tree topology

20. Arbitrary graph topologies

21. Experimental results Conclusions

22. Problem formulation Minimization of data movement for multiples queries.

23. Assumptions: Non-uniform communication cost model.

24. No restrictions on data size.

25. Query plans are part of the input.

26. Intermediate results sizes are known.

27. More formally Input: Set of relations or data sources

28. Topology, undirected weighted graph

29. Assignment of relations to nodes in the topology.

30. More formally Set of queries

31. Each query comes with a plan in the form of a directed tree. Destination node Data sources involved Data size S i S j S i x S j w z(S i ) z(S j ) z(S i x S j )

32. More formally Given the topology graph G c and a set of trees representing the query plans, our goal is to find a data movement plan that minimizes the total communication cost incurred while executing the queries.

33. Problem formulation Topology G c Queries (10) S 1 S 2 S 1 x S 2 C (10) (7) S 4 S 1 x S 2 x S 4 (5) (100) (100) S 2 S 6 S 2 x S 6 D (10) (5) S 2 S 5 S 2 x S 5 B (10) (6) (8) B A C D E F S 2 S 1 S 3 S 4 S 6 S 5 (10) (10) (100) (8) (100)

34. Problem formulation If a block of data sized S is sent along an edge e with weight w(e) then the communication cost is S * w(e)

35. For simplicity in the examples assume w(e) = 1 for all edges. But the algorithm is general in that sense!

36. Outline Justification

37. Problem formulation

38. Proposed methods and analysis Graph theory concepts Tree topology

39. Arbitrary graph topologies

40. Experimental results Conclusions

41. Problem analysis It has been proved to be NP-Hard Via reduction to the Steiner Tree problem Is everything lost? If topology graph is a tree, there is a polynomial-time algorithm.

42. For general topologies, aproximation algorithms are known.

43. Steiner Tree problem Given an undirected graph:

44. Find a tree of minimum weight that connects all vertices in S. It can contain vertices not in S, known as Steiner points.

45. Steiner Tree problem 5 5 2 6 2 2 3 4 13 2 2 3 4 Terminals Steiner points

46. The algorithm It implies to solve a series of min-cut problems on appropriately constructed hypergraphs . Umm.. Hypergraphs?

47. Hypergraphs Generalization of a graph. In normal graphs, edges can be seen as pairs of vertices.

48. Hyperedges can group any number of vertices.

49. Max-flow/Min-cut Given a weighted, directed graph and nodes s , t known as source and sink:

50. Find a flow or mapping of maximum value:

51. Max-flow/Min-cut 3 / 3 2 / 3 2 / 2 3 / 3 0 / 2 1 / 4 2 / 2 3 / 3 Flow Capacity

52. Max-flow/Min-cut A min-cut is a set of edges with minimum weight such that if removed from the graph, there is no path from s to t.

53. The maximum value of an s-t flow is equal to the minimum capacity of an s-t cut.

54. Max-flow/Min-cut 3 / 3 2 / 3 3 / 3 0 / 2 1 / 4 2 / 2 3 / 3 2 / 2 Flow Capacity

55. Max-flow/Min-cut in hypergraphs Problem solvable in polynomial time.

56. What about max-flow in hypergraphs? For every hyperedge, add two new nodes and a directed edge between them of capacity equal to the weight of the hyperedge.

57. Max-flow/Min-cut in hypergraphs w