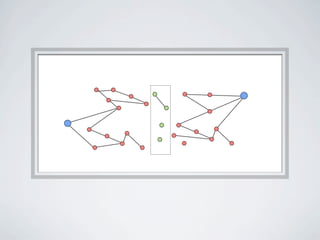
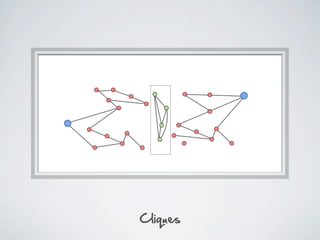
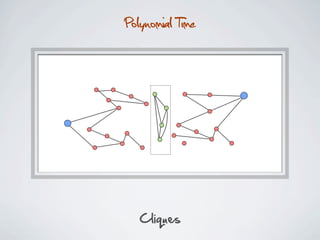
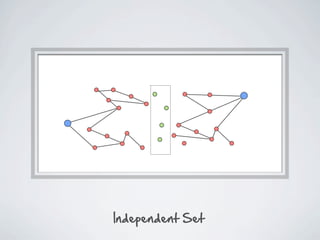
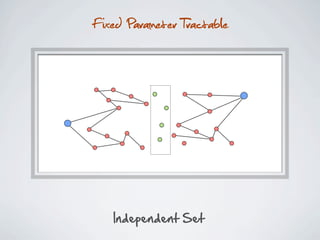
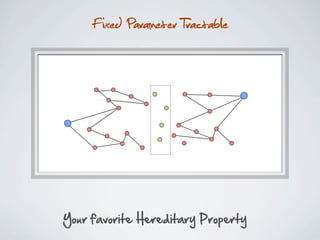
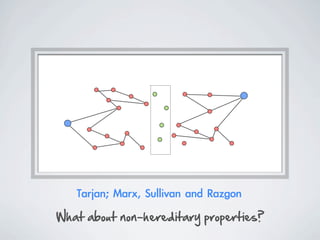
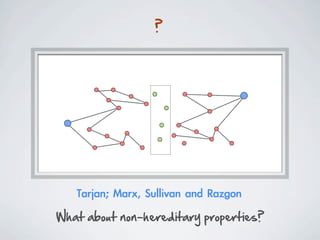
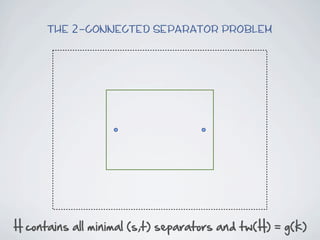
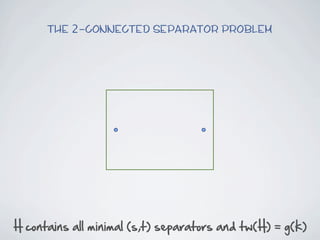
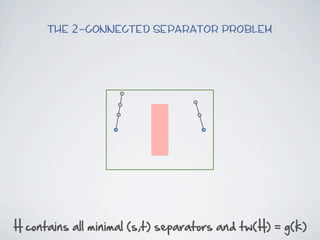
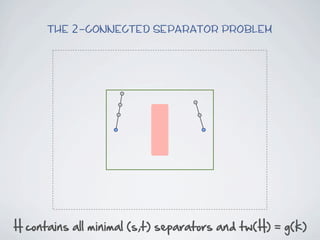
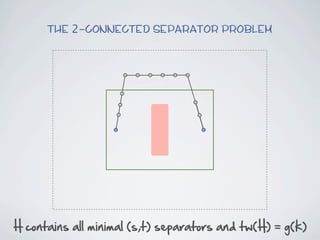
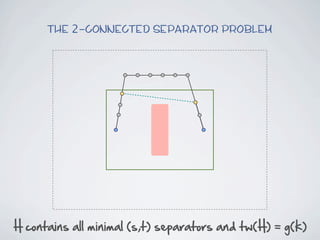
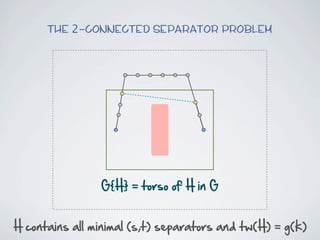
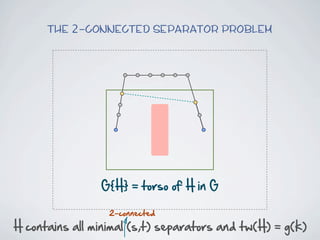
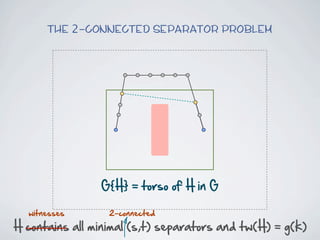
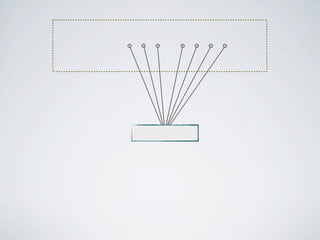
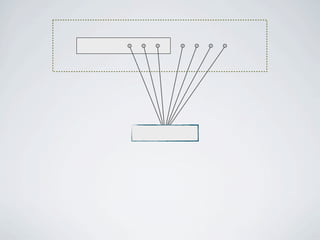
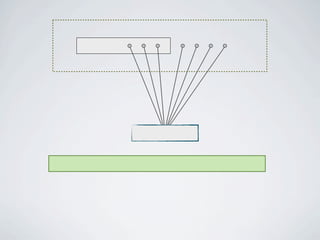
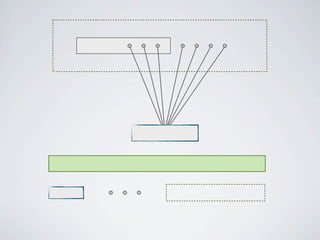
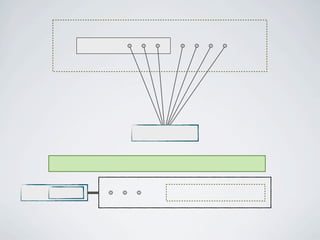
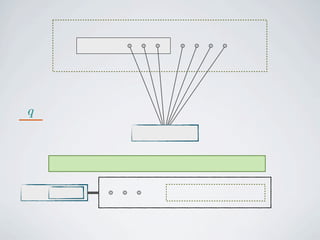
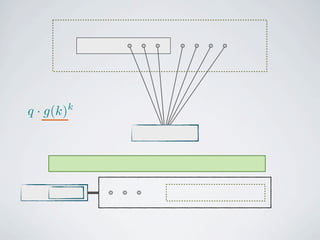
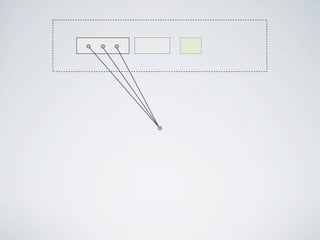
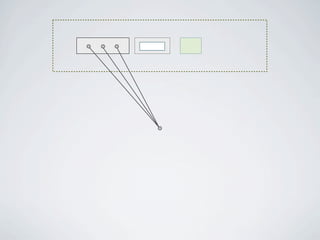
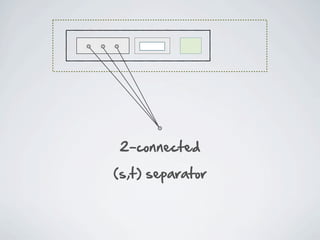
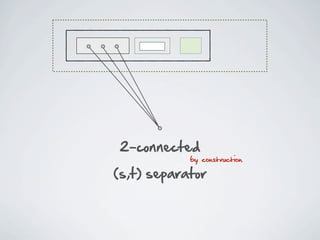
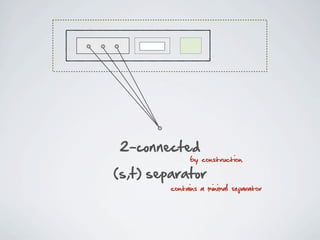
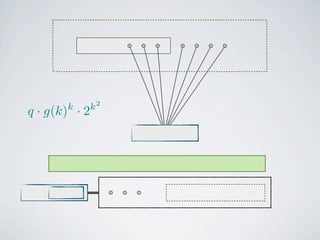
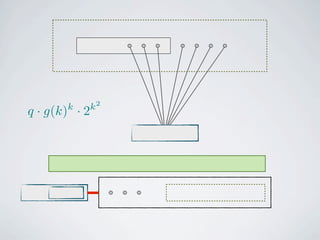
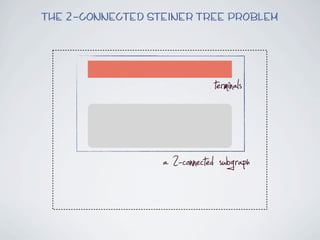
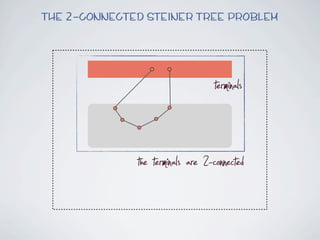
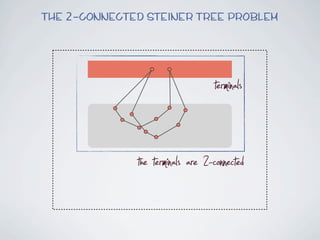
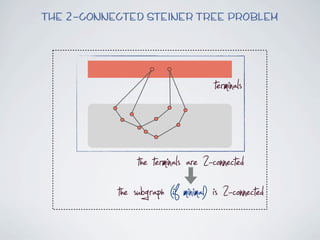
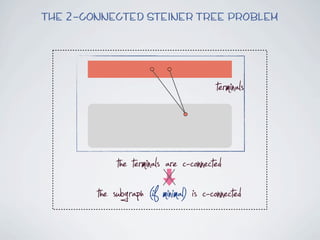
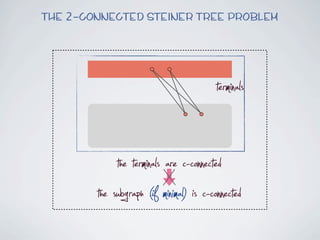
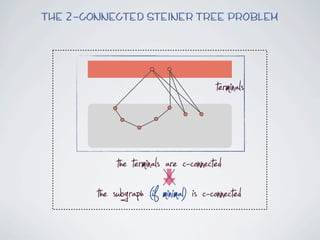
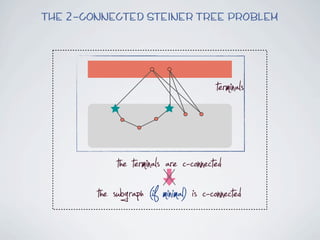
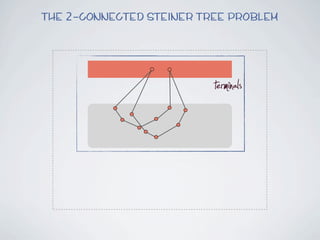
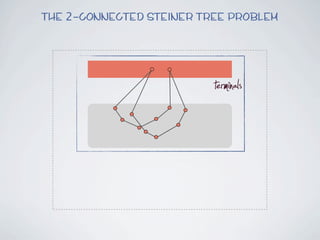
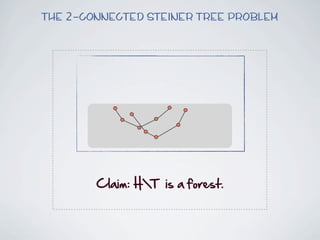
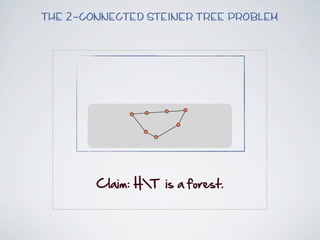
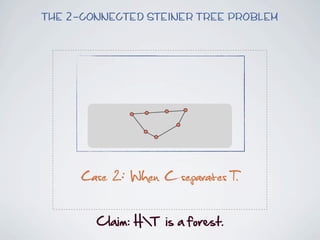
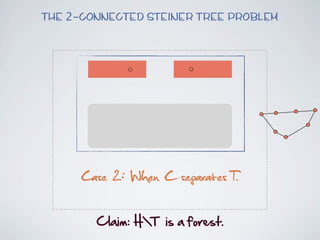
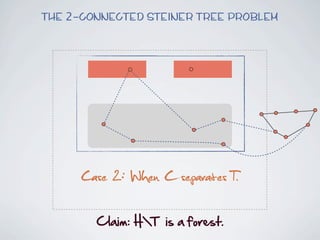
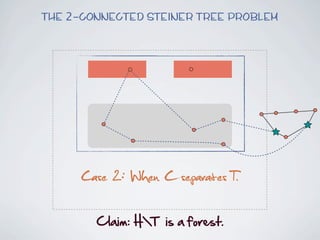
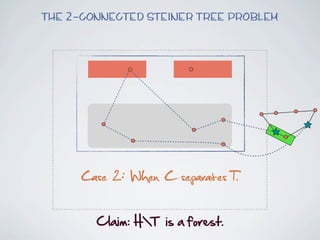
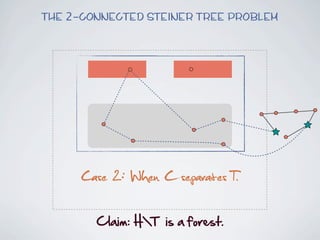
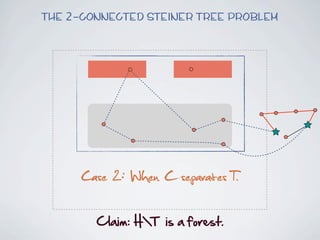
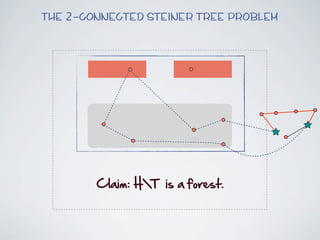
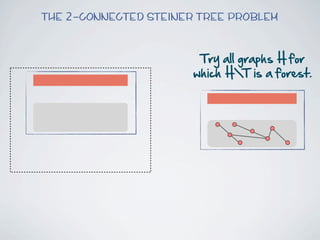
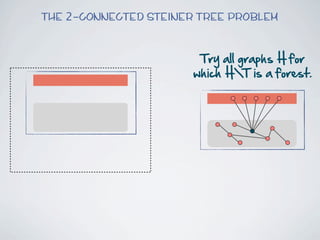
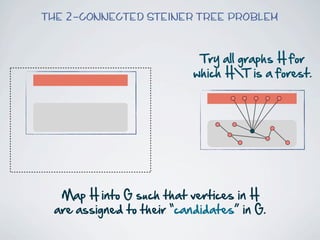
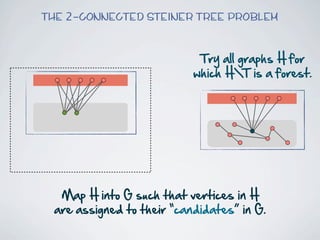
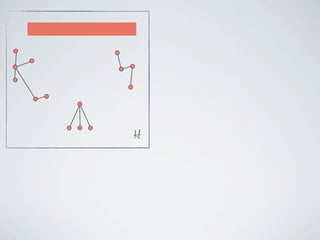
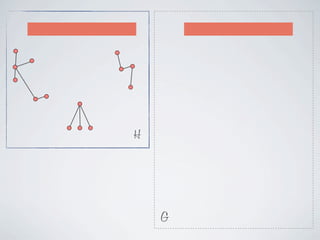
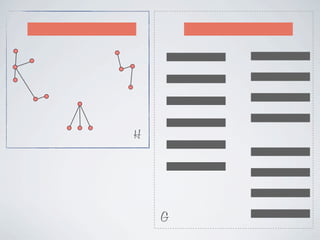
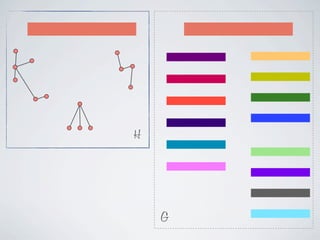
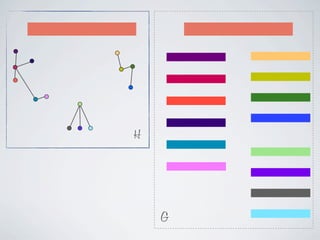
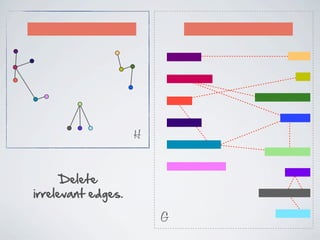
The document discusses connected separators and 2-connected separators in graphs. It presents the treewidth reduction theorem, which shows that the 2-connected separator problem can be solved by finding an equivalent instance on a graph of small treewidth. It also discusses properties of 2-connected Steiner trees, including that the non-terminal vertices induce a forest, and presents an algorithm that guesses and maps the structure of the 2-connected Steiner tree.

1. separators

2. separators
with non-hereditary properties

3. separators
with non-hereditary properties
Pinar Heggernes, Pim van’t Hof, Dániel Marx, and Yngve Villanger

5. OJ`çååÉÅíÉÇ=pÉé~ê~íçêë

6. OJ`çååÉÅíÉÇ=pÉé~ê~íçêë
The Treewidth Reduction Theorem

7. OJ`çååÉÅíÉÇ=pÉé~ê~íçêë
The Treewidth Reduction Theorem
OJ`çååÉÅíÉÇ=píÉáåÉê=qêÉÉë

8. OJ`çååÉÅíÉÇ=pÉé~ê~íçêë
The Treewidth Reduction Theorem
OJ`çååÉÅíÉÇ=píÉáåÉê=qêÉÉë
Some Structural Observations

10. PRELIMINARIES

16. Cliques

17. Polynomial Time
Cliques

18. Independent Set

19. Fixed Parameter Tractable
Independent Set

20. Fixed Parameter Tractable
Your favorite Hereditary Property

21. Fixed Parameter Tractable
Tarjan; Marx, Sullivan and Razgon
Your favorite Hereditary Property

22. Tarjan; Marx, Sullivan and Razgon
What about non-­hereditary properties?

23. ?
Tarjan; Marx, Sullivan and Razgon
What about non-­hereditary properties?

24. Connected Separators

25. 2- Connected Separators

26. c - Connected Separators

27. c - Connected Separators
0- Regular Separators

28. c - Connected Separators
c -Regular Separators

29. c - Connected Separators
c -Regular Separators
1-Diameter Separators

30. c - Connected Separators
c -Regular Separators
c -Diameter Separators

32. 2-CONNECTED SEPARATORS

33. The 2-connected Separator Problem

34. The 2-connected Separator Problem

35. The 2-connected Separator Problem
A (s,t) separator of size at most k
that induces a 2-­connected subgraph.

36. The 2-connected Separator Problem
“Easy” on graphs of small treewidth.
(Due to MSO expressibility.)

37. The 2-connected Separator Problem
“Easy” on graphs of small treewidth.
(Due to MSO expressibility.)
General graphs
Equivalent instances with small
treewidth

38. The 2-connected Separator Problem
The Treewidth Reduction
Theorem
General graphs
Equivalent instances with small
treewidth

39. The 2-connected Separator Problem

40. The 2-connected Separator Problem

41. The 2-connected Separator Problem
H contains all minimal (s,t) separators and tw(H) = g(k)

42. The 2-connected Separator Problem
H contains all minimal (s,t) separators and tw(H) = g(k)

43. The 2-connected Separator Problem
H contains all minimal (s,t) separators and tw(H) = g(k)

44. The 2-connected Separator Problem
H contains all minimal (s,t) separators and tw(H) = g(k)

45. The 2-connected Separator Problem
H contains all minimal (s,t) separators and tw(H) = g(k)

46. The 2-connected Separator Problem
H contains all minimal (s,t) separators and tw(H) = g(k)

47. The 2-connected Separator Problem
G{H} = torso of H in G
H contains all minimal (s,t) separators and tw(H) = g(k)

48. The 2-connected Separator Problem
G{H} = torso of H in G
2-­connected
H contains all minimal (s,t) separators and tw(H) = g(k)

49. The 2-connected Separator Problem
G{H} = torso of H in G
witnesses 2-­connected
H contains all minimal (s,t) separators and tw(H) = g(k)

60. k k2
q · g(k) · 2

61. k k2
q · g(k) · 2

62. k k2
q · g(k) · 2

63. k k2
q · g(k) · 2

71. 2-­connected
(s,t) separator

72. 2-­connected
by construction
(s,t) separator

73. 2-­connected
by construction
(s,t) separator
contains a minimal separator

74. `
k k2
q · g(k) · 2

75. `
k k2
q · g(k) · 2

78. 2-CONNECTED STEINER TREE

79. The 2-connected Steiner Tree Problem
Some structural Discoveries
An Algorithm

80. The 2-connected Steiner Tree Problem

81. The 2-connected Steiner Tree Problem

82. The 2-connected Steiner Tree Problem

83. The 2-connected Steiner Tree Problem
terminals

84. The 2-connected Steiner Tree Problem
terminals

85. The 2-connected Steiner Tree Problem
terminals
a 2-connected subgraph

86. The 2-connected Steiner Tree Problem
terminals
the terminals are 2-connected

87. The 2-connected Steiner Tree Problem
terminals
the terminals are 2-connected

88. The 2-connected Steiner Tree Problem
terminals
the terminals are 2-connected

89. The 2-connected Steiner Tree Problem
terminals
the terminals are 2-connected

90. The 2-connected Steiner Tree Problem
terminals
the terminals are 2-connected
the subgraph (if minimal) is 2-connected

91. The 2-connected Steiner Tree Problem
terminals

92. The 2-connected Steiner Tree Problem
terminals
the terminals are c-connected
the subgraph (if minimal) is c-connected

93. The 2-connected Steiner Tree Problem
terminals
the terminals are c-connected
the subgraph (if minimal) is c-connected

94. The 2-connected Steiner Tree Problem
terminals
the terminals are c-connected
the subgraph (if minimal) is c-connected

95. The 2-connected Steiner Tree Problem
terminals
the terminals are c-connected
the subgraph (if minimal) is c-connected

96. The 2-connected Steiner Tree Problem
terminals
the terminals are c-connected
the subgraph (if minimal) is c-connected

97. The 2-connected Steiner Tree Problem
terminals

98. The 2-connected Steiner Tree Problem
terminals

99. The 2-connected Steiner Tree Problem
Claim: HT is a forest.

100. The 2-connected Steiner Tree Problem
Claim: HT is a forest.

101. The 2-connected Steiner Tree Problem
Case 1: When C does not separate T.
Claim: HT is a forest.

102. The 2-connected Steiner Tree Problem
Case 1: When C does not separate T.
Claim: HT is a forest.

103. The 2-connected Steiner Tree Problem
Case 2: When C separates T.
Claim: HT is a forest.

104. The 2-connected Steiner Tree Problem
Case 2: When C separates T.
Claim: HT is a forest.

105. The 2-connected Steiner Tree Problem
Case 2: When C separates T.
Claim: HT is a forest.

106. The 2-connected Steiner Tree Problem
Case 2: When C separates T.
Claim: HT is a forest.

107. The 2-connected Steiner Tree Problem
Case 2: When C separates T.
Claim: HT is a forest.

108. The 2-connected Steiner Tree Problem
Case 2: When C separates T.
Claim: HT is a forest.

109. The 2-connected Steiner Tree Problem
Case 2: When C separates T.
Claim: HT is a forest.

110. The 2-connected Steiner Tree Problem
Claim: HT is a forest.

111. The 2-connected Steiner Tree Problem

112. The 2-connected Steiner Tree Problem

113. The 2-connected Steiner Tree Problem

114. The 2-connected Steiner Tree Problem
Guess the structure of H.

115. The 2-connected Steiner Tree Problem
Try all graphs H for
which HT is a forest.

116. The 2-connected Steiner Tree Problem
Try all graphs H for
which HT is a forest.

117. The 2-connected Steiner Tree Problem
Try all graphs H for
which HT is a forest.
Map H into G such that vertices in H
are assigned to their “candidates” in G.

118. The 2-connected Steiner Tree Problem
Try all graphs H for
which HT is a forest.
Map H into G such that vertices in H
are assigned to their “candidates” in G.

119. H

120. H
G

121. H
G

122. H
G

123. H
G

124. H
Prune the color
classes to get rid of
non-­candidates.
G

125. H
Delete
irrelevant edges.
G

126. H
Perform
a breadth-­first
search.
G