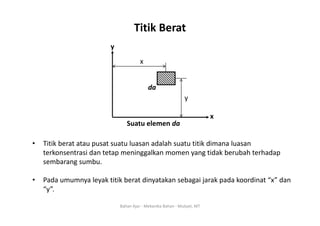
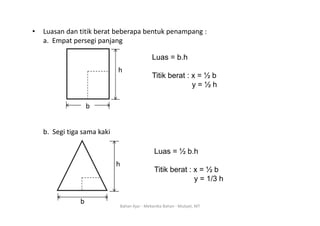
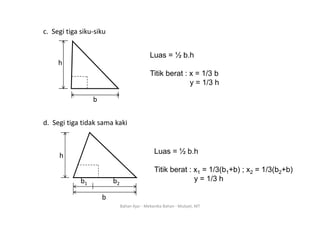
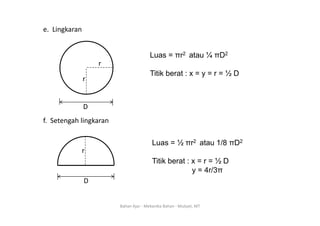
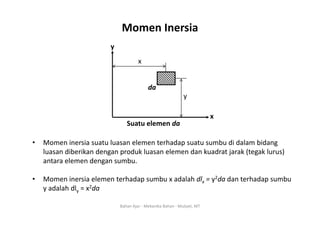
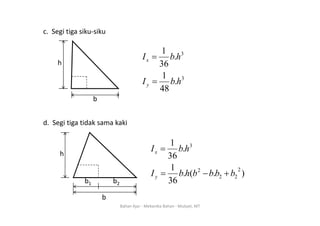
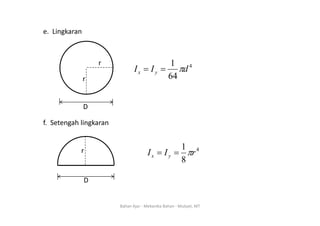
Dokumen ini membahas konsep titik berat dan momen inersia dari berbagai bentuk penampang dalam mekanika bahan. Titik berat didefinisikan sebagai koordinat (x, y) di mana luasan terkonsentrasi, sedangkan momen inersia adalah produk antara luasan dan kuadrat jarak dari elemen terhadap sumbu. Informasi ini juga mencakup rumus-rumus untuk menghitung titik berat dan momen inersia dari berbagai bentuk geometri seperti persegi panjang, segitiga, dan lingkaran.

1. Titik Berat
x
y
x
da
y
da
x
Suatu elemen da
• Titik berat atau pusat suatu luasan adalah suatu titik dimana luasan
terkonsentrasi dan tetap meninggalkan momen yang tidak berubah terhadap
sembarang sumbu.
g
• Pada umumnya leyak titik berat dinyatakan sebagai jarak pada koordinat “x” dan
“y”
y .
Bahan Ajar ‐ Mekanika Bahan ‐ Mulyati, MT

2. • Momen pertama luasan elemen da terhadap sumbu x adalah dQx = yda dan
terhadap sumbu y adalah dQy = xda
• Selanjutnya momen pertama luasan terhingga dinyatakan dengan :
j y p gg y g
∫
∫
= x
X
dQ
Q
dQ
Q
• Jadi letak titik berat atau pusat suatu luasan dengan koordinat sebagai berikut :
∫
= y
y dQ
Q
• Jadi letak titik berat atau pusat suatu luasan dengan koordinat sebagai berikut :
Q
xda
∫
Q
yda
A
Q
A
xda
x
y
=
=
∫
∫
A
Q
A
yda
y x
=
= ∫
dimana A adalah luasan
Bahan Ajar ‐ Mekanika Bahan ‐ Mulyati, MT

3. • Luasan dan titik berat beberapa bentuk penampang :
a. Empat persegi panjang
Luas = b.h
h
Titik berat : x = ½ b
y = ½ h
b
y
b. Segi tiga sama kaki
h
Luas = ½ b.h
h
Titik berat : x = ½ b
y = 1/3 h
b
Bahan Ajar ‐ Mekanika Bahan ‐ Mulyati, MT

4. c. Segi tiga siku‐siku
Luas = ½ b.h
h
Titik berat : x = 1/3 b
y = 1/3 h
h
b
d. Segi tiga tidak sama kaki
Luas = ½ b.h
h
Titik berat : x1 = 1/3(b1+b) ; x2 = 1/3(b2+b)
y = 1/3 h
b1 b2
b
Bahan Ajar ‐ Mekanika Bahan ‐ Mulyati, MT

5. e. Lingkaran
Luas = πr2 atau ¼ πD2
Titik berat : x = y = r = ½ D
r
r
D
f. Setengah lingkaran
Luas = ½ πr2 atau 1/8 πD2
Titik berat : x = r = ½ D
r
y = 4r/3π
D
Bahan Ajar ‐ Mekanika Bahan ‐ Mulyati, MT

6. • Untuk luasan bidang yang tersusun atas n sub‐luasan Ai, dengan masing‐masing
koordinat “x” dan “y” diketahui, titik berat dapat ditentukan dengan cara
menganggap luasan penampang sebagai berat, kemudian berdasarkan jumlah
momen dari bagian‐bagian luasan penampang terhadap garis sembarang sama
g g p p g p g g
dengan momen keseluruhan penampang terhadap garis yang sama, maka letak
titik berat dapat ditentukan :
⎞
⎛ ⎞
⎛
dan
x
A
x
A
n
i
i
n
i
i
i ⎟
⎠
⎞
⎜
⎝
⎛
= ∑
∑ =
= 1
1
. y
A
y
A
n
i
i
n
i
i
i ⎟
⎠
⎞
⎜
⎝
⎛
= ∑
∑ =
= 1
1
.
sehingga,
∑
=
n
i
i
i A
x
1
. ∑
n
i
i
i A
y
1
.
dan
∑
=
= n
i
i
i
i
A
x
1
1
∑
=
=
= n
i
i
i
i
A
y
1
1
=
i 1
Bahan Ajar ‐ Mekanika Bahan ‐ Mulyati, MT

7. Momen Inersia
y
x
da
x
da
y
x
Suatu elemen da
• Momen inersia suatu luasan elemen terhadap suatu sumbu di dalam bidang
luasan diberikan dengan produk luasan elemen dan kuadrat jarak (tegak lurus)
antara elemen dengan sumbu.
g
• Momen inersia elemen terhadap sumbu x adalah dlx = y2da dan terhadap sumbu
y adalah dl = x2da
y adalah dly x da
Bahan Ajar ‐ Mekanika Bahan ‐ Mulyati, MT

8. • Momen inersia suatu luasan terhingga terhadap suatu sumbu di dalam bidang
luasan diberikan dengan jumlah momen inersia terhadap sumbu yang sama dari
luasan diberikan dengan jumlah momen inersia terhadap sumbu yang sama dari
seluruh elemen yang ada pada luasan terhingga tersebut, dinyatakan dalam
bentuk integral :
dan
∫ ∫
=
= da
y
dl
I x
x
2
∫ ∫
=
= da
x
dl
I y
y
2
• Untuk suatu bidang yang tersusun atas n sub‐bidang Ai , dimana masing‐masing
momen inersianya terhadap sumbu x dan sumbu y diketahui, maka bentuk
y p y
integral dapat diganti dengan bentuk penjumlahan :
∑
n
I
I )
( ∑
n
dan
∑
=
=
i
i
x
x I
I
1
)
( ∑
=
=
i
i
y
y I
I
1
)
(
• Satuan untuk momen inersia adalah pangkat empat dari satuan panjang.
Bahan Ajar ‐ Mekanika Bahan ‐ Mulyati, MT

9. • Momen inersia terhadap sumbu yang melalui titik berat beberapa bentuk
penampang :
a. Empat persegi panjang
h
3
1
.
12
1
h
b
Ix =
3
.
12
1
b
h
Iy =
b S i i k ki
b
b. Segi tiga sama kaki
3
.
36
1
h
b
Ix =
h
3
.
48
1
36
h
b
Iy =
b
48
Bahan Ajar ‐ Mekanika Bahan ‐ Mulyati, MT

10. c. Segi tiga siku‐siku
h
3
.
36
1
h
b
Ix =
h
3
.
48
1
36
h
b
Iy
x
=
b
48
y
d. Segi tiga tidak sama kaki
h
1
.
36
1 3
h
b
Ix =
b1 b2
)
.
(
.
36
1 2
2
2
2
b
b
b
b
h
b
Iy +
−
=
b
Bahan Ajar ‐ Mekanika Bahan ‐ Mulyati, MT

11. e. Lingkaran
r 1
r
r
4
64
1
d
I
I y
x π
=
=
D
f. Setengah lingkaran
r 4
8
1
r
I
I y
x π
=
=
D
Bahan Ajar ‐ Mekanika Bahan ‐ Mulyati, MT

12. y
yG
x1
xG
da
y1
M i i t l t h d b b d i titik b t
x
Suatu elemen da
• Momen inersia suatu elemen terhadap sumbu yang bergeser dari titik berat,
maka momen inersia terhadap sumbu x dan sumbu y adalah :
2
y
A
I
I +
=
2
1
1
.
.
x
A
I
I
y
A
I
I
yG
y
xG
x
+
=
+
=
Bahan Ajar ‐ Mekanika Bahan ‐ Mulyati, MT

13. • Jari‐jari putaran, jika momen inersia luasan A terhadap sumbu x dinyatakan
dengan I maka jari jari putaran r dapat didefinisikan dengan :
dengan Ix, maka jari‐jari putaran rx dapat didefinisikan dengan :
I
r x
=
A
rx =
dan jika momen inersia luasan A terhadap sumbu y dinyatakan dengan Iy, maka
jari‐jari putaran ry adalah :
A
I
r
y
y =
Bahan Ajar ‐ Mekanika Bahan ‐ Mulyati, MT

14. Contoh Soal dan Pembahasan
Penyelesaian :
a Letak titik berat
a. Letak titik berat.
A
A
A
x
A
x
x
.
.
2
1
2
2
1
1
−
−
=
cm
x
x
x .
15
)
20
.
.
(
)
60
30
(
)
20
.
.
.(
15
)
60
30
.(
15
3
4
1
2
4
1
=
−
−
=
π
π
A
y
A
y
y
.
. 2
2
1
1 −
=
cm
x
y
A
A
y
89
,
27
)
20
(
)
60
30
(
)
20
.
.
.(
40
)
60
30
.(
30
3
1
2
4
1
2
1
=
−
=
−
π
x
y ,
)
20
.
.
(
)
60
30
( 3
4
1
− π
Bahan Ajar ‐ Mekanika Bahan ‐ Mulyati, MT

15. b. Momen inersia penampang.
b. Momen inersia penampang.
( ) ( )
2
3
1
2
3
1
2
1
'
' y
A
h
b
y
A
h
b
I
I
I
I x
x
x
+
+
=
−
=
( ) ( )
( ) ( )
4
2
)
2
4
1
4
64
1
2
3
12
1
2
2
2
2
12
1
1
1
1
1
12
1
33
536355
79
,
40
).
20
.
.
(
20
.
.
89
,
27
).
60
30
(
60
.
30
.
.
.
.
.
.
.
I
x
I
y
A
h
b
y
A
h
b
I
x
x
+
−
+
=
+
−
+
=
π
π
4
.
33
,
536355 cm
Ix =
( ) ( )
2
2
2
2
3
2
12
1
2
1
1
1
3
1
12
1
2
1
'
.
.
.
'
.
.
. x
A
h
b
x
A
h
b
I
I
I
I
x
y
y
y
+
−
+
=
−
=
( ) ( )
4
2
)
2
4
1
4
64
1
2
3
12
1
.
02
,
127146
0
).
20
.
.
(
20
.
.
).
60
30
(
60
.
30
.
cm
I
o
x
I
x
x
=
+
−
+
= π
π
,
x
Bahan Ajar ‐ Mekanika Bahan ‐ Mulyati, MT