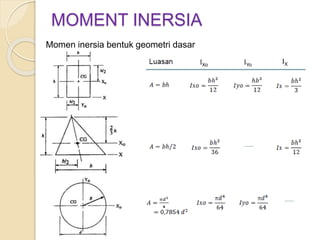
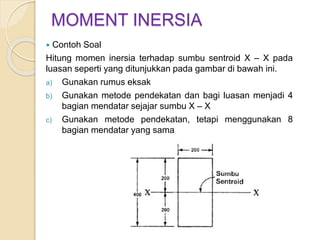
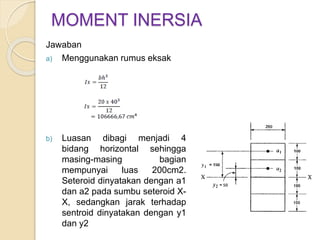
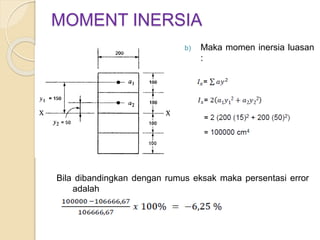
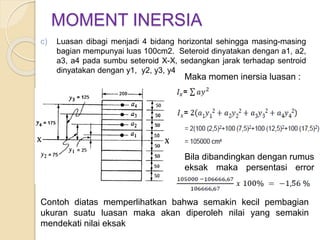
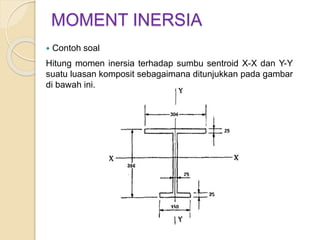
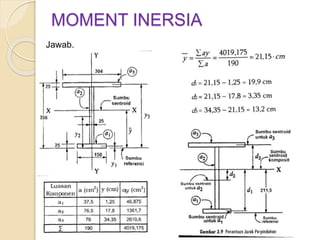
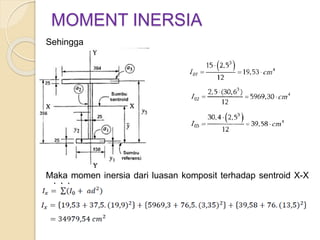
Dokumen ini menjelaskan mengenai momen inersia, yaitu ukuran inersia rotasi suatu benda yang dihitung terhadap sumbu tertentu. Momen inersia dinyatakan dalam satuan mm4 atau m4 dan selalu bernilai positif, serta dijelaskan melalui beberapa contoh soal yang melibatkan perhitungan momen inersia untuk bentuk geometri dasar dan luasan komposit. Beberapa metode pendekatan juga digunakan untuk mendapatkan nilai momen inersia yang mendekati nilai eksak.