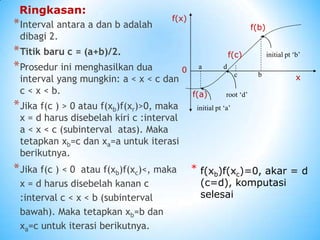
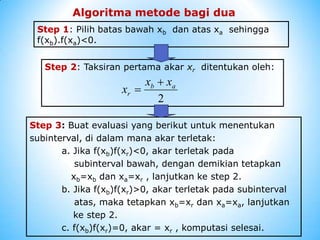
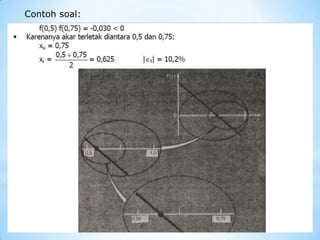
Metode numerik untuk menentukan akar fungsi terbagi menjadi tiga yaitu metode grafik, metode tertutup, dan metode terbuka. Metode tertutup meliputi metode bagi dua dan metode posisi palsu yang mencari akar dengan membagi interval secara iteratif. Metode terbuka meliputi metode Newton-Raphson dan metode secant yang menggunakan garis segitiga untuk memperkirakan akar berikutnya.

1. Mencari akar persamaan Non-Linear
Kuliah 2
METODE AKAR PERSAMAAN

2. Mechanical Engineering
Mencari nilai stiffness k dari suatu vibrating
mechanical system dimana displacement x(t)
menjadi nol pada t= 0.5sec. Displacement awal
adalah x0 dan velocity awal adalah nol. Mass m
dan damping c adalah diketahui, dan λ = c/(2m).
   
  

 
 

 
- t
0
x(t) = x e cos t + sin t = 0
dimana
2
2
k c
μ= -
m 4m

3. Akar Fungsi
Akar fungsi dapat didefinisikan dengan suatu
akar dari fungsi yang membuat persamaan itu
sama dengan nol.
f(a)=0 f(b)=0
a,b are roots of the
function f(x)
 Tujuannya
adalah
menyelesaikan
f(x) = 0, untuk
suatu fungsi
f(x).
 Nilai x dimana
membuat f(x) =
0 adalah akar
suatu
persamaan.

4. Akar Fungsi
 Aplikasi akar fungsi untuk bidang keteknikan
p = pressure,
T = temperature,
R = universal gas constant,
a & b = empirical constants
Chemical Engineering:
van der Waals equation; v = V/n (= volume/#
moles)
Mencari molal volume v :
2
a
f(v) = (p + )(v -b)- RT = 0
v

5. Civil Engineering :
Mencari horizontal component of tension, H,
dalam suatu kabel yang melalui (0,y0) and (x,y)
w = weight per unit length of cable
 
 
 
 
 
 
0
H wx
f(H) = cosh -1 + y - y = 0
w H

6. L = inductance,
C = capacitance,
q0 = initial charge
Electrical Engineering
Mencari resistance, R, dari suatu sirkuit yang
nilai arusnya mendekati nilai q pada waktu t
t
 
 
 
 
 
 
 
 
 
 
 
2
-Rt 2L
0
1 R q
f(R) = e cos - - = 0
LC 2L q

7. Akar Fungsi
Tinjau suatu fungsi kuadrat sebagai berikut:
0
)
(
0
)
( 2





 x
f
c
bx
ax
x
f
a
ac
b
b
x
2
4
2
2
,
1




Akar dari fungsi (persamaan) di atas adalah x1 dan x2
yang dapat ditentukan dengan persamaan di bawah ini:
Solusi eksak
?
0
4
log
sin
3 


 x
x
x
ex
Bagaimana dengan persamaan fungsi di bawah ini:

8. *
Secara umum, metode numerik untuk
menentukan akar fungsi terbagi tiga, yaitu:
1. Metode grafik
2. Metode tertutup
a. Metode bagi dua
b. Metode posisi palsu
3. Metode terbuka
a. Metode newton-raphson
b. Metode secant

9. *
x
e
x
f x

 
)
(
X 0 0,2 0,4 0,6 0,8 1,0
f(x) 1,0 0,61873 0,27032 -0,05119 -0,35067 -0,63212
Tinjau sebuah fungsi transenden di bawah ini:
Solusi:
Langkah 1: tentukan nilai f(x) untuk beberapa nilai x

10. Langkah 2: Plot harga-farga fungsi f(x) pada langkah 1
dalam bentuk sebuah grafik salib sumbu, sbb:
f(x)
x

11. Langkah 3: Lukis kurva melalui titik-titik data yang
diplot seperti pada gambar sebagai berikut:
Langkah 4: Estimasi dari gambar di atas diperoleh
bahwa akar berada pada interval x=0,5 dan x=0,6
f(x)
x
xr = estimasi akar
[perpotongan di f(x) =0]

12. Catatan:Jumlah akar yang terdapat pada interval [xb,xa]
tergantung pada bentuk fungsi (dimana xb adalah batas
interval bawah dan xa batas interval atas)
Jika f(xb).f(xa)>0
f(x)
x
xb xa
Tidak ada akar pada
interval [xb,xa]
f(x)
x
xb xa
Ada dua akar pada
interval [xb,xa]

13. Jika f(xb).f(xa)<0
f(x)
x
xb
xa
f(x)
x
xb
xa
Ada satu akar pada
interval [xb,xa]
Ada tiga akar pada
interval [xb,xa]
Simpulan:
1. Jika f(xb).f(xa)<0, maka akar dengan jumlah ganjil
dalam interval [xb,xa].
2. Jika f(xb).f(xa)>0, maka akar dengan jumlah genap
dalam interval [xb,xa].

14. *
Definisi: Yaitu suatu jenis pencarian
inkremental dimana interval senantiasa dibagi
separuhnya. Kalau suatu fungsi berubah tanda
sepanjang suatu interval, harga fungsi di
tengahnya dievaluasi. Letak akarnya kemudian
ditentukan ada di tengah-tengah subinterval
dimana perubahan tanda terjadi. Proses ini
diulangi untuk memperoleh taksiran yang
diperhalus.

15. *Ini metode sederhana
mencari akar fungsi.
*Membutuhkan dua
tebakan awal, a and b,
sehingga f(a) dan f(b)
mempunyai tanda
berlawanan.
initial pt ‘a’
root ‘d’
initial pt ‘b’
a
c b
d
f(a)
f(b)

16. *Pada metode ini (lihat
gambar) f(a) < 0 and f(b)
> 0.
*Akar d terletak antara a
and b!
initial pt ‘a’
root ‘d’
initial pt ‘b’
a
c b
d
f(a)
f(b)

17. *Akar d harus selalu di
antara a dan b
(bracketed)!
*Dilakukan iterasi untuk
mencari error yang
terkecil.
initial pt ‘a’
root ‘d’
initial pt ‘b’
a
c b
d
f(a)
f(b)

18. *Interval antara a dan b adalah
dibagi 2.
*Titik baru c = (a+b)/2.
*Prosedur ini menghasilkan dua
interval yang mungkin: a < x < c dan
c < x < b.
*Jika f(c ) > 0 atau f(xb)f(xr)>0, maka
x = d harus disebelah kiri c :interval
a < x < c (subinterval atas). Maka
tetapkan xb=c dan xa=a untuk iterasi
berikutnya.
*Jika f(c ) < 0 atau f(xb)f(xc)<, maka
x = d harus disebelah kanan c
:interval c < x < b (subinterval
bawah). Maka tetapkan xb=b dan
xa=c untuk iterasi berikutnya.
Ringkasan:
initial pt ‘a’
root ‘d’
initial pt ‘b’
a
c b
d
f(a)
f(b)
f(c)
0
f(x)
x
⃰ f(xb)f(xc)=0, akar = d
(c=d), komputasi
selesai

19. Step 1: Pilih batas bawah xb dan atas xa sehingga
f(xb).f(xa)<0.
Step 2: Taksiran pertama akar xr ditentukan oleh:
Step 3: Buat evaluasi yang berikut untuk menentukan
subinterval, di dalam mana akar terletak:
a. Jika f(xb)f(xr)<0, akar terletak pada
subinterval bawah, dengan demikian tetapkan
xb=xb dan xa=xr , lanjutkan ke step 2.
b. Jika f(xb)f(xr)>0, akar terletak pada subinterval
atas, maka tetapkan xb=xr dan xa=xa, lanjutkan
ke step 2.
c. f(xb)f(xr)=0, akar = xr , komputasi selesai.
2
a
b
r
x
x
x


Algoritma metode bagi dua

20. Contoh soal:

21. Contoh soal:

22. Contoh soal:

23. *

24. *
Teknik ini mirip dengan metode bagi dua kecuali bahwa
iterasi berikutnya diambil sebagai garis intersepsi
antara pasangan x-nilai dan sumbu x daripada di titik
tengah.

25. *
 
   
u
l
u
l
u
u
r
x
f
x
f
x
x
x
f
x
x




)
(
*
xr
xu
xl
f(xl)
f(xu)
 Dari segitiga
sebangun, kita dapat
tuliskan persamaan
sbb:
 
 
 
   
u
r
u
r
l
r
l
r
x
x
x
f
x
f
x
x
x
f
x
f




 (
)
)
(
(
)

26. *
*Berikan dua tebakan awal xl dan xu dimana akar
terletak diantara tebakan awal,
*Ulangi
*Set
*Jika adalah berlawanan tanda terhadap
maka
*Set xu = xr
*Jika tidak Set xl = xr
*Akhiri Jika
*Sampai < nilai toleransi.
 
   
u
l
u
l
u
u
r
x
f
x
f
x
x
x
f
x
x



 *
 
r
x
f
 
r
x
f  
l
x
f

27. *
*Hitung salah satu akar dari persamaan pangkat tiga
berikut ini:
f(x)=x3+x2 – 3x – 3=0
Solusi:
Seperti pada contoh metode bagi dua yang lalu,
langkah pertama adalah menghitung nilai f(x) pada
interval antara dua titik, misalnya xl=1 dan xu=2
sehingga nilai fungsi pada kedua titik tersebut
berlawanan tanda.
Untuk xl=1, f(x=1)=-4
xu=2, f(x=2)=3

28. *Dengan menggunakan persamaan:
*Karena f(xr) bertanda sama dengan f(xl)
maka xl=xr=1,57142 dan xu=2. Selanjutnya
hitung kembali nilai xr :
 
57142
,
1
3
4
2
1
*
3
2 





r
x
 
   
u
l
u
l
u
u
r
x
f
x
f
x
x
x
f
x
x



 *
70540
,
1
3
36449
,
1
)
2
57142
,
1
(
3
2 





r
x
36449
,
1
3
)
57142
,
1
(
3
)
57142
,
1
(
)
57142
,
1
(
)
( 2
3






r
x
f
24784
,
0
3
)
70540
,
1
(
3
)
70540
,
1
(
)
70540
,
1
(
)
( 2
3






r
x
f

29. *
iterasi xl xu xr f(xr) f(xl) f(xu)
1 1 2 1,57142 -1,36449 -4 3
2 1,571
42
2 1,70540 -0,24784 -1,36449 3
3 1,705
40
2
4
5

30. *

31. *
*Sekali lagi tebakan awal adalah
dipilih.
*Metode ini tidak mengharuskan
bahwa akar (root) adalah
bracketed!
*Dalam metode ini, suatu garis
lurus digambar melalui titik-titik
untuk mendapatkan satu titik
baru yang dekat akar persamaan.
*Ini diulagi sampai akar sebenarnya
ditemukan.

32. *
*Pertama kita menebak dua titik
(x0,x1), dimana adalah diharapkan
titik-titik tersebut dekat dengan
akar (untuk inisialisasi mungkin
bisa menggunakan metode bagi
dua).
*Satu garis adalah kemudian
digambar melalui dua titik dan
kita mencari dimana garis itu
berpotongan pada sumbu X.

33. *
*Jika f(x) adalah benar-benar
linear, garis lurus akan
memotong sumbu X pada
akar.
*Bagaimanapun jika fungsi
itu non linear, perpotongan
garis lurus adalah bukan
pada akar tetapi dekat pada
akar.

34. *
*Dari segitiga sebangun,
kita dapat tuliskan
persamaan sbb:
 
 
 
   
1
0
1
0
1
2
1
x
f
x
f
x
x
x
f
x
x




1
x 0
x
2
x
 
1
x
f
 
0
x
f

35. *
*Selanjutnya cari nilai
akar, x2:
   
   
1
0
1
0
1
1
2
x
f
x
f
x
x
x
f
x
x




1
x 0
x
2
x
 
1
x
f
 
0
x
f

36. *
*Persamaan Iterasi dari
metode ini adalah:
   
   
n
n
n
n
n
n
n
x
f
x
f
x
x
x
f
x
x







1
1
1

37. *
*Berikan dua nilai tebakan awal x0, x1 yang dekat dengan
akar fungsi,
*Jika maka
*Tukar x0 dan x1.
*Ulangi
* Set
* Set x0 = x1
* Set x1 = x2
*Sampai < nilai toleransi.
   
1
0 x
f
x
f 
 
   
1
0
1
0
1
1
2 *
x
f
x
f
x
x
x
f
x
x




 
2
x
f

38. *
*Hitung salah satu akar dari persamaan pangkat tiga berikut
ini:
f(x)=x3+x2 – 3x – 3=0
Solusi:
Dihitung nilai f(x) pada interval antara dua titik, misalnya
x0=1 dan x1=2.
Untuk x0=1, f(x=1)=-4
x1=2, f(x=2)=3
Tidak perlu tukar x0 dan x1
   
1
0 x
f
x
f 

39. Dengan menggunakan persamaan:
Iterasi kedua
x0=x1=2, f(x0=2)=3
x1=x2=1,57142, f(x1=1,57142) = -1,36449
   
   
n
n
n
n
n
n
n
x
f
x
f
x
x
x
f
x
x







1
1
1
   
   
57142
,
1
3
)
4
(
)
2
1
(
3
2
1
0
1
0
1
1
2 









x
f
x
f
x
x
x
f
x
x
70540
,
1
)
36449
,
1
(
3
)
57142
,
1
2
(
36449
,
1
57142
,
1
2 






x
   
   
1
0
1
0
1
1
2
x
f
x
f
x
x
x
f
x
x




   
1
0 x
f
x
f 

40. *
iterasi x0 x1 x2 f(x0) f(x1) f(x2)
1 1,0 2,0 1,57142 -4,0 3,0 -1,36449
2 2,0 1,57142 1,70540 -3,0 -1,36449 -0,24784
3 1,57142 1,70540 1,73513 -1,36449 -0,24784 0,02920
4 1,70540 1,73513 1,73199 -024784 0,02920 -0,000575
5 1,73513 1,73199 1,73205

41. *
*Metode secant menpunyai convergence lebih baik dibandingkan
metode bagi dua atau bisection method
*Karena akar tidak bracketed, maka mungkin ada kasus patologis
di mana algoritma menyimpang dari akar (divergen).
*Mungkin salah jika fungsi bukan kontinue.

42. *

43. *
Metode Newton ini sangat bergantung pada matematika
kalkulus dan menggunakan pendekatan linier untuk
fungsi dengan mencari tangen terhadap suatu kurva.

44. *
*Membutuhkan satu tebakan
awal, x0, yang dekat pada akar
sebenarnya.
*Titik dimana garis singgung
terhadap suatu fungsi {f(x)}
menemukan sumbu x adalah
perkiraan akar fungsi
selanjutnya, x1.
*Prosedur ini diulang sampai nilai
fungsi x adalah cukup dekat
terhadap nilai nol.

45. *
*Persamaan metode Newton
ini dapat ditentukan secara
grafis!
*Dari gambar di samping, tan
Ө = ƒ'(x0) = ƒ(x0)/(x0 – x1)
*Sehingga, x1=x0 -ƒ(x0)/ƒ'(x0).

46. *
Persamaan umum metode
Newton ini adalah:
xn+1 = xn – f(xn)/ƒ'(xn)
Algoritma:
*Pilih nilai awal untuk x
*Ulangi
* x:= x – f(x)/ƒ'(x)
*Kembali nilai x

47. *
Hitung salah satu akar dari persamaan pangkat tiga berikut ini
dengan metode Newton:
f(x)=x3+x2 – 3x – 3=0
Solusi:
Turunan pertama dari persamaan tersebut di atas adalah:
f’(x)=3x2+2x-3
Dengan menggunakan persamaan
xn+1 = xn – f(xn)/ƒ'(xn)

48. Pada awal perhitungan ditentukan nilai xi sembarang
misalnya x1=1, sehingga:
f(x1=1) = (1)3 +(1)2 – 3(1) -3 =-4
f’(x1=1) = 3(1)2 + 2(1) – 3 = 2
x2 =1 – (-4/2) = 3
Langkah berikutnya ditetapkan x2 = 3, sehingga:
f(x2=3) = (3)3 +(3)2 – 3(3) -3 =24
f’(x2=3) = 3(3)2 + 2(3) – 3 = 30
X3 =3 – (24/30) = 2,2

49. *
iterasi xi Xi+1 f(xi) f(xi+1)
1 1,0 3,0 -4,0 24
2 3,0 2,2 24 5,883
3 2,2 1,83 5,888 0,987387
4 1,83 1,73778 0,987387 0,005442
5 1,73778 1,73207 0,005442 0,0001816

50. Contoh solusi akar fungsi dengan
komputasi komputer
Carilah solusi akar fungsi positip persamaan
polinomial berikut ini dengan metode Newton
Raphson dan komputasi persamaan tersebut
dengan program komputer MabLab.
f(x) = x2 - 5

51. Solusi
Langkah Pertama.
Plot kurva dari persamaan polinomial tersebut sehingga garisnya
melintasi sumbu X.
Gunakan perintah program Matblab untuk memplot kurva, dengan
listing program:
Misalnya interval sumbu X yang dipilih dalam rentang -4<x<4
Tulis dalam window editor program:
x=linspace(-4,4,100); artinya=diberi 100 nilai diantara -4 dan 4
y=x.^2-5;
plot(x,y);grid

52. -4 -3 -2 -1 0 1 2 3 4
-6
-4
-2
0
2
4
6
8
10
12
Hasil eksekusi program (Grafik)
Root

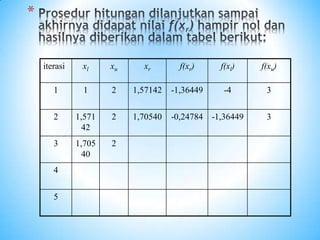
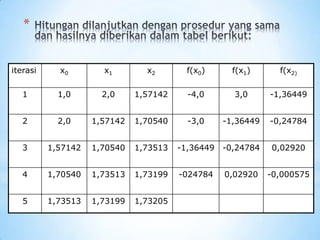
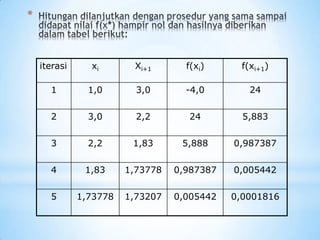
53. Diambil tebakan akar pertama (approximation)
adalah x0=2, maka:
x1 = x0 – f(x0)/ƒ'(x0) = 2 – [(2)2-5]/2(2) = 2.25
Aproksimasi kedua:
x2 = x1 – f(x1)/ƒ'(x1) = 2.25 – [(2.25)2-5]/2(2,25) = 2.2361
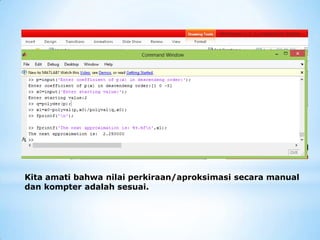
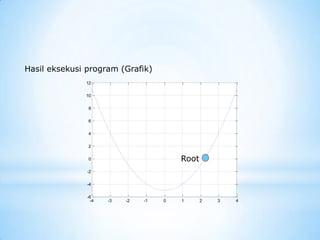
Solusi ini diverifikasi dengan program Matlab
Solusi manual

54. Script:
p=input('Enter coefficient of p(x) in descendeng order:');
Artinya: masukkan koefisien persamaan polinomial dalam bentuk
descendeng order.
x0=input('Enter starting value:');
Artinya: masukkan tebakan/aproksimasi pertama.
q=polyder(p);
Artinya: hitung turunan dari persamaan polinomial
x1=x0-polyval(p,x0)/polyval(q,x0);
Artinya: hitung nilai aproksimasi dengan metode Newton Raphson
fprintf('n');
Artinya: print blank area (spasi)
fprintf('The next approximation is: %9.6fn',x1);
Artinya: print nilai aproksimasi kedua dengan 9 digit dimana digit
6 adalah desimal
Solusi program matlab

55. Kita amati bahwa nilai perkiraan/aproksimasi secara manual
dan kompter adalah sesuai.