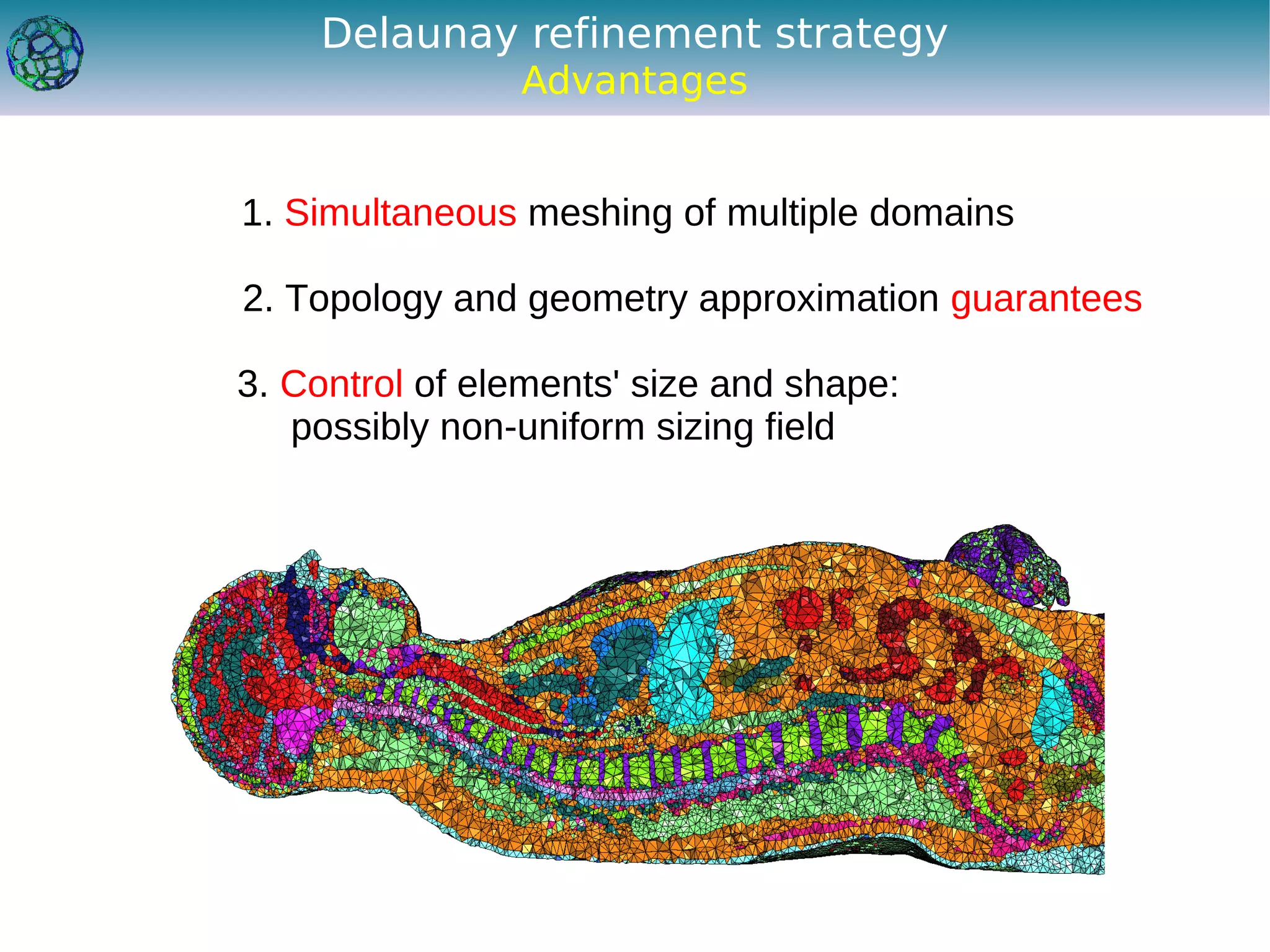
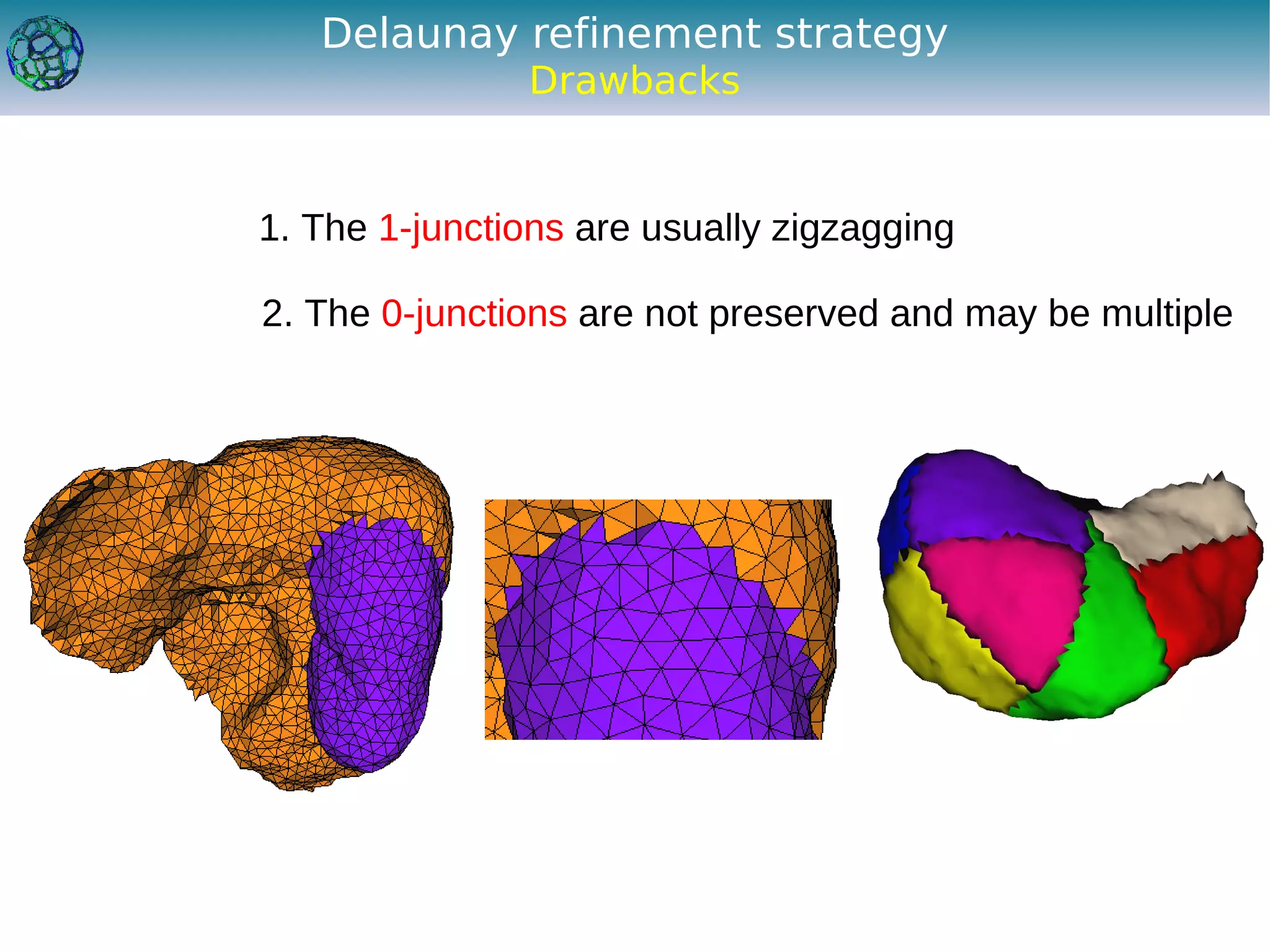
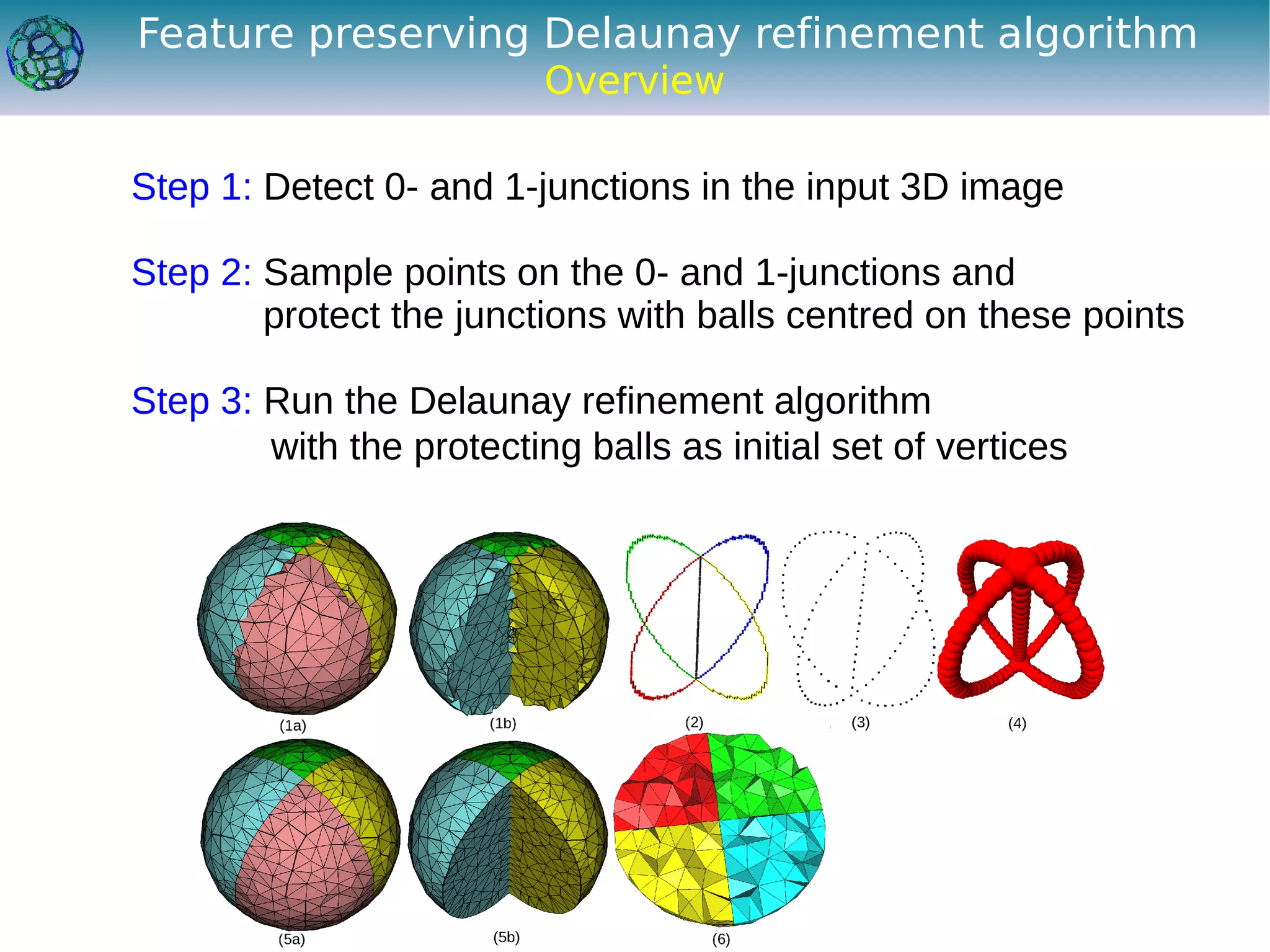
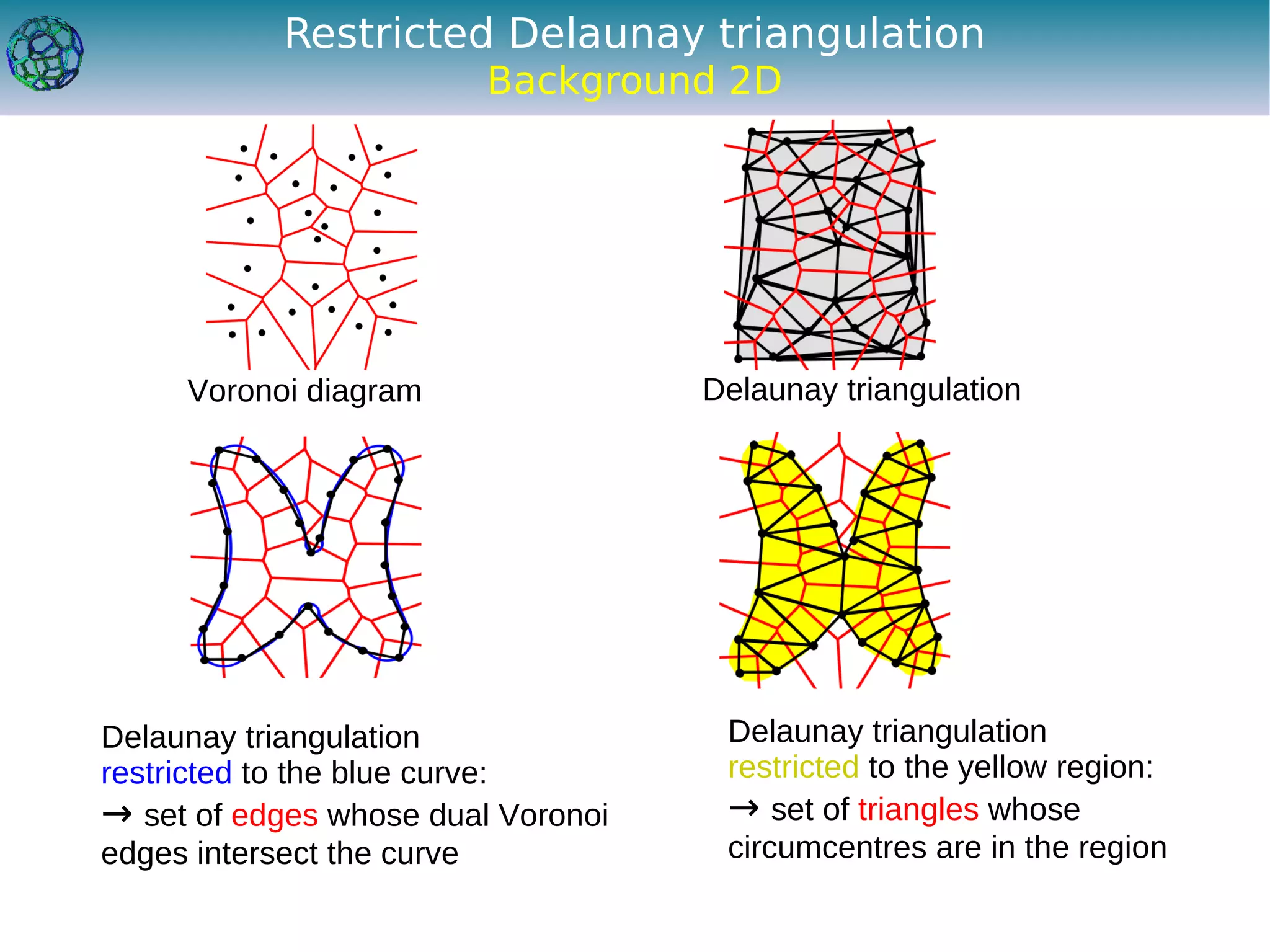
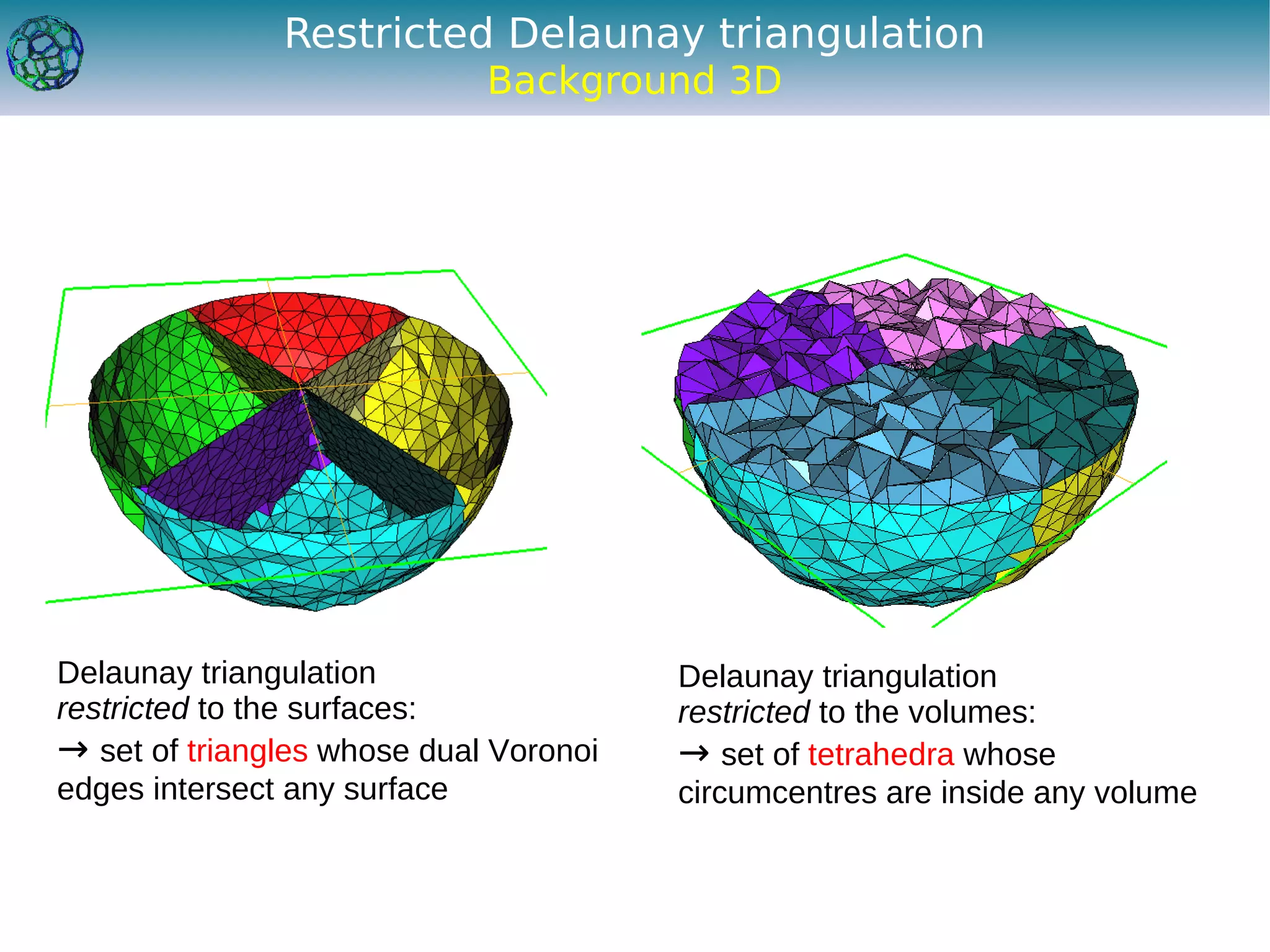
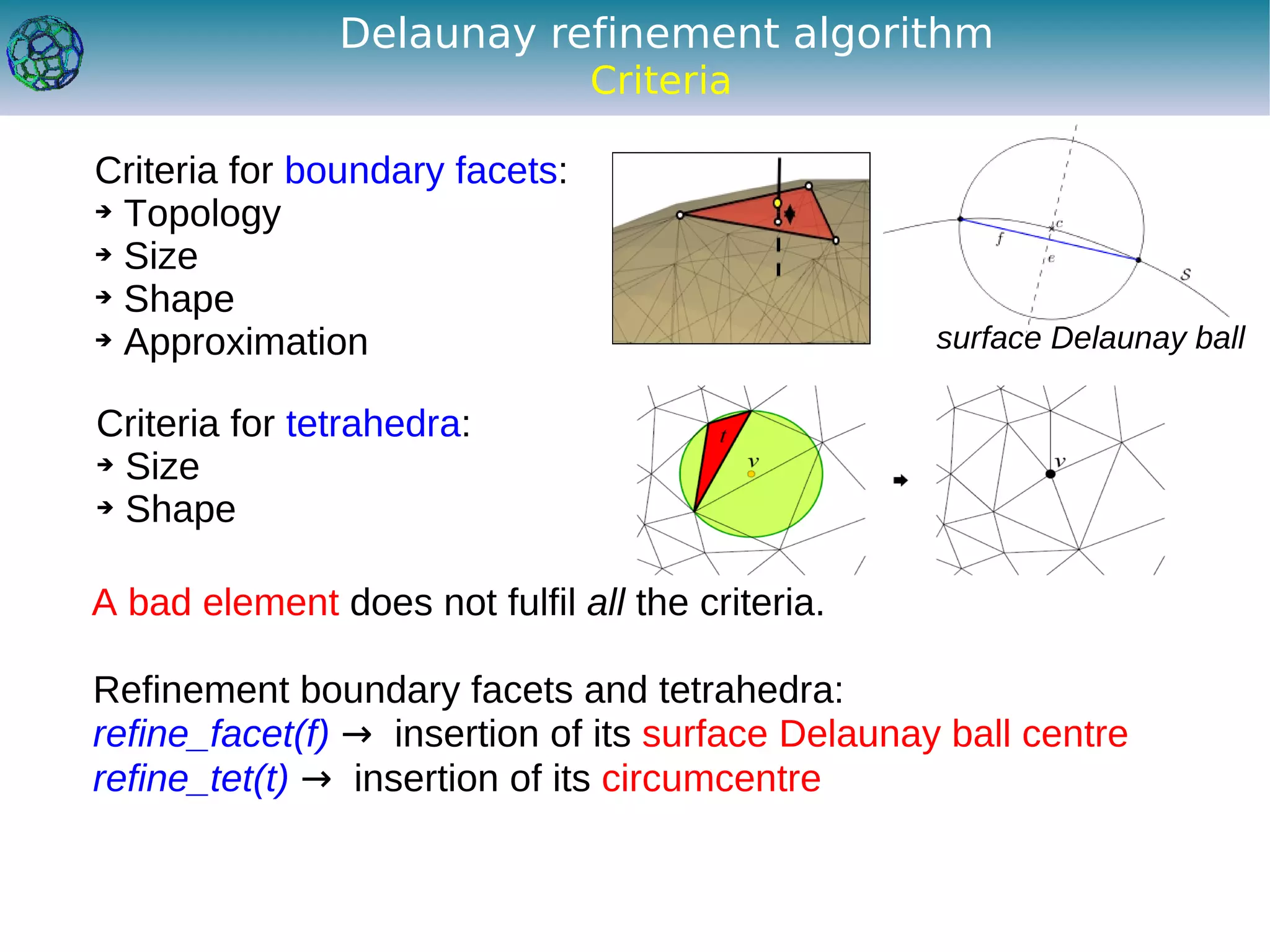
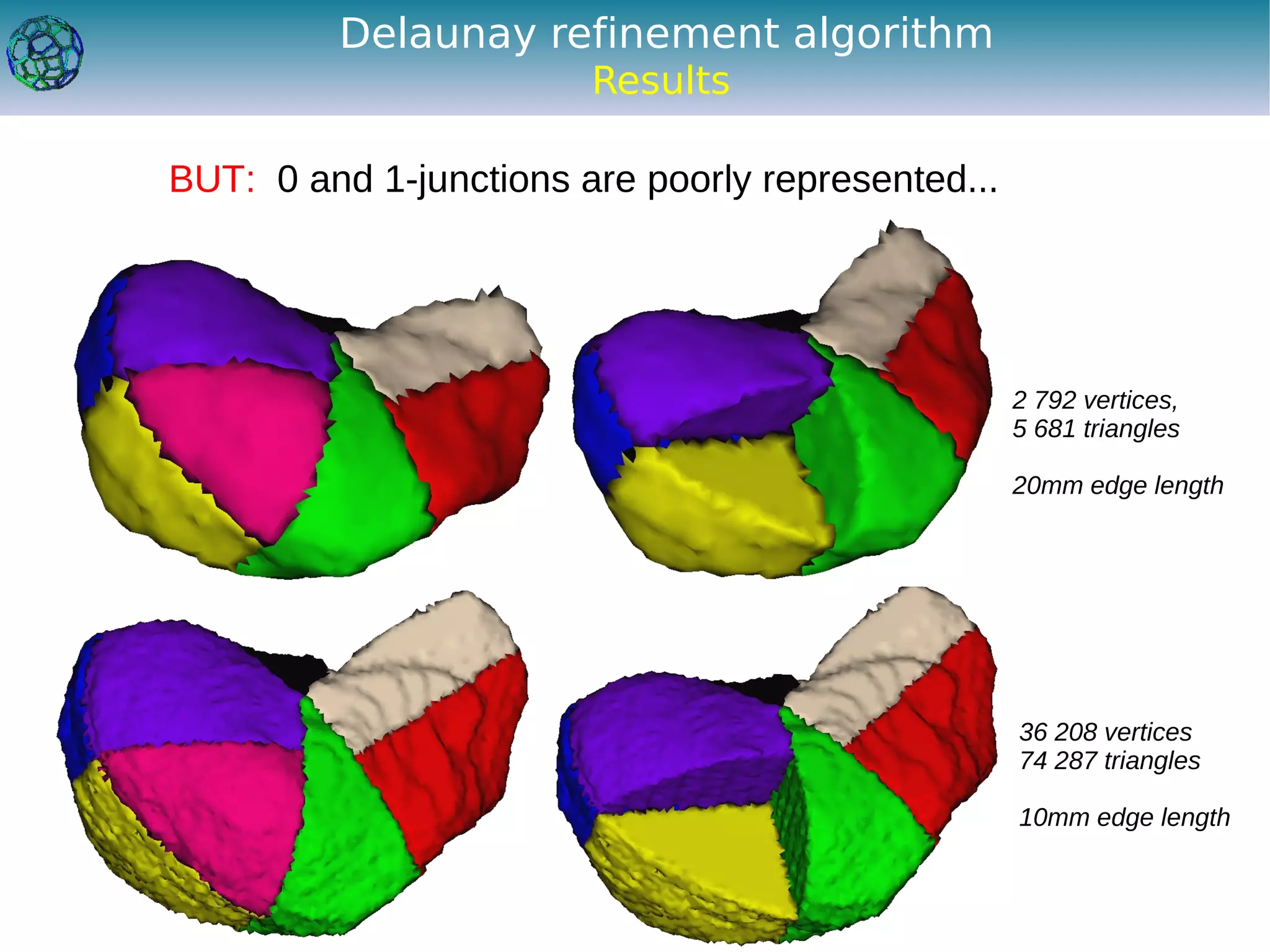
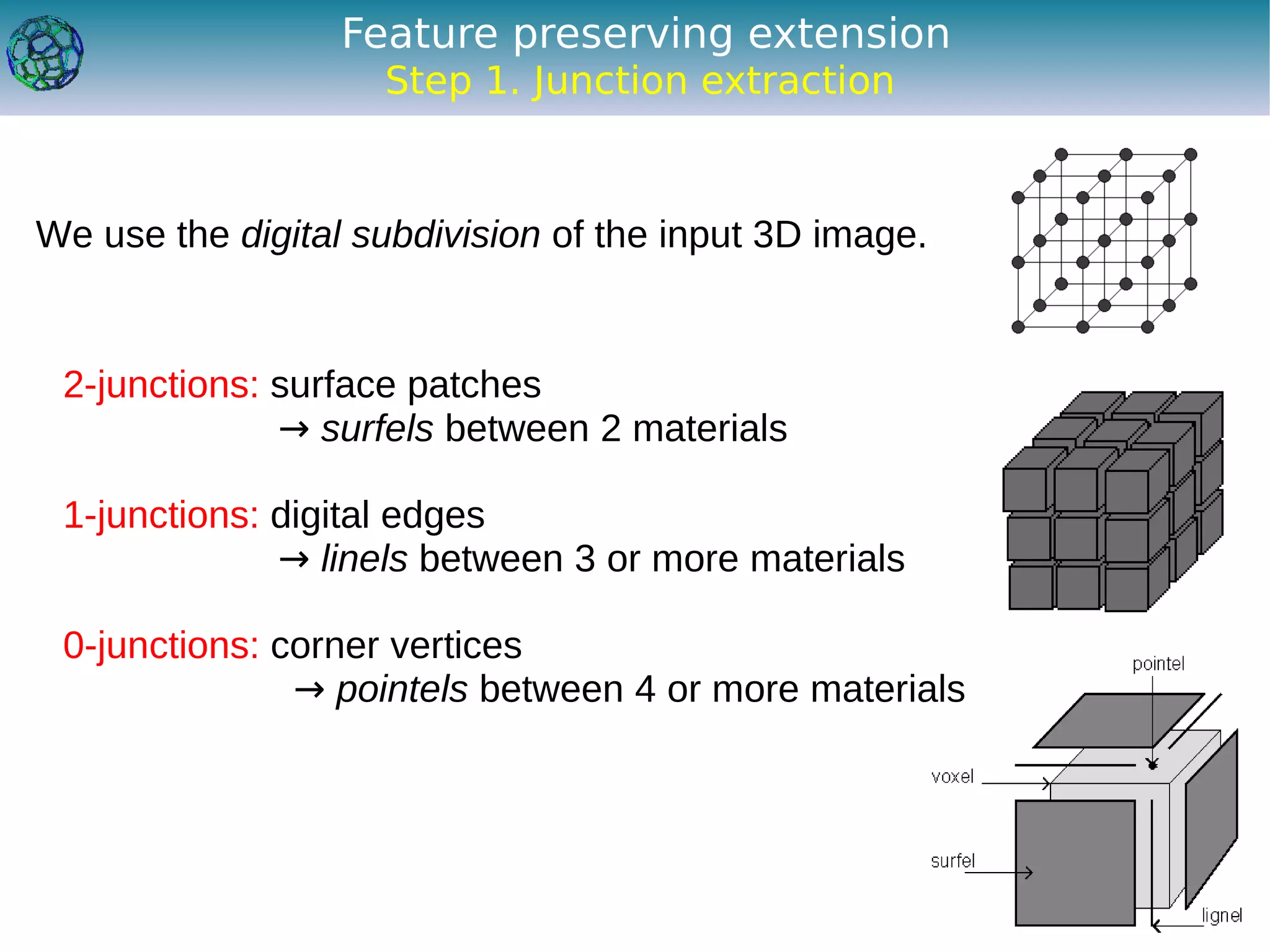
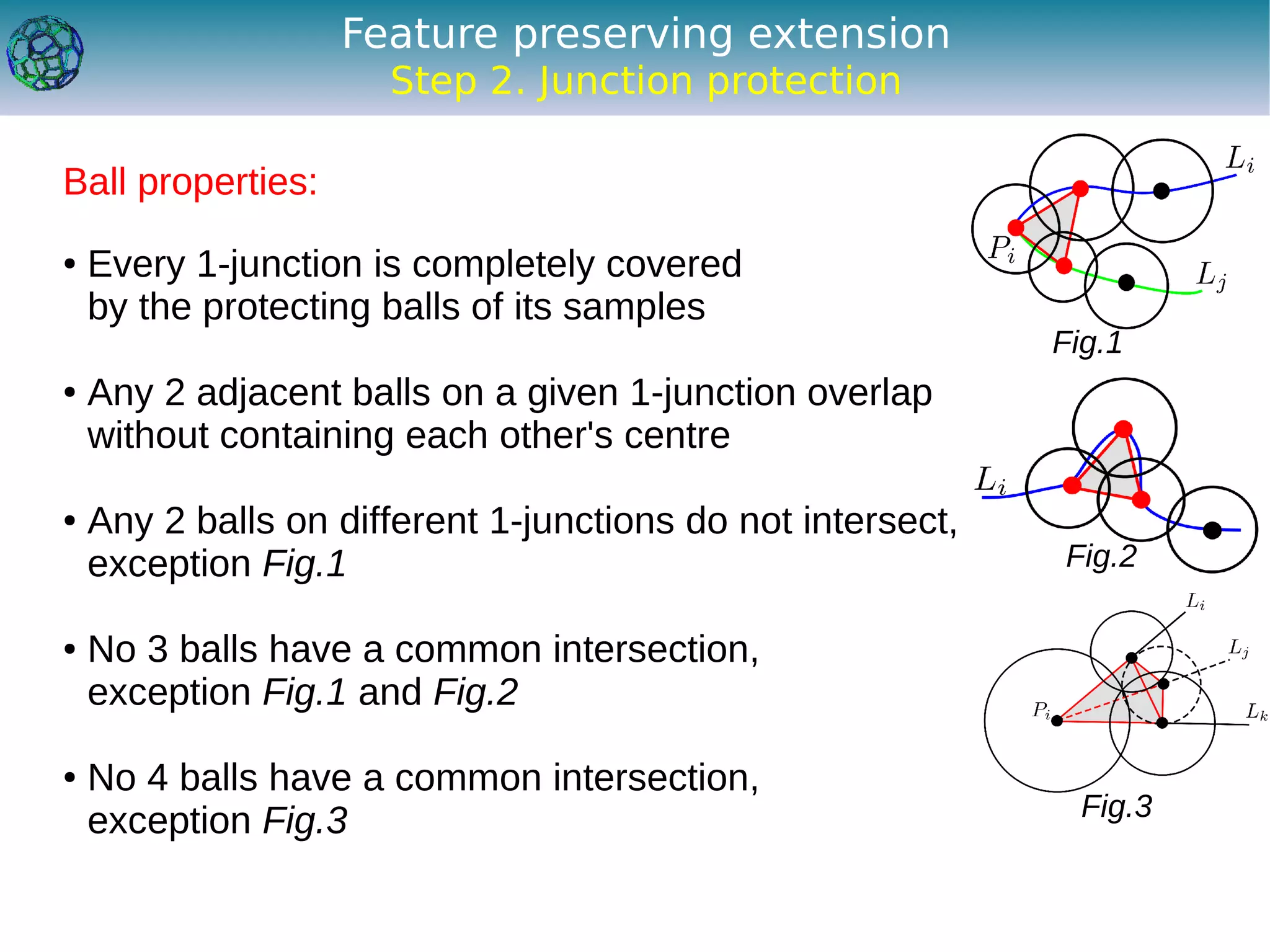
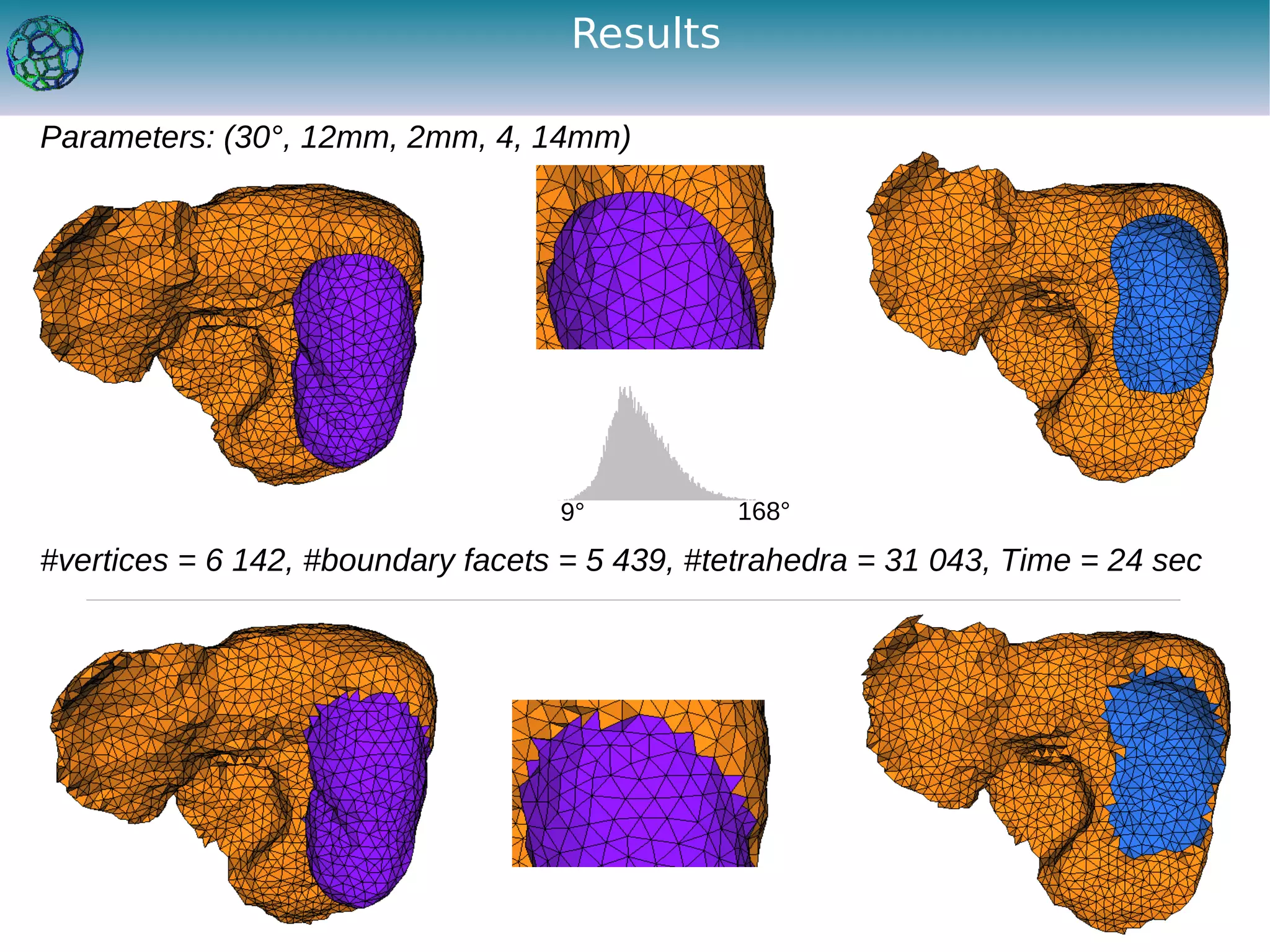
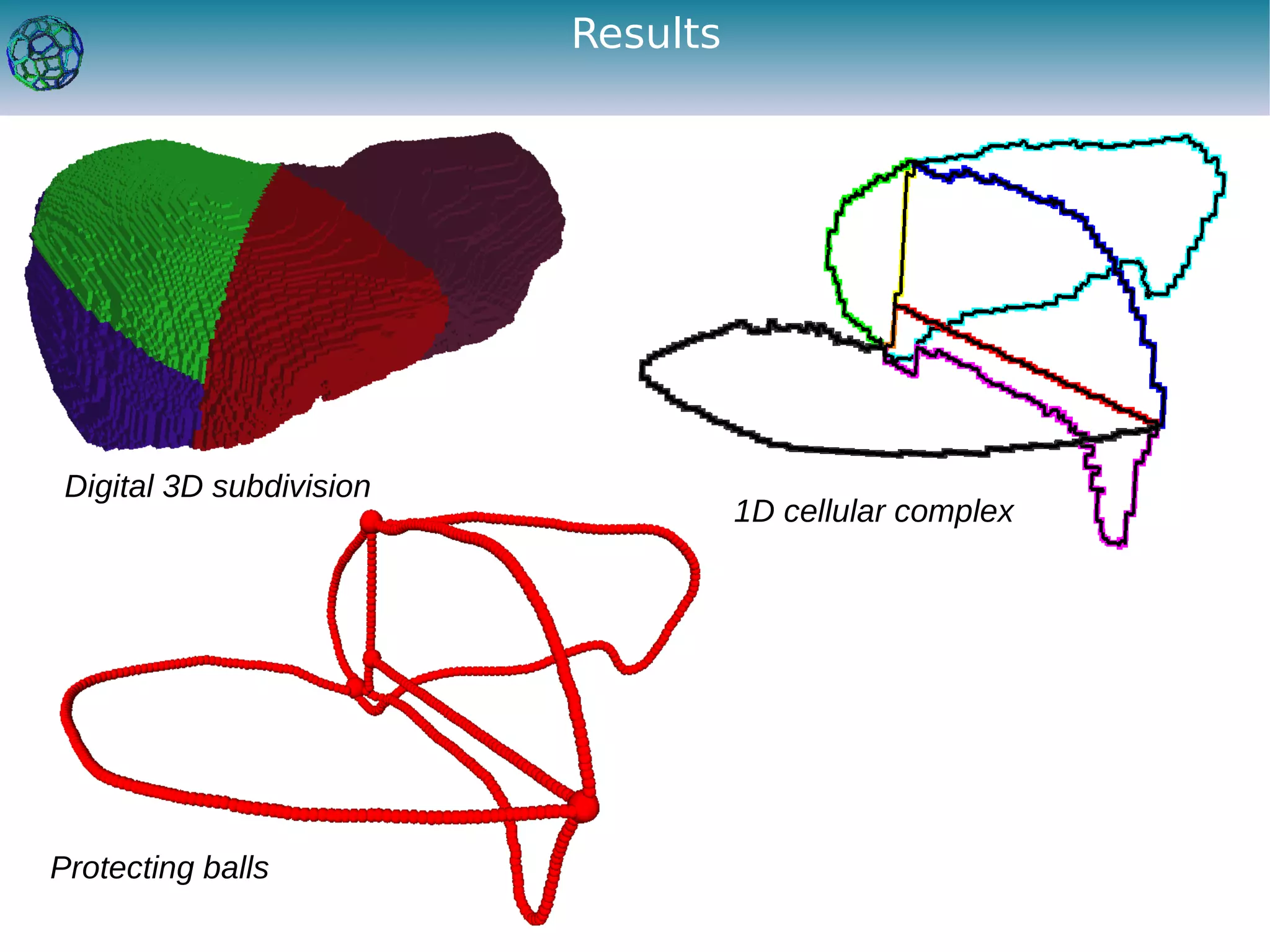
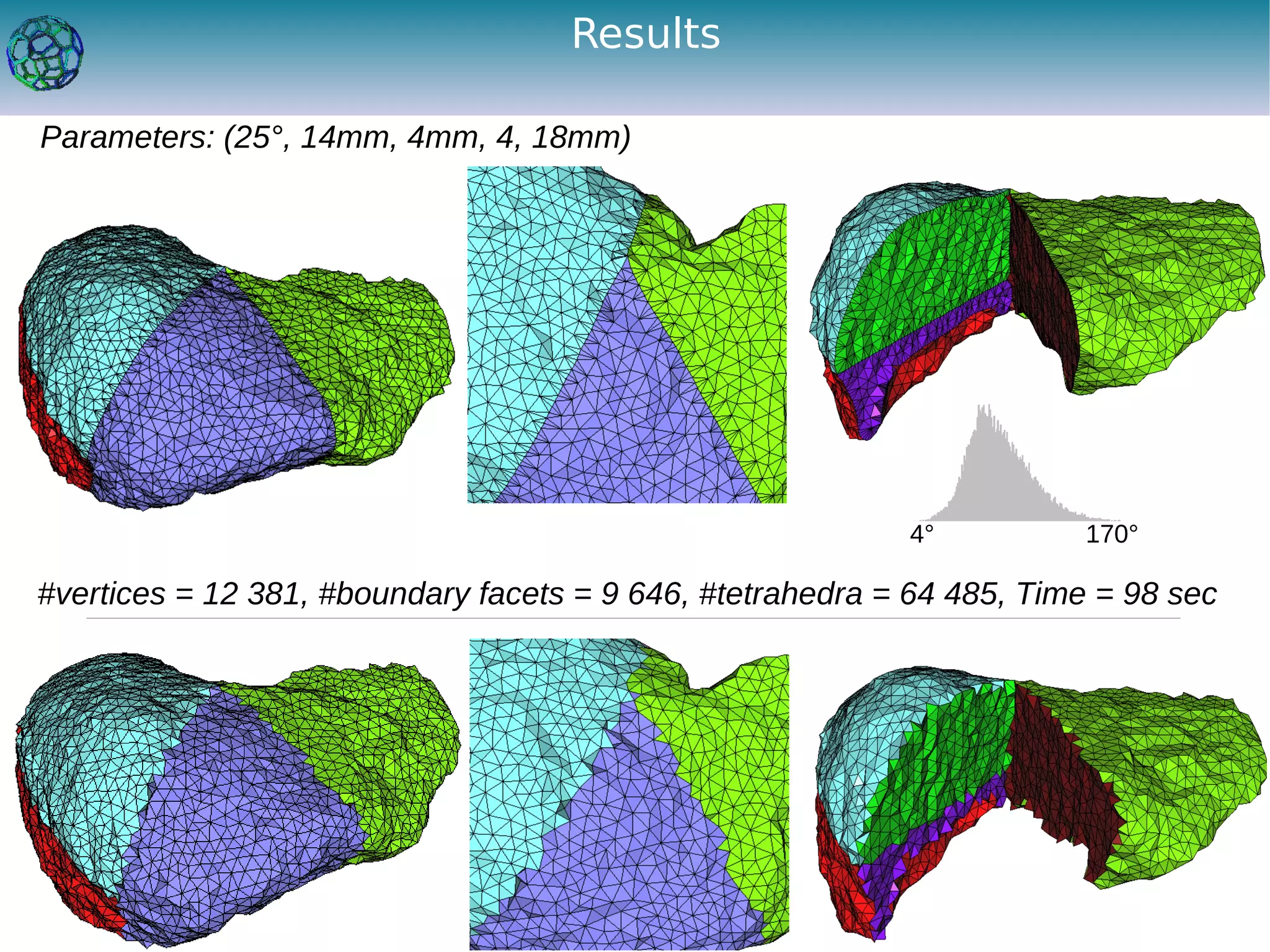
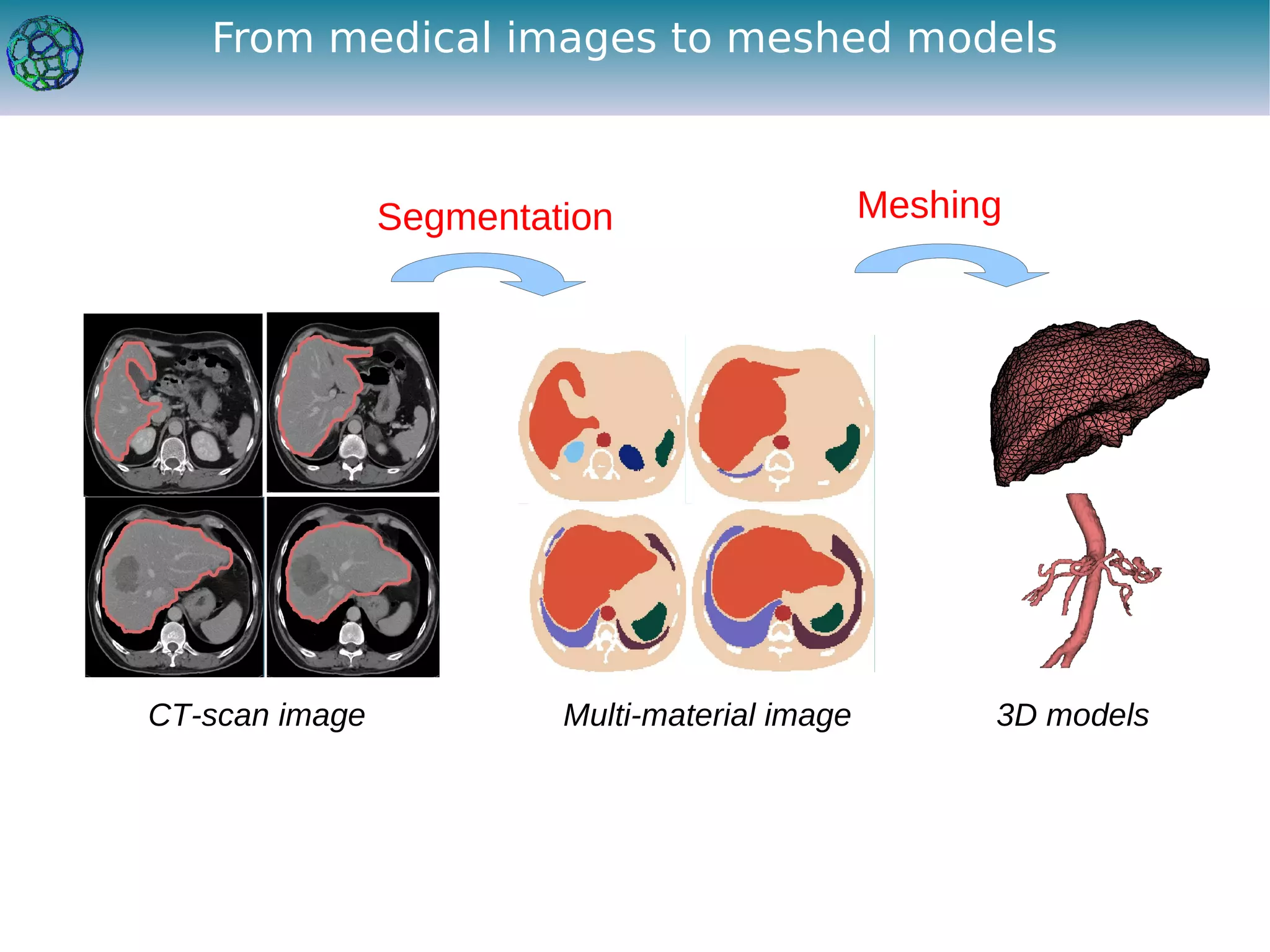
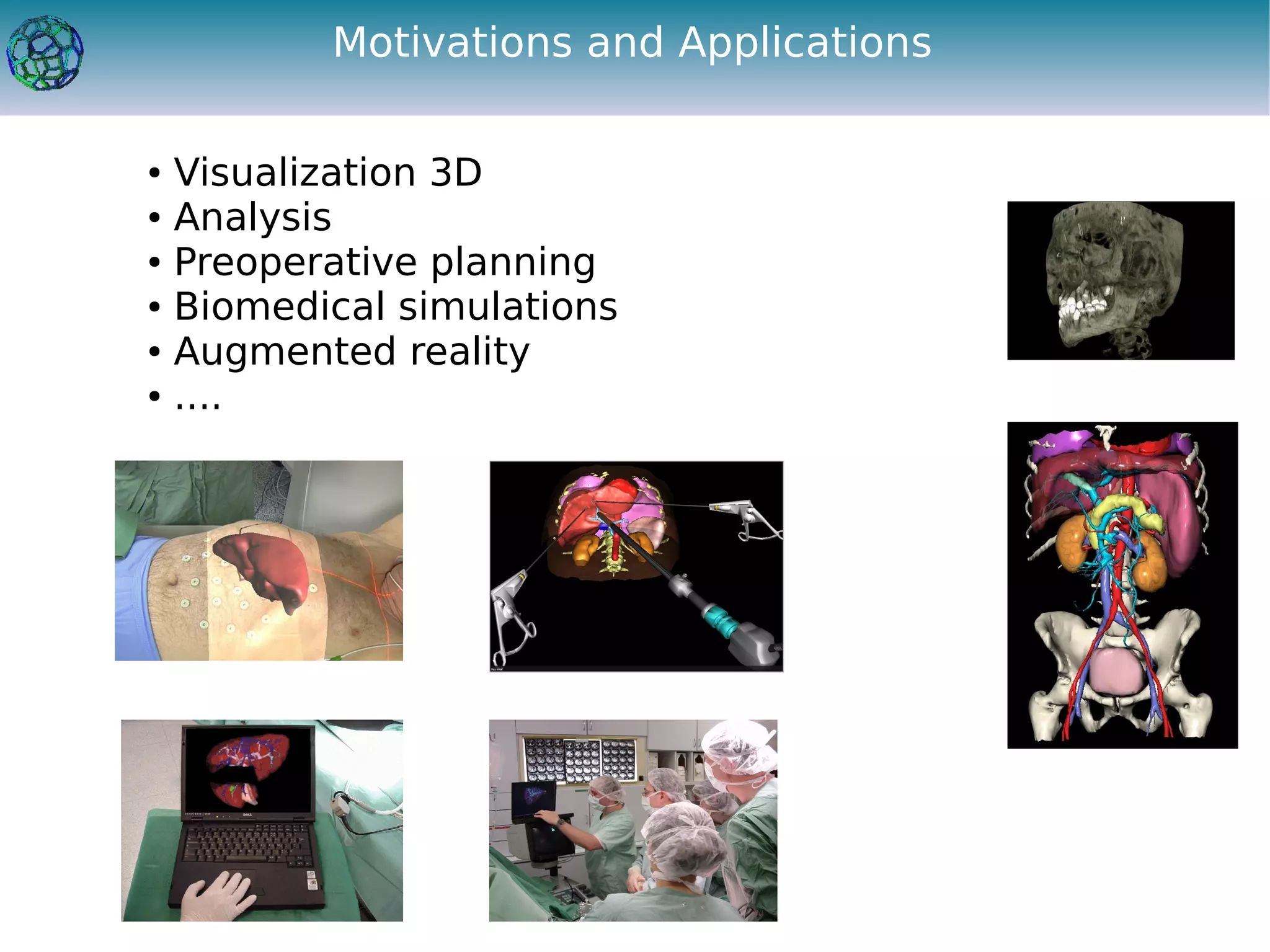
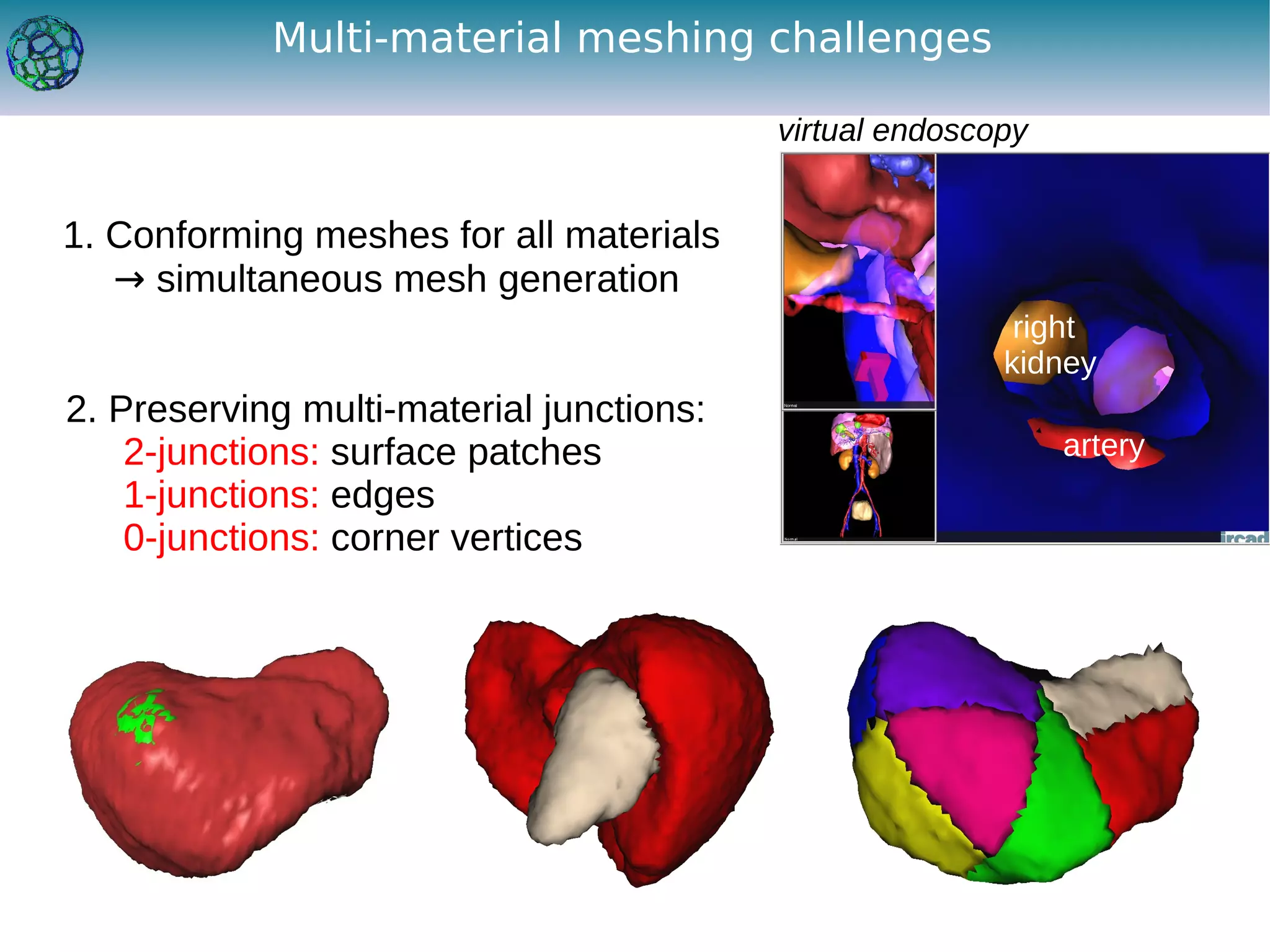
The document discusses the development of a feature-preserving Delaunay mesh generation technique from 3D multi-material images, aimed at improving medical visualization and analysis. It details the challenges of conforming meshes and preserving multi-material junctions, the Delaunay refinement algorithm applied in this context, and introduces a feature-preserving extension for better junction representation. Results show the algorithm effectively maintains mesh quality while representing different materials in the image, despite some limitations in junction representation.

1. Symposium on Geometry Processing
17th July 2009 - Berlin
Feature preserving
Delaunay mesh generation
from 3D multi-material images
Dobrina Boltcheva, Mariette Yvinec, Jean-Daniel Boissonnat

2. From medical images to meshed models
Segmentation Meshing
CT-scan image Multi-material image 3D models

3. Motivations and Applications
● Visualization 3D
● Analysis
● Preoperative planning
● Biomedical simulations
● Augmented reality
● ....

4. Multi-material meshing challenges
virtual endoscopy
1. Conforming meshes for all materials
→ simultaneous mesh generation
right
kidney
2. Preserving multi-material junctions:
2-junctions: surface patches artery
1-junctions: edges
0-junctions: corner vertices

5. Previous work
Surface mesh generation
 Marching Cubes extensions [Hege97,
Wu03, …]
 Dual Marching Cubes extensions [Gibson98, Nielson04,
Bertram05, Reitinger05, Kobbelt06…]
 Delaunay based methods [Amenta01, Boissonnat03, Meyer08…]

6. Previous work
Volume mesh generation
 Grid/Octree based methods [Nielson97, Hartman98, Bajaj07, …]
 Delaunay refinement based methods [Oudot05, Rineau06,
Yvinec07, Pons07…]

7. Delaunay refinement strategy
Advantages
1. Simultaneous meshing of multiple domains
2. Topology and geometry approximation guarantees
3. Control of elements' size and shape:
possibly non-uniform sizing field

8. Delaunay refinement strategy
Drawbacks
1. The 1-junctions are usually zigzagging
2. The 0-junctions are not preserved and may be multiple

9. Feature preserving Delaunay refinement algorithm
Overview
Step 1: Detect 0- and 1-junctions in the input 3D image
Step 2: Sample points on the 0- and 1-junctions and
protect the junctions with balls centred on these points
Step 3: Run the Delaunay refinement algorithm
with the protecting balls as initial set of vertices

10. Restricted Delaunay triangulation
Background 2D
Voronoi diagram Delaunay triangulation
Delaunay triangulation Delaunay triangulation
restricted to the blue curve: restricted to the yellow region:
→ set of edges whose dual Voronoi → set of triangles whose
edges intersect the curve circumcentres are in the region

11. Restricted Delaunay triangulation
Background 3D
Delaunay triangulation Delaunay triangulation
restricted to the surfaces: restricted to the volumes:
→ set of triangles whose dual Voronoi → set of tetrahedra whose
edges intersect any surface circumcentres are inside any volume

12. Delaunay refinement algorithm
The basic
1. Initialization – at least 3 points per material
2. Refinement – inserting new vertices,
maintaining the Delaunay triangulation,
its restriction to volumes and boundary facets
until there is no bad element left

13. Delaunay refinement algorithm
Criteria
Criteria for boundary facets:
➔ Topology
➔ Size
➔ Shape
➔ Approximation surface Delaunay ball
Criteria for tetrahedra:
➔ Size
➔ Shape
A bad element does not fulfil all the criteria.
Refinement boundary facets and tetrahedra:
refine_facet(f) → insertion of its surface Delaunay ball centre
refine_tet(t) → insertion of its circumcentre

14. Delaunay refinement algorithm
The algorithm
1. Initialization – at least 3 points per material
2. Refinement
a) If there is a bad boundary facet f
then refine_facet(f)
b) If there is a bad tetrahedron t
- compute the circumcentre c
- if c is included in a surface Delaunay ball
of some boundary facet f
- then refine_facet(f)
- else refine_tet(t)
3. Sliver exudation

15. Delaunay refinement algorithm
Results
● The algorithm terminates
● If the resulting sampling is dense enough,
every image material is represented by
a submesh of tetrahedra
→ boundary facets provide a good and
watertight approximation of the surface,
free of self intersections
→ tetrahedra form a good approximation
of the volume

16. Delaunay refinement algorithm
Results
BUT: 0 and 1-junctions are poorly represented...
2 792 vertices,
5 681 triangles
20mm edge length
36 208 vertices
74 287 triangles
10mm edge length

17. Feature preserving extension
Step 1: Multi-material junction extraction
Step 2: Junction protection
Step 3: Adaptation of the algorithm

18. Feature preserving extension
Step 1. Junction extraction
We use the digital subdivision of the input 3D image.
2-junctions: surface patches
→ surfels between 2 materials
1-junctions: digital edges
→ linels between 3 or more materials
0-junctions: corner vertices
→ pointels between 4 or more materials

19. Feature preserving extension
Step 1. Junction extraction
Digital 3D subdivision 1D cellular complex:
Five 1-junctions and two 0-junctions

20. Feature preserving extension
Step 2. Junction protection
1. Sample all 0-junctions
2. Sample points on 1-junctions with
a user-given density d.
3. Cover junctions with
protecting balls b(p,r) with r=2/3*d
centred on sampled points

21. Feature preserving extension
Step 2. Junction protection
Ball properties:
● Every 1-junction is completely covered
by the protecting balls of its samples
Fig.1
● Any 2 adjacent balls on a given 1-junction overlap
without containing each other's centre
● Any 2 balls on different 1-junctions do not intersect,
exception Fig.1 Fig.2
● No 3 balls have a common intersection,
exception Fig.1 and Fig.2
● No 4 balls have a common intersection,
Fig.3
exception Fig.3

22. Feature preserving extension
Step 3. Algorithm adaptation
The algorithm is tuned to use a weighted Delaunay triangulation.
1. Initialization – with the weighted points corresponding
to the protecting balls
2. Refinement
a) If there is a bad boundary facet f
then refine_facet(f)
b) If there is a bad tetrahedron t
- compute the weighted circumcentre c
- if c is included in a weighted surface Delaunay ball
of some boundary facet f
- then refine_facet(f)
- else refine_tet(t)
3. Sliver exudation

23. Feature preserving extension
Step 3. Criteria adaptation
Boundary facet f with initial vertices whose protecting balls intersect
● 3 → f is never refined
● 2 or 1 → topology and sizing criteria
Tetrahedron t with initial vertices whose protecting balls intersect
● 4 → t is never refined
● 3 → sizing
(check surface Delaunay ball of the constrained facet)
● 2 or 1 → sizing

24. Feature preserving extension
Why does it work?
1. Refinement points inserted only outside the protecting balls:
→ meshing independent 2-junctions
2. Relaxed quality criteria in proximity to 0- and 1-junctions:
→ algorithm termination
Result: any 2 consecutive points on a 1-junction
remain connected with a restricted Delaunay edge
Note: the difference between digital and trilinear
junction definitions is hidden by
the protecting balls

25. Results
Parameters: (30°, 12mm, 2mm, 4, 14mm)
9° 168°
#vertices = 6 142, #boundary facets = 5 439, #tetrahedra = 31 043, Time = 24 sec

26. Results
Digital 3D subdivision
1D cellular complex
Protecting balls

27. Results
Parameters: (25°, 14mm, 4mm, 4, 18mm)
4° 170°
#vertices = 12 381, #boundary facets = 9 646, #tetrahedra = 64 485, Time = 98 sec

28. Acknowledgements
Thank you for your attention !