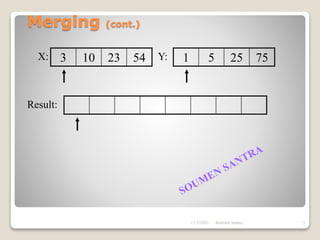
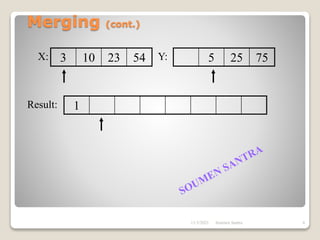
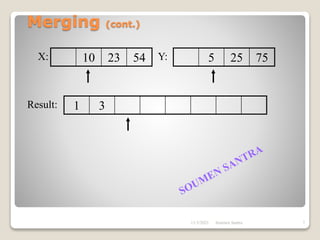
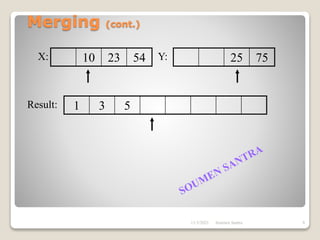
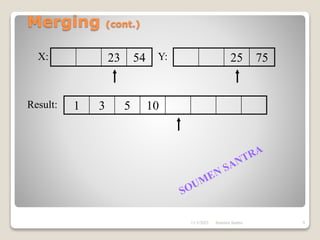
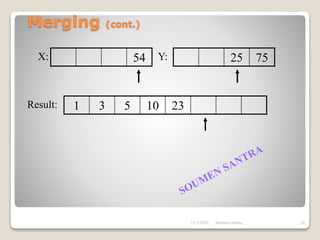
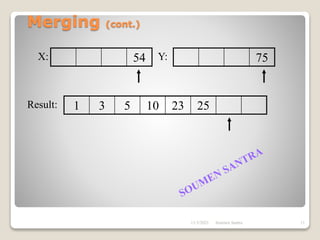
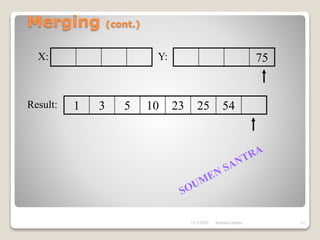
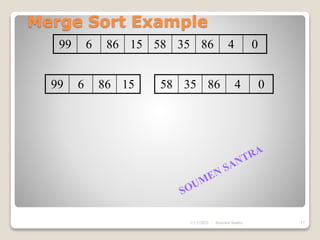
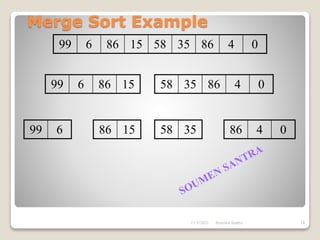
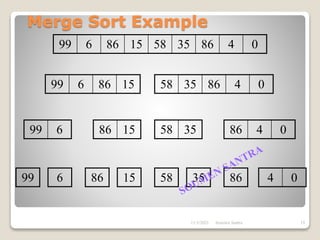
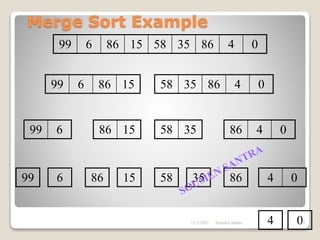
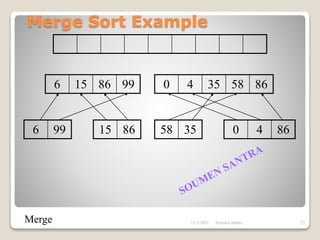
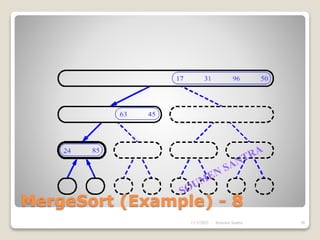
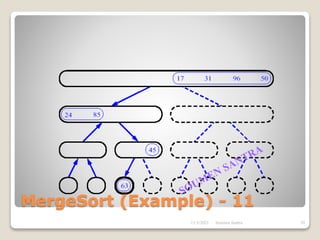
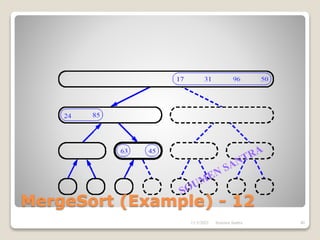
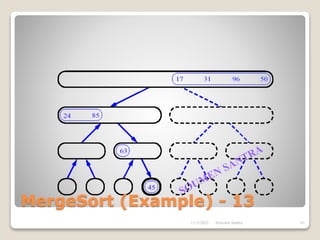
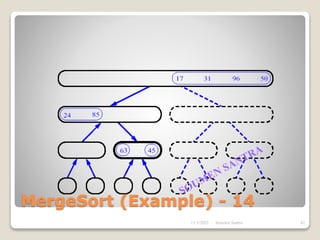
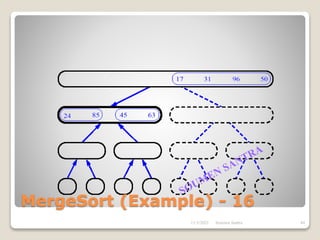
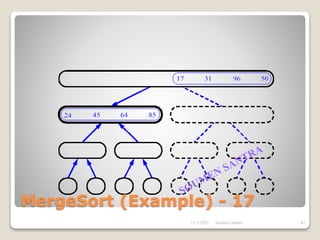
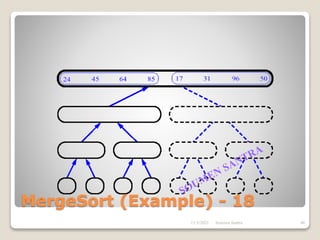
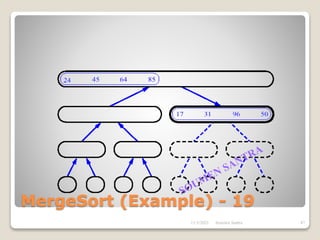
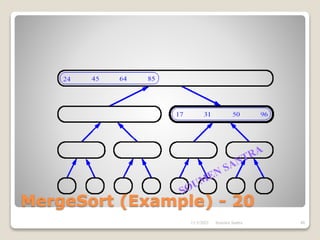
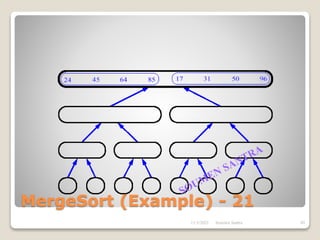
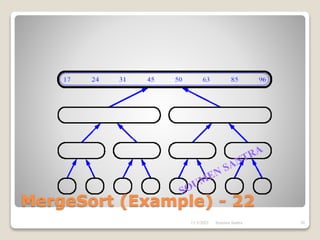
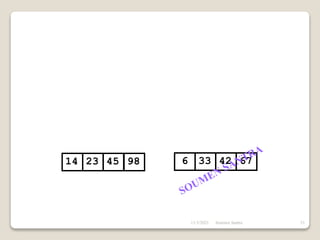
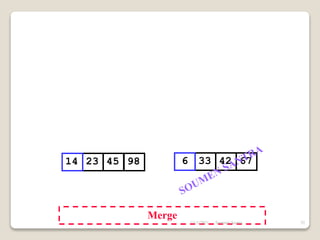
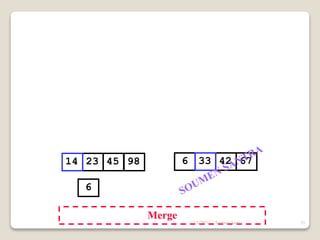
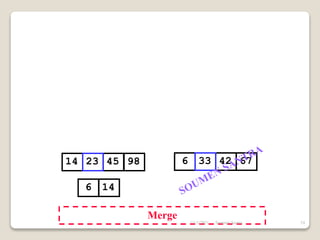
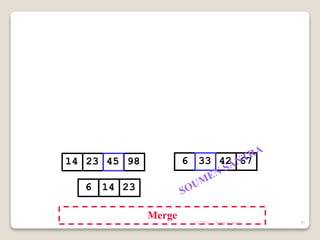
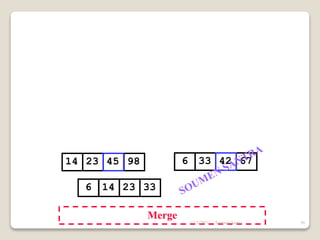
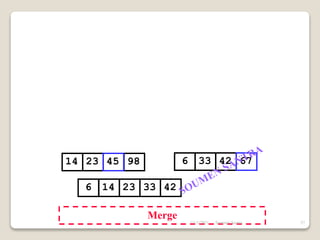
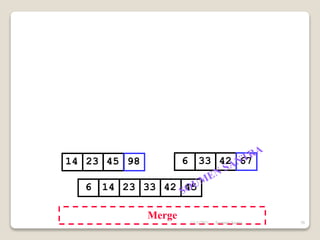
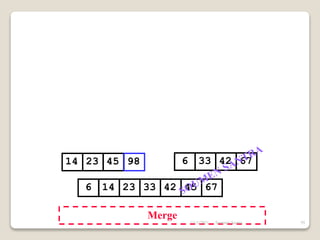
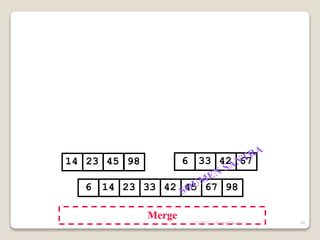
The presentation outlines the merge sort algorithm, developed by John von Neumann in 1945, which sorts data by recursively dividing lists and merging them. It describes the merging process, its implementation options, and highlights that while merge sort has a time complexity of O(n log n), its memory requirements can be impractical for large datasets. Different variants of merge sorts exist, but the double memory version is commonly discussed, though it can be less efficient due to memory consumption.

1. Merge Sort
Presentation By: Soumen Santra
TINT

2. In the Beginning…
John von Neumann
(1903-1957)
 Stored program
 Developed merge
sort for EDVAC in
1945
11/3/2021 2
Soumen Santra

3. Merging
 The key to Merge Sort is merging two
sorted lists into one, such that if you
have two lists X (x1x2…xm) and
Y(y1y2…yn) the resulting list is
Z(z1z2…zm+n)
 Example:
L1 = { 3 8 9 } L2 = { 1 5 7 }
merge(L1, L2) = { 1 3 5 7 8 9 }
11/3/2021 3
Soumen Santra

4. Merging (cont.)
 The merge
Algorithm:
From The Art of
Computer
Programming
vol2: Sorting and
Searching
by Donald E.
Knuth
(page 160).
11/3/2021 4
Soumen Santra

5. Merging (cont.)
3 10 23 54 1 5 25 75
X: Y:
Result:
11/3/2021 5
Soumen Santra

6. Merging (cont.)
3 10 23 54 5 25 75
1
X: Y:
Result:
11/3/2021 6
Soumen Santra

7. Merging (cont.)
10 23 54 5 25 75
1 3
X: Y:
Result:
11/3/2021 7
Soumen Santra

8. Merging (cont.)
10 23 54 25 75
1 3 5
X: Y:
Result:
11/3/2021 8
Soumen Santra

9. Merging (cont.)
23 54 25 75
1 3 5 10
X: Y:
Result:
11/3/2021 9
Soumen Santra

10. Merging (cont.)
54 25 75
1 3 5 10 23
X: Y:
Result:
11/3/2021 10
Soumen Santra

11. Merging (cont.)
54 75
1 3 5 10 23 25
X: Y:
Result:
11/3/2021 11
Soumen Santra

12. Merging (cont.)
75
1 3 5 10 23 25 54
X: Y:
Result:
11/3/2021 12
Soumen Santra

13. Merging (cont.)
1 3 5 10 23 25 54 75
X: Y:
Result:
11/3/2021 13
Soumen Santra

14. Divide And Conquer
 Merging a two lists of one element each is
the same as sorting them.
 Merge sort divides up an unsorted list until
the above condition is met and then sorts the
divided parts back together in pairs.
 Specifically this can be done by recursively
dividing the unsorted list in half, merge
sorting the right side then the left side and
then merging the right and left back
together.
11/3/2021 14
Soumen Santra

15. Merge Sort Algorithm
Given a list L with a length k:
 If k == 1  the list is sorted
 Else:
◦ Merge Sort the left side (0 thru k/2)
◦ Merge Sort the right side (k/2+1 thru k)
◦ Merge the right side with the left side
11/3/2021 15
Soumen Santra

16. Merge Sort Example
99 6 86 15 58 35 86 4 0
11/3/2021 16
Soumen Santra

17. Merge Sort Example
99 6 86 15 58 35 86 4 0
99 6 86 15 58 35 86 4 0
11/3/2021 17
Soumen Santra

18. Merge Sort Example
99 6 86 15 58 35 86 4 0
99 6 86 15 58 35 86 4 0
86 15
99 6 58 35 86 4 0
11/3/2021 18
Soumen Santra

19. Merge Sort Example
99 6 86 15 58 35 86 4 0
99 6 86 15 58 35 86 4 0
86 15
99 6 58 35 86 4 0
99 6 86 15 58 35 86 4 0
11/3/2021 19
Soumen Santra

20. Merge Sort Example
99 6 86 15 58 35 86 4 0
99 6 86 15 58 35 86 4 0
86 15
99 6 58 35 86 4 0
99 6 86 15 58 35 86 4 0
4 0
11/3/2021 20
Soumen Santra

21. Merge Sort Example
99 6 86 15 58 35 86 0 4
4 0
Merge 11/3/2021 21
Soumen Santra

22. Merge Sort Example
15 86
6 99 58 35 0 4 86
99 6 86 15 58 35 86 0 4
Merge 11/3/2021 22
Soumen Santra

23. Merge Sort Example
6 15 86 99 0 4 35 58 86
15 86
6 99 58 35 0 4 86
Merge 11/3/2021 23
Soumen Santra

24. Merge Sort Example
0 4 6 15 35 58 86 86 99
6 15 86 99 0 4 35 58 86
Merge 11/3/2021 24
Soumen Santra

25. Merge Sort Example
0 4 6 15 35 58 86 86 99
11/3/2021 25
Soumen Santra

26. Implementing Merge Sort
 There are two basic ways to implement
merge sort:
◦ In Place: Merging is done with only the input array
 Pro: Requires only the space needed to hold the array
 Con: Takes longer to merge because if the next element
is in the right side then all of the elements must be
moved down.
◦ Double Storage: Merging is done with a temporary
array of the same size as the input array.
 Pro: Faster than In Place since the temp array holds the
resulting array until both left and right sides are merged
into the temp array, then the temp array is appended
over the input array.
 Con: The memory requirement is doubled.
 The merge sort in the text (ch7.6:p238-239) is an
example of a double array implementation with
Comparable objects.
11/3/2021 26
Soumen Santra

27. Merge Sort Analysis
The Double Memory Merge Sort runs O (N log N) for
all cases, because of its Divide and Conquer approach.
T(N) = 2T(N/2) + N = O(N logN)
11/3/2021 27
Soumen Santra

28. Finally…
There are other variants of Merge Sorts including k-
way merge sorting, but the common variant is the Double
Memory Merge Sort. Though the running time is O(N logN)
and runs much faster than insertion sort and bubble sort,
merge sort’s large memory demands makes it not very
practical for main memory sorting.
Important things to remember for the Midterm:
• Best Case, Average Case, and Worst Case = O(N logN)
• Storage Requirement: Double that needed to hold the array
to be sorted.
11/3/2021 28
Soumen Santra

29. MergeSort (Example) - 1
11/3/2021 29
Soumen Santra

30. MergeSort (Example) - 2
11/3/2021 30
Soumen Santra

31. MergeSort (Example) - 3
11/3/2021 31
Soumen Santra

32. MergeSort (Example) - 4
11/3/2021 32
Soumen Santra

33. MergeSort (Example) - 5
11/3/2021 33
Soumen Santra

34. MergeSort (Example) - 6
11/3/2021 34
Soumen Santra

35. MergeSort (Example) - 7
11/3/2021 35
Soumen Santra

36. MergeSort (Example) - 8
11/3/2021 36
Soumen Santra

37. MergeSort (Example) - 9
11/3/2021 37
Soumen Santra

38. MergeSort (Example) - 10
11/3/2021 38
Soumen Santra

39. MergeSort (Example) - 11
11/3/2021 39
Soumen Santra

40. MergeSort (Example) - 12
11/3/2021 40
Soumen Santra

41. MergeSort (Example) - 13
11/3/2021 41
Soumen Santra

42. MergeSort (Example) - 14
11/3/2021 42
Soumen Santra

43. MergeSort (Example) - 15
11/3/2021 43
Soumen Santra

44. MergeSort (Example) - 16
11/3/2021 44
Soumen Santra

45. MergeSort (Example) - 17
11/3/2021 45
Soumen Santra

46. MergeSort (Example) - 18
11/3/2021 46
Soumen Santra

47. MergeSort (Example) - 19
11/3/2021 47
Soumen Santra

48. MergeSort (Example) - 20
11/3/2021 48
Soumen Santra

49. MergeSort (Example) - 21
11/3/2021 49
Soumen Santra

50. MergeSort (Example) - 22
11/3/2021 50
Soumen Santra

51. 14 23 45 98 6 33 42 67
11/3/2021 51
Soumen Santra

52. Merge
23 45 98 33 42 67
14 6
11/3/2021 52
Soumen Santra

53. Merge
23 45 98 6 42 67
6
14 33
11/3/2021 53
Soumen Santra

54. Merge
14 45 98 6 42 67
6 14
23 33
11/3/2021 54
Soumen Santra

55. Merge
14 23 98 6 42 67
6 14 23
45 33
11/3/2021 55
Soumen Santra

56. Merge
14 23 98 6 33 67
6 14 23 33
45 42
11/3/2021 56
Soumen Santra

57. Merge
14 23 98 6 33 42
6 14 23 33 42
45 67
11/3/2021 57
Soumen Santra

58. Merge
14 23 45 6 33 42
6 14 23 33 42 45
98 67
11/3/2021 58
Soumen Santra

59. Merge
14 23 45 98 6 33 42 67
6 14 23 33 42 45 67
11/3/2021 59
Soumen Santra

60. Merge
14 23 45 98 6 33 42 67
6 14 23 33 42 45 67 98
11/3/2021 60
Soumen Santra

61. THANK YOU
GIVE FEEDBACK