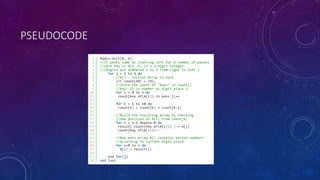
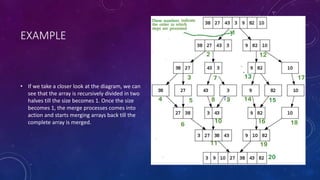
Radix sort and merge sort are sorting algorithms. Radix sort sorts data with integer keys by grouping keys by the individual digits. It has linear time complexity and is very fast, but only works for integers. Merge sort divides an array in half recursively until the subarrays contain one element, then merges the subarrays back together in sorted order. It has time complexity of O(n log n) in all cases and is easy to implement, but requires additional space.

1. RADIX AND MERGE SORT
C365 – IT ELECTIVE 4 (ANALYSIS OF ALGORITHM)

2. RADIX SORT
C365 - IT ELECTIVE 4 (ANALYSIS OF ALGORITHM)

3. WHAT IS RADIX SORT?
• Radix sort is a non-comparative sorting algorithm that sorts data with integer keys by grouping keys by
the individual digits which share the same significant position and value.
• It is one of the most efficient and fastest linear sorting algorithms.

4. COMPLEXITY
• The complexity of radix sort is linear, which in terms of omega means O(n). That is a great benefit in
performance compared to O(n.log(n)) or even worse with O(n2).

5. ADVANTAGES OF RADIX SORT
• Fast
• Radix sort is very fast compared to other sorting algorithms. This algorithm is very useful in practice because in
practice we often sort sets of integers.
• Easy to understand and implement
• Even a beginner can understand and implement radix sort, which is great. You need no more than few loops to
implement it.

6. DISADVANTAGES OF RADIX SORT
• Works only with integers
• If you’re not sure about the input better do not use radix sort. We may think that our input consists only of
integers and we can go for radix sort, but what if in the future someone passes floats or strings to our routine.
• Requires additional space
• Radix sort needs additional space – at least as much as the input.

7. PSEUDOCODE

8. EXAMPLE
• For 1st pass: we sort the array on basis of least
significant digit (1s place) using counting sort.
Notice that 435 is below 835, because
435 occurred below 835 in the original list.

9. EXAMPLE
• For 2nd pass: we sort the array on basis of next
digit (10s place) using counting sort. Notice that
here 608 is below 704, because 608 occurred
below 704 in the previous list, and similarly for
(835, 435) and (751, 453).

10. EXAMPLE
• For 3rd pass: we sort the array on basis of most
significant digit (100s place) using counting sort.
Notice that here 435 is below 453, because 435
occurred below 453 in the previous list, and
similarly for (608, 690) and (704, 751).

11. MERGE SORT
C365 - IT ELECTIVE 4 (ANALYSIS OF ALGORITHM)

12. WHAT IS MERGE SORT?
• Merging is the process of taking two smaller sorted lists and combining them together into a single,
sorted, new list.
• Merge sort is a recursive algorithm that continually splits a list in half. If the list is empty or has one
item, it is sorted by definition (the base case). If the list has more than one item, we split the list and
recursively invoke a merge sort on both halves. Once the two halves are sorted, the fundamental
operation, called a merge, is performed.

13. COMPLEXITY
• Merge Sort is a recursive algorithm and time complexity can be expressed as following recurrence
relation.
• 𝑇 𝑛 = 2𝑇 (𝑛/2) + θ(𝑛)
• Time complexity of Merge Sort is 𝜃(𝑛𝐿𝑜𝑔𝑛) in all 3 cases (worst, average and best) as merge sort
always divides the array in two halves and take linear time to merge two halves.

14. ADVANTAGES OF MERGE SORT
• Merge sort is a great sorting algorithm mainly because it’s very fast and stable. It’s complexity is the
same even in the worst case and it is O(n*log(n)).
• Merge sort is easy to implement. Indeed most of the developer consider something fast to be difficult
to implement.

15. DISADVANTAGES OF MERGE SORT
• In many implementations, if the list is N long, then it needs 2 x N memory space to handle the sort.
• If recursion is used to code the algorithm then it uses twice as much stack memory as quicksort - on the
other hand it is not difficult to code using iteration rather than recursion and so avoid the memory
penalty.
• Need for the temporary array to store the merged elements, which requires O(N) space.

16. PSEUDOCODE

17. EXAMPLE
• If we take a closer look at the diagram, we can
see that the array is recursively divided in two
halves till the size becomes 1. Once the size
becomes 1, the merge processes comes into
action and starts merging arrays back till the
complete array is merged.