The document provides a comprehensive overview of stacks in data structures, detailing their properties, operations (push, pop, peek), and implementation in C programming language. It also covers concepts like stack overflow and underflow, along with examples for converting infix expressions to postfix. Additionally, it discusses algorithm terminology and an example of string recognition using stacks.

1. Stacks
CS 308 – Data Structures

2. What is a stack?
• It is an ordered group of homogeneous items of elements.
• Elements are added to and removed from the top of the
stack (the most recently added items are at the top of the
stack).
• The last element to be added is the first to be removed
(LIFO: Last In, First Out).

3. Stack
• Stack operations may involve initializing the
stack, using it and then de-initializing it. Apart
from these basic stuffs, a stack is used for the
following two primary operations −
•  push() − Pushing (storing) an element on the
stack.
•  pop() − Removing (accessing) an element from
the stack.
• When data is PUSHed onto stack.
• To use a stack efficiently, we need to check the
status of stack as well. For the same

4. •  peek() − get the top data element of the stack,
without removing it.
•  isFull() − check if stack is full.
•  isEmpty() − check if stack is empty.
• At all times, we maintain a pointer to the last
PUSHed data on the stack. As this pointer
• always represents the top of the stack, hence
named top. The top pointer provides top
• value of the stack without actually removing it.

5. peek()
• Implementation of peek() function in C
programming language −
• int peek() {
• return stack[top];
• }

6. isfull()
• bool isfull() {
• if(top == MAXSIZE)
• return true;
• else
• return false;
• }

7. isempty()
• Implementation of isempty() function in C programming
language is slightly different. We initialize top at -1, as the
index in array starts from 0. So we check if the top is
below zero or -1 to determine if the stack is empty. Here's
the code −
• bool isempty() {
• if(top == -1)
• return true;
• else
• return false;
• }

8. Push Operation
• The process of putting a new data element onto
stack is known as a Push Operation. Push
• operation involves a series of steps −
•  Step 1 − Checks if the stack is full.
•  Step 2 − If the stack is full, produces an error
and exit.
•  Step 3 − If the stack is not full, increments top
to point next empty space.
•  Step 4 − Adds data element to the stack
location, where top is pointing.
•  Step 5 − Returns success.

9. Impelementation in C
• void push(int data) {
• if(!isFull()) {
• top = top + 1;
• stack[top] = data;
• }else {
• printf("Could not insert data, Stack is
full.n");
• }
• }

11. Pop Operation
• Accessing the content while removing it from the
stack, is known as a Pop Operation. In an array
implementation of pop() operation, the data
element is not actually removed, instead top is
decremented to a lower position in the stack to
point to the next value. But in linked-list
implementation, pop() actually removes data
element and deallocates memory space.

12. • Step 1 − Checks if the stack is empty.
• Step 2 − If the stack is empty, produces an error
and exit.
• Step 3 − If the stack is not empty, accesses the data
element at which top is
• pointing.
• Step 4 − Decreases the value of top by 1.
• Step 5 − Returns success.
Impelementation in C

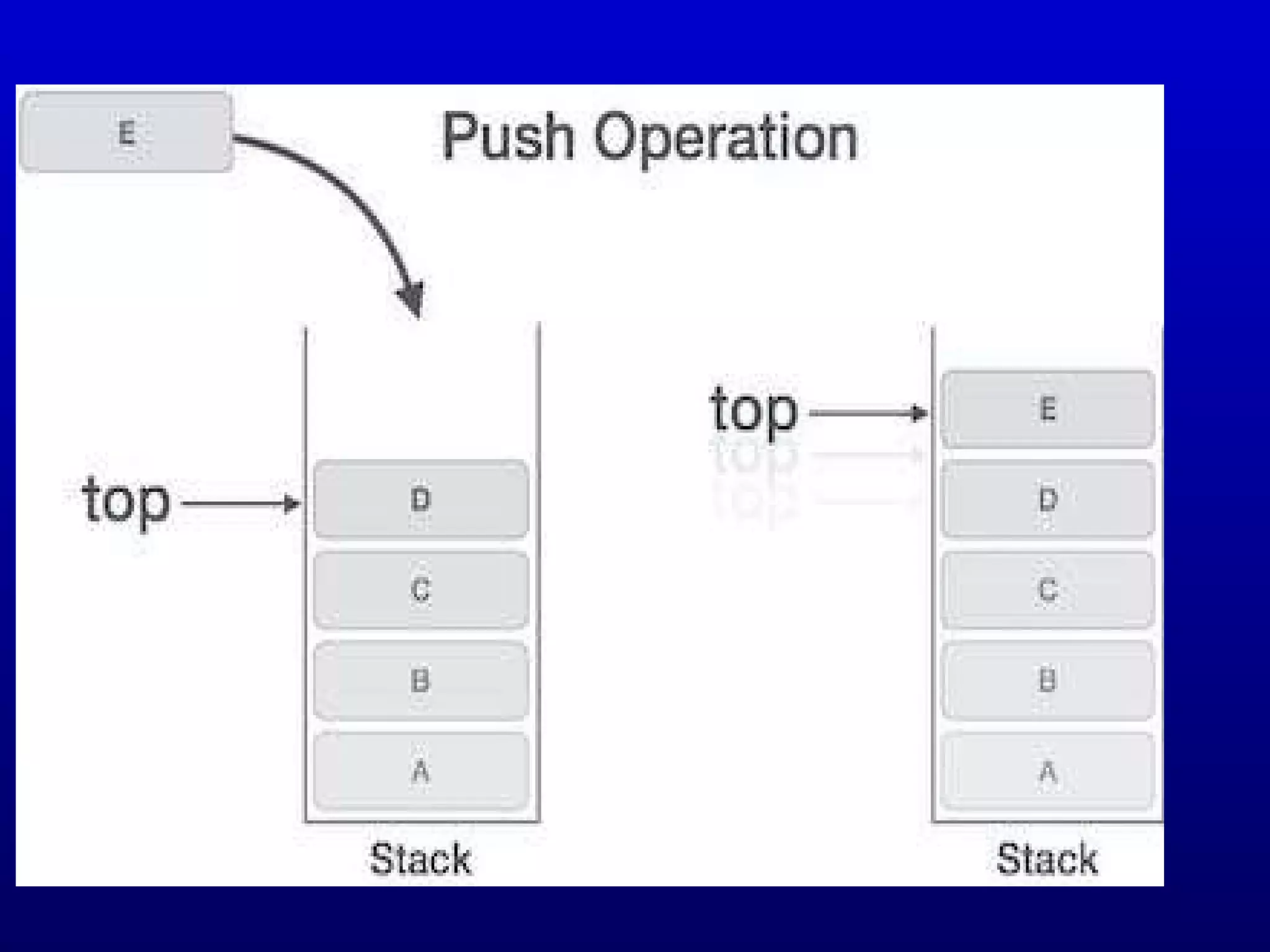
14. int pop(int data) {
if(!isempty()) {
data = stack[top];
top = top - 1;
return data;
}else {
printf("Could not retrieve data, Stack is
empty.n");
}
}

16. Stack Implementation
#include <stdio.h>
int MAXSIZE = 8;
int stack[8];
int top = -1;
int isempty() {
if(top == -1)
return 1;
else
return 0;
}
int isfull() {
if(top == MAXSIZE)
return 1;
else
return 0;
}

17. Stack Implementation (cont.)
• int peek() {
• return stack[top];
• }
• int pop() {
• int data;
• if(!isempty()) {
• data = stack[top];
• top = top - 1;
• return data;
• }else {
• printf("Could not retrieve data, Stack is empty.n");
• }

18. Stack Implementation (cont.)
int push(int data) {
if(!isfull()) {
top = top + 1;
stack[top] = data;
}else {
printf("Could not insert data, Stack is full.n");
}
}
int main() {
// push items on to the stack
push(3);
push(5);
push(9);
push(1);
push(12);
push(15);
printf("Element at top of the stack: %dn" ,peek());
printf("Elements: n");

19. //print stack data
while(!isempty()) {
int data = pop();
printf("%dn",data);
}
printf("Stack full: %sn" , isfull()?"true":"false");
printf("Stack empty: %sn" ,
isempty()?"true":"false");
return 0;
}

20. Output
• Element at top of the stack: 15
• Elements:
• 15
• 12
• 1
• 9
• 5
• 3
• Stack full: false
• Stack empty: true

21. Stack overflow
• The condition resulting from trying to push
an element onto a full stack.
if(!stack.IsFull())
stack.Push(item);
Stack underflow
• The condition resulting from trying to pop
an empty stack.
if(!stack.IsEmpty())
stack.Pop(item);

22. Expression Parsing
• The way to write arithmetic expression is known
as a notation. An arithmetic expression
• can be written in three different but equivalent
notations, i.e., without changing the
• essence or output of an expression. These
notations are −
•  Infix Notation
•  Prefix (Polish) Notation
•  Postfix (Reverse-Polish) Notation

23. Example: postfix expressions
• Postfix notation is another way of writing arithmetic
expressions.
• In postfix notation, the operator is written after the
two operands.
infix: 2+5 postfix: 2 5 +
• Expressions are evaluated from left to right.
• Precedence rules and parentheses are never needed!!

24. Example: postfix expressions
(cont.)

25. Postfix expressions:
Algorithm using stacks (cont.)

26. Postfix expressions:
Algorithm using stacks
WHILE more input items exist
Get an item
IF item is an operand
stack.Push(item)
ELSE
stack.Pop(operand2)
stack.Pop(operand1)
Compute result
stack.Push(result)
stack.Pop(result)

27. Write the body for a function that replaces each copy of an
item in a stack with another item. Use the following
specification. (this function is a client program).
ReplaceItem(StackType& stack, ItemType oldItem,
ItemType newItem)
Function: Replaces all occurrences of oldItem with
newItem.
Precondition: stack has been initialized.
Postconditions: Each occurrence of oldItem in stack has
been replaced by newItem.
(You may use any of the member functions of the
StackType, but you may not assume any knowledge of
how the stack is implemented).

28. {
ItemType item;
StackType tempStack;
while (!Stack.IsEmpty()) {
Stack.Pop(item);
if (item==oldItem)
tempStack.Push(newItem);
else
tempStack.Push(item);
}
while (!tempStack.IsEmpty()) {
tempStack.Pop(item);
Stack.Push(item);
}
}
1
2
3
3
5
1
1
5
3
Stack
Stack
tempStack
oldItem = 2
newItem = 5

29. Exercises
• 1, 3-7, 14, 12, 15, 18, 19

30. Infix to Postfix
• Infix notation is easier for humans to read
and understand whereas for electronic
machines
• like computers, postfix is the best form of
expression to parse. We shall see here a
program
• to convert and evaluate infix notation to
postfix notation
−

31. Program
• #include<stdio.h>
• #include<string.h>
• //char stack
• char stack[25];
• int top = -1;
• void push(char item) {
• stack[++top] = item;
• }
• char pop() {
• return stack[top--];
• }

32. • //returns precedence of operators
• int precedence(char symbol) {
• switch(symbol) {
• case '+':
• case '-':
• return 2;
• break;
• case '*':
• case '/':
• return 3;
• break;

33. • case '^':
• return 4;
• break;
• case '(':
• case ')':
• case '#':
• return 1;
• break;
• }
• }

34. //check whether the symbol is operator?
• int isOperator(char symbol) {
• switch(symbol) {
• case '+':
• case '-':
• case '*':
• case '/':
• case '^':
• case '(':
• case ')':
• return 1;
• break;
• default:
• return 0;
}

35. //converts infix expression to
postfix
• void convert(char infix[],char postfix[]) {
• int i,symbol,j = 0;
• stack[++top] = '#';
• for(i = 0;i<strlen(infix);i++) {
• symbol = infix[i];
• if(isOperator(symbol) == 0) {
• postfix[j] = symbol;
• j++;

36. • } else {
• if(symbol == '(') {
• push(symbol);
• }else {
• if(symbol == ')') {
• while(stack[top] != '(') {
• postfix[j] = pop();
• j++;
• }

37. • pop();//pop out (.
• } else {
• if(precedence(symbol)>precedence(stack[top])) {
• push(symbol);
• }else {
• while(precedence(symbol)<=precedence(stack[top
])) {
• postfix[j] = pop();
• j++;

38. Algorithm
• An algorithm is a sequence of finite number of steps to
solve a specific problem.
• A algorithm can be defined as well –defined step by step
computational procedure which takes set of values as
input and produce set of values as output.
• A finite set of instruction that followed to accomplish a
particular task.
38

39. Algorithm Terminology : format conventions
1. Name of algorithm:
every algorithm is given an identifying name. the
name written in capital letter.
2. Introductory comments:
the algorithms name is followed by a brief
introduction regarding the task the algorithm will
perform. in addition it also discuss some assumptions.
For example: SUM(A,N): this algorithm find the sum
of all N elements in vector A. N is integer type
variable indicate there are N elements in Vector A.
39

40. Algorithm Terminology : format conventions
3. Algorithm steps:
• Actually algorithm is a sequence of numbered steps.
• Each step is begin with a phrase enclosed in square
brackets which gives the sort description about the step.
• The phrase is followed by a set of statements which
describe action to be performed in next line.
For example
2. [ initialize variable I with 0]
I <- 0
40

41. Algorithm Terminology : format conventions
41

42. Algorithm Terminology : format conventions
42

43. Algorithm Terminology : format conventions
• Conditional Statement : IF
we can use if statement in order execute some part
algorithm based on condition.
Syntax is:
IF Condition
Then
Statement 1
Statement 2
-----------
Note: -
We can not use { } to represent the body of if statement.
43

44. Algorithm Terminology : format conventions
• Conditional Statement : IF -- else
Syntax is:
IF Condition
Then
Statement 1
Statement 2
-----------
Else
Statement 1
Statement 2
-----------
We can also form the else if ladder44

45. Algorithm Terminology : format conventions
• Repeating statements:-- looping
Three form of looping structure:
1.Repeat for index variable= sequence of values(,)
2.Repeat while <logical expression>
3.Repeat for index= sequence of values while logical exp.
1.
Repeat for I = 1,2,3,4,5,6…….10.
// set of statements
This form is used when a steps are to be repeated for a
counted number of times.45

46. Algorithm Terminology : format conventions
Repeat for I = 1,2,3,4,5,6…….10.
// set of statements
Here I is loop control variable.
Loop control variable take all values sequentially one by
one.
Once all the set of Statements are in the range are executed
,the loop control variable assume the next value in a
given sequence and again execute the same set of
statements.
No need to write I<- I+1 statement .
46

47. Algorithm Terminology : format conventions
the loop can be extended over more then one steps in
algorithm.like
1. [ ]
// set of statements
2. [ ]
Repeat thru step 4 for I= 1,2,3,..5
// set of statements
3. [ ]
// set of statements
4. [ ]
// set of statements
5. [ ]
// set of statements
47

48. Algorithm Terminology : format conventions
2. Repeat while logical expression
// set of statements
Repeat while X<10
write(X)
X <- X+1
Example:
1. [ Phrase]
// set of statements
2. [ Phrase]
Repeat while X<10
write(X)
X <- X+1
3. [ Phrase]48

49. Algorithm Terminology : format conventions
2. Repeat thru step N while logical expression
// set of statements
Repeat thru step 3 while X<10
write(X)
X <- X+1
Example:
1. [ Phrase]
// set of statements
2. [ Phrase]
Repeat thru step 3 while X<10
write(X)
X <- X+1
3. [ Phrase]49

50. Algorithm Terminology : format conventions
3. Repeat for index= sequence of values while logical exp.
// set of statements
Or Repeat thru step N for index= sequence of values
while logical exp.
// set of statements
Repeat thru step 3 for I =1,2,3 while X<10
write(X)
50

51. Algorithm Terminology : format conventions
Go to Statement:
Unconditional transfer of execution control to step
referenced.
Syntax
Goto step N
51

53. Example : Use of Stack
Example:
String Recognization :
L = { WCWR
| W ∈ { a, b}*} where WR
reverse of String W
Language L define the string of character a and b.
C will act as separator between W and WR
Forexample:
abCba, aabCbaa, abbbCbbba, -- Valid strings
abaCabb --- invalid string
53

54. String Recognization
Steps:
1. Create stack data structure
2. Read the string from the user
3.Use loop and Push the character onto stack from string
one by one until C (separator) encountered.
4. Once “C” occur in string (do not Push C on the
Stack).stop push operation.
5. Use loop, Pop one element from the stack and fetch one
character from the string after Character C.
6. Check both elements are equals or not . If both are equals
then repeat step 5 and 6 until all character in string are
fetched and top become -1. if at any moments mismatch
occur then stop process. print appropriate message. 54

55. Algorithm:
• STRRECO: given the string named str of the form WCWR
on
alphabet {a,b,C}.this algorithm determine the whether the
input string str is according to the given language rule or not. S
indicate stack and top is pointer pointing top of the stack.
• 1. [ get the string from the user and initialize the index variable
to get character one by one from the string]
• READ(str)
• I <- 0
• PUSH(S,top,’#’)
• 2.[ fetch one character at a time and push on the stack until
separator C occur in string] .
• repeat while str[i] not ‘C’
• Push(S,top, str[i])
• i <- i +1 55

56. Algorithm:
3. [scan characters following the ‘C’ one at a time and pop character
from the stack and compare]
i < i +1
repeat while s[i] not NULL
x <- POP (S , top)
if X NOT EQUAL to S[i]
then
Write ( “invalid String”)
goto step 5
4.[ compare the top and end of string simulteneously if step 3 is
successful] .
if S[i]= NULL and S[top] = ‘#’
then
write ( “String is valid”)
else write ( “invalid String”)
56

57. Algorithm:
5. [finished the algorithm]
exit
57