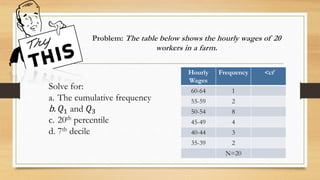
Here are the steps to solve the problem: 1. Calculate the cumulative frequency: <cf for 60-64 = 1 <cf for 55-59 = 1 + 2 = 3 <cf for 50-54 = 3 + 8 = 11 <cf for 45-49 = 11 + 4 = 15 <cf for 40-44 = 15 + 3 = 18 <cf for 35-39 = 18 + 2 = 20 2. Find Q1, Q3 and 20th percentile: a. Q1 = 50 + (4)(20)/4 - 11/8 = 47.5 b. Q3 = 50 + (12)(20)/4 - 11/12 = 52.

1. Quartiles, Deciles,
Percentiles
(Grouped data)
Objective: I can calculate a specified measure of position.

2. • Quartiles – are points that divide a distribution into 4 equal
parts. The points of separation are:
• a. 1st Quartile – also called the lower quartile and is 25% of
the observations below Q1 and 75% of the observations
above Q1.
• b. 2nd Quartile – equal to the median.
• c. 3rd Quartile – also called the upper quartile and is 75% of
the observations below Q3 and 25% of the observations
above Q3.

3. FORMULA FOR QUARTILES (Q1, Q2, and Q3)
• 𝑸 𝟏 = 𝑿 𝑳𝑩 +
𝑵
𝟒
− 𝒄𝒇 𝒃
𝒇 𝒒 𝟏
𝒊
Where:
𝑋 𝐿𝐵 = lower boundary of the Q1 class
𝑁 = total frequency
𝑐𝑓𝑏= < “cumulative frequency” before the Q1 class
𝑓𝑞1
= frequency of the Q1 class
𝑖 = size of the class intervals

4. FORMULA FOR QUARTILES (Q1, Q2, and Q3)
• 𝑸 𝟐 = 𝑿 𝑳𝑩 +
𝟐𝑵
𝟒
− 𝒄𝒇 𝒃
𝒇 𝒒 𝟐
𝒊
Where:
𝑋 𝐿𝐵 = lower boundary of the Q2 class
𝑁 = total frequency
𝑐𝑓𝑏= < “cumulative frequency” before the Q2 class
𝑓𝑞1
= frequency of the Q2 class
𝑖 = size of the class intervals

5. FORMULA FOR QUARTILES (Q1, Q2, and Q3)
• 𝑄3 = 𝑋 𝐿𝐵 +
3𝑁
4
−𝑐𝑓 𝑏
𝑓𝑞3
𝑖
Where:
𝑋 𝐿𝐵 = lower boundary of the Q3 class
𝑁 = total frequency
𝑐𝑓𝑏= cumulative frequency before the Q3 class
𝑓𝑞3
= frequency of the Q3 class
𝑖 = size of the class intervals

6. Percentile
•Percentile - are the score-points that divide a
distribution into 100 equal parts. By
definition, 𝑃50 = 𝑄2 = 𝑋 , 𝑃25 = 𝑄1 , and
𝑃75 = 𝑄3.

7. Percentile
• Some formulae:
𝑃5 = 𝑋 𝐿𝐵 +
5𝑁
100
− 𝑐𝑓 𝑏
𝑓𝑝5
𝑖
𝑃65 = 𝑋 𝐿𝐵 +
65𝑁
100
− 𝑐𝑓𝑏
𝑓𝑝65
𝑖
𝑃35 = 𝑋 𝐿𝐵 +
35𝑁
100
− 𝑐𝑓 𝑏
𝑓𝑝35
𝑖𝑃89 = 𝑋 𝐿𝐵 +
89𝑁
100
− 𝑐𝑓𝑏
𝑓𝑝89
𝑖

8. Deciles
• Deciles – are the score points that divide a distribution
into ten equal parts. They are computed in the same
way quartiles and percentiles are computed.
• Here are some formulae in solving for deciles. By
definition, 𝐷5 = 𝑃50 = 𝑄2 = 𝑋

9. Deciles
• 𝐷1 = 𝑋 𝐿𝐵 +
𝑁
10
−𝑐𝑓 𝑏
𝑓 𝑑1
𝑖 𝐷9 = 𝑋 𝐿𝐵 +
9𝑁
10
− 𝑐𝑓𝑏
𝑓𝑑9
𝑖
𝐷7 = 𝑋 𝐿𝐵 +
7𝑁
10
− 𝑐𝑓𝑏
𝑓𝑑7
𝑖

10. Solve for the 3rd quartile,
32nd percentile and 7th
decile.
Class
Interval
f <“cf
”
134-139 10 50
128-133 9 40
122-127 8 31
116-121 1 23
110-115 5 22
104-109 2 17
98-103 9 15
92-97 5 6
86-91 1 1
N=50
Find the class containing 3rd quartile, 32nd percentile and 7th
decile.
3𝑁
4
=
3(50)
4
= 37.5 → 3𝑟𝑑 𝑞𝑢𝑎𝑟𝑡𝑖𝑙𝑒 𝑐𝑙𝑎𝑠𝑠
32𝑁
100
=
)32(50
100
= 16 → 32𝑛𝑑 𝑝𝑒𝑟𝑐𝑒𝑛𝑡𝑖𝑙𝑒 𝑐𝑙𝑎𝑠𝑠
7𝑁
10
=
)7(50
10
= 35 → 𝐷7 𝑐𝑙𝑎𝑠𝑠

11. • 𝑄3 = 127.5 +
37.5−31
9
6
• 𝑄3 = 131.83
Class Interval f <“cf”
134-139 10 50
128-133 9 40
122-127 8 31
116-121 1 23
110-115 5 22
104-109 2 17
98-103 9 15
92-97 5 6
86-91 1 1
N=50
• 𝑄3 = 𝑋 𝐿𝐵 +
3𝑁
4
−𝑐𝑓 𝑏
𝑓𝑞3
𝑖Where:
𝑋 𝐿𝐵 = lower boundary of the Q3 class
𝑁 = total frequency
𝑐𝑓𝑏= cumulative frequency before the Q3 class
𝑓𝑞3
= frequency of the Q3 class
𝑖 = size of the class intervals
37.5 → 3𝑟𝑑 𝑞𝑢𝑎𝑟𝑡𝑖𝑙𝑒 𝑐𝑙𝑎𝑠𝑠
Interpretation: 75% of the respondents have a
wage lower than Php 131.83/day and 25% of them
have a wage higher than Php 131.83/day.

12. 𝑃32 = 𝑋 𝐿𝐵 +
32𝑁
100
− 𝑐𝑓𝑏
𝑓𝑝32
𝑖
Class Interval f <“cf”
134-139 10 50
128-133 9 40
122-127 8 31
116-121 1 23
110-115 5 22
104-109 2 17
98-103 9 15
92-97 5 6
86-91 1 1
N=50
16 → 32𝑛𝑑 𝑝𝑒𝑟𝑐𝑒𝑛𝑡𝑖𝑙𝑒 𝑐𝑙𝑎𝑠𝑠
𝑃32 = 103.5 +
16 − 15
2
6
𝑃32 = 106.5
Interpretation: 68% of the respondents have a
wage higher than 106.5 and 32% of them has a
wage lower than 106.5.

13. 𝐷7 = 𝑋 𝐿𝐵 +
7𝑁
10
−𝑐𝑓 𝑏
𝑓 𝑑7
𝑖
• 𝐷7 = 127.5 +
35−31
9
6
Class Interval f <“cf”
134-139 10 50
128-133 9 40
122-127 8 31
116-121 1 23
110-115 5 22
104-109 2 17
98-103 9 15
92-97 5 6
86-91 1 1
N=50
𝐷7 = 130.17
35 → 𝐷7 𝑐𝑙𝑎𝑠𝑠
Interpretation: 30% of the respondents have a
wage higher than 130.17 and 70% of them
have a wage lower than 130.17.

14. Problem: The table below shows the hourly wages of 20
workers in a farm.
Hourly
Wages
Frequency <cf
60-64 1
55-59 2
50-54 8
45-49 4
40-44 3
35-39 2
N=20
Solve for:
a. The cumulative frequency
b. 𝑄1 and 𝑄3
c. 20th percentile
d. 7th decile