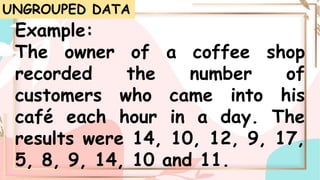
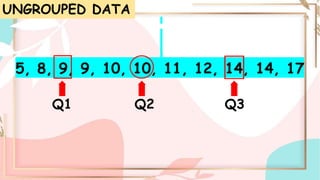
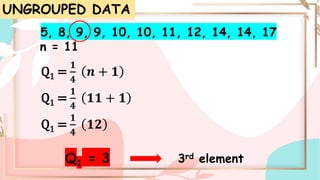
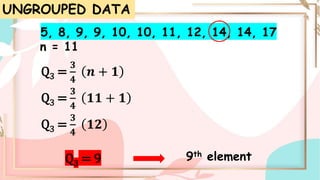
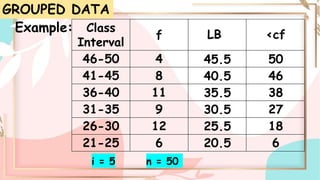
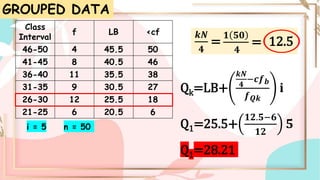
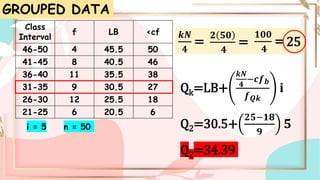
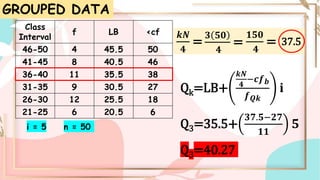
Quartiles are numbers that divide a dataset into four equal parts. The first quartile (Q1) separates the lowest 25% of data. The second quartile (Q2) is the median. The third quartile (Q3) separates the highest 25% of data. To find quartiles in an ungrouped dataset, order the numbers and take the median of each half of data. For grouped data, use a formula involving lower boundary, frequency, and cumulative frequency of each class.

1. PREPARED BY: EVERLYN R. BURCES

2. QUARTILES
These are numbers that
separate the data into
quarters, or which divide
the distribution into four
equal parts.

3. 25% of the distribution are below Q1
50% of the distribution are below Q2
75% of the distribution are below Q3
Q1 – lower quartile
Q2 – median
Q3 – upper quartile
The difference between Q3 and Q1
is called Interquartile Range.

5. Example:
The owner of a coffee shop
recorded the number of
customers who came into his
café each hour in a day. The
results were 14, 10, 12, 9, 17,
5, 8, 9, 14, 10 and 11.
UNGROUPED DATA

6. 14, 10, 12, 9, 17, 5, 8, 9, 14, 10, 11
 Steps on how to find the
quartiles for ungrouped data:
 List or arrange the data from
smallest to largest.
5, 8, 9, 9, 10, 10, 11, 12, 14, 14, 17
UNGROUPED DATA

7.  Find the median or second quartile (Q2).
5, 8, 9, 9, 10, 10, 11, 12, 14, 14, 17
 The first quartile (Q1) is the
middle value of the lower half of the
data.
 The third quartile (Q3) is the
middle value of the upper half.
UNGROUPED DATA

8. 5, 8, 9, 9, 10, 10, 11, 12, 14, 14, 17
Q1 Q2 Q3
UNGROUPED DATA

9. UNGROUPED DATA
Mendenhall & Sincich Method
Q1 =
𝟏
𝟒
𝒏 + 𝟏
 if this falls between two integers, ROUND UP.
Q3 =
𝟑
𝟒
𝒏 + 𝟏
 if this falls between two integers, ROUND
DOWN.

10. UNGROUPED DATA
5, 8, 9, 9, 10, 10, 11, 12, 14, 14, 17
n = 11
Q1 =
𝟏
𝟒
𝒏 + 𝟏
Q1 =
𝟏
𝟒
𝟏𝟏 + 𝟏
Q1 =
𝟏
𝟒
𝟏𝟐
Q1 = 3 3rd element

11. UNGROUPED DATA
5, 8, 9, 9, 10, 10, 11, 12, 14, 14, 17
n = 11
Q3 =
𝟑
𝟒
𝒏 + 𝟏
Q3 =
𝟑
𝟒
𝟏𝟏 + 𝟏
Q3 =
𝟑
𝟒
𝟏𝟐
Q3 = 9 9th element

13. Formula:
Qk=LB+
𝒌𝑵
𝟒
−𝒄𝒇𝒃
𝒇𝑸𝒌
𝐢
GROUPED DATA
Where:
LB – lower boundary of the
quartile class
N – total number of scores
cfb – cumulative frequency
before the quartile
class
fQk – frequency of the
quartile class
i – size of the class
interval
k – 𝒏𝒕𝒉
quartile

14. Example:
GROUPED DATA
Class
Interval
f
46-50 4
41-45 8
36-40 11
31-35 9
26-30 12
21-25 6
i = 5 n = 50
LB <cf
45.5
40.5
35.5
30.5
25.5
20.5
50
46
38
27
18
6

15. GROUPED DATA
Class
Interval
f LB <cf
46-50 4 45.5 50
41-45 8 40.5 46
36-40 11 35.5 38
31-35 9 30.5 27
26-30 12 25.5 18
21-25 6 20.5 6
i = 5 n = 50
Qk=LB+
𝒌𝑵
𝟒
−𝒄𝒇𝒃
𝒇𝑸𝒌
𝐢
Q1=25.5+
𝟏𝟐.𝟓−𝟔
𝟏𝟐
𝟓
Q1=28.21
𝒌𝑵
𝟒
=
𝟏 𝟓𝟎
𝟒
= 12.5

16. GROUPED DATA
Class
Interval
f LB <cf
46-50 4 45.5 50
41-45 8 40.5 46
36-40 11 35.5 38
31-35 9 30.5 27
26-30 12 25.5 18
21-25 6 20.5 6
i = 5 n = 50
Qk=LB+
𝒌𝑵
𝟒
−𝒄𝒇𝒃
𝒇𝑸𝒌
𝐢
Q2=30.5+
𝟐𝟓−𝟏𝟖
𝟗
𝟓
Q2=34.39
𝒌𝑵
𝟒
=
𝟐 𝟓𝟎
𝟒
=
𝟏𝟎𝟎
𝟒
=25

17. GROUPED DATA
Class
Interval
f LB <cf
46-50 4 45.5 50
41-45 8 40.5 46
36-40 11 35.5 38
31-35 9 30.5 27
26-30 12 25.5 18
21-25 6 20.5 6
i = 5 n = 50
Qk=LB+
𝒌𝑵
𝟒
−𝒄𝒇𝒃
𝒇𝑸𝒌
𝐢
Q3=35.5+
𝟑𝟕.𝟓−𝟐𝟕
𝟏𝟏
𝟓
Q3=40.27
𝒌𝑵
𝟒
=
𝟑 𝟓𝟎
𝟒
=
𝟏𝟓𝟎
𝟒
= 37.5