Documentul oferă o introducere detaliată în conceptul de matrice și operațiile efectuate asupra acestora, incluzând definițiile, tipurile de matrici și exemple. Se discută despre adunarea, înmulțirea și proprietățile matricilor, precum asociativitatea și comutativitatea adunării, precum și necesitatea de a avea dimensiuni compatibile pentru operațiunile de înmulțire. De asemenea, este menționată teorema Cayley-Hamilton și se prezintă concepte precum matricea nulă și matricea unitate.

1. MATRICI ŞI DETERMINANŢI
1. MATRICI
1.1. Despre matrici
Acest concept l-am întalnit înca din primul an de liceu, atunci când s-a pus
problema rexolvarii unui sistem de două ecuaţii cu două necunoscute x, y, de forma
 ax + by = c
 ' ' '.
a x+ b y = c
Acestui sistem i-am asociat un teblou pătratic, care conţine coeficienţii
necunoscutelor (în prima linie sunt coeficienţii lui x, y din prima ecuaţie, iar in a doua
ab
 ' '
ab
linie figurează coeficienţii lui x, y din ecuaţia a doua): .
 
Am numit acest tablou matrice pătratică (sau matricea sistemului). Pe cele două
coloane ale matricei figurează coeficienţii lui x (pe prima coloană a, a ' ) şi respectiv
coeficienţii lui y (pe a doua coloană b, b ' ).
Definiţie. Se numeşte matrice cu m linii şi n coloane (sau de tip m × n ) un
tablou cu m linii şi n coloane
 a11 a12 ... a1n 
 
 a21 a22 ... a2n 
 ... ... ... ... 
 
a am2 ... amn 
 m1
ale cărui elemente a ij sunt numere complexe.

2. Uneori această matrice se notează şi A = ( ai j ) unde i =1, m şi j =1, n . Pentru
elementul a ij , indicele i arată linia pe care se află elementul, iar al doilea indice j indică
pe ce coloană este situat.
Mulţimea matricilor de tip m × n cu elemente numere reale se notează prin
Μm, n ( R ) . Aceleaşi semnificaţii au şi mulţimile Μm, n ( Z ) , Μ n ( Q ) , Μ n ( C ) .
m, m,
Cazuri particulare
1) O matrice de tipul 1 ×n (deci cu o linie şi n coloane) se numeşte matrice linie şi are
forma
A = ( a1 a 2 ... a n ) .
2) O matrice de tipul m ×1 (cu m linii şi o coloană) se numeşte matrice coloană şi are
forma
 a1 
 
 a2 
B=  .
...
 
a 
 m
3) O matrice de tip m × n se numeşte nulă (zero) dacă toate elementele ei sunt zero. Se
notează cu O
 0 0 ... 0
 
 0 0 ... 0
O=  .
... ... ... ...
 
 0 0 ... 0 

4) Dacă numărul de linii este egal cu numărul de coloane, atunci matricea se numeşte
pătratică.

3.  a11 a12 ... a1n 
 
 a21 a22 ... a2n 
A=  .
... ... ... ...
 
a an2 ... ann 
 n1
Sistemul de elemente ( a11 a 22 ... a nn ) reprezintă diagonala principală a
matricii A, iar suma acestor elemente a11 + a 22 +... + a nn se numeşte urma matricii
n
A notată Tr(A) = ∑ai i . Sistemul de elemente ( a1n a 2 n −1 ... a n1 ) reprezintă
i =1
diagonala secundară a matricii A.
Mulţimea acestor matrici se notează Μn ( C ) . Printre aceste matrici una este foarte
importantă aceasta fiind
 1 0 ... 0 
 
 0 1 ... 0 
In = 
... ... ... ...
 
 0 0 ... 1 
 
şi se numeşte matricea unitate (pe diagonala principală are toate elementele egale cu 1,
iar în rest sunt egale cu 0).
1.2. Operaţii cu matrici
1.2.1. Egalitatea a două matrici
Definiţie. Fie A = ( ai j ) , B = (bi j ) ∈ Μm, n ( C ) . Spunem că matricile A, B sunt
egale şi scriem A = B dacă ai j = bi j , (∀ i =1, m , (∀ j =1, n .
) )
Exemplu: Să se determine numerele reale x, y astfel încăt să avem egalitatea de
matrici

4.  x+ 1 + yx   2 x−− 1
  =   .
 0 x− 2y  0 − 29 x
R. Matricile sunt egale dacă elementele corespunzătoare sunt egale, adică:
x+ 1= 2
x+ y = −x−1

 Rezolvând acest sistem găsim soluţia x = 1, y = -3.
0 = 0
 x − 2 y = 9 − 2 x.

1.2.2. Adunarea matricilor
Definiţie. Fie A = ( ai j ) , B = (bi j ) , C = ( ci j ) ∈ Μm, n ( C ) . Matricea C se numeşte
suma matricilor A, B dacă: c i j = a i j + bi j , (∀ i =1, m , (∀ j =1, n .
) )
Observaţii
1) Două matrici se pot aduna dacă sunt de acelaşi tip, adică dacă au acelaşi număr de
linii şi acelaşi număr de coloane, deci A, B ∈ Μm, n ( C ) .
2) Explicit adunarea matricilor A, B înseamnă:

5.  a11 a12 ... a1n   b11 b12 ... b1n 
   
 a21 a22 ... a2n   b21 b22 ... b2n 
 ... ... ... ...  +  ... ... ... ...  =
   
a am2 ... amn   bm1 bm 2 ... bmn 
 m1
 a11 + b11 a12 + b12 ... a1n + b1n 
 
 a21 + b21 a22 + b22 ... a2n + b2n 
 ... ... ... ... .
 
 a + b a + b ... a + b 
 m1 m1 m2 m2 mn mn 
Exemplu: Să se calculeze A + B pentru:
 1 − 1 2   0 5 − 3
1.
A=   , B=   ;
3 0 1 10 1 5

6.  1  0 1
2.
A=   , B=  .
− 1  1 0
R. 1. Avem
 1 − 2   0 5 − 3  1 + 0 - 5 2 - 3   1 4 − 
A+B= + = = 
3 01 0 1 5 3+10 +1 5 13 6
2. Avem

7.  1 01  +01  12
A+B= + .= =  .
− 1  0 −1+ 0  1
Proprietăţi ale adunării matricilor
A 1 (Asociativitatea adunării). Adunarea matricilor este asociativă, adică:
( A + B ) + C = A + ( B + C ) , (∀ A, B, C ∈ Μm,n (C ) .
)
A 2 (Comutativitatea adunării). Adunarea matricilor este comutativă, adică:
A + B = B + A , (∀ A, B ∈ Μm, n ( C ) .
)
A 3 (Element neutru). Adunarea matricilor admite matricea nulă ca element
neutru, adică ∃ Om ,n ∈ Μm, n ( C ) astfel încât A + Om ,n = A, (∀ A ∈
)
Μ n (C ) .
m,
A 4 (Elemente opuse). Orice matrice A ∈ Μm, n ( C ) are un opus, notat − A ,
astfel încât
A + ( − A ) = Om , n .
1.2.3. Înmulţirea cu scalari a matricilor
Definiţie.Fie λ ∈ C şi A = ( a i j ) ∈ Μm, n ( C ) . Se numeşte produsul dintre
scalarul λ ∈ C şi matricea A, matricea notată λA ∈ Μm, n ( C ) definită prin λA =
(λai j ) .

8. Obs.: A înmulţi o matrice cu un scalar revine la a înmulţi toate elementele matricii cu acest scalar.
 λ a11 λ a12 ... λ a1n 
 
 λ a21 λ a22 ... λ a2n 
Deci λA =
 ... ... ... ...  .
 
 λ a λ a ... λ a 
 m1 m2 mn 
1 
 − 3 5
2  . Atunci 6A =  3 − 18 30
Exemplu Fie A = 
 2 
  .
 0 1
 3 
0 4 6
Proprietăţi ale înmulţirii matricilor cu scalari
S 1 λ( µA) = ( λµ ) A , (∀ λ µ∈ C, (∀ A ∈ Μm, n ( C ) ;
) , )
S2 λ ( A + B ) = λA + λB , (∀ λ ∈ C, (∀ A, B ∈ Μ n ( C ) ;
) ) m,
S 3 ( λ + µ ) A = λA + µA , (∀ λ µ∈ C, (∀ A ∈ Μ n ( C ) ;
) , ) m,
S4 1 ⋅ A = A ,1 ∈ C, (∀ A ∈ Μm, n (C ) ;
)
1.2.4. Înmulţirea matricilor
Definiţie. Fie A = ( a k i ) ∈ Μm, n ( R ) , B = (bi j ) ∈ Μn, p ( R ) . Produsul dintre
matricile A şi B (în aceasta ordine), notat AB este matricea C = (c k j ) ∈ Μm, p ( R )
definită prin
n
c k j = ∑ a k i bi j , (∀ k
) = ,m
1 , (∀) j = ,n .
1
i =1
Observaţii
1) Produsul AB a două matrici nu se poate efectua întotdeauna decât dacă A ∈ Μm, n ( R ) ,
B ∈ Μn, p ( R ) , adică numărul de coloane ale lui A este egal cu numărul de linii ale lui
B, când se obţine o matrice C = AB ∈ Μm, p ( R ) .

9. 2) Dacă matricile sunt pătratice A, B ∈ Μn ( R ) atunci are sens întotdeauna atât AB cât şi
BA, iar, în general, AB ≠ BA adică înmulţirea matricilor nu este comutativă.
Proprietăţi ale înmulţirii matricilor
I 1 (Asociativitatea înmulţirii). Înmulţirea matricilor este asociativă, adică
( AB )C = A( BC ) , (∀ A ∈ Μm,n (C ) , (∀ B ∈ Μn, p (C ) , (∀ C ∈
) ) )
Μp , s (C ) .
I 2 (Distributivitatea înmulţirii în raport cu adunarea). Înmulţirea
matricilor este distributivă în raport cu adunarea matricilor, adică
( A + B )C = AC + BC , C ( A + B ) = CA + CB, (∀ A, B, C matrici
)
pentru care au sens operaţiile de adunare şi înmulţire.
I 3 Dacă I n ∈ Μn ( C ) este matricea unitate, atunci
I n A = AI n = A, (∀ A ∈ Μn ( C ) .
)
Se spune că I n este element neutru în raport cu operaţia de înmulţire a matricilor.
1.2.5. Puterile unei matrici
Definiţie. Fie A ∈ Μn ( C ) . Atunci A1 = A , A2 = A ⋅ A , A 3 = A 2 ⋅ A , …,
A n = A n −1 ⋅ A , (∀ n ∈ N * . (Convenim A = I 2 ).
) 0
TEOREMA Cayley – Hamilton. Orice matrice A ∈ Μn ( C ) îşi verifică
polinomul caracteristic det ( A − λI ) = 0 .
Pentru n = 2.
 a b a b
A =   ⇒ det A = = ad − bc
 c d c d

10. ab 10  − λ ba 
A− λI=  − λ =   .
c d 01  c d− λ
a− λ b
det − λ IA = 0⇔ = 0 ( )(da λλ )−−−⇔ bc= 0 ad (a d)λ −++−⇒ bc= 0⇒
2
dc − λ
⇒ λ2 − ( a + d ) λ + ad − bc = 0
polinom caracteristic
Generalizat.
A n − ( TrA) ⋅ A n −1 + ( det A) ⋅I n = 0
2. DETERMINANŢI
2.1. Definiţia determinantului de ordin n ≤ 4
Fie A= ( a i j ) ∈ Μn ( C ) o matrice pătratică. Vom asocia acestei matrici un număr
notat det(A) numit determinantul matricii A.

11. Definiţie. Dacă A= ( a11 ) ∈ Μn ( C ) este o matrice pătratică de ordinul întâi,
atunci
det(A) = a11 .
 a11 a12 
Definiţie. Determinantul matricii A =   este numărul
 a21 a22 
a11 a12
det ( A) = a11 a 22 − a12 a 21 =
a21 a22
şi se numeşte determinant de ordin 2. Termenii a11 a 22 , a12 a 21 se numesc termenii
dezvoltării determinantului de ordin 2.
Definiţie. Determinantul matricii
 a11 a12 a13 
 
A =  a21 a22 a23  este numărul
a a a 
 31 32 33 
det( A) = a11 a 22 a 33 + a13 a 21 a32 + a12 a 23 a31 − a13 a 22 a31 − a12 a 21 a33 − a11 a 23 a 32
şi se numeşte determinant de ordin 3. Termenii care apar în formulă se numesc termenii
dezvoltării determinantului.
Pentru calculul determinantului de ordin trei se utilizează trei tehnici simple:
Regula lui Sarrus
Fie determinantul de ordin 3, d =a i j i , j =, 3
1
. Pentru a calcula un astfel de
determinant se utilizează tabelul de mai jos.

12. a11 a12 a13
(am scris sub determinant
a21 a22 a23 primele două linii)
a31 a32 a33
Se face produsul elementelor de pe diagonale.
a a a
11 12 13
Produsul elementelor de pe o diagonală descendentă este
cu semnul plus. Avem trei astfel de produse:
a11 a 22 a 33 , a13 a 21 a 32 , a12 a 23 a31 .
a a a
21 22 23 Produsul elementelor de pe o diagonală ascendentă este
cu semnul minus. Avem trei astfel de produse:
− a13 a 22 a 31 , − a12 a 21 a 33 , − a11 a 23 a 32 .
Suma celor şase produse dă valoarea determinantului d de ordin 3. Acest
procedeu de calcul se numeşte „regula lui Sarrus”.
Regula triunghiului
Am văzut că determinantul de ordin trei are în dezvoltarea sa şase termeni, trei cu
semnul plus şi alţi trei cu semnul minus.
Primul termen cu plus se găseşte înmulţind elementele de pe diagonala principală,
iar ceilalţi doi, înmulţind elementele situate în vârfurile celor două triunghiuri care au o
latură paralelă cu cu diagonala principală. După aceeaşi regulă, referitoare la diagonala
secundară, se obţin termenii cu minus.
Obs.: Atât „regula lui Sarrus” cât şi „regula triunghiului” se aplică numai determinanţilor de ordin 3.
Exemplu. Să se calculeze prin cele două metode de mai sus determinantul
−3 0 1
d= 0 2 −1
31 0
R. Regula lui Sarrus.
d = −3 ⋅ 2 ⋅ 0 + 0 ⋅ 1 ⋅ 1 + 3 ⋅ 0 ⋅ (−1) − [ 3 ⋅ 2 ⋅ 1 + ( −3) ⋅ 1 ⋅ (−1) + 0 ⋅ 0 ⋅ 0] = 0 + 0 + 0 − ( 6 + 3 + 0) = −9
Regula triunghiului
d = −3 ⋅ 2 ⋅ 0 + 0 ⋅ (−1) ⋅ 3 + 0 ⋅ 1 ⋅ 1 − [ 3 ⋅ 2 ⋅ 1 + ( −3) ⋅ 1 ⋅ (−1) + 0 ⋅ 0 ⋅ 0] = 0 + 0 + 0 − ( 6 + 3 + 0) = −9
Recurent (sau dezvoltare după o linie sau o coloană)
Determinantul de ordin 3 are 6 ( = 3!) termeni dintre care trei sunt cu semnul plus,
iar ceilalţi cu semnul minus.
Are loc următoarea proprietate:

13. a1+ 2 23 1+2 a21 3 1+3 a21 2
det(A)= −1) a1 +(−1) a12 +(−1) a13 , (1)
a32 3 a31 a31 2
a1+ 2 23 2+1 a12 3 3+1 a12 3
=
(−1) a1 + (−1) a21 + (−1) a31 . (2)
a32 3 a32 3 a2 3
Observaţii

14. 1) Egalitatea (1) se mai numeşte dezvoltarea determinantului după elementele liniei
întâi, iar egalitatea (2) se numeşte dezvoltarea determinantului după elementele
coloanei întâi.
2) Formulele (1) şi (2) sunt relaţii de recurenţă, deoarece determinantul de ordin 3 se
exprimă cu ajutorul unor deteminanţi de ordin inferior (2).
2.2. Definiţia determinantului de ordin n
Voi defini în continuare determinantul de ordin n prin recurenţă cu ajutorul
determinanţilor de ordin n – 1. Pentru aceasta sunt necesare unele precizări.
Fie A= ( ai j ) ∈ Μn ( C ) .
Definiţie1. Se numeşte minor asociat elementului ai j determinantul matricii
pătratice Ai j de ordin n – 1 obţinut prin suprimarea liniei i şi coloanei j din matricea A.
Se notează acest minor prin det ( Ai j ) sau Di j .
Definiţie2. Se numeşte complement algebric al elementului ai j numărul
( −1) i + j det ( Ai j ) . Exponentul i + j al lui (–1) este suma dintre numărul liniei i şi coloanei
j pe care se află ai j .
Definiţie. Determinantul matricii A= ( a i j ) de ordin n este suma produselor
elementelor din prima linie cu complemenţii lor algebrici adică
det ( A) = a11 D11 − a12 D12 + a13 D13 + ... + ( −1) a1n D1n .
n +1
Observaţii
1) Elementelor, liniilor şi coloanelor matricii A le vom spune de asemenea elementele,
liniile şi coloanele determinantului
a11 a12 ... a1n
a21 a22 ... a2n
det( A) = .
... ... ... ...
an1 an2 ... ann
2) Formula din definiţie spunem că reprezintă dezvoltarea determinantului de ordin n
după elementele primei linii.
3) Definiţia determinantului de mai sus este încă puţin eficientă (o voi ilustra mai jos
pentru n = 4). De aceea se impune stabilirea unor proprietăţi ale determinanţilor care să
fie comode atât din punct de vedere al teoriei şi din punct de vedere calculatoriu. Aceste
proprietăţi le prezint în paragraful următor.

15. 4) Continuând cu explicitarea determinanţilor de ordin n – 1 din definiţie
( D11 , D12 ,..., D1n ) se obţine pentru det( A) o sumă de produse de elemente din
determinant, fiecare produs conţinând elemente situate pe linii şi coloane diferite.
5) Determinantul este o funcţie det : Μ n ( C ) → C .
Exemplu Să se calculeze determinantul de ordin 4:
1 0 −1 2
1 −2 0 0
d= .
0 1 1 −1
1 −1 0 0
R. Aplicăm definiţia dată mai sus pentru n = 4 şi dezvoltăm determinantul după
elementele liniei întâi. Avem:
−2 0 1 0 1−2 0 1−2 0
d=1⋅ 1− 0⋅ 1 − +( 1)⋅0 1− 2⋅0 1 =
−1 0 1 0 1 − 0 1 − 0
= 0 − 0 −1 + 2 = 1 ,

16. unde determinanţii de ordin 3 i-am calculat prin una din metodele prezentate la
determinanţii de ordin 3.
2.3. Proprietăţile determinanţilor
P1 . Determinantul unei matrici coincide cu determinantul matricii transpuse,
adică dacă A ∈ Μn ( C ) , atunci det ( A) = det ( t A) .
 a b  a c
Demonstraţie. Fie A =   şi
t
A =   .
 c d  b d
Atunci det ( A) = ad − bc , iar det ( t A) = ad − bc . Prin urmare det ( A) = det ( t A) .
P2 . Dacă toate elementele unei linii (sau coloane) dintr-o matrice sunt nule,
atunci determinantul matricii este nul.
00 0b
Demonstraţie. Avem 0 d 0 c =⋅−⋅= 0 0 d 0 b=⋅−⋅= 0
şi .
dc 0 d
P3 . Dacă într-o matrice schimbăm două linii (sau două coloane) între ele
obţinem o matrice care are determinantul egal cu opusul determinantului matricii iniţiale.
dc ba
Demonstraţie. Prin schimbarea liniilor să arăt că avem egalitatea
= .
ba dc
Avem evident bc − ad = −( ad − bc ) .

17. P4 . Dacă o matrice are două linii (sau coloane) identice, atunci determinantul
său este nul.
Demonstraţie. Verific pentru linii (şi tot odată pentru coloane). Avem:
ba
ba ba =⋅−⋅= 0 .
ba
P5 . Dacă toate elementele unei linii (sau coloane) ale unei matrici sunt înmulţite
cu un număr α , obţinem o matrice al cărei determinant este egal cu α înmulţit cu
determinantul matricii iniţiale.
Demonstraţie. Verificăm pentru linii proprietatea.
αα ⋅⋅ ba a b
= ⋅ad− ⋅bc ααα (ad bc)=−= α .
dc c d
P6 . Dacă elementele a două linii (sau coloane) ale unei matrici sunt
proporţionale, atunci determinantul este nul.
Demonstraţie. Verificăm pentru linii.
a b ab
= λ λ (ab ab)=−= 0 .
λλ ba a b

18. P7 . Dacă linia i a unei matrici A este suma a doi vectori, atunci determinantul ei
este egal cu suma a doi determinanţi corespunzători matricelor care au aceleaşi linii ca A,
cu excepţia liniei i unde au câte unul din cei doi vectori.
a1 . a1n a1 . a1n a1 . a1n
. . . .. . ...
ai1 + bi1 . ain + bin = ai1 . ain + bi1 . bin .
. . . .. . ...
an1 . an an1 . an an1 . an
Demonstraţie. Am de arătat că:

19. + aa b+ a b ba
' ' ''
=+ .
c d c d dc
Într-adevăr membrul stâng este egal cu ( a + a ' )d − c(b + b ' ) = ad + a ' d − bc − b ' c .
Membrul drept este ad − bc + a ' d − b ' c şi egalitatea se verifică.
Obs.: O proprietate analogă are loc şi pentru coloane.
P8 . Dacă o linie (o coloană) a unei matrici pătratice este o combinaţie liniară de
celelalte linii (coloane), atunci determinantul matricii este zero.
P9 . Dacă la o linie (o coloană) a matricii A adunăm elementele altei linii
(coloane) înmulţite cu acelaşi număr, atunci această matrice are acelaşi determinant ca şi
matricea A.
Demonstraţie. Voi aduna la linia întâi L1 linia a doua înmulţită cu λ .
Vom nota acest fapt prin L1 + λL2 . Avem:

20. a+λ b 11 ab λ1 b a ab
P7 + P6 +0= .
a b11 a1b 1 b a1 a1b
P10 . det ( I n ) = 1
P11 . det ( λA) = λn det ( A), A ∈ Μn ( C ) .
P12 . Dacă A= ( ai j ) este o matrice triunghiulară (sau diagonală), atunci
det ( A) = a11 a 22 ...a nn . (Valoarea determinantului este egală cu produsul elementelor de
pe diagonala principală).
P13 . Dacă A, B ∈ Μn ( C ) , atunci det ( AB ) = det ( A) ⋅ det ( B ) (Determinantul
produsului a două matrici pătratice este egal cu produsul determinanţilor acelor matrici).
În particular det ( A n ) = ( det ( A) ) n , n ∈ N * .

21. Teoremă. Determinantul unei matrici A ∈ Μn ( C ) este egal cu suma produselor
dintre elementele unei linii Li (i =1, n ) şi complemenţii lor algebrici, adică
det ( A) = a i1 ( − 1) Di1 − a i 2 ( − 1) Di 2 + a i 3 ( − 1) Di 3 + ... + a in ( − 1) Din .
i +1 i +2 i +3 i +n
(Formula lui det ( A) dă dezvoltarea determinantului după elementele liniei i).
Această teoremă permite să calculăm determinantul unei matrici după oricare
linie. Se va alege acea linie care are mai multe zerouri sau pe care se pot realiza (cât mai
uşor) mai multe zerouri.
Observaţie: Ţinând seama de proprietatea P1 teorema precedentă are loc şi
pentru coloane sub forma:
det ( A) = a1 j ( −1) D1 j − a 2 j ( −1) D2 j + a 3 j ( −1) D3 j + ... + a nj ( −1)
1+ j 2+ j 3+ j n+ j
Dnj .
2.4. Calculul inversei unei matrici
Definiţie. Fie A ∈ Μn ( C ) . Matricea A se numeşte inversabilă dacă există
matricea B ∈ Μn ( C ) cu proprietatea că A ⋅ B = B ⋅ A = I n , I n fiind matricea unitate.
Matricea B din definiţie se numeşte inversa matricii A şi se notează B = A −1 .
Deci
A ⋅ A −1 = A −1 ⋅ A = I n .
Teoremă. Matricea A ∈ Μn ( C ) este inversabilă dacă şi numai dacă
det ( A) ≠ 0. O astfel de matrice se numeşte nesingulară.
Construcţia lui A −1 presupune următorii paşi:
Pasul 1. (Construcţia transpusei)
 a11 a12 ... a1n 
 
 a21 a22 ... a2n 
Dacă A =
 ... ... ... ... ,
 
a an2 ... ann 
 n1

22.  a11 a12 ... an1 
 
t  12
a a22 ... an2 
atunci construim transpusa lui A A =
 ... ... ... ... .
 
a a2n ... ann 
 1n
Pasul 2. (Construcţia adjunctei)
 ( − 1) 1+ 1 D11 ( − 1) 1+ 2 D12 ... ( − 1) D1n 
1+ n
 
 ( − 1) 2+ 1 D ( − 1) 2+ 2 D ... ( − 1) 2+ n D2n 
Matricea A = 
* 21 22

 ... ... ... ... 
 n+ 1 n+ n 
 ( − 1) Dn1 ( − 1) n+ 2 Dn2 ... ( − 1) Dnn 
obţinută din t A , inlocuin fiecare element cu complementul său algebric se numeşte
adjuncta matricii A.
Pasul 3. (Construcţia inversei) Se ţine cont de teorema precedentă şi se găseşte că:
 d 0 0 .. 0 
 
*  0 d 0 .. 0 
A ⋅ A = A⋅ A = 
*
, iar de aici  d A  A = A d A  = I .
1 1
.. .. .. .. ..
* *
n
 
 0 0 0 .. d
 
1
A −1 = ⋅ A*
det ( A)
Ultimele egalităţi arată că

23. 2.5. Ecuaţii matriciale
Voi prezenta în continuare o tehnică de rezolvare a unor ecuaţii de forma
AX = C , XA = C , AXB = C , unde A, B, C sunt matrici cunoscute, iar X este matricea
de aflat. Astfel de ecuaţii se numesc ecuaţii matriciale.
Astfel de ecuaţii se pot rezolva numai atunci când A, B sunt matrici pătratice
inversabile.
Pentru rezolvarea ecuaţiei AX = C înmulţim la stânga egalitatea cu A −1 şi
avem:
( )
A −1 ( AX ) = A −1C ⇔ A −1 A X = A −1C ⇔ IX = A −1C ⇔ X = A −1C .
−1
Deci soluţia ecuaţiei date este X = A C .
Pentru determinarea soluţiei ecuaţiei XA = C vom înmulţi la dreapta cu A −1 şi
analog vom găsi X = CA −1 , soluţia ecuaţiei matriciale.
Pentru găsirea soluţiei ecuaţiei AXB = C înmulţim egalitatea la stanga cu A −1 şi
la dreapta cu B −1 şi obţinem X = A −1CB −1 .

24. APLICAŢII
1. Manual
pg. 67 Să se determine numerele reale x, y, z astfel încât să aibă loc egalitatea de
matrici, în cazurile

25.  1 2x− 3y  1 xy −− 1 
1)
  =  
7 x+− 6y 0  19 0
1 = 1

 2 x − 3 y = y − x − 11 ⇒ 3x = 4 y − 11 ⇒ x = 4 y − 11
 3
⇒
 − 7 x + 6 y = 19 ⇒ − 7 ⋅ 4 y − 11 + 6 y = 19 ⇒ 77 − 28 y + 18 y = 57 ⇒ 10 y = 20 ⇒ y = 2
 3
0 = 0

4 y − 11
x=  8 − 11
3  ⇒ x= ⇒ x= −1
3
dar y = 2 
 2x 3 + yx   y+ 3 8− y
2)
  =  
x − 7y 2x  − 5 4y

26.  2x = y + 3 ⇒ 2 ⋅ 2 y = y + 3 ⇒ 3y = 3 ⇒ y = 1
 3x + y = 8 − y

⇒
 x − 7y = − 5
 2x = 4 y ⇒ x = 2 y

x = 2y 
 ⇒ x= 2
dar y = 1
 y + 3 x − 1  x + 1 − 1
2
3)
  =  
 3 − xy   3 6
 y + 3x = x 2 + 1 ⇒ 6 + x + 3x = x 2 + 1 ⇒ x 2 − 4 x − 5 = 0

− 1= −1
⇒
3 = 3
 y− x = 6⇒ y = 6+ x

x 2 − 4 x − 5 = 0 ⇒ x 2 − 5 x + x − 5 = 0 ⇒ x( x − 5) + ( x − 5) = 0 ⇒ ( x − 5)( x + 1) = 0 ⇒ x1 = 5
⇒ x 2 = −1
I. dacă x = 5 , atunci y =11
II. dacă x = −1 , atunci y = 5

27.  xy 0  xz−− 5 0
4)
  =  
y z+ yx zx− 3  4 − zy
 xy = − xz − 5 ⇒ x( y + z ) + 5 = 0
0= 0

  3   x 2 + xy + 3 
⇒  yz + yx = 4 ⇒ y( x + z ) − 4 = 0 ⇒ y x +  = 4 ⇒ y  = 4 ⇒ x 2 y + y 2 x + 3 y = 4 x + 4 y
  x+ y  x+ y 
 3
 zx − 3 = − zy ⇒ z( x + y ) − 3 = 0 ⇒ z =
 x+ y
pg. 71 1. Să se calculeze A + B în cazurile:
 1 − 3  2 4 
1) A =   B =  
, .
 0 4   − 5 − 3

28.  + 21 +− 43   3 1
BA =+   BA =+⇒  
0 + (− 5) 4+ (− 3)  − 5 1
 1+ i − i 3i   − 1− 3i 2 + i 1
2) A =   B =  , 
 0 − 1− i i  i 1+ i − i 
 1 i ( 1−−++ 3i) i 2++− i i+ 13   − 2i 2 i+ 13 
A B=+   ⇒ A B=+  
 0+ i 1 i 1++−− ii −+ i)(   i 0 0
2. Se consideră matricile

29.  2 m − 2 2  n m 1 − 1   − 1 − 4 − 1 1
     
A =  4 − 1 2m 5  , B =  − 4 0 6 − 3  , C =  0 − 1 − m 2  .
 2 10 − 12 1   − 1 − 5 6 0   p 5 − 6 1 
     
Să se determine m, n, p astfel încât A + B = C .
2 + n = −1⇒ n = −3
 m + m = − 4 ⇒ 2m = − 4 ⇒ m = − 2

⇒ .
 2m + 6 = − m
2 − 1= p ⇒ p = 1

n = −3

Deci  m = − 2
p=1

pg. 75 1. Se consideră matricile A, B ∈Μ 2,3 (C ) .
 1 i − 1  − i 1 0
A =   , B =   .
 0 2 3i  1 i i + 1
Să se calculeze: 3 A − 2iB , iA + 2 B .

30.  1 i −   1 0   3 i −   2 i 0  1 i − 3 
3A−2iB= −2i = + = 
023i 1 i+069i−2 i−287i+

31.  1 i −  1 0   i − 1 2i 0   − i 1 
iA+2B= +2 = + = 
023i 1 +02i−3 2i +24i −1
pg. 87 1. Calculaţi produsele de matrici A ⋅ B , unde
3 1
 2 1 1  
 3 0 1 şi B =  2 1 
a) A =  
  1 0
 
 6 + 2 + 1 2 +1 + 0   9 3
AB = 
 9 + 0 + 1 3 + 0 + 0  = 10 3 
  
   
2 
 
b) A = 1  şi B = (1 2 3)
3 
 

32.  2 4 6
 
AB =  1 2 3 
 3 6 9
 
 1 i i − 3i 
c) A = 
  şi B = 
 0 
 − 2i 0  1  
 1⋅ i + i ⋅ 0 − 3i ⋅ 1 + i ⋅ 1   i − 2i 
AB = 
 − 2i ⋅ i + 0 ⋅ 0 − 2i ⋅ ( − 3i ) + 0 ⋅ 1 =  2 − 6 
  
   
4 2 −1   2 
   
d) A =  3 −4 6  şi B =  − 4 
5 2 −7   5 
   
 −5 
 
AB =  52 
 − 33 
 
3 4 9  5 6 4 
   
e) A = 5 −1 6  şi B =  8 9 7 
5 3 5 − 4 − 5 −3
   
 11 9 13 
 
AB =  − 22 − 27 −17 
 29 32 26 
 
2. Să se calculeze f ( A) , dacă:
 1 − 1
A =   ; f ( X ) = X 2 − 5X + 7I 2
 2 1

33. 2 1−  1−  −1 2
A = ⋅A=  ⋅ =  
2 1 2 1  4−1

34.  − 1 2  1 −   1 0
f(A)=  − 5 + 7 =
4 −1 2 1 0 1
 − 1 2  − 5   7 0
=  +  +  =
4 −1  10−− 5 0 7
 − 6 3   7 0
=  +  =
− 6  0 7

35.  1 1
3. Fie A =   . Să se calculeze A n , n ∈ N * .
 0 1
 1   1   1 2
A = A⋅ =  ⋅  =  
2
0 1 0 1 0 1

36. 23 1 2 1  1 3
A = A ⋅ =  ⋅  =  
0 1 0 1 0 1

 1 n
A =  
n
 0 1
Inducţie matematică P (k ) → P (k +1)
 1 n + 1
n+ 1
A =  
 0 1

37. nn+1 1 n 1  1 n+ 1
A = A ⋅ =  ⋅  =   (A)
0 1 0 1 0 1
 1 n
Deci A =  
n
.
 0 1
pg. 120 1. Calculaţi determinanţii de ordinul doi:
1−1
1) = 1⋅3− ( 1)⋅ =+= 5232
23

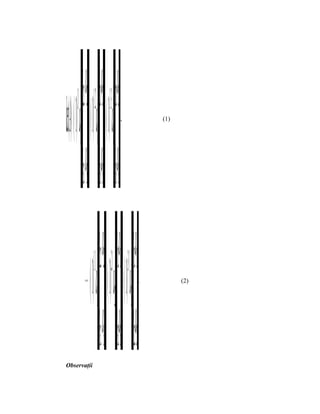
38. −1 1
2) (−= 1)⋅ ( 2)−− 1⋅ −= 323 = − 1
3−2
3)
31
()
= 3⋅ − 3 ( 3)⋅−− 1= 33 =+− 0
3 −− 3
2. Calculaţi determinanţii de ordinul trei:
2 −1 −2
6 − 1 1 = 2 ⋅ (− 1) ⋅ 3 + (− 1) ⋅ 1⋅ 4 + 6 ⋅ 5 ⋅ (− 2) − [ (− 2) ⋅ (− 1) ⋅ 4 + 2 ⋅ 1⋅ 5 + (− 1) ⋅ 6 ⋅ 3] =
1)
4 5 3
= −6 − 4 − 60 −[8 +10 −18] =
= −70
2 0−5
2) 5 3 3 = 2⋅3 6+ 0⋅3 0+ 5⋅ 4 ( 5) [(−−− 5)⋅3 0+ 2⋅3 4+ 0⋅5 6] =
046
= 36 + 0 −100 −[0 + 24 + 0] =
= −64 − 24 =
= −88

39. 1 2−3
3) 3 − 1 2 = 1⋅ (− 1)⋅1+ 2⋅ ( 2)+− 3⋅ ( 3) [(−−− 1)⋅ (− 2)⋅ ( 3)+− 1⋅ 2 3+ 1⋅ 2 3] =
−2 3 1
= −1 − 8 − 27 −[ −6 + 6 + 6] =
= −36 − 6 =
= −42
3. Calculaţi determinanţii următori:

40. a+ d b c+ d a b c d a b c 1
1)
a b c abc ab c abc+=+= dab =0+dc ⋅ =0
1 111 1 1

41. a+ b − a b − a b b a b b
2)
b+c −bc= −bc+ c= 1b c+− c=−1⋅0+ =
c+ a − c a − c a a c a a
4. Să se rezolve ecuaţiile:
1xx
1) x 1 x= 0
xx1

42. 11x 12x 1+++ 31 x 1
1⋅(−) +x1 +x⋅(−1) =0⇔ −x + =0⇔
x1 x 1 x
⇔ 1 − x 2 − x( x − x 2 ) + x( x 2 − x) = 0 ⇔ 1 − x 2 − x 2 + x 3 + x 3 − x 2 = 0 ⇔ 2 x 3 − 3 x 2 + 1 = 0 ⇔
⇔ 2 x 3 − 2 x 2 − x 2 + 1 = 0 ⇔ 2 x 2 ( x − 1) − ( x 2 − 1) = 0 ⇔ 2 x 2 ( x − 1) − ( x − 1)( x + 1) = 0 ⇒
⇒ ( x − 1)(2 x 2 − x − 1) = 0 ⇒ ( x − 1) = 0 ⇒ x1 = 1
⇒ 2 x 2 − x − 1 = 0 ⇒ ∆ = 1 + 8 = 9 ⇒ x2 = 1
1
⇒ x3 = −
2
 1 
Deci x ∈ − ,1 .
 2 

43. 5. Să se rezolve ecuaţiile:
011x
x 011
1) =0
1x01
11 x 0
01 x1 x01 x01
1+ 1+2 1+3 1+4
0⋅(−1) x01+ ⋅(−) 10 +1⋅(−) 1x + ⋅(−1) x0= ⇔
1x0 1x0 1 0 1 x

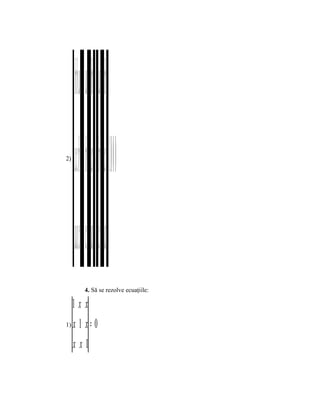
44. x 1 x 01 x 0 1
⇔ 0 101 1−+− xx 1 x 0= ⇔
1x0 1 0 1 x
⇔ 0 − [ ( x ⋅ 0 ⋅ 0 + 1 ⋅ 1 ⋅ 1 + 1 ⋅ x ⋅ 1) − (1 ⋅ 0 ⋅ 1 + 1 ⋅ 0 ⋅ 1 + x ⋅ 1 ⋅ x)] + [ x ⋅ 0 ⋅ x + 0 ⋅ 1 ⋅ 1 + 1 ⋅ 1 ⋅ 1 − (1 ⋅ x ⋅ 1 + 1 ⋅ x ⋅ 1 + 0 ⋅ 0 ⋅ 1)] −
− x[ ( x ⋅ x ⋅ x + 0 ⋅ 0 ⋅ 1 + 1 ⋅ 1 ⋅ 1) − (1 ⋅ x ⋅ 1 + 1 ⋅ 0 ⋅ x + 1 ⋅ 0 ⋅ x)] = 0 ⇔
⇔ −( x + 1 − x 2 ) + (1 − 2 x) − x ( x 3 + 1 − x) = 0 ⇔
⇔ x 2 − x − 1 − 2x + 1 − x 4 − x + x 2 = 0 ⇔
⇔ − x 4 + 2x 2 − 4x = 0 ⇔ x 4 − 2x 2 + 4 = 0 ⇔
⇔ x ( x 3 − 2 x + 4) = 0 ⇒ x1 = 0
⇒ x3 − 2x + 4 = 0
6. A, B ∈Μ 3 ( R)
Fie pentru care
det( A) = det( B ) = det( A + B) = det( A − B) = 0 . Să se arate că det( xA + yB) = 0 ,
(∀ x, y ∈R .
)
det( xA + yB ) = P ( x, y ) = λ1 x 3 + λ2 x 2 y + λ3 xy 2 + λ4 y 4 = 0
Pentru x = 0 şi y = 1
P (0,1) = det( B ) = 0 ⇒ λ4 = 0
Pentru x = 1 şi y = 0
P(1,0) = det( A) = 0 ⇒ λ1 = 0
Pentru x = 1 şi y = 1
P (1,1) = det( A + B ) = 0 ⇒ λ2 + λ3 = 0
Pentru x = 1 şi y = −1
P (1,−1) = det( A − B ) = 0 ⇒ λ2 − λ3 = 0
⇒ λ 2 = λ3 = 0
Deci det( xA + yB ) = 0

45. 2. Bacalaureat
pg. 94 1. Să se determine matricea X din ecuaţia
 2 − 3  1 3   − 3 6 
    
3X +  − 1 2  = ⋅  7 4  +  − 9 3
 2 − 3  − 2 6   3 0 
    

46.  2 6   − 3 6   2 − 3
   
3 X =  14 8  +  − 9 3  −  1 2 
 − 4 12   3 0   2 − 3 
   
 − 1 12   − 2 3 
  
3X =  5 1  +  1 − 2
 − 1 12   − 2 3 
  

47.  − 3 15   − 1 5
   
3X =  6 9 ⇒ X =  2 3 
 − 3 15   − 1 5
   
2. a) Găsiţi matricea X ∈ Μ 2 ( R ) astfel încât
 1 2   − 2 1  1 2 
X +  =  
0 1  3−  31
b) Să se determine m∈ R astfel încât sistemul următor să fie compatibil
şi apoi rezolvaţi-l:
x+ y = 1

 x − 2y = − 1
 3x + y = m


48.  1 2   − 2 1  1 2 
a)
X +  =  
0 1  3 −  31

49.  1 2  − 1  2  − 1
⇒= − ⇒XX  = + ⇒
013 − 013−

50. 12 31
⇒ X = 
0 1 04 x⋅1+y0x⋅2+y1 31  x2+y 31
⇒  = ⇔  = ⇒
x y 2⋅z+t0 z⋅2+t1 04 2z +t 04
X= 
zt


51. x= 3
 2z = 0 ⇒ z = 0

⇒
 2x + y = 1 ⇒ 6 + y = 1 ⇒ y = − 5
 2z + t = 4 ⇒ t = 4

 3 − 5
Deci X =   .
 0 4
x+ y = 1

b)  x − 2 y = − 1
 3x + y = m

x + y =1 ⇒ x =1 − y
2
x − 2 y = −1 ⇒ 1 − y − 2 y = −1 ⇒ −3 y = −2 ⇒ y =
3
2 1
x =1− y =1−
⇒x=
3 3
1 2 2 5
3x + y = m ⇒ 3 ⋅ + = m ⇒ m = 1 + ⇒ m =
3 3 3 3
 1 a
3. a) Fie matricea A ∈ Μ 2 ( R ) ; A =   , a ≠ 0 . Să se calculeze A 2 şi A 3
 0 1
şi apoi să se determine A n , n ∈ N * în funcţie de n.
b) Să se afle x, y, u , v, numere reale astfel încât

52.  1  x y  1 0
  = 
0 1 uv 1 

53. 2 1  1aa  1⋅ +a0 ⋅1+a  12a
a)
A= ⋅A  ⋅ = = 
0 1 01 0⋅1+ 1⋅ +0a 0 1

54. 23 12 1aa  1⋅ +2a⋅0 1+2aa ⋅1  3a
A= ⋅A= ⋅ = = 
0 1 01  0⋅1+ 1⋅ +0a 0 1

 1 na
A =  
n
 0 1
Inducţie matematică P (k ) → P (k +1)

55.  1 (n + 1)a
n+ 1
A =  
 0 1
+1 nn 1 a1an 1⋅+na0 ⋅1+na  1(n+ )a
A = ⋅A= ⋅ = =  (A)
0 10  0⋅1+ 1⋅+0a 0 1
1 na 
Deci A = 
 0 1 .
n

 

56.  x + u = 1⇒ x 0
y11 xy 0 x+u v 10 y+v= ⇒ y−10
     
b)
  = ⇒  = ⇒ 
0 1uv 1   u v 1 u=1
v=1

57.  x y   0 − 1
Deci
  =   .
u v  1 1
4. a) Să se determine x, y, u , v, astfel încât:
 − x y  xy  − 31
 −  =  
+ 1vu  3 1− 2uv  − 8 2
b) Să se detrmine matricea A astfel încât:

58. 410−5 7−1  1 5 2
2A+ =  + .
6 12−3 12 15 4214

59.  − x y  − 3 1  x y  −  3 1
a)
 − = ⇔ + = ⇔
u+1v3−2u8 +1v−32u 8

60.  (x+− y)= 3⇒− x y =+ 3
 xy =− 1
 x−− y − xy   − 3 1 
⇔   =   ⇒ 
 u −+ 31 vv + 2u− 1  − 8 2  u 3v+− 1= − 8
 2u v 1=−+ 2
 = 3− yx  = 3− yx 2y= 4 y= 2
⇒ ⇔ ⇔ ⇔
y − x= 1 y+ − 3=1  = 3− yx x= 1
 u− 3v+ 1= − 8  u = 3v− 9  v= 3
⇒ ⇔ ⇔
 2u v 1=−+ 2  2(3v 9) v 3⇒=+− 7v= 21  u = 0

61. 410−5 7−1  1 5 2
b)
2A+ = + 
6 12−3 12 15 4214
8413 0−5 8413− 105
⇒2A= − ⇒2A= + ⇔
162 9612−3 162 9−6123

62.  4 − 6 18   2 − 3 9 
2A=⇔   A=⇒   .
1 0 10 2  5 5 1 
pg. 147 1. Să se rezolve ecuaţia:
xaaa
axaa
=0
aaxa
aaax

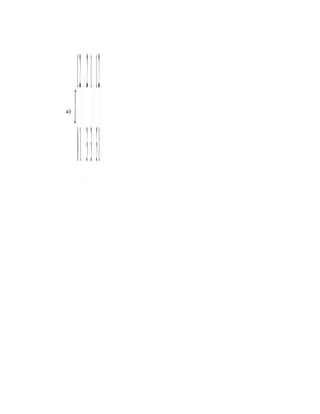
63. x a x− a 0 0 0 a a x− a 0 0 0
a x a 0 x− a 0 0 a a 0 x− a 0 0
= 0⇔ + = 0⇔ = 0⇔
a x a 0 0 x− a 0 a a 0 0 x− a 0
a x 0 0 0 x− a a a 0 0 0 x− a
− ax 0 0
[]
⇔ ( − ax )⋅ (− 1)1+ 0 − ax 0 0⇒= ( − )( − axax )3 0 0⇒=− ( − ax )4 0⇒= x1,23,4 = a
0 0 − ax

64. 2. Dacă x1 , x 2 , x3 sunt rădăcinile ecuaţiei x 3 − 2 x 2 + 2 x + 17 = 0 să se
x1 x2 x3
calculeze determinantul d = x2 x3 x1 .
x3 x1 x2
 x1 + x2 + x3 = 2

x3 − 2x 2 + 2x + 17 = 0 ⇒  x1x2 + x1x3 + x2 x3 = 2
 x x x = − 17
 123
x1 x2 x3
3 3 3
x x x = 3 xxx − (x + x + x )
2 3 1 123 1 2 3
x3 x1 x2
3 2
x1 − 2 x1 + 2 x1 + 17 = 0
3 2
x2 − 2 x2 + 2 x 2 + 17 = 0
3 2
x3 − 2 x3 + 2 x3 + 17 = 0 (+ )
x1 + x 2 + x3 = 2( x1 + x 2 + x3 ) − 2( x1 + x 2 + x3 ) − 51
3 3 3 2 2 2
 3 3 3
 ⇒ x1 + x 2 + x3 = 2(2 − 2) − 2 ⋅ 2 − 51 ⇒
x1 + x 2 + x3 = ( x1 + x2 + x3 ) 2 − 2( x1 x 2 + x1 x3 + x 2 x3 ) 
2 2 2

3 3 3
⇒ x1 + x 2 + x3 = − 55
3 3 3
d = 3 x1 x 2 x3 − ( x1 + x 2 + x3 ) = 3 ⋅ ( −17) + 55 ⇒ d = 4
Siruri marginite
Definitii:
1.Spunem ca sirul ( Xn)n este margin sup(majorat)⇔ (∃ ) b∈ R a.i
Xn ≤ b, (∀ ) n.
2.Spunem ca sirul ( Xn)n este margin inf (minorat ) ⇔ (∃ ) a∈ R a.i
a ≤ Xn, (∀) n .

65. 3.Spunem ca sirul (Xn)n este marginit ⇔ este si majorat si minorat
(∃ ) a,b ∈ R a.i a ≤ Xn ≤ b (∀) n.
Prop. Sirul (Xn) n este marginit ⇔ (∃) M∈R a.i Xn ≤ M, ( ∀) n
! Obs. (Xn) ≤ M ⇔ -M ≤ Xn ≤ M.
Siruri monotone
Definitie: Spunem ca sirul Xn este:
a) strict crescator ⇔ Xn < Xn+1 <….
X0 < X1<X2……< Xn < Xn+1 <….
b) strict descrescator daca Xn >Xn+1, (∀ )n≥ 0
c) crescator daca Xn ≤ Xn+1 (∀) n ≥ 0
X0 ≤ X1 …….≤ Xn ≤ Xn+1≤ ……
d) descrescator daca Xn ≥ Xn+n ,(∀) n≥0
X0≥X1≥X2….≥Xn≥ Xn+1≥….
Ex: (Xn): 1,1,2,2,…….n,n…..sir crescator
(Yn): 1,2,3….n,n+1….strict crescator
(Zn): 1,1,1/2,1/2,1/3,1/3….descrescator
(Rn): -1,-2,-3……-n, strict descrescator
!Obs. ∗Un sir crescator este marginit inf de primul termen Xo
∗Un sir care este crescator sau descrescator (respectiv strict) se
numeste monoton (respective strict monoton)
Pentru a stabili monotonia unui sir se face diferenta a doi termeni a Z
termeni oarecare consecutivi si aceasta se compara cu 0.
Daca termenii sirului este pozitiva se face raportul a doi termeni
consecutivi oarecare si se compara cu unu

67. www.eReferate.ro -Cea mai buna inspiratie…

68. SIRURI FUNDAMENTALE
( SIRURI COUCHY )
Definitia 1:
Spunem ca un sir an este fundamental (sau sir Couchy) daca
( ∀)ε > 0, ( ∃) N = N ( ε ) astfel incat an − am < ε , ( ∀) n, m ≥ N ( ε ).
Definitia 2:
Spunem ca un sir an este fundamental (sau sir Couchy) daca
( ∀)ε > 0, ( ∃) N = N ( ε ) astfel incat an+p − an < ε , ( ∀) n ≥ N ( ε ) si p ∈N ∗.
Definitia 3:
Spunem ca un sir an este fundamental (sau sir Couchy) daca
( ∀)ε > 0, ( ∃) N = N ( ε ) astfel incat an − a N < ε , ( ∀) n ≥ N ( ε ) .
Observtie!
Cele trei definitii date sunt echivalente:
Defintia 1 ⇔ Definitia 2 ⇔ Definitia3
Criteriul lui Couchy:
Un sir de numere reale este convergent daca si numai daca este sir Couchy.
Problem propuse spre rezolvare:
( an ) sir fundamental ⇔ ( an ) este convergent
I. Utilizand criteriul lui Couchy sa se arate ca urmatoarele siruri sunt convergente:
Rezolvare:
2n +1
1) an =
5n + 2
Demonstram ca
( ∀)εp > 0,n( ∃) N ( =+ pε +astfel n + 1 = n+p −an
an + − a =
2 n N ( ) ) 1 2 incat a
− < ε , ( ∀ n ≥ N (ε ) si p ∈N ∗
)
5( n + p ) + 2 5n + 2
=
( 5n + 2 )( 2n + 2 p + 1) − ( 2n + 1)( 5n + 5 p + 2 ) =
( 5n + 2 )( 5n + 5 p + 2 )
10n 2 + 10np + 9n + 4 p + 2 −10n 2 −10np − 9n − 5 p − 2
= =
( 5n + 2 )( 5n + 5 p + 2 )
p p
= n + p − an < ε ⇒
a <ε
( 5n + 2 )( 5n + 5 p( 5n2+ 2 )( 5n + 5 p + 2)
+ )

69. ( ∀)ε > 0, ( ∃) N = 1 + 1 −10ε  astfel incat
  an + p − an < ε , ( ∀) n ≥ N ( ε ) si p ∈ N
 25ε 
n
sin k 2
3) cn = ∑ k 1 1 1 1
2) b = 1 +
n
k =1 2
+ 2 + 3 ++ n
n+ p
2 2 2 2 n+p n+p
sin k 2 n
sin k 2 sin k 2 sin k 2
cn + p − cn = ∑
k =1 2k
−∑ k =
k =1 2
∑
k =n +1 2k
≤ ∑
k =n +1 2k
≤
Demonstram ca 
n+p
1 1 1 1  1
≤
k
∑ = 1 + + + <
) n 1 0 2 =  astfel incatp −1n+p −2n <ε , ( ∀)n ≥ N (ε ) si p ∈N
( ∀=ε+>2 k, ( ∃) Nn +1 N (ε ) 2
 2 b  bn
dupa cum am aratat la exercitiul anterior ⇒
 1
⇒se obtine N ( ε ) =1 + log 2 
 ε
1 1 1 1 1 1 1 1
bn + − n = + + 2 + + n
p b 1  + n+ + + n+ − − − 2 − − n =
1
 p
1 
2 2 2 2 2 2 2 2
1 1 1 1  1 1  1 1 1 1 
= n+ + n+ + + n+ = n+
  + + + p− 
1  < n  + 2 + + p =

2 1 2 2 2 p 2 1  2 2 1
 2  2 2 2 
1  1 
 − p
1  n
1 2  2 cos k!
= 1  − 1  1
4) d = ∑
= n ⋅ n 
1 p 
< n
2 1 2  2  2
p este un numar(arbirar.Cind p → ∞ obtinem :
k k +1)
1− n
2 k= 1
1 
bn + − n < n 
b 1 1
⇒
p
2  ⇒n ≤ ⇒ >p ε n log 2 p 1
ε
lim
bn + − n <
b ε  2 n +p = lim =
( 5n +d2)( 5n + 5 p + 2) k! − ( cosk! = n2 p cosn + 2)≤
 +
( k!
p
n
cos
∑k ( k  1) k =n +1 k (5k5+1)
5n
p →∞ p →∞
d 
Deci N (ε = + p  −
) 1 + logn  1 =∑ p 5n + 2)  + 5 +∑ 
k ( k +1) p
n

2
ε k =1
 +
k= 1  p 
n +p n +p n +p
1 cos k1 −10ε
! 1 1 −10ε  1 1
⇒
∑ k ( k +1)
k =n +1
∑ k ( k −1)
≤5( 5n + 2) ≤ ε ⇒ n ≥ 25ε<, deci putem lua N ( ε ) = 1= 25ε 
k =n +1
+
  ∑k
k =n +1
−
k −1
=
1 1 1
(=ε > 0, ( ∃) N−) = 1 + log 2 1  astfel incat bn + p − bn
∀) (ε  ε  < < ε , ( ∀) n ≥ N ( ε ) si p ∈ N
n +1 n + p +1 n +1
( ∀)ε > 0, ( ∃) N ( ε ) = 1 + log 2 1 1  bn + p − bn
< ε , ( ∀) n ≥ N ( ε ) si p ∈ N
d n + p −d n  < ε   1  astfel incat
1 −ε 
⇒ n +1 ⇒ ≤ ε ⇒N (ε ) =1 + 

d n + p −d n < ε 
n +1  ε  

70. II. Aratati ca urmatorul sir de numere reale nu este fundamental:
1 1 1
xn = 1 + + ++
2 3 n
Aratam ca :
( ∃)ε > 0, ( ∀) N = N ( ε ) astfel incat xn + p − xn ≥ ε , ( ∀) n ≥ N ( ε ) si p ∈ N ∗
2n n 2n 2n 2n
1 1 1 1 1 1 1 1
x2 n − xn = ∑k − ∑k
k=1 k=1
= ∑k
k =n +1
≤ ∑
k =n +1 k
= ∑ =
k =n +1 k
+
n +1 n + 2
+ +
2n
>
1 1 1 1 1
> + + + =n =
2n 2n 2n 2n 2
1
x2 n − xn > ⇒
2
1
⇒ ( ∃)ε = , ( ∀) N = N ( ε ) astfel incat xn + p − xn ≥ ε, ( ∀) n ≥ N ( ε )
3
⇒ sirul xn nu este fundamental
LIMITA FUNCTIEI LOGARITMICE
LIMITA FUNCTIEI LOGARITMICE

71. LIMITA FUNCTIEI
TRIGONOMETRICE DIRECTE
• Daca punctual de acumulare este finit adica a∈R atunci
Deci limita functiei sinus intr-un punct de acumulare finit a∈R se
obtine inlocuind pe x cu a
• Daca a= ±∞ atunci f nu are limita
• Daca punctual de acumulare este finit adica, a∈R atunci
Deci limita functiei cosinus intr-un punct de acumulare finit a∈R se
obtine inlocuind pe x cu a
• Daca a apartine domeniului de definitie atunci :

72. Se poate lua :
Deci limita functie tangenta intr-un punct de acumulare din domeniul
de definitie se obtine inlocuind pe x cu a
Deci limita functiei cotangenta intr-un punct de acumulare din domeniul de
def se obtine inlocuind pe x cu a
LIMITELE FUNCTIILOR
TRIGONOMETRICE INVERSE
Se demonstreaza ca daca a ∈[-1,1] atunci
OBSERVATIE :Pentru toate functiile elementare , limita functiei in orice punct al
multimii de definitie a , se obtine inlocuind pe x cu a .

73. OPERATII CU LIMITE DE FUNCTII
LIMITE REMARCABILE
1.
2.
3.
4.
5.

74. 6.
7.
8.
LIMITA FUNCTIEI
TRIGONOMETRICE DIRECTE
• Daca punctual de acumulare este finit adica a∈R atunci
Deci limita functiei sinus intr-un punct de acumulare finit a∈R se
obtine inlocuind pe x cu a
• Daca a= ±∞ atunci f nu are limita
• Daca punctual de acumulare este finit adica, a∈R atunci
Deci limita functiei cosinus intr-un punct de acumulare finit a∈R se
obtine inlocuind pe x cu a
• Daca a apartine domeniului de definitie atunci :

75. Se poate lua :
Deci limita functie tangenta intr-un punct de acumulare din domeniul
de definitie se obtine inlocuind pe x cu a
Deci limita functiei cotangenta intr-un punct de acumulare din domeniul de
def se obtine inlocuind pe x cu a
LIMITELE FUNCTIILOR
TRIGONOMETRICE INVERSE
Se demonstreaza ca daca a ∈[-1,1] atunci
OBSERVATIE :Pentru toate functiile elementare , limita functiei in orice punct al
multimii de definitie a , se obtine inlocuind pe x cu a .

76. OPERATII CU LIMITE DE FUNCTII
LIMITE REMARCABILE
1.
2.
3.
9.
10.

77. 11.
12.
13.

78. CUPRINS
1.Matrici......
…………………………………………..pag3 *despre matrici
*operatii cu matrici
*propietatii
*teorema lui Hamilton
2.Determinanti ..........................................pag7
*definitii
*regula triunghiului
*calculul inversei unei matrici
*ecuatii matriciale
3.Sisteme de ecuatii liniare.........................pag 14
*metoda reducerii
*metoda substitutiei
*formulele lui CRAMER
*metoda lui GAUSS
4.Chestiuni elementare despre siruri ...........pag13
*siruri de numere reale
*operatii cu limite si siruri
5.Limite de functii........................................pag17
*limita functiei logaritmice
*limita functiei trig directe
*operatii cu limite
*limite remarcabile
*limita functiei trig inverse