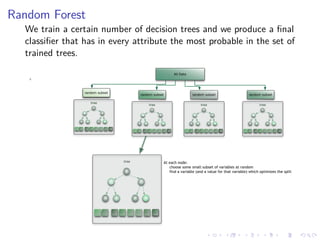
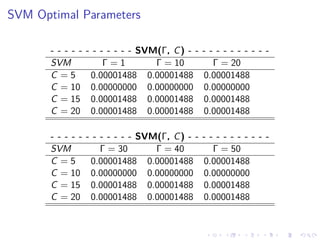
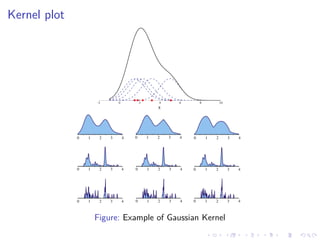
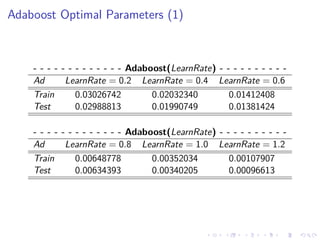
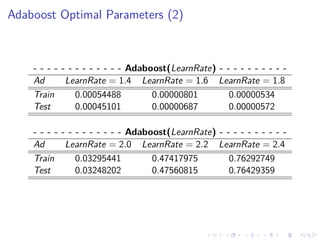
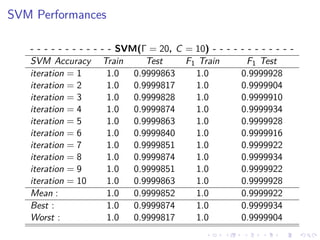
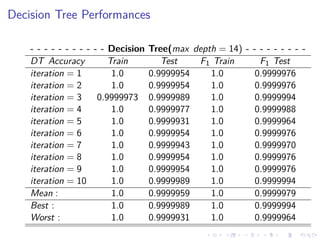
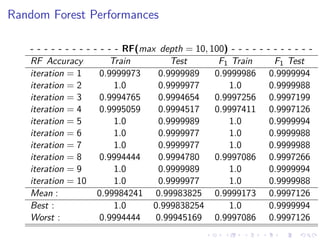
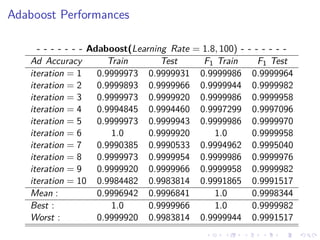
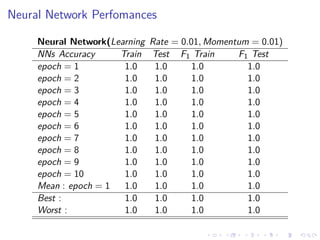
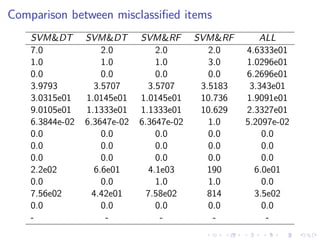
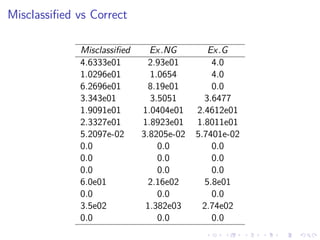
This document summarizes the results of a study on classifying tables in HTML documents as genuine or non-genuine tables. It describes the dataset, features considered for the classification including layout, content type and word group features. It discusses various machine learning models tested - SVM, Decision Tree, Random Forest, Adaboost and Neural Networks. It provides the optimal parameters determined for each model and compares their performance on the table classification task based on accuracy, F1 score and confusion matrices.

1. Web algorithm Project
Armenise Iolanda
Cataldi Alessandro
Filingeri Giuseppe
13 Ottobre 2016
Dott. Perehodko Eugeniya
Prof. Italiano Giuseppe

2. Problem: Table Detection
To recognize genuine and non genuine tables from HTML pages.
Genuine tables: entities where a structure is used to convey
the logical relations among the cells.
Non-genuine tables: entities where <TABLE> tags are used
to group contents into clusters for easy viewing only.

3. Problem: Table Detection
Our dataset was composed by 1393 HTML pages, collected by
Yalin Wang and Jianying Hu.
Figure: Example of genuine table & non genuine table

4. Features
We consider fourteen features divided in three different groups:
Layout Features
Content Type Features
Word Group Features

5. Layout Features
Group composed by six features
Average number of columns
Standard deviation of number of columns
Average number of rows
Average overall cell length
Standard deviation of cell length
Average Cumulative length consistency

6. Content Type Features
We define the set of content types
T = {Image, Form, Hyperlink, Alphabetical and Digit, Empty, Others}
This group of features includes six components of the histogram
made by the distribution of content type in a table
In addition we have the average content type consistency

7. Word Group Features
The word feature is the ratio between the impact of genuine vector
on the test vector and the impact of the non genuine one on the
same test vector. These vectors are computed with the following
informations:
Genuine counter for each word
Non-genuine counter for each word
Frequency in genuine tables
Frequency in non-genuine tables
Frequency in a new test table

8. Machine Learning Methods
We consider the following Machine Learning Model
Support Vector Machine (SVM)
Decision Tree (DT)
Random Forest (RF)
Adaptive Boosting (Adaboost)
Neural Networks (NNs)

9. Support Vector Machine
Given a set of labeled points T = {(xi , yi ) |i = 1, . . . , m} we
investigate the hyperplane H : wT x + b = 0 such that
wT xi + b ≥ 1 ∀xi ∈ A
wT xj + b ≤ −1 ∀xj ∈ B
where A is the set of positive items and B the negative ones.
This problem requires the solution of an optimization problem in
order to find w ∈ Rn and b ∈ R such that
the margin of H wrt T is maximized.
construct the decision function f (x) = sgn(wT x + b)

10. Decision Tree
Decision trees classify instances by sorting them from the root to
some leaf node, which provides the classification of the instance.
Choose the attribute which minimizes the impurity:
K
i=1
2pi (1 − pi ) Gini index
Partition the training set according to all the possible values
of the above attribute
Apply the same procedure for the remaining attributes and
instances.

11. Random Forest
We train a certain number of decision trees and we produce a final
classifier that has in every attribute the most probable in the set of
trained trees.

12. Adaboost

13. Neural Networks
Let X ⊆ RM×D be the set of elements in the Dataset, we build a
decision function
y(x, w) = f


M
j=1
wjφj(x)


and train parameters as in the following rules:
a
(1)
j =
d
i=1
w
(1)
ji xi + w
(1)
j0
z
(1)
j = h1(a
(1)
j )
σ(x) =
1
1 + e−x
z
(r)
j = hr (a
(r)
j )

14. Pseudocode: Features Creation
Read HTML pages from folder
Transform HTML to txt
Detect table starttag and endtag
Detect row startag and endtag
Detect cell startag and endtag
Detect data inbetween
Create features
Print features in txt

15. Pseudocode: Machine Learning
read data from txt
divide features from label
split dataset for cross validation
train Algorithms
predict test set
print performances

16. Metrics
Precision
The percentage of instances the classifier labeled positive that
are actually positive
#TruePositive
#TruePositive + #FalsePositive
Recall
The percentage of positive instances that the classifier labeled
as positive
#TruePositive
#TruePositive + #FalseNegative

17. Accuracy
The ratio between the number of correct classification over
the number of classification
#CorrectClassifications
#Classifications
F1-measure:
is the harmonic mean of precision and recall
2(Precision)(Recall)
Precision + Recall

18. SVM Optimal Parameters
- - - - - - - - - - - - SVM(Γ, C) - - - - - - - - - - - -
SVM Γ = 1 Γ = 10 Γ = 20
C = 5 0.00001488 0.00001488 0.00001488
C = 10 0.00000000 0.00000000 0.00000000
C = 15 0.00001488 0.00001488 0.00001488
C = 20 0.00001488 0.00001488 0.00001488
- - - - - - - - - - - - SVM(Γ, C) - - - - - - - - - - - -
SVM Γ = 30 Γ = 40 Γ = 50
C = 5 0.00001488 0.00001488 0.00001488
C = 10 0.00000000 0.00000000 0.00000000
C = 15 0.00001488 0.00001488 0.00001488
C = 20 0.00001488 0.00001488 0.00001488

19. Kernel plot
Figure: Example of Gaussian Kernel

20. Decision Tree Optimal Parameters
- - - - - - - - - - - - - Tree(depth) - - - - - - - - - - - - - -
DT depth = 3 depth = 5 depth = 8 depth = 12
Train 0.02978931 0.01694997 0.00527249 0.00109510
Test 0.02911431 0.01656725 0.00508934 0.00103824
- - - - - - - - - - - - - Tree(depth) - - - - - - - - - - - - - -
DT depth = 14 depth = 15 depth = 16 depth = 18
Train 0.00000267 0.00000000 0.00000000 0.00000000
Test 0.00000229 0.00000229 0.00000343 0.00000572

21. Random Forest Optimal Parameters
- - - - - - Random Forest(Numb.Tree,depth) - - - - - -
RF depth = 9 depth = 10 depth = 11 depth = 12
Train 0.0013168 0.0000027 0.0000000 0.0000000
Test 0.0013118 0.0000011 0.0000011 0.0000011
- - - - - - Random Forest(Numb.Tree,depth) - - - - - -
RF depth = 13 depth = 14 depth = 15 depth = 16
Train 0.0000000 0.0000000 0.0000000 0.0000000
Test 0.0000011 0.0000011 0.0000011 0.0000011

22. Adaboost Optimal Parameters (1)
- - - - - - - - - - - - - Adaboost(LearnRate) - - - - - - - - - -
Ad LearnRate = 0.2 LearnRate = 0.4 LearnRate = 0.6
Train 0.03026742 0.02032340 0.01412408
Test 0.02988813 0.01990749 0.01381424
- - - - - - - - - - - - - Adaboost(LearnRate) - - - - - - - - - -
Ad LearnRate = 0.8 LearnRate = 1.0 LearnRate = 1.2
Train 0.00648778 0.00352034 0.00107907
Test 0.00634393 0.00340205 0.00096613

23. Adaboost Optimal Parameters (2)
- - - - - - - - - - - - - Adaboost(LearnRate) - - - - - - - - - -
Ad LearnRate = 1.4 LearnRate = 1.6 LearnRate = 1.8
Train 0.00054488 0.00000801 0.00000534
Test 0.00045101 0.00000687 0.00000572
- - - - - - - - - - - - - Adaboost(LearnRate) - - - - - - - - - -
Ad LearnRate = 2.0 LearnRate = 2.2 LearnRate = 2.4
Train 0.03295441 0.47417975 0.76292749
Test 0.03248202 0.47560815 0.76429359

24. Neural Networks Optimal Parameters
- - - - - - - - Neural Network(LearnRate,Momentum) - - - - - -
NN LearnRate = 1 LearnRate = 0.1 LearnRate = 0.01
M = 1 0.0 0.0 0.0
M = 0.1 0.0 0.0 0.0
M = 0.01 0.0 0.0 0.0

25. SVM Performances
- - - - - - - - - - - - SVM(Γ = 20, C = 10) - - - - - - - - - - - -
SVM Accuracy Train Test F1 Train F1 Test
iteration = 1 1.0 0.9999863 1.0 0.9999928
iteration = 2 1.0 0.9999817 1.0 0.9999904
iteration = 3 1.0 0.9999828 1.0 0.9999910
iteration = 4 1.0 0.9999874 1.0 0.9999934
iteration = 5 1.0 0.9999863 1.0 0.9999928
iteration = 6 1.0 0.9999840 1.0 0.9999916
iteration = 7 1.0 0.9999851 1.0 0.9999922
iteration = 8 1.0 0.9999874 1.0 0.9999934
iteration = 9 1.0 0.9999851 1.0 0.9999922
iteration = 10 1.0 0.9999863 1.0 0.9999928
Mean : 1.0 0.9999852 1.0 0.9999922
Best : 1.0 0.9999874 1.0 0.9999934
Worst : 1.0 0.9999817 1.0 0.9999904

26. SVM Confusion Matrices
Here we present the confusion matrices for the best and worst
cases in ten iterations
- - SVM(Γ = 20, C = 10) - -
Best Case
40359 0
11 833221
- - SVM(Γ = 20, C = 10) - -
Worst Case
40460 0
16 833115

27. Decision Tree Performances
- - - - - - - - - - - Decision Tree(max depth = 14) - - - - - - - - -
DT Accuracy Train Test F1 Train F1 Test
iteration = 1 1.0 0.9999954 1.0 0.9999976
iteration = 2 1.0 0.9999954 1.0 0.9999976
iteration = 3 0.9999973 0.9999989 1.0 0.9999994
iteration = 4 1.0 0.9999977 1.0 0.9999988
iteration = 5 1.0 0.9999931 1.0 0.9999964
iteration = 6 1.0 0.9999954 1.0 0.9999976
iteration = 7 1.0 0.9999943 1.0 0.9999970
iteration = 8 1.0 0.9999954 1.0 0.9999976
iteration = 9 1.0 0.9999954 1.0 0.9999976
iteration = 10 1.0 0.9999989 1.0 0.9999994
Mean : 1.0 0.9999959 1.0 0.9999979
Best : 1.0 0.9999989 1.0 0.9999994
Worst : 1.0 0.9999931 1.0 0.9999964

28. Decision Tree Confusion Matrices
Here we present the confusion matrices for the best and worst
cases in ten iterations
Decision Tree(max depth = 14)
Best Case
40505 0
1 833085
Decision Tree(max depth = 14)
Worst Case
40335 1
5 833250

29. Random Forest Performances
- - - - - - - - - - - - - RF(max depth = 10, 100) - - - - - - - - - - - -
RF Accuracy Train Test F1 Train F1 Test
iteration = 1 0.9999973 0.9999989 0.9999986 0.9999994
iteration = 2 1.0 0.9999977 1.0 0.9999988
iteration = 3 0.9994765 0.9994654 0.9997256 0.9997199
iteration = 4 0.9995059 0.9994517 0.9997411 0.9997126
iteration = 5 1.0 0.9999989 1.0 0.9999994
iteration = 6 1.0 0.9999977 1.0 0.9999988
iteration = 7 1.0 0.9999977 1.0 0.9999988
iteration = 8 0.9994444 0.9994780 0.9997086 0.9997266
iteration = 9 1.0 0.9999989 1.0 0.9999994
iteration = 10 1.0 0.9999977 1.0 0.9999988
Mean : 0.99984241 0.99983825 0.9999173 0.9997126
Best : 1.0 0.999838254 1.0 0.9999994
Worst : 0.9994444 0.99945169 0.9997086 0.9997126

30. Random Forest Confusion Matrices
Here we present the confusion matrices for the best and worst
cases in ten iterations
- RF(max depth = 10, 100) -
Best Case
40409 0
2 833180
- RF(max depth = 10, 100) -
Worst Case
39919 0
479 833193

31. Adaboost Performances
- - - - - - - Adaboost(Learning Rate = 1.8, 100) - - - - - - -
Ad Accuracy Train Test F1 Train F1 Test
iteration = 1 0.9999973 0.9999931 0.9999986 0.9999964
iteration = 2 0.9999893 0.9999966 0.9999944 0.9999982
iteration = 3 0.9999973 0.9999920 0.9999986 0.9999958
iteration = 4 0.9994845 0.9994460 0.9997299 0.9997096
iteration = 5 0.9999973 0.9999943 0.9999986 0.9999970
iteration = 6 1.0 0.9999920 1.0 0.9999958
iteration = 7 0.9990385 0.9990533 0.9994962 0.9995040
iteration = 8 0.9999973 0.9999954 0.9999986 0.9999976
iteration = 9 0.9999920 0.9999966 0.9999958 0.9999982
iteration = 10 0.9984482 0.9983814 0.9991865 0.9991517
Mean : 0.9996942 0.9996841 1.0 0.9998344
Best : 1.0 0.9999966 1.0 0.9999982
Worst : 0.9999920 0.9983814 0.9999944 0.9991517

32. Adaboost Confuson Matrices
Here we present the confusion matrices for the best and worst
cases in ten iterations
Adaboost(Learning Rate = 1.8, 100)
Best Case
40308 1
2 833280
Adaboost(Learning Rate = 1.8, 100)
Worst Case
39421 527
887 832756

33. Neural Network Perfomances
Neural Network(Learning Rate = 0.01, Momentum = 0.01)
NNs Accuracy Train Test F1 Train F1 Test
epoch = 1 1.0 1.0 1.0 1.0
epoch = 2 1.0 1.0 1.0 1.0
epoch = 3 1.0 1.0 1.0 1.0
epoch = 4 1.0 1.0 1.0 1.0
epoch = 5 1.0 1.0 1.0 1.0
epoch = 6 1.0 1.0 1.0 1.0
epoch = 7 1.0 1.0 1.0 1.0
epoch = 8 1.0 1.0 1.0 1.0
epoch = 9 1.0 1.0 1.0 1.0
epoch = 10 1.0 1.0 1.0 1.0
Mean : epoch = 1 1.0 1.0 1.0 1.0
Best : 1.0 1.0 1.0 1.0
Worst : 1.0 1.0 1.0 1.0

34. Neural Network Confusion Matrices
Here we present the confusion matrices for the best and worst
cases in ten iterations
NNs(Learning Rate = 0.01, Momentum = 0.01)
Best Case
40286 0
0 833305
NNs(Learning Rate = 0.01, Momentum = 0.01)
Worst Case
40425 0
0 833166

35. Tables Misclassified
Here we report the indices of the misclassified tables fixing a seed
as the third parameter of the sklearn cross validation equal to 123
SVM
{55805, 62727, 179529, 223217, 347970, 358230, 378442,
667878, 745882,789134}
Decision Tree {55805, 347970, 358230, 823020}
Random Forest {358230}
Adaboost {358230, 378442, 789134}

36. Confusion Matrices
SVM(Γ = 20, 10)
40320 0
10 833261
—RF(500,10)—
40329 0
1 833261
Adaboost(1.8, 100)
40327 0
3 833261
DT(depth = 14)
40327 1
3 833260

37. Comparison between misclassified items
SVM&DT SVM&DT SVM&RF SVM&RF ALL
7.0 2.0 2.0 2.0 4.6333e01
1.0 1.0 1.0 3.0 1.0296e01
0.0 0.0 0.0 0.0 6.2696e01
3.9793 3.5707 3.5707 3.5183 3.343e01
3.0315e01 1.0145e01 1.0145e01 10.736 1.9091e01
9.0105e01 1.1333e01 1.1333e01 10.629 2.3327e01
6.3844e-02 6.3647e-02 6.3647e-02 1.0 5.2097e-02
0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0
2.2e02 6.6e01 4.1e03 190 6.0e01
0.0 0.0 1.0 1.0 0.0
7.56e02 4.42e01 7.58e02 814 3.5e02
0.0 0.0 0.0 0.0 0.0
- - - - -

38. Misclassified vs Correct
Misclassified Ex.NG Ex.G
4.6333e01 2.93e01 4.0
1.0296e01 1.0654 4.0
6.2696e01 8.19e01 0.0
3.343e01 3.5051 3.6477
1.9091e01 1.0404e01 2.4612e01
2.3327e01 1.8923e01 1.8011e01
5.2097e-02 3.8205e-02 5.7401e-02
0.0 0.0 0.0
0.0 0.0 0.0
0.0 0.0 0.0
6.0e01 2.16e02 5.8e01
0.0 0.0 0.0
3.5e02 1.382e03 2.74e02
0.0 0.0 0.0

39. Conclusion
From the above results we may state that every classifier achieve
almost perfect results, since the number of misclassified items is
negligible with respect to the whole dataset.
Moreover the small number of misclassified element is so poor that
a link between them can not be found.