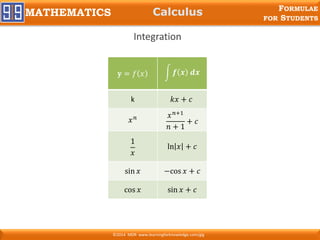
This document provides a collection of mathematical formulae for school students covering topics like algebra, trigonometry, analytical geometry, arithmetic, and complex numbers. It includes common formulae for indices, logarithms, quadratic equations, binomial expansion, trigonometric ratios and identities, lines and their equations, arithmetic and geometric series, and triangle properties. The formulae are presented without explanation, intended as a quick reference guide for students.