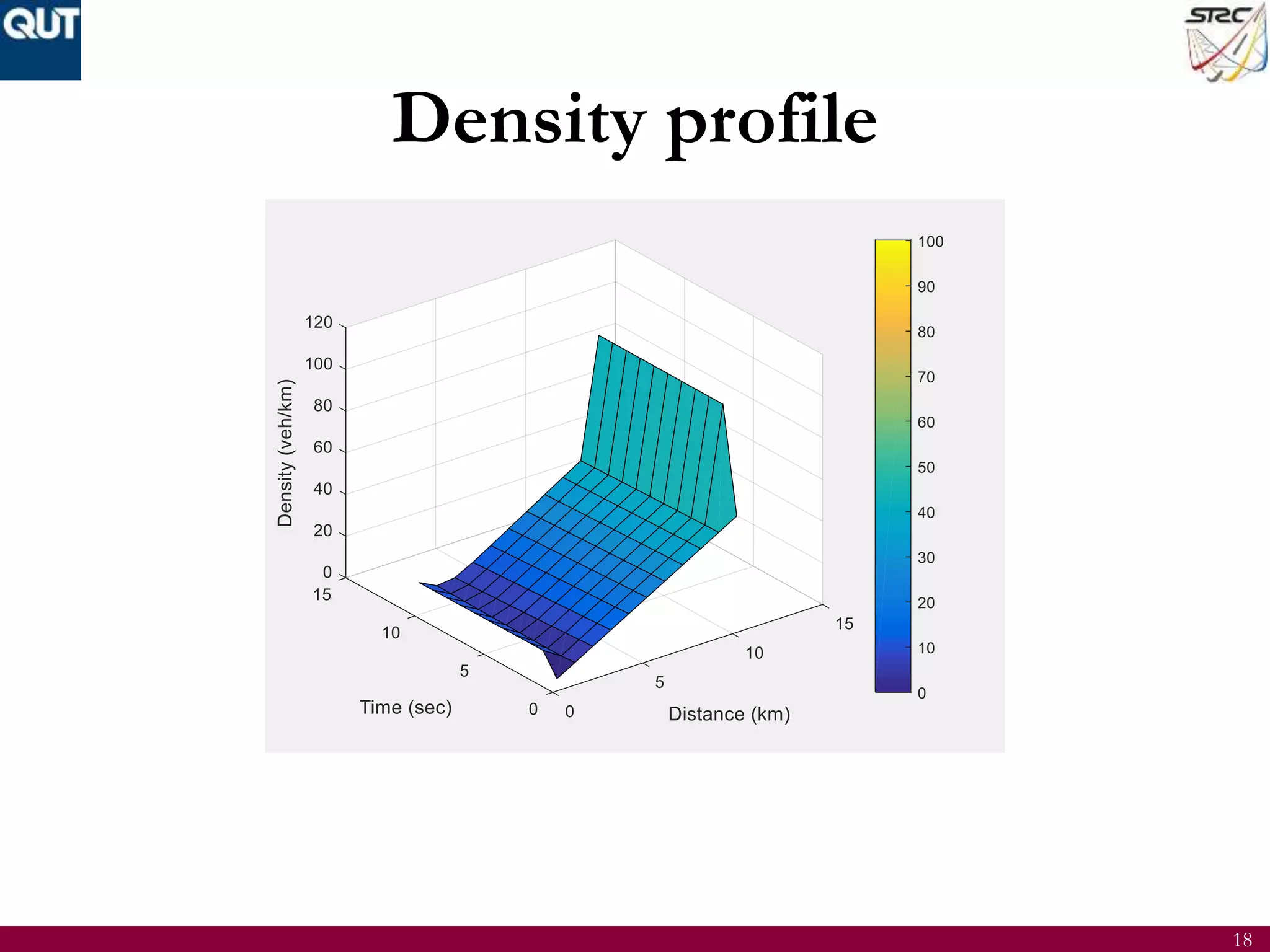
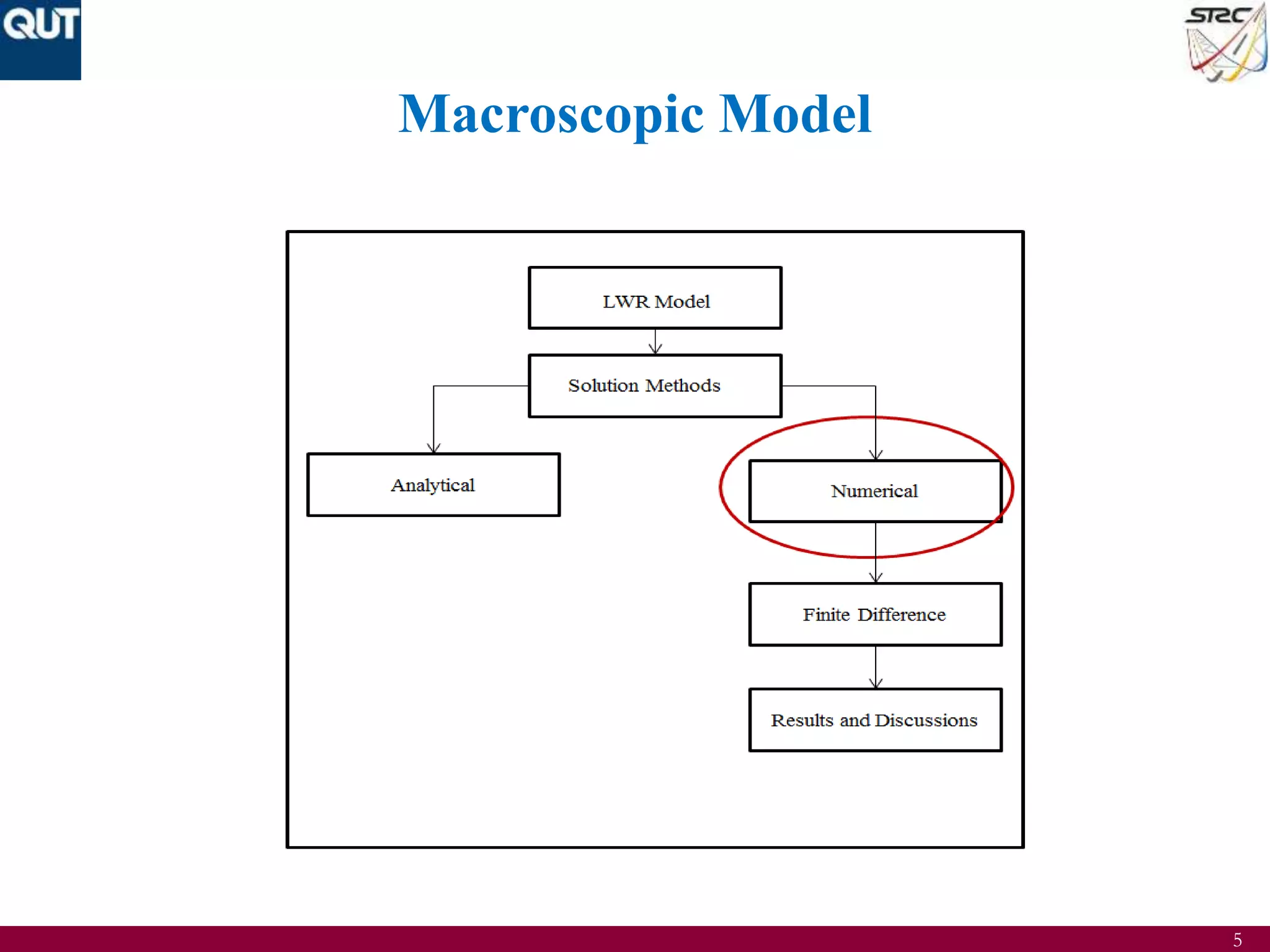
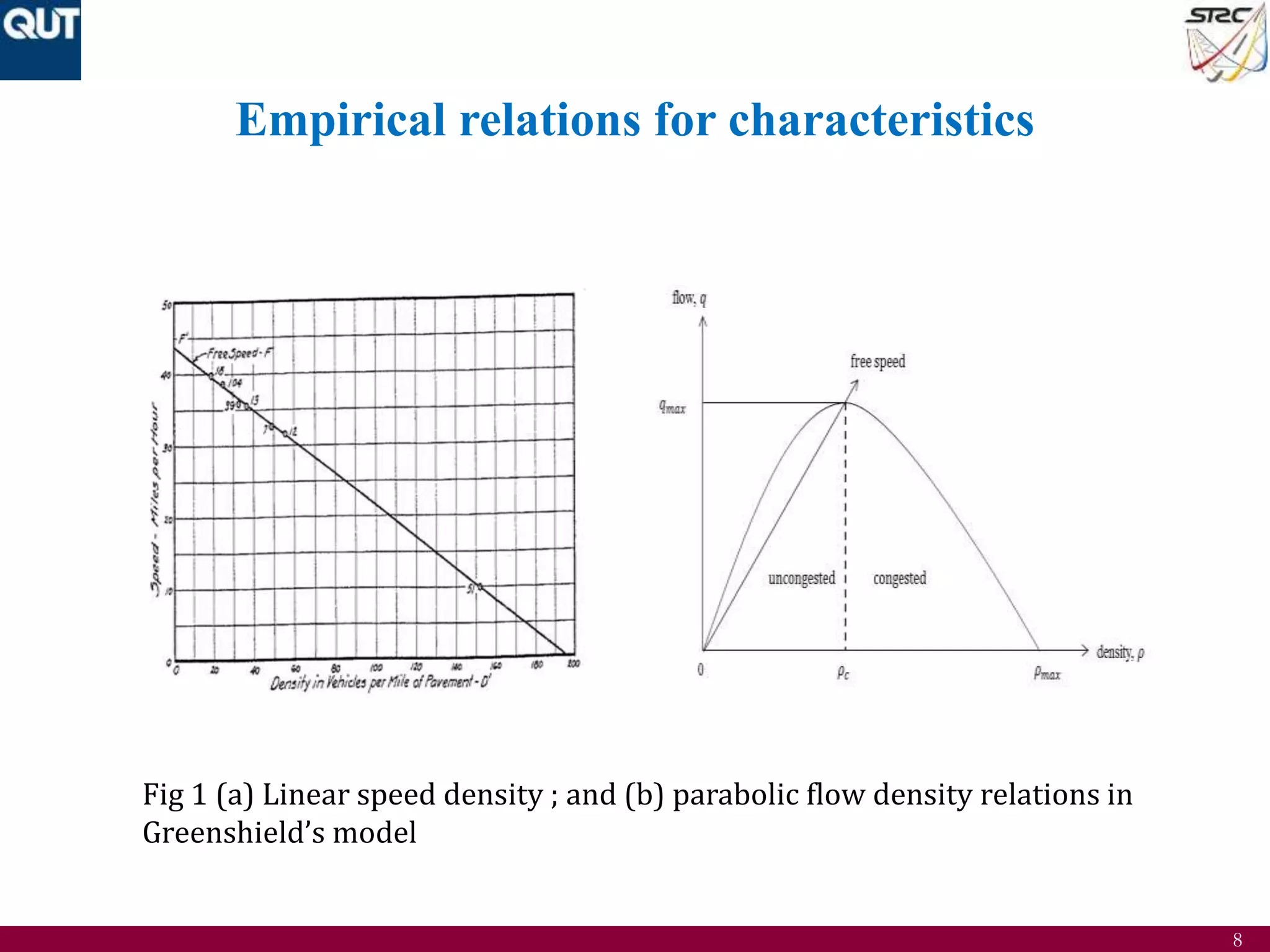
The document discusses the development of mathematical understanding in traffic flow modeling, focusing on both macroscopic and microscopic models. It details various traffic characteristics, fundamental equations, and empirical relations, while also presenting numerical methods such as finite difference for solving the LWR model. Results include traffic density approximations and simulations, demonstrating the model's application in traffic flow analysis.

1. 1
Mathematical Understanding in
Traffic Flow Modelling
by
Sarkar Nikhil Chandra, M.S.
PhD Student

2. 2
Context
Objective:
• Develop mathematical understanding in traffic flow modelling
Application:
• Traffic Simulation

3. 3
Outline
 Traffic models
 Solution methods
 Results and Discussion

4. 4
Traffic Flow Models
o Macroscopic models
o Microscopic models

5. 5
Macroscopic Model

6. 6
Traffic Characteristic
• Flow
• Density
• Speed

7. 7
Fundamental traffic flow equation
Fundamental traffic flow equation:
𝑁𝑜. 𝑜𝑓 𝑉𝑒ℎ𝑖𝑐𝑙𝑒𝑠
𝑈𝑛𝑖𝑡 𝑡𝑖𝑚𝑒
=
𝐷𝑖𝑠𝑡𝑎𝑛𝑐𝑒 𝑡𝑟𝑎𝑣𝑒𝑙𝑙𝑒𝑑 𝑏𝑦 𝑣𝑒ℎ𝑖𝑐𝑙𝑒
𝑈𝑛𝑖𝑡 𝑡𝑖𝑚𝑒
×
𝑁𝑜. 𝑜𝑓 𝑉𝑒ℎ𝑖𝑐𝑙𝑒𝑠
𝑈𝑛𝑖𝑡 𝑑𝑖𝑠𝑡𝑎𝑛𝑐𝑒
𝑓𝑙𝑜𝑤 = 𝑠𝑝𝑒𝑒𝑑 × 𝑑𝑒𝑛𝑠𝑖𝑡𝑦
𝑞 = 𝑣. 𝜌
where, 𝑞 = traffic flow (veh/hr per lane)
𝑣 = flow speed (km/hr)
𝜌 = flow density (vehicles per lane-km)

8. 8
Empirical relations for characteristics
Fig 1 (a) Linear speed density ; and (b) parabolic flow density relations in
Greenshield’s model

9. 9
LWR Model

10. 10
LWR model with Conditions
𝜕𝜌
𝜕𝑡
+
𝜕
𝜕𝑥
𝑣 𝑚𝑎𝑥 𝜌 −
𝜌2
𝜌 𝑚𝑎𝑥
= 0 , 𝑡0 ≤ 𝑡 ≤ 𝑇, 𝑎 ≤ 𝑥 ≤ 𝑏
With I.C. 𝜌 𝑡0, 𝑥 = 𝜌0 𝑥 , 𝑎 ≤ 𝑥 ≤ 𝑏
B.C. 𝜌 𝑡, 𝑎 = 𝜌 𝑎 𝑡 , 𝑡0 ≤ 𝑡 ≤ 𝑇
𝜌 𝑡, 𝑏 = 𝜌 𝑏 𝑡 , 𝑡0 ≤ 𝑡 ≤ 𝑇

11. 11
Finite Difference (FD) Method
Independent variables: space and time
Dependent variable: density
The partial derivatives in LWR model at each grid point are approximated from neighbouring
values by using Taylor’s theorem.
𝜌 𝑥0 + ℎ = 𝜌 𝑥0 + ℎ𝜌 𝑥 𝑥0 +
ℎ2
2!
𝜌 𝑥𝑥 𝑥0 + … +
ℎ 𝑛−1
𝑛 − 1 !
𝜌 𝑛−1 𝑥0 + 𝑂(ℎ 𝑛
)
where 𝜌 𝑥 =
𝜕𝜌
𝜕𝑥
; 𝜌 𝑥𝑥 =
𝜕2 𝜌
𝜕𝑥2; …; 𝜌 𝑛−1 =
𝜕 𝑛−1 𝜌
𝜕𝑥 𝑛−1.
FD approximations:
• Forward difference :
𝜕𝜌
𝜕𝑥
=
𝜌 𝑥0+ℎ −𝜌 𝑥0
ℎ
− 𝑂(ℎ)
• Backward difference:
𝜕𝜌
𝜕𝑥
=
𝜌 𝑥0−ℎ −𝜌 𝑥0
ℎ
+ 𝑂(ℎ)
• Central difference:
𝜕𝜌
𝜕𝑥
=
𝜌 𝑥0+ℎ −𝜌 𝑥0−ℎ
2ℎ
+ 𝑂(ℎ2
)

12. 12
FD Mesh
• Aim to approximate the values of the density function 𝜌(𝑥, 𝑡) on a set of discrete points in 𝑥, 𝑡 plane
• Divide the 𝑥-axis into equally space nodes at distance ∆𝑥
• Divide the 𝑡-axis into equally time nodes at distance ∆𝑡
• 𝑥, 𝑡 plane becomes with mesh points
• Choose any mesh point say 𝑖∆𝑥, 𝑛∆𝑡 ; 𝑖 = 1, 2, … , 𝑀 ; 𝑛 = 0, 1, … , 𝑁 − 1
• We are interested in the value of 𝜌(𝑥, 𝑡) at mesh point 𝑖∆𝑡, 𝑛∆𝑥 denoted as
𝜌𝑖
𝑛
= 𝜌(𝑖∆𝑥, 𝑛∆𝑡)

13. 13
The mesh for FD approximation

14. 14
FD Approximations
𝜕𝜌
𝜕𝑡
≈
𝜌𝑖
𝑛+1
−𝜌𝑖
𝑛
∆𝑡
[Forward difference]
𝜕𝜌
𝜕𝑥
≈
𝜌𝑖+1
𝑛
−𝜌𝑖−1
𝑛
2∆𝑥
[Central difference]

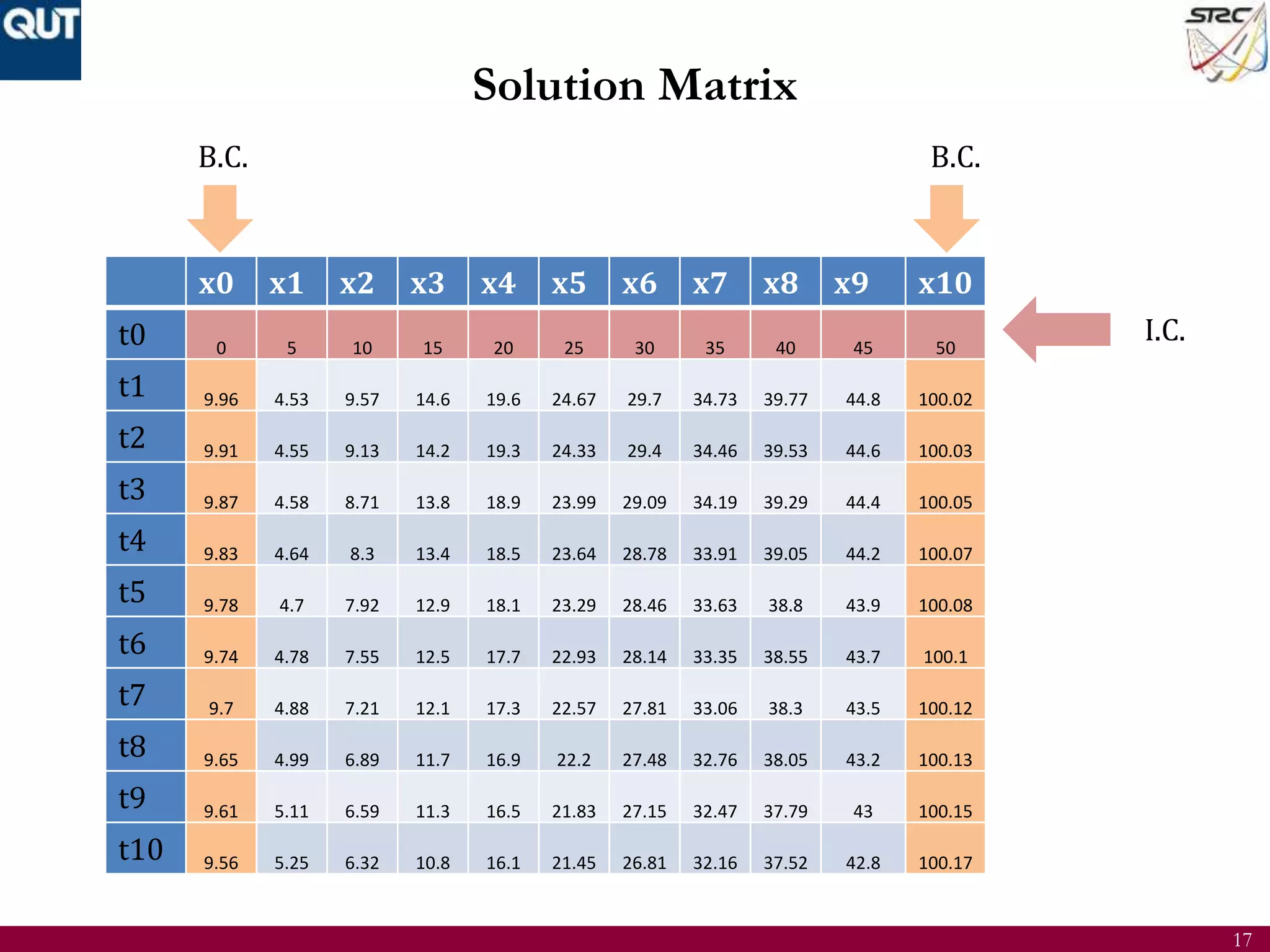
15. 15
Numerical Solution of LWR Model
𝜌𝑖
𝑛+1
= 𝜌𝑖
𝑛
−
∆𝑡
2∆𝑥
[𝑣 𝑚𝑎𝑥(𝜌𝑖+1
𝑛
−
(𝜌𝑖+1
𝑛
)2
𝜌 𝑚𝑎𝑥
) − 𝑣 𝑚𝑎𝑥(𝜌𝑖−1
𝑛
−
(𝜌𝑖−1
𝑛
)2
𝜌 𝑚𝑎𝑥
)]

16. 16
Example of Solution
1. Set ∆𝑡 = 0.1, ∆𝑥 = 0.25 ; 𝑎 = 0; 𝑏 = 2.5; 𝑣 𝑚𝑎𝑥 = 1; 𝜌 𝑚𝑎𝑥 = 150
2. 𝑖𝑛𝑖𝑡𝑖𝑙𝑎 𝑐𝑜𝑛𝑑𝑖𝑡𝑖𝑜𝑛: 𝜌 𝑡0, 𝑥 = 𝜌0 𝑥 = 0.5 𝑥 ; 𝑎 ≤ 𝑥 ≤ 𝑏
3. Boundary conditions:
𝜌 𝑡, 𝑎 =
𝑥 𝑎−𝑣 𝑚𝑎𝑥 𝑡/2
1−𝑣 𝑚𝑎𝑥 𝑡/𝜌 𝑚𝑎𝑥
; 𝑡0 ≤ 𝑡 ≤ 𝑇
𝜌 𝑡, 𝑏 =
𝑥 𝑏−𝑣 𝑚𝑎𝑥 𝑡/2
1−𝑣 𝑚𝑎𝑥 𝑡/𝜌 𝑚𝑎𝑥
; 𝑡0 ≤ 𝑡 ≤ 𝑇
4. Stability condition:
𝑣 𝑚𝑎𝑥∆𝑡
∆𝑥
≤ 1

17. 17
Solution Matrix
x0 x1 x2 x3 x4 x5 x6 x7 x8 x9 x10
t0 0 5 10 15 20 25 30 35 40 45 50
t1 9.96 4.53 9.57 14.6 19.6 24.67 29.7 34.73 39.77 44.8 100.02
t2 9.91 4.55 9.13 14.2 19.3 24.33 29.4 34.46 39.53 44.6 100.03
t3 9.87 4.58 8.71 13.8 18.9 23.99 29.09 34.19 39.29 44.4 100.05
t4 9.83 4.64 8.3 13.4 18.5 23.64 28.78 33.91 39.05 44.2 100.07
t5 9.78 4.7 7.92 12.9 18.1 23.29 28.46 33.63 38.8 43.9 100.08
t6 9.74 4.78 7.55 12.5 17.7 22.93 28.14 33.35 38.55 43.7 100.1
t7 9.7 4.88 7.21 12.1 17.3 22.57 27.81 33.06 38.3 43.5 100.12
t8 9.65 4.99 6.89 11.7 16.9 22.2 27.48 32.76 38.05 43.2 100.13
t9 9.61 5.11 6.59 11.3 16.5 21.83 27.15 32.47 37.79 43 100.15
t10 9.56 5.25 6.32 10.8 16.1 21.45 26.81 32.16 37.52 42.8 100.17
I.C.
B.C.B.C.

18. 18
Density profile

19. 19
Thank you !!!