Downloaded 123 times
Uploaded bymichael mutitu
Mathcad 17-slab design
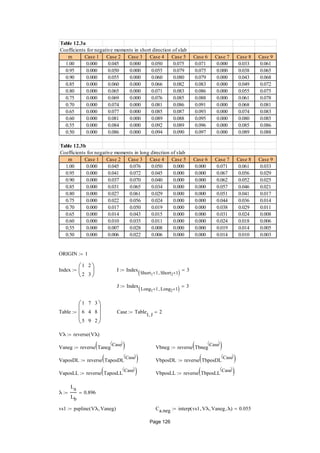
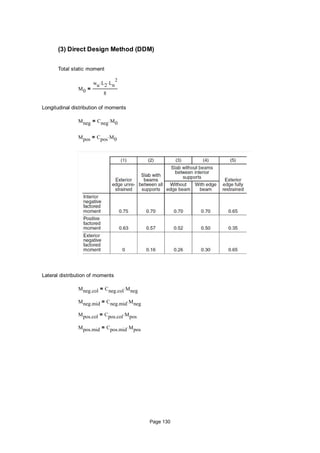
This document discusses the design of one-way and two-way concrete slabs. It provides formulas and steps for determining slab thickness, loads on the slab, bending moments, and steel reinforcement ratios and amounts. An example problem is presented that demonstrates the design of a two-way slab with given dimensions, live load, and material properties. The loads, moments, and reinforcement ratios and areas are calculated for the slab.
More Related Content
Mathcad 17-slab design
- 1. 17. Slab Design A.Design of One-Way Slabs La = length of short side Lb = length of long side La Lb 0.5 : the slab in one-way La Lb 0.5 : the slab is two-way Thickness of one-way slab Simply supported Ln 20 One end continuous Ln 24 Both ends continuous Ln 28 Cantilever Ln 10 Analysis of one-way slab Design scheme: continuous beam Determination of bending moments: using ACI moment coefficients Design of one-way slab Design section: rectangular section of 1m x h Type section: singly reinforced beam Page 115
- 2. Example 17.1 Span ofslab Ln 2m 20cm 1.8m Live load LL 12 kN m 2 Materials f'c 20MPa fy 390MPa Solution Thickness of one-way slab tmin Ln 28 64.286 mm Use t 100mm Loads on slab Cover 50mm 22 kN m 3 1.1 kN m 2 Slab t 25 kN m 3 2.5 kN m 2 Ceiling 0.40 kN m 2 Mechanical 0.20 kN m 2 Partition 1.00 kN m 2 DL Cover Slab Ceiling Mechanical Partition 5.2 kN m 2 wu 1.2 DL 1.6 LL 25.44 kN m 2 Bending moments Msupport 1 11 wu Ln 2 7.493 kN m 1m Mmidspan 1 16 wu Ln 2 5.152 kN m 1m Steel reinforcements Page 116
- 3. β1 0.65 max0.85 0.05 f'c 27.6MPa 6.9MPa min 0.85 0.85 εu 0.003 ρmax 0.85 β1 f'c fy εu εu 0.005 0.014 ρmin max 0.249MPa f'c MPa fy 1.379MPa fy 0.00354 ρshrinkage 0.0020return( ) fy 50ksiif 0.0018return( ) fy 60ksiif max 0.0018 60ksi fy 0.0014 return otherwise ρshrinkage 0.0018 Top rebars b 1m d t 20mm 10mm 2 75 mm Mu Msupport b 7.493 kN m Mn Mu 0.9 8.326 kN m R Mn b d 2 1.48 MPa ρ 0.85 f'c fy 1 1 2 R 0.85 f'c 0.004 ρ ρmax 1 As max ρ b d ρshrinkage b t 2.982 cm 2 As0 π 10mm( ) 2 4 n As As0 smax min 3 t 450mm( ) s min Floor b n 10mm smax 260 mm Bottom rebars Mu Mmidspan b 5.152 kN m Mn Mu 0.9 5.724 kN m Page 117
- 4. R Mn b d 2 1.018 MPa ρ0.85 f'c fy 1 1 2 R 0.85 f'c 0.003 ρ ρmax 1 As max ρ b d ρshrinkage b t 2.019 cm 2 As0 π 10mm( ) 2 4 n As As0 smax min 3 t 450mm( ) s min Floor b n 10mm smax 300 mm Link rebars As ρshrinkage b t 1.8 cm 2 As0 π 10mm( ) 2 4 n As As0 smax min 5 t 450mm( ) s min Floor b n 10mm smax 430 mm B. Design of Two-Way Slabs Design methods: - Load distribution method - Moment coefficient method - Direct design method (DDM) - Equivalent frame method - Strip method - Yield line method Page 118
- 5. (1) Load DistributionMethod Principle: Equality of deflection in short and long directions fa fb= αa wa La 4 EI αb wb Lb 4 EI = Case αa αb= wa wb Lb 4 La 4 = 1 λ 4 = λ La Lb = wa wb wu= From which, wa wu 1 1 λ 4 = wb wu λ 4 1 λ 4 = For λ 1 1 1 λ 4 0.5 λ 4 1 λ 4 0.5 For λ 0.8 1 1 λ 4 0.709 λ 4 1 λ 4 0.291 For λ 0.6 1 1 λ 4 0.885 λ 4 1 λ 4 0.115 For λ 0.5 1 1 λ 4 0.941 λ 4 1 λ 4 0.059 For λ 0.4 1 1 λ 4 0.975 λ 4 1 λ 4 0.025 Page 119
- 6. Example 17.2 Slab dimensionLa 4.3m Lb 5.5m Live load LL 2.00 kN m 2 Materials f'c 20MPa fy 390MPa Solution Thickness of two-way slab Perimeter La Lb 2 tmin Perimeter 180 108.889 mm t 1 30 1 50 La 143.333 86( ) mm Use t 120mm Loads on slab SDL 50mm 22 kN m 3 0.40 kN m 2 1.00 kN m 2 2.5 kN m 2 DL SDL t 25 kN m 3 5.5 kN m 2 LL 2 kN m 2 wu 1.2 DL 1.6 LL 9.8 kN m 2 Load distribution λ La Lb 0.782 wa 1 1 λ 4 wu 7.134 kN m 2 wb λ 4 1 λ 4 wu 2.666 kN m 2 Page 120
- 7. Bending moments Ma.neg 1 11 wa La 2 11.992 kN m 1m Ma.pos 1 16 wa La 2 8.245 kN m 1m Mb.neg 1 11 wb Lb 2 7.33 kN m 1m Mb.pos 1 16 wb Lb 2 5.04 kN m 1m Steel reinforcements β1 0.65 max 0.85 0.05 f'c 27.6MPa 6.9MPa min 0.85 0.85 εu 0.003 ρmax 0.85 β1 f'c fy εu εu 0.005 0.014 ρmin max 0.249MPa f'c MPa fy 1.379MPa fy 0.00354 ρshrinkage 0.0020return( ) fy 50ksiif 0.0018return( ) fy 60ksiif max 0.0018 60ksi fy 0.0014 return otherwise ρshrinkage 0.0018 Top rebar in short direction b 1m d t 20mm 10mm 10mm 2 85 mm Mu Ma.neg b 11.992 kN m Mn Mu 0.9 13.325 kN m R Mn b d 2 1.844 MPa Page 121
- 8. ρ 0.85 f'c fy 11 2 R 0.85 f'c 0.005 ρ ρmax 1 As max ρ b d ρshrinkage b t 4.265 cm 2 As0 π 10mm( ) 2 4 n As As0 smax min 2 t 450mm( ) s min Floor b n 10mm smax 180 mm Bottom rebar in short direction Mu Ma.pos b 8.245 kN m Mn Mu 0.9 9.161 kN m R Mn b d 2 1.268 MPa ρ 0.85 f'c fy 1 1 2 R 0.85 f'c 0.003 ρ ρmax 1 As max ρ b d ρshrinkage b t 2.875 cm 2 As0 π 10mm( ) 2 4 n As As0 smax min 2 t 450mm( ) s min Floor b n 10mm smax 240 mm Top rebar in long direction Mu Mb.neg b 7.33 kN m Mn Mu 0.9 8.145 kN m R Mn b d 2 1.127 MPa ρ 0.85 f'c fy 1 1 2 R 0.85 f'c 0.003 ρ ρmax 1 As max ρ b d ρshrinkage b t 2.544 cm 2 Page 122
- 9. As0 π 10mm( ) 2 4 n As As0 smax min 2 t 450mm( ) s min Floor b n 10mm smax 240 mm Bottom rebar in long direction Mu Mb.pos b 5.04 kN m Mn Mu 0.9 5.599 kN m R Mn b d 2 0.775 MPa ρ 0.85 f'c fy 1 1 2 R 0.85 f'c 0.002 ρ ρmax 1 As max ρ b d ρshrinkage b t 2.16 cm 2 As0 π 10mm( ) 2 4 n As As0 smax min 2 t 450mm( ) s min Floor b n 10mm smax 240 mm Shrinkage rebars b 1m As ρshrinkage b t 2.16 cm 2 As0 π 10mm( ) 2 4 n As As0 smax min 5 t 450mm( ) s min Floor b n 10mm smax 360 mm Page 123
- 10. (2) Moment CoefficientMethod Negative moments Ma.neg Ca.neg wu La 2 = Mb.neg Cb.neg wu Lb 2 = Positive moments Ma.pos Ca.pos.DL wD La 2 Ca.pos.LL wL La 2 = Mb.pos Cb.pos.DL wD Lb 2 Cb.pos.LL wL Lb 2 = where Ca.neg Cb.neg Ca.pos.DL Ca.pos.LL Cb.pos.DL Cb.pos.LL are tabulated moment coefficients wD 1.2 DL= wL 1.6 LL= wu 1.2 1.6 LL= Example 17.3 Slab dimension La 5.0m 25cm 4.75 m Lb 5.5m 20cm 5.3m Live load for office LL 2.40 kN m 2 Materials f'c 20MPa fy 390MPa Boundary conditions in short and long directions Simple Continuous 0 1 Short Continuous Continuous Long Continuous Continuous Solution Thickness of two-way slab Perimeter La Lb 2 Page 124
- 11. tmin Perimeter 180 111.667 mm t 1 30 1 50 La 158.33395( ) mm Use t 120mm Loads on slab Cover 50mm 22 kN m 3 1.1 kN m 2 Slab t 25 kN m 3 3 kN m 2 Ceiling 0.40 kN m 2 Partition 1.00 kN m 2 SDL Cover Ceiling Partition 2.5 kN m 2 DL SDL Slab 5.5 kN m 2 wD 1.2 DL LL 2.4 kN m 2 wL 1.6 LL wu 1.2 DL 1.6LL 10.44 kN m 2 Moment coefficients Page 125
- 12. Table 12.3a Coefficients fornegative moments in short direction of slab m Case 1 Case 2 Case 3 Case 4 Case 5 Case 6 Case 7 Case 8 Case 9 1.00 0.000 0.045 0.000 0.050 0.075 0.071 0.000 0.033 0.061 0.95 0.000 0.050 0.000 0.055 0.079 0.075 0.000 0.038 0.065 0.90 0.000 0.055 0.000 0.060 0.080 0.079 0.000 0.043 0.068 0.85 0.000 0.060 0.000 0.066 0.082 0.083 0.000 0.049 0.072 0.80 0.000 0.065 0.000 0.071 0.083 0.086 0.000 0.055 0.075 0.75 0.000 0.069 0.000 0.076 0.085 0.088 0.000 0.061 0.078 0.70 0.000 0.074 0.000 0.081 0.086 0.091 0.000 0.068 0.081 0.65 0.000 0.077 0.000 0.085 0.087 0.093 0.000 0.074 0.083 0.60 0.000 0.081 0.000 0.089 0.088 0.095 0.000 0.080 0.085 0.55 0.000 0.084 0.000 0.092 0.089 0.096 0.000 0.085 0.086 0.50 0.000 0.086 0.000 0.094 0.090 0.097 0.000 0.089 0.088 Table 12.3b Coefficients for negative moments in long direction of slab m Case 1 Case 2 Case 3 Case 4 Case 5 Case 6 Case 7 Case 8 Case 9 1.00 0.000 0.045 0.076 0.050 0.000 0.000 0.071 0.061 0.033 0.95 0.000 0.041 0.072 0.045 0.000 0.000 0.067 0.056 0.029 0.90 0.000 0.037 0.070 0.040 0.000 0.000 0.062 0.052 0.025 0.85 0.000 0.031 0.065 0.034 0.000 0.000 0.057 0.046 0.021 0.80 0.000 0.027 0.061 0.029 0.000 0.000 0.051 0.041 0.017 0.75 0.000 0.022 0.056 0.024 0.000 0.000 0.044 0.036 0.014 0.70 0.000 0.017 0.050 0.019 0.000 0.000 0.038 0.029 0.011 0.65 0.000 0.014 0.043 0.015 0.000 0.000 0.031 0.024 0.008 0.60 0.000 0.010 0.035 0.011 0.000 0.000 0.024 0.018 0.006 0.55 0.000 0.007 0.028 0.008 0.000 0.000 0.019 0.014 0.005 0.50 0.000 0.006 0.022 0.006 0.000 0.000 0.014 0.010 0.003 ORIGIN 1 Index 1 2 2 3 I Index Short1 1 Short2 1 3 J Index Long1 1 Long2 1 3 Table 1 6 5 7 4 9 3 8 2 Case Table I J 2 Vλ reverse Vλ( ) Vaneg reverse Taneg Case Vbneg reverse Tbneg Case VaposDL reverse TaposDL Case VbposDL reverse TbposDL Case VaposLL reverse TaposLL Case VbposLL reverse TbposLL Case λ La Lb 0.896 vs1 pspline Vλ Vaneg( ) Ca.neg interp vs1 Vλ Vaneg λ( ) 0.055 Page 126
- 13. vs2 pspline VλVbneg( ) Cb.neg interp vs2 Vλ Vbneg λ( ) 0.037 vs3 pspline Vλ VaposDL( ) Ca.pos.DL interp vs3 Vλ VaposDL λ( ) 0.022 vs4 pspline Vλ VbposDL( ) Cb.pos.DL interp vs4 Vλ VbposDL λ( ) 0.014 vs5 pspline Vλ VaposLL( ) Ca.pos.LL interp vs5 Vλ VaposLL λ( ) 0.034 vs6 pspline Vλ VbposLL( ) Cb.pos.LL interp vs6 Vλ VbposLL λ( ) 0.022 Bending moments Ma.neg Ca.neg wu La 2 13.043 kN m 1m Mb.neg Cb.neg wu Lb 2 10.729 kN m 1m Ma.pos Ca.pos.DL wD La 2 Ca.pos.LL wL La 2 6.266 kN m 1m Mb.pos Cb.pos.DL wD Lb 2 Cb.pos.LL wL Lb 2 4.911 kN m 1m Steel reinforcements β1 0.65 max 0.85 0.05 f'c 27.6MPa 6.9MPa min 0.85 0.85 εu 0.003 ρmax 0.85 β1 f'c fy εu εu 0.005 0.014 ρmin max 0.249MPa f'c MPa fy 1.379MPa fy 0.00354 ρshrinkage 0.0020return( ) fy 50ksiif 0.0018return( ) fy 60ksiif max 0.0018 60ksi fy 0.0014 return otherwise ρshrinkage 0.0018 Top rebars in short direction b 1m d t 20mm 10mm 10mm 2 85 mm Page 127
- 14. Mu Ma.neg b13.043 kN m Mn Mu 0.9 14.492 kN m R Mn b d 2 2.006 MPa ρ 0.85 f'c fy 1 1 2 R 0.85 f'c 0.005 ρ ρmax 1 As max ρ b d ρshrinkage b t 4.666 cm 2 As0 π 10mm( ) 2 4 n As As0 smax min 2 t 450mm( ) s min Floor b n 10mm smax 160 mm Bottom rebars in short direction Mu Ma.pos b 6.266 kN m Mn Mu 0.9 6.963 kN m R Mn b d 2 0.964 MPa ρ 0.85 f'c fy 1 1 2 R 0.85 f'c 0.003 ρ ρmax 1 As max ρ b d ρshrinkage b t 2.163 cm 2 As0 π 10mm( ) 2 4 n As As0 smax min 2 t 450mm( ) s min Floor b n 10mm smax 240 mm Top rebars in long direction Mu Mb.neg b 10.729 kN m Mn Mu 0.9 11.921 kN m Page 128
- 15. R Mn b d 2 1.65 MPa ρ0.85 f'c fy 1 1 2 R 0.85 f'c 0.004 ρ ρmax 1 As max ρ b d ρshrinkage b t 3.79 cm 2 As0 π 10mm( ) 2 4 n As As0 smax min 2 t 450mm( ) s min Floor b n 10mm smax 200 mm Bottom rebars in long direction Mu Mb.pos b 4.911 kN m Mn Mu 0.9 5.457 kN m R Mn b d 2 0.755 MPa ρ 0.85 f'c fy 1 1 2 R 0.85 f'c 0.002 ρ ρmax 1 As max ρ b d ρshrinkage b t 2.16 cm 2 As0 π 10mm( ) 2 4 n As As0 smax min 2 t 450mm( ) s min Floor b n 10mm smax 240 mm Shrinkage rebars b 1m As ρshrinkage b t 2.16 cm 2 As0 π 10mm( ) 2 4 n As As0 smax min 5 t 450mm( ) s min Floor b n 10mm smax 360 mm Page 129
- 16. (3) Direct DesignMethod (DDM) Total static moment M0 wu L2 Ln 2 8 = Longitudinal distribution of moments Mneg Cneg M0= Mpos Cpos M0= Lateral distribution of moments Mneg.col Cneg.col Mneg= Mneg.mid Cneg.mid Mneg= Mpos.col Cpos.col Mpos= Mpos.mid Cpos.mid Mpos= Page 130
- 17. Example 17.4 Slab dimensionLa 4m Lb 6m Live load for hospital LL 3.00 kN m 2 Materials f'c 25MPa fy 390MPa Page 131
- 18. Solution Section of beamin long direction L Lb 6 m h 1 10 1 15 L 600 400( ) mm h 500mm b 0.3 0.6( ) h 150 300( ) mm b 250mm bb hb b h Section of beam in short direction L La 4 m h 1 10 1 15 L 400 266.667( ) mm h 300mm b 0.3 0.6( ) h 90 180( ) mm b 200mm ba ha b h Determination of slab thickness Perimeter La Lb 2 tmin Perimeter 180 111.111 mm Assume t 120mm In long direction bw bb h hb hf t hw h hf b min bw 2 hw bw 8 hf 1.01 m A1 bw h x1 h 2 A2 b bw hf x2 hf 2 xc x1 A1 x2 A2 A1 A2 169.852 mm I1 bw h 3 12 A1 x1 xc 2 I2 b bw hf 3 12 A2 x2 xc 2 Page 132
- 19. Ib I1 I24.617 10 5 cm 4 Is La hf 3 12 wc 24 kN m 3 Ec 44MPa wc kN m 3 1.5 f'c MPa 2.587 10 4 MPa α Ec Ib Ec Is 8.016 αb α In short direction bw ba h ha hf t hw h hf b min bw 2 hw bw 8 hf 0.56 m A1 bw h x1 h 2 A2 b bw hf x2 hf 2 xc x1 A1 x2 A2 A1 A2 112.326 mm I1 bw h 3 12 A1 x1 xc 2 I2 b bw hf 3 12 A2 x2 xc 2 Ib I1 I2 7.053 10 4 cm 4 Iba Ib Is Lb hf 3 12 8.64 10 4 cm 4 α Ec Ib Ec Is 0.816 αa α Required thickness of slab αm αa 2 αb 2 4 4.416 β Lb La 1.5 Ln Lb 20cm 5.8m Page 133
- 20. hf max Ln 0.8 fy 200ksi 365 β αm 0.2 5in 0.2 αm 2.0if max Ln 0.8 fy 200ksi 36 9 β 3.5in 2.0 αm 5.0if "DDM is not applied" otherwise hf 126.876 mm Loads on slab DL 50mm 22 kN m 3 t 25 kN m 3 0.40 kN m 2 1.00 kN m 2 5.5 kN m 2 LL 3 kN m 2 wu 1.2 DL 1.6 LL 11.4 kN m 2 In long direction L1 Lb 6 m Ln L1 ba 5.8m L2 La 4 m α1 αb 8.016 Total static moment M0 wu L2 Ln 2 8 191.748 kN m Longitudinal distribution of moments Mneg 0.65 M0 124.636 kN m Mpos 0.35 M0 67.112 kN m Lateral distribution of moments k1 L2 L1 0.667 k2 α1 L2 L1 5.344 linterp2 VX VY M x y( ) V j linterp VX M j x j 1 rows VY( )for linterp VY V y( ) Page 134
- 21. Cneg.col linterp2 0 1 10 0.5 1.0 2.0 0.75 0.90 0.90 0.75 0.75 0.75 0.75 0.45 0.45 k2k1 0.85 Cneg.mid 1 Cneg.col 0.15 Cpos.col linterp2 0 1 10 0.5 1.0 2.0 0.60 0.90 0.90 0.60 0.75 0.75 0.60 0.45 0.45 k2 k1 0.85 Cpos.mid 1 Cpos.col 0.15 Mneg.col Cneg.col Mneg 105.941 kN m Mneg.mid Cneg.mid Mneg 18.695 kN m Mpos.col Cpos.col Mpos 57.045 kN m Mpos.mid Cpos.mid Mpos 10.067 kN m Ccol.beam linterp 0 1 10 0 0.85 0.85 k2 0.85 Ccol.slab 1 Ccol.beam 0.15 Mneg.col.beam Ccol.beam Mneg.col 90.05 kN m Mneg.col.slab Ccol.slab Mneg.col 15.891 kN m Mpos.col.beam Ccol.beam Mpos.col 48.488 kN m Mpos.col.slab Ccol.slab Mpos.col 8.557 kN m bcol min L1 L2 4 2 2 m bmid L2 bcol 2 m Top rebars in column strip b bcol d t 20mm 10mm 10mm 2 85 mm Mu Mneg.col.slab 15.891 kN m Mn Mu 0.9 17.657 kN m Page 135
- 22. R Mn b d 2 1.222 MPa ρ0.85 f'c fy 1 1 2 R 0.85 f'c 0.003 ρ ρmax 1 As max ρ b d ρshrinkage b t 5.489 cm 2 As0 π 10mm( ) 2 4 n As As0 smax min 2 t 450mm( ) s min Floor b n 10mm smax 240 mm Bottom rebars in column strip Mu Mpos.col.slab 8.557 kN m Mn Mu 0.9 9.508 kN m R Mn b d 2 0.658 MPa ρ 0.85 f'c fy 1 1 2 R 0.85 f'c 0.002 ρ ρmax 1 As max ρ b d ρshrinkage b t 4.32 cm 2 As0 π 10mm( ) 2 4 n As As0 smax min 2 t 450mm( ) s min Floor b n 10mm smax 240 mm Top rebars in middle strip b bmid Mu Mneg.mid 18.695 kN m Mn Mu 0.9 20.773 kN m R Mn b d 2 1.438 MPa ρ 0.85 f'c fy 1 1 2 R 0.85 f'c 0.004 ρ ρmax 1 Page 136
- 23. As max ρb d ρshrinkage b t 6.494 cm 2 As0 π 10mm( ) 2 4 n As As0 smax min 2 t 450mm( ) s min Floor b n 10mm smax 240 mm Bottom rebars in middle strip Mu Mpos.mid 10.067 kN m Mn Mu 0.9 11.185 kN m R Mn b d 2 0.774 MPa ρ 0.85 f'c fy 1 1 2 R 0.85 f'c 0.002 ρ ρmax 1 As max ρ b d ρshrinkage b t 4.32 cm 2 As0 π 10mm( ) 2 4 n As As0 smax min 2 t 450mm( ) s min Floor b n 10mm smax 240 mm In short direction L1 La 4 m Ln L1 bb 3.75 m L2 Lb 6 m α1 αa 0.816 Total static moment M0 wu L2 Ln 2 8 120.234 kN m Longitudinal distribution of moments Mneg 0.65 M0 78.152 kN m Mpos 0.35 M0 42.082 kN m Lateral distribution of moments Page 137
- 24. k1 L2 L1 1.5 k2 α1 L2 L1 1.224 Cneg.col linterp2 0 1 10 0.5 1.0 2.0 0.75 0.90 0.90 0.75 0.75 0.75 0.75 0.45 0.45 k2 k1 0.6 Cneg.mid 1 Cneg.col 0.4 Cpos.col linterp2 0 1 10 0.5 1.0 2.0 0.60 0.90 0.90 0.60 0.75 0.75 0.60 0.45 0.45 k2 k1 0.6 Cpos.mid 1 Cpos.col 0.4 Mneg.col Cneg.col Mneg 46.891 kN m Mneg.mid Cneg.mid Mneg 31.261 kN m Mpos.col Cpos.col Mpos 25.249 kN m Mpos.mid Cpos.mid Mpos 16.833 kN m Ccol.beam linterp 0 1 10 0 0.85 0.85 k2 0.85 Ccol.slab 1 Ccol.beam 0.15 Mneg.col.beam Ccol.beam Mneg.col 39.858 kN m Mneg.col.slab Ccol.slab Mneg.col 7.034 kN m Mpos.col.beam Ccol.beam Mpos.col 21.462 kN m Mpos.col.slab Ccol.slab Mpos.col 3.787 kN m bcol min L1 L2 4 2 2 m bmid L2 bcol 4 m Top rebars in column strip b bcol Mu Mneg.col.slab 7.034 kN m Mn Mu 0.9 7.815 kN m Page 138
- 25. R Mn b d 2 0.541 MPa ρ0.85 f'c fy 1 1 2 R 0.85 f'c 0.001 ρ ρmax 1 As max ρ b d ρshrinkage b t 4.32 cm 2 As0 π 10mm( ) 2 4 n As As0 smax min 2 t 450mm( ) s min Floor b n 10mm smax 240 mm Bottom rebars in column strip Mu Mpos.col.slab 3.787 kN m Mn Mu 0.9 4.208 kN m R Mn b d 2 0.291 MPa ρ 0.85 f'c fy 1 1 2 R 0.85 f'c 0.001 ρ ρmax 1 As max ρ b d ρshrinkage b t 4.32 cm 2 As0 π 10mm( ) 2 4 n As As0 smax min 2 t 450mm( ) s min Floor b n 10mm smax 240 mm Top rebars in middle strip b bmid Mu Mneg.mid 31.261 kN m Mn Mu 0.9 34.734 kN m R Mn b d 2 1.202 MPa ρ 0.85 f'c fy 1 1 2 R 0.85 f'c 0.003 ρ ρmax 1 Page 139
- 26. As max ρb d ρshrinkage b t 10.792 cm 2 As0 π 10mm( ) 2 4 n As As0 smax min 2 t 450mm( ) s min Floor b n 10mm smax 240 mm Bottom rebars in middle strip Mu Mpos.mid 16.833 kN m Mn Mu 0.9 18.703 kN m R Mn b d 2 0.647 MPa ρ 0.85 f'c fy 1 1 2 R 0.85 f'c 0.002 ρ ρmax 1 As max ρ b d ρshrinkage b t 8.64 cm 2 As0 π 10mm( ) 2 4 n As As0 smax min 2 t 450mm( ) s min Floor b n 10mm smax 240 mm Page 140
- 27.