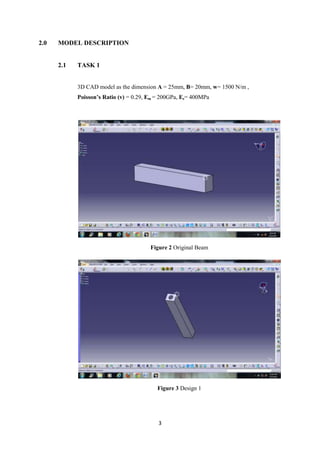
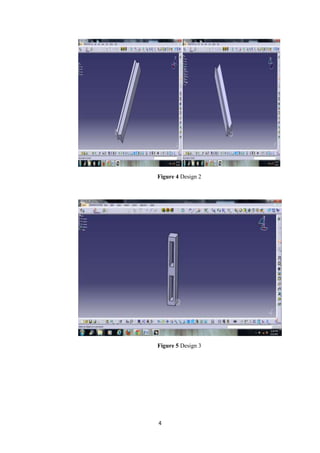
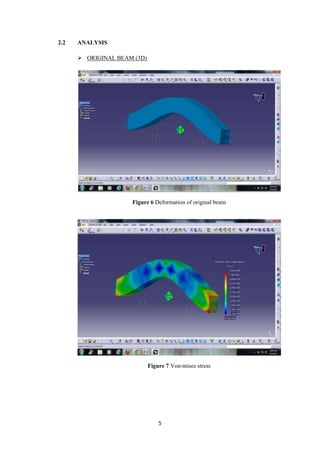
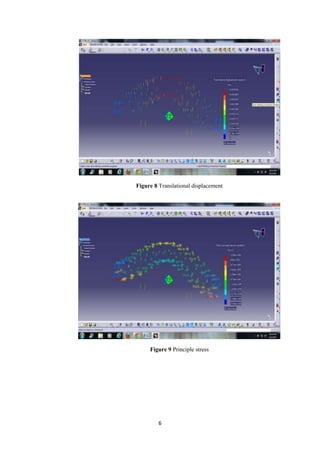
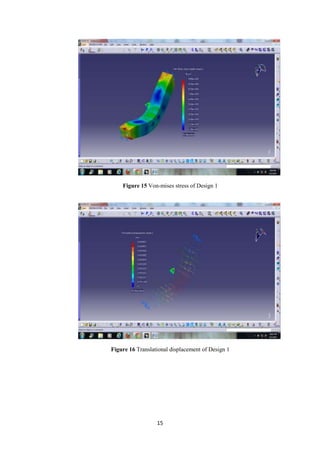
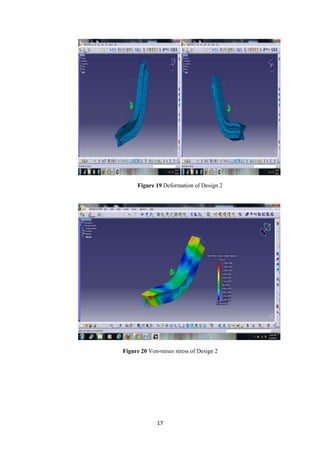
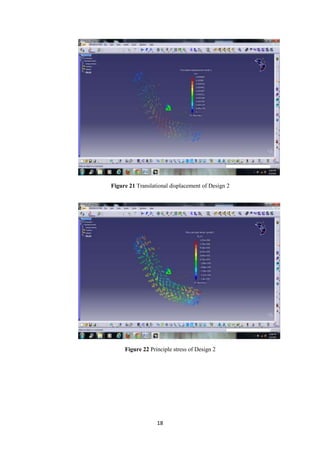
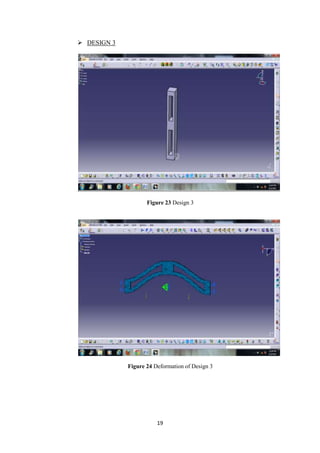
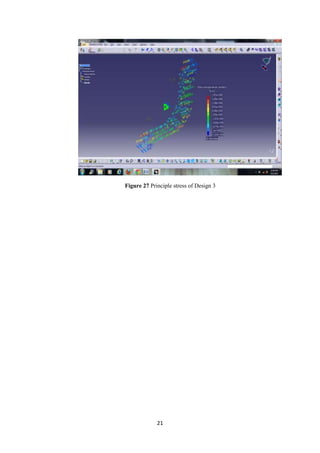
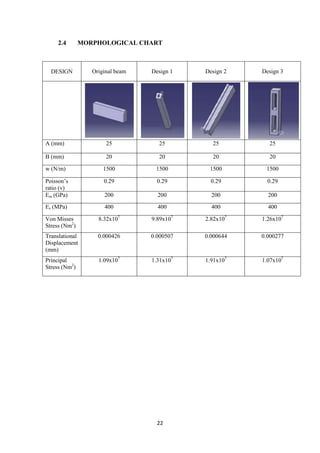
The document describes the engineering design process and finite element analysis (FEA). It summarizes that the engineering design process is iterative and involves research, conceptualization, design, and production. It then explains that FEA uses the finite element method to approximate solutions to partial differential equations by dividing a complex problem into smaller, solvable elements. FEA is well-suited for problems over complicated domains, changing domains, solutions with varying precision, or non-smooth solutions like crash simulations.

1. 1.0 INTRODUCTION
The Engineering Design Process outlines the steps necessary in solving any type of
engineering problems. The engineering design process is a multi-step process including the
research, conceptualization, feasibility assessment, establishing design requirements,
preliminary design, detailed design, production planning and tool design, and finally
production. The sections to follow are not necessarily steps in the engineering design process,
for some tasks are completed at the same time as other tasks. This is just a general summary
of each part of the engineering design process. The Engineering Design Process is not a linear
process. Successful engineering requires going back and forth between the six main steps as
shown in Figure 1.
Figure 1 Engineering design process
During the engineering design process, designers frequently jump back and forth between
steps. Going back to earlier steps is common. This way of working is called iteration, and it is
likely that our process will do the same.
1

2. In this project, we have to use the finite element method (FEM). Its practical application
often known as finite element analysis (FEA)) which is a numerical technique for finding
approximate solutions to partial differential equations (PDE) and their systems, as well as
(less often) integral equations. In simple terms, FEM is a method for dividing up a very
complicated problem into small elements that can be solved in relation to each other. FEM is
a special case of the more general Galerkin method with polynomial approximation
functions. The solution approach is based on eliminating the spatial derivatives from the
PDE. This approximates the PDE with
 a system of algebraic equations for steady state problems,
 a system of ordinary differential equations for transient problems.
These equation systems are linear if the underlying PDE is linear, and vice versa.
Algebraic equation systems are solved using numerical linear algebra methods. Ordinary
differential equations that arise in transient problems are then numerically integrated using
standard techniques such asEuler's method or the Runge-Kutta method.
In solving partial differential equations, the primary challenge is to create an equation
that approximates the equation to be studied, but is numerically stable, meaning that errors in
the input and intermediate calculations do not accumulate and cause the resulting output to be
meaningless. There are many ways of doing this, all with advantages and disadvantages. The
finite element method is a good choice for solving partial differential equations over
complicated domains (like cars and oil pipelines), when the domain changes (as during a
solid state reaction with a moving boundary), when the desired precision varies over the
entire domain, or when the solution lacks smoothness. For instance, in a frontal crash
simulation it is possible to increase prediction accuracy in "important" areas like the front of
the car and reduce it in its rear (thus reducing cost of the simulation). Another example would
be in Numerical weather prediction, where it is more important to have accurate predictions
over developing highly nonlinear phenomena (such as tropical cyclones in the atmosphere,
or eddies in the ocean) rather than relatively calm areas.
2

3. 2.0 MODEL DESCRIPTION
2.1 TASK 1
3D CAD model as the dimension A = 25mm, B= 20mm, w= 1500 N/m ,
Poisson’s Ratio (v) = 0.29, Em = 200GPa, Es= 400MPa
Figure 2 Original Beam
Figure 3 Design 1
3

4. Figure 4 Design 2
Figure 5 Design 3
4

5. 2.2 ANALYSIS
 ORIGINAL BEAM (3D)
Figure 6 Deformation of original beam
Figure 7 Von-mises stress
5

6. Figure 8 Translational displacement
Figure 9 Principle stress
6

7. Figure 10 Max & min nodal of Von-mises
Figure 11 Max & min nodal of translational displacement
7

8. Figure 12 Max & min nodal of principle stress
Original Beam
MESH:
Entity Size
Nodes 256
Elements 771
ELEMENT TYPE:
Connectivity Statistics
TE4 771 ( 100.00% )
8

9. ELEMENT QUALITY:
Criterion Good Poor Bad Worst Average
771 (
Stretch 0 ( 0.00% ) 0 ( 0.00% ) 0.410 0.587
100.00% )
771 (
Aspect Ratio 0 ( 0.00% ) 0 ( 0.00% ) 3.865 2.234
100.00% )
Materials.1
Material Steel
Young's modulus 2e+011N_m2
Poisson's ratio 0.29
Density 7860kg_m3
Coefficient of thermal expansion 1.17e-005_Kdeg
Yield strength 4e+008N_m2
Static Case
Boundary Conditions
Figure 1
STRUCTURE Computation
Number of nodes : 256
Number of elements : 771
Number of D.O.F. : 768
Number of Contact relations : 0
Number of Kinematic relations : 0
Linear tetrahedron : 771
9

10. RESTRAINT Computation
Name: Restraints.1
Number of S.P.C : 90
LOAD Computation
Name: Loads.1
Applied load resultant :
STIFFNESS Computation
Number of lines : 768
Number of coefficients : 12642
Number of blocks : 1
Maximum number of coefficients per bloc : 12642
Total matrix size : 0 . 15 Mb
SINGULARITY Computation
Restraint: Restraints.1
Number of local singularities : 0
Number of singularities in translation : 0
Number of singularities in rotation : 0
Generated constraint type : MPC
CONSTRAINT Computation
Restraint: Restraints.1
Number of constraints : 90
Number of coefficients : 0
Number of factorized constraints : 90
Number of coefficients : 0
Number of deferred constraints : 0
FACTORIZED Computation
Method : SPARSE
Number of factorized degrees : 678
Number of supernodes : 135
Number of overhead indices : 3954
Number of coefficients : 26211
Maximum front width : 72
Maximum front size : 2628
10

11. Size of the factorized matrix (Mb) : 0 . 199974
Number of blocks : 1
Number of Mflops for factorization : 1 . 356e+000
Number of Mflops for solve : 1 . 082e-001
Minimum relative pivot : 2 . 764e-002
Minimum and maximum pivot
Value Dof Node x (mm) y (mm) z (mm)
2.8078e+008 Tx 256 5.5259e+000 6.5176e+000 2.6446e+001
1.2646e+010 Ty 221 1.4819e+001 5.8076e+000 1.1835e+002
Minimum pivot
Value Dof Node x (mm) y (mm) z (mm)
3.1157e+008 Ty 256 5.5259e+000 6.5176e+000 2.6446e+001
8.5879e+008 Ty 240 8.8304e+000 1.2999e+001 1.0319e+002
8.8355e+008 Tz 225 1.0611e+001 1.9616e+001 5.6535e+001
8.8865e+008 Tx 244 6.1865e+000 5.9668e+000 8.2072e+001
8.9038e+008 Tz 243 1.0395e+001 1.3270e+001 9.3997e+001
8.9809e+008 Tz 226 1.0087e+001 1.9574e+001 6.5662e+001
9.0152e+008 Ty 251 1.0388e+001 1.3258e+001 5.6463e+001
9.0499e+008 Tx 227 9.4759e+000 1.9519e+001 7.4732e+001
9.1072e+008 Tx 226 1.0087e+001 1.9574e+001 6.5662e+001
Translational pivot distribution
Value Percentage
10.E8 --> 10.E9 3.0973e+000
10.E9 --> 10.E10 9.6313e+001
10.E10 --> 10.E11 5.8997e-001
DIRECT METHOD Computation
Name: Static Case Solution.1
Restraint: Restraints.1
Load: Loads.1
Strain Energy : 2.495e-005 J
11

12. Equilibrium
Applied Relative
Components Reactions Residual
Forces Magnitude Error
Fx (N) -2.2500e+002 2.2500e+002 9.9476e-013 2.3287e-014
Fy (N) -2.4980e-014 8.9084e-013 8.6586e-013 2.0270e-014
Fz (N) 4.5157e-014 7.1487e-013 7.6003e-013 1.7792e-014
Mx (Nxm) -1.0037e-014 -7.6279e-014 -8.6316e-014 1.3471e-014
My (Nxm) -1.6875e+001 1.6875e+001 1.5277e-013 2.3842e-014
Mz (Nxm) 2.8125e+000 -2.8125e+000 5.0626e-014 7.9011e-015
Static Case Solution.1 - Deformed mesh.2
Figure 2
On deformed mesh ---- On boundary ---- Over all the model
12

13. Static Case Solution.1 - Von Mises stress (nodal values).2
Figure 3
3D elements: : Components: : All
On deformed mesh ---- On boundary ---- Over all the model
Global Sensors
Sensor Name Sensor Value
Energy 2.495e-005J
13

14. 2.3 TASK 2
 DESIGN 1
Figure 13 Design 1
Figure 14 Deformation of Design 1
14

15. Figure 15 Von-mises stress of Design 1
Figure 16 Translational displacement of Design 1
15

16. Figure 17 Principle stress of Design 1
 DESIGN 2
Figure 18 Design 2
16

17. Figure 19 Deformation of Design 2
Figure 20 Von-mises stress of Design 2
17

18. Figure 21 Translational displacement of Design 2
Figure 22 Principle stress of Design 2
18

19.  DESIGN 3
Figure 23 Design 3
Figure 24 Deformation of Design 3
19

20. Figure 25 Von-mises stress of Design 3
Figure 26 Translational displacement of Design 3
20

21. Figure 27 Principle stress of Design 3
21

22. 2.4 MORPHOLOGICAL CHART
DESIGN Original beam Design 1 Design 2 Design 3
A (mm) 25 25 25 25
B (mm) 20 20 20 20
w (N/m) 1500 1500 1500 1500
Poisson’s 0.29 0.29 0.29 0.29
ratio (v)
Em (GPa) 200 200 200 200
Es (MPa) 400 400 400 400
Von Misses 8.32x107 9.89x107 2.82x107 1.26x107
Stress (Nm2)
Translational 0.000426 0.000507 0.000644 0.000277
Displacement
(mm)
Principal 1.09x107 1.31x107 1.91x107 1.07x107
Stress (Nm2)
22

23. 3.0 DISCUSSION
From the analysis above, I had done the finite element analysis (FEA) for original
just in 3D. The Von-Mises Stress obtained is 8.32 x107 Nm2 , Translational displacement is
0.000426 mm, and Principle Stress is 1.09x107 Nm2 for 3D beam by using CATIA.
A beam is a structural element that is capable of withstanding load primarily by
resisting bending. The bending force induced into the material of the beam as a result of the
external loads, own weight, span and external reactions to these loads is called a bending
moment. In order to increase the stiffness of the bracket without compromising the
dimensions, we have to design 3 concepts to overcome the problem. However, only one out
from three of my design was successfully done. By increasing the stiffness of the beam, the
deflection of the rectangular support bracket must be reduced.
From the result obtained, the 1st design introduced us a poor result than the original
beam. The value of Von Misses Stress = 9.89x107 Nm2, Translational Displacement =
0.000507 mm and Principal Stress= 1.31x107Nm2. All the value is much greater than the
original beam, thus this design cannot promote to increase the stiffness of the bracket.
For the 2nd design, the value of the Von Misses Stress = 2.82x107 Nm2, Translational
Displacement = 0.000644 mm and Principal Stress = 1.91x107x107 Nm2. This design also
gives the poor result than the original beam and design 1.
However, the third design was successfully obtained the exact value to increase the
stiffness due to its value for Von Misses Stress = 1.26 x107 Nm2, Translational
Displacement = 0.000277 mm and Principal Stress = 1.07x107 Nm2. This design is the best
among the other design because have less value than the original beam. So, this design can
be promote to increase the stiffness and reduced the deflection.
23

24. 4.0 CONCLUSIONS
As the conclusion, based on the translational displacement, the best design goes to the
rd
3 design; where the translational displacement of the beam is smaller than the original beam
which is 0.000277 mm rather than 0.000426 mm. Thus this design can overcome the
problem.
5.0 APPENDIX
(a) ADDITIONAL STRESS CONTOUR PLOT
The program provides two types of stress contour plots: a von Mises-Hencky effective
stress plot and a Factor of Safety on Material Yield plot. In both of these plots the
maximum stress plotted is limited to the yield strength of the cable component. Thus,
where stress concentrations occur, the maximum stress reported by the program will
never exceed the yield strength.
The following stress contours are available:
1. Stress xx - contour;
2. Stress yy - contour;
3. Stress xy - contour;
4. Stress zz - contour;
5. Major Principal - contour;
6. Minor Principal - contour;
7. Stress 1/ Stress 3 - contour;
8. Max. Shear - contour;
9. P - mean stress. contour;
10. q - shear stress. is the second stress invariants;
11. q/p - ratio of q/p as defined above;
12. Pore pressure - pore water pressure;
13. Yield zone - PISA actually plots the the value of the yield zone function f for
plastic models.
24

25. (b) REFERENCES
i. http://en.wikipedia.org/wiki/Beam_(structure)
ii. http://en.wikipedia.org/wiki/Finite_element_analysis
iii. http://answers.yahoo.com/question/index?qid=20081120131225AAbKEvM
iv. http://www.newport.com/Fundamentals-of
Vibration/140234/1033/content.aspx
v. http://cedb.asce.org/cgi/WWWdisplay.cgi?115570
25