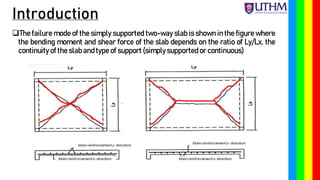
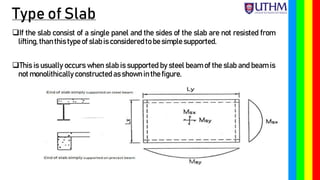
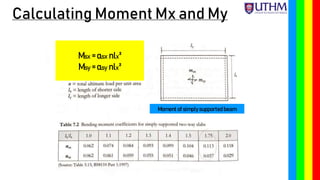
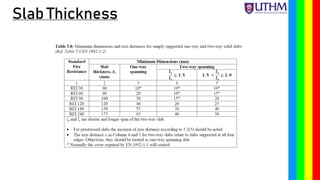
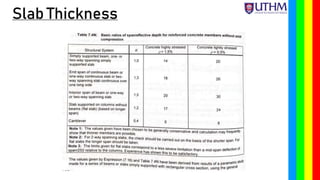
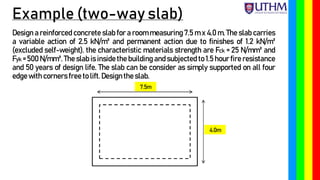
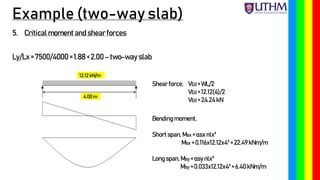
Chapter 6 discusses the design principles of two-way reinforced concrete slabs, focusing on their reinforcement in both directions when supported on all four edges. An example is provided for designing a slab with specific measurements and loads, including calculations for moment, shear force, and reinforcement requirements. Key factors such as minimum thickness, durability, and fire resistance are also considered in the design process.

1. CHAPTER 6
DESIGN OF
REINFORCED
CONCRETE SLAB (TWO-
WAY SLAB)

2. Introduction
In two-way slab, the reinforcement is designedon both directions.
The condition occurs when the slab is supported on all four edge and the ratio of
longer span to shorter span less than 2.
one-way slab two-way slab

3. Introduction
The failure mode of the simply supported two-way slab is shown in the figure where
the bending moment and shear force of the slab depends on the ratio of Ly/Lx, the
continuity of the slab andtype of support (simplysupported or continuous)

4. Type of Slab
If the slab consist of a single panel and the sides of the slab are not resisted from
lifting, than this type of slab is consideredto be simple supported.
This is usually occurs when slab is supported by steel beam of the slab and beam is
not monolithically constructed as shown in the figure.

5. Calculating Moment Mx and My
Moment of simplysupported beam
Msx = αsx nlx²
Msy = αsy nlx²

6. Slab Thickness

7. Slab Thickness

8. Example (two-way slab)
Design a reinforced concrete slab for a room measuring 7.5 m x 4.0 m. The slab carries
a variable action of 2.5 kN/m² and permanent action due to finishes of 1.2 kN/m²
(excluded self-weight). the characteristic materials strength are Fck = 25 N/mm² and
Fyk = 500 N/mm². The slab is inside the building and subjected to 1.5 hour fire resistance
and 50 years of design life. The slab can be consider as simply supported on all four
edgewith corners free to lift. Designthe slab.
7.5m
4.0m

9. Example (two-way slab)
1. Specification
Permanent action Gk = 1.20 kN/m² (Excludeds-w)
Variable action, QK = 2.50 kN/m²
Strength of concrete = 25 N/mm²
Strength of steel = 500 N/mm²
Fire resistance = 1.5 hours
Exposure Classes = XC1
Assume:
Øbar = 10mm

10. Example (two-way slab)
2. Slab thickness
Minimum thicknessfor fire resistance= 100 mm (Table5.8EN1992.1.2)
Estimatedthickness consideringdeflection control, h = Lx/20
h = 4000/20 mm
use h = 200 mm

11. Example (two-way slab)
3. Assessdurability requirement, fire andbond
Min. coverwithregardto bond, Cmin,b - 10 mm (table 4.2)
Min. cover withregardto durability,Cmin,dur - 10 mm (table 4.4N)
Min. Requirementaxis distancefor R60 fire - a= 20mm (table 5.8 EN1992.1.2)
Min. cover withregardto fire,Cmin, - a – Øbar/2
- 20mm- 10mm/2= 15 mm
Allowable in designfor deviation,∆Cdev - 10 mm (BS EN 1992-1-1- 4.4.1.3)
Nominal Cover,Cnom - Cmin(a)+ ∆Cdev= 20mm + 10 mm = 30 mm
use Cnom = 30 mm

12. Example (two-way slab)
4. Assessaction on slab
Slab self-weight 0.200 x25 = 5.00 kN/m²
Permanent loading (excludingself-weight) = 1.20 kN/m²
Permanent action, GK = 6.20 kN/m²
Variable action, Qk = 2.50 kN/m²
Designaction = 1.35 Gk+ 1.50 Qk
= 1.35(6.20)+ 1.50(2.50)
= 12.12 kN/m²
Consider 1m width = 12.12 x 1m = 12.12 kN/m

13. Example (two-way slab)
5. Critical moment and shear forces
Ly/Lx= 7500/4000 = 1.88 < 2.00 – two-way slab
12.12 kN/m
4.00 m
Shear force, VEd = WL/2
VEd = 12.12(4)/2
VEd = 24.24kN
Bendingmoment,
Short span, Msx = αsxnlx²
Msx = 0.116x12.12x4²= 22.49kNm/m
Longspan,Msy = αsy nlx²
Msy = 0.033x12.12x4²= 6.40 kNm/m

14. Example (two-way slab)
6. Designof main reinforcement
Effective depth, dx = h – Cnom – Øbar/2 = 200 – 30 – (10/2) = 165 mm
Effective depth, dy = h – Cnom – 1.5Øbar = 200 – 30 – (1.5x10) = 155 mm

15. Example (two-way slab)
6. Designof main reinforcement
ShortSpan:
Mbal = 0.167 fck bd²
Mbal = 0.167(25)(1000)(165²)
Mbal = 114kNm > M = 22.49kNm
As = M As = 22.49x10^6
0.87 fykZ 0.87(500)(0.95x165)
Asreq = 329mm²/m
Provide H10-225(Asprov = 349 mm²/m)
compression reinforcement is not required
use z = 0.95d

16. Example (two-way slab)
6. Designof main reinforcement
LongSpan:
Mbal = 0.167 fck bd²
Mbal = 0.167(25)(1000)(155²)
Mbal = 100kNm > M = 6.40kNm
As = M As = 6.40 x 10^6
0.87 fykZ 0.87(500)(0.95x155)
Asreq = 100 mm²/m
Provide H10-300 (Asprov = 262 mm²/m)
compression reinforcement is not required
use z = 0.95d

17. Example (two-way slab)
6. Designof main reinforcement
Calculate minimum and maximum
Asmin = 0.0015 bd
Asmin = 0.0015(1000)(165)
= 248 mm²/m
Asmax = 0.04 Ac
Asmax = 0.04 (1000x200)
= 8000 mm²/m

18. Bar Reinforced Concrete (BRC)

19. THANK YOU