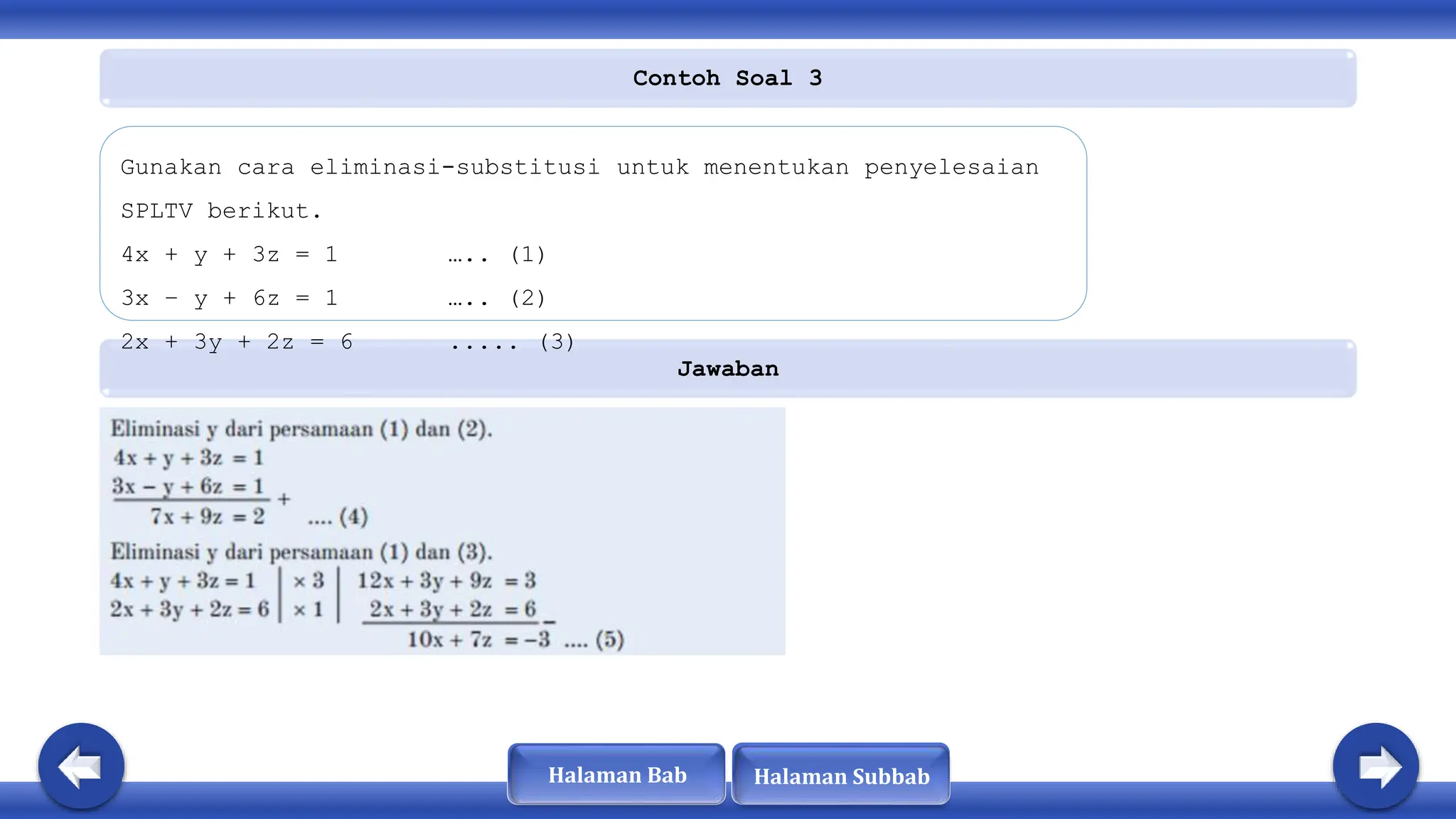
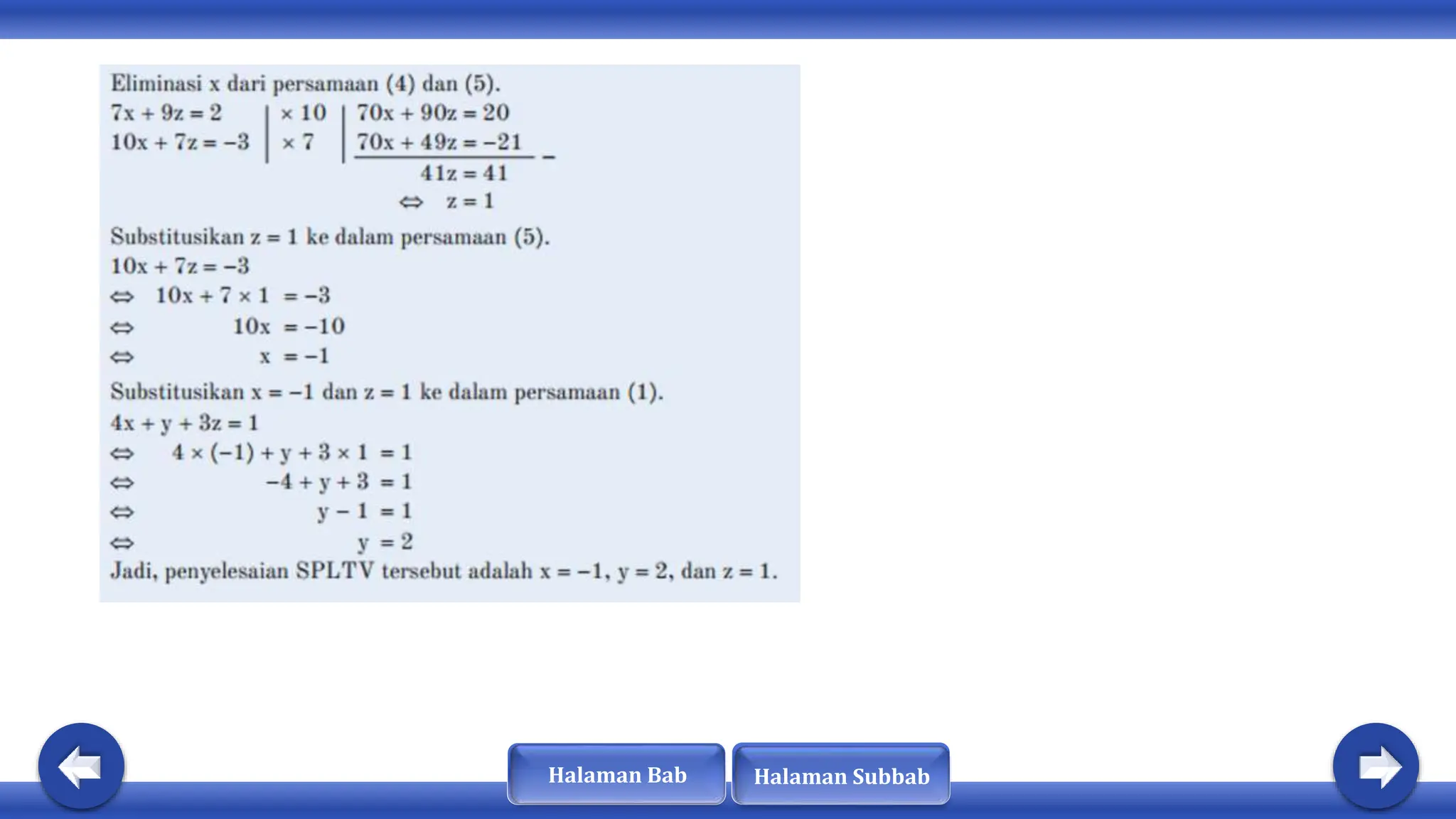
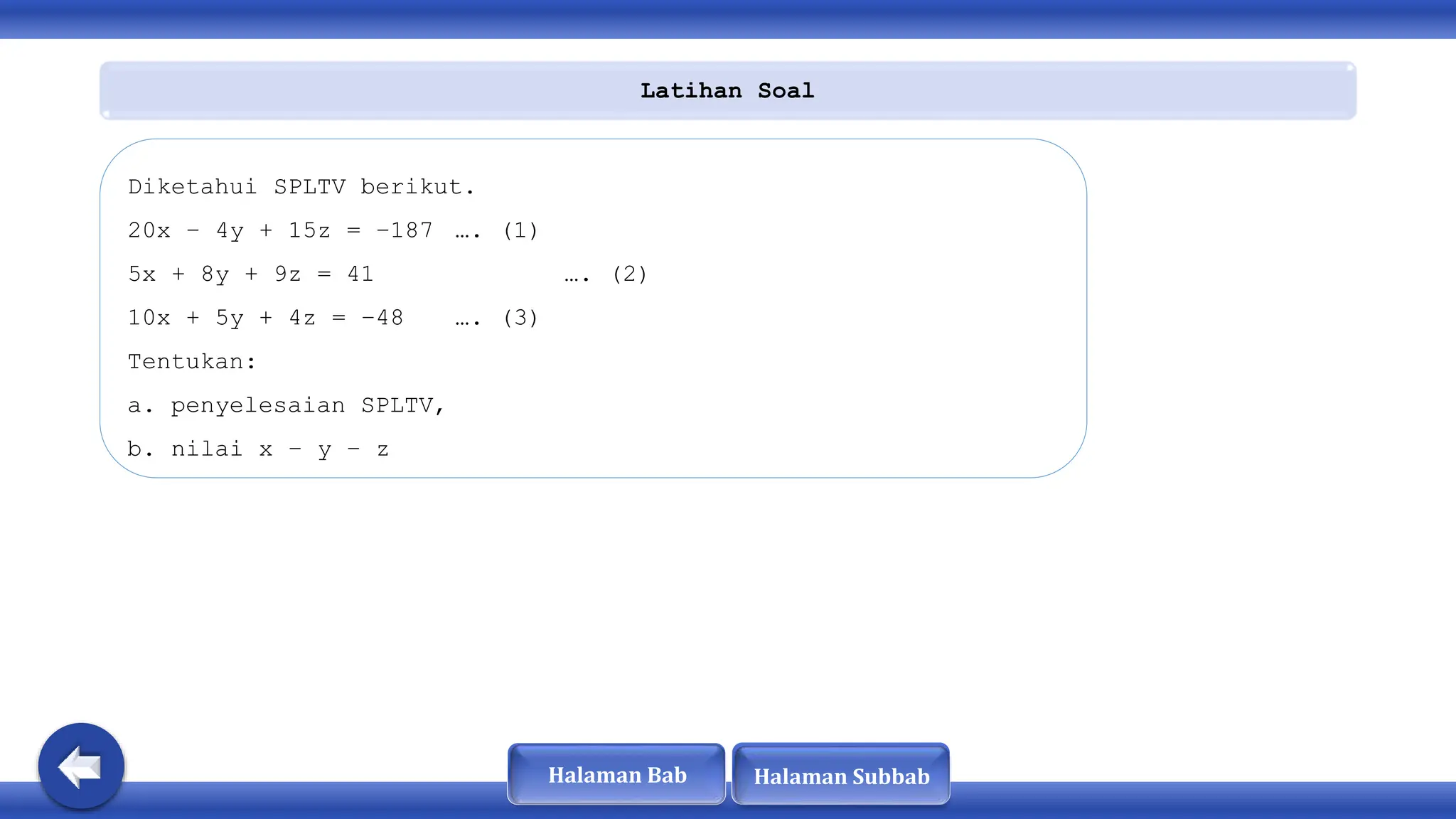
Dokumen ini membahas tentang sistem persamaan linear tiga variabel (SPLTV), termasuk konsep, bentuk, dan metode penyelesaian seperti eliminasi dan substitusi. SPLTV terdiri dari persamaan yang saling berkaitan dan dapat dikategorikan menjadi homogen dan tidak homogen berdasarkan nilai konstanta. Selain itu, dokumen memberikan contoh soal dan langkah-langkah penyelesaian yang berkaitan dengan SPLTV.

1. BAB
III
Sistem Persamaan Linear
Sistem Persamaan Linear Tiga
Variabel (SPLTV)

2. A. Sistem Persamaan Linear Tiga Variabel (SPLTV)
1. Mengingat Kembali Konsep Sistem Persamaan Linear Dua Variabel
2. Bentuk Sistem Persamaan Linear Tiga Variabel
3. Penyelesaian Sistem Persamaan Linear Tiga Variabel
Halaman Bab
4. Menyelesaikan Sistem Persamaan Linear Tiga Variabel
5. Menyelesaikan Masalah yang Berkaitan Dengan Sistem Persamaan Linear Tiga
Variabel

3. APA ITU PERSAMAAN LINEAR ?

4. PERSAMAAN LINEAR ADALAH persamaan yang mengandung variabel
berpangkat satu. Persamaan ini disebut juga dengan persamaan
berderajat satu (persamaan linear satu variabel).

7. Halaman Bab
1. Mengingat Kembali Konsep Sistem Persamaan Linear Dua Variabel (SPLDV)
Halaman Subbab
a. Konsep Sistem Persamaan Linear Dua Variabel
Sistem persamaan linear dua variabel (SPLDV) terdiri atas
beberapa persamaan linear dua variabel yang saling berkaitan.
Bentuk umum SPLDV:
ax + by = c ….. (1)
dx + cy = e ….. (2)
b. Cara Menyelesaikan Sistem Persamaan Linear Dua Variabel
SPLDV dapat diselesaikan dengan cara atau metode grafik,
eliminasi, substitusi, dan eliminasi-substitusi.

8. Contoh Soal
Halaman Bab Halaman Subbab

9. Contoh Soal
Halaman Bab Halaman Subbab

10. Latihan Soal
Tentukan penyelesaian SPLDV berikut.
x + 3y = 10 ….. (1)
2x – y = -1 ….. (2)
Halaman Bab Halaman Subbab

11. 2. Bentuk Sistem Persamaan Linear Tiga Variabel
Sistem persamaan linear tiga variabel (SPLTV) terdiri atas
beberapa persamaan linear tiga variabel yang saling
berkaitan. Bentuk umum SPLTV:
a1x + b1y + c1z = d1 ….. (1)
a2x + b2y + c2z = d2 ….. (2)
a3x + b3y + c3z = d3 ..... (3)
Jika d1, d2, dan d3 bernilai nol, SPLTV dinamakan sistem
persamaan linear homogen. Jika d1, d2, atau d3 tidak bernilai
nol, SPLTV dinamakan sistem persamaan linear tidak homogen
(nonhomogen).
Halaman Bab Halaman Subbab

12. Menyelesaikan Sistem Persamaan Linear Tiga Variabel
Penyelesaian SPLTV dapat ditentukan dengan cara eliminasi, substitusi, dan
gabungan eliminasi-substitusi.
Cara atau metode eliminasi adalah cara menyelesaikan SPLTV dengan menghilangkan
dua variabel hingga nilai salah satu variabel dapat ditentukan. Selanjutnya
langkah serupa dilakukan sehingga semua nilai variabel diperoleh.
Halaman Bab Halaman Subbab

13. Cara substitusi adalah cara menyelesaikan SPLTV dengan didahului mengubah salah
satu variabel menjadi bentuk variabel lainnya (bentuk eksplisit). Selanjutnya
bentuk eksplisit yang diperoleh disubstitusikan ke persamaan anggota SPLTV. Untuk
lebih jelasnya, perhatikan contoh soal pada uraian selanjutnya.
Halaman Bab Halaman Subbab

14. Cara eliminasi-substitusi adalah cara menyelesaikan SPLTV dengan menghilangkan
dua variabel hingga nilai salah satu variabel dapat ditentukan. Selanjutnya nilai
yang diperoleh disubstitusikan sehingga semua nilai variabel diperoleh. Cara atau
metode eliminasi adalah cara menyelesaikan SPLTV dengan menghilangkan dua
variabel hingga nilai salah satu variabel dapat ditentukan. Selanjutnya langkah
serupa dilakukan sehingga semua nilai variabel diperoleh.
Halaman Bab Halaman Subbab

15. Contoh Soal 1
Jawaban
Diketahui sistem persamaan berikut.
3x + y + 3z = 16 ….. (1)
4x + 2y + 3z = 19 ….. (2)
5x + 3y + 2z = 19 ..... (3)
Gunakan cara eliminasi untuk menentukan penyelesaian SPLTV
tersebut.
Halaman Bab Halaman Subbab

16. Halaman Bab Halaman Subbab

17. Halaman Bab Halaman Subbab

18. Contoh Soal 2
Jawaban
Gunakan cara substitusi untuk menentukan penyelesaian SPLTV
berikut.
2x + 3y + z = 6 ….. (1)
x + 4y + 3z = 13 ….. (2)
4x – y + 2z = 12 ..... (3)
Halaman Bab Halaman Subbab

19. Halaman Bab Halaman Subbab

20. Contoh Soal 3
Jawaban
Gunakan cara eliminasi-substitusi untuk menentukan penyelesaian
SPLTV berikut.
4x + y + 3z = 1 ….. (1)
3x – y + 6z = 1 ….. (2)
2x + 3y + 2z = 6 ..... (3)
Halaman Bab Halaman Subbab

21. Halaman Bab Halaman Subbab

22. Latihan Soal
Diketahui SPLTV berikut.
20x – 4y + 15z = –187 …. (1)
5x + 8y + 9z = 41 …. (2)
10x + 5y + 4z = –48 …. (3)
Tentukan:
a. penyelesaian SPLTV,
b. nilai x – y – z
Halaman Bab Halaman Subbab

23. 5. Menyelesaikan Masalah yang Berkaitan Dengan Sistem Persamaan Linear Tiga Variabel
Untuk menyelesaikan masalah yang berkaitan dengan SPLTV, dilakukan langkah-
langkah berikut.
a. Memisalkan nilai yang belum diketahui menjadi variabel.
Variabel digunakan untuk mewakili nilai yang belum diketahui. Variabel yang
digunakan misalnya x, y, dan z.
b. Menyusun model matematika berbentuk SPLTV.
Cermati permasalahan yang disajikan kemudian bentuklah persamaan-persamaan
linear anggota SPLTV.
c. Menyelesaikan SPLTV.
Tentukan penyelesaian SPLTV sehingga nilai variabel-variabel dapat ditemukan.
d. Menafsirkan penyelesaian SPLTV sesuai dengan permasalahan semula.
Cocokkan nilai variabel yang telah ditemukan dengan nilai yang diwakilinya.
Selanjutnya gunakan nilai-nilai tersebut untuk menyelesaikan masalah yang
ditanyakan. Halaman Bab Halaman Subbab

24. Contoh Soal
Jawaban
Sebuah koperasi sekolah menjual 3 jenis paket alat tulis. Paket 1
berisi 1 pensil, 2 bolpoin, dan 3 buku tulis serta dijual seharga
Rp16.900,00. Paket 2 berisi 2 pensil, 2 bolpoin, 4 buku tulis serta
dijual seharga Rp22.200,00. Paket 3 berisi 3 pensil, 4 bolpoin, dan
5 buku tulis. Harga paket 3 sebesar Rp33.500,00. Berapakah harga 1
pensil?
Halaman Bab Halaman Subbab

25. Halaman Bab Halaman Subbab