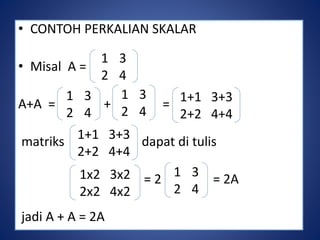
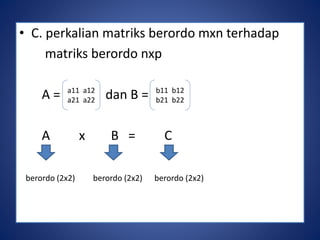
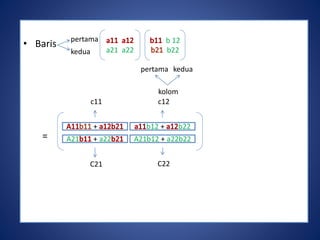
Dokumen tersebut membahas tentang perkalian matriks terhadap skalar dan perkalian dua matriks. Perkalian matriks terhadap skalar dilakukan dengan mengalikan setiap komponen matriks dengan bilangan real. Perkalian dua matriks dilakukan dengan mengalikan baris pertama matriks pertama dengan kolom pertama matriks kedua, dan seterusnya.

1. KELOMPOK 3
DISUSUN OLEH
GALIH SURYANTO PUTRA (14)
ABYADL AMRULAH (01)
IMAM WAHYUDI (16)
WAHYU PRATAMA ADITYA ()

2. 3-4 PERKALIAN MATRIKS TERHADAP
SKALAR
Sebuah matriks dapat dikalikan dengan
skalar (bilangan real) dengan cara
mengalikan setiap komponen matriks
dengan skalar. Misal matriks A dikali
dengan skalar k maka komponen
matriks A dikali dengan k

3. • Perkalain skalar
• K x a b =
c d
ka kb
kc kd

4. • CONTOH PERKALIAN SKALAR
• Misal A =
1 3
2 4
A+A = + =
1+1 3+3
2+2 4+4
matriks dapat di tulis
= 2 = 2A
jadi A + A = 2A
1 3
2 4
1+1 3+3
2+2 4+4
1 3
2 4
1x2 3x2
2x2 4x2
1 3
2 4

5. • Contoh perkalain skalar
• jika B =
4 6
-2 10
½x4 ½x6
½x(-2) ½x10
• Maka ½B = =
• Maka -3B = =
2 3
-1 5
-3x4 -3x6
-3x(-2) -3x10
-12 -18
6 -30

6. • SIFAT SIFAT: perkalian suatu matriks dengan
real(skalar)
• Misalkan p dan q adalah bilangan real, A dan B
adalah matriks - matriks berordo m x n
• (a) (p + q).A = pA + qA
• (b) p(A + B) = pA + qB
• (c) p(q.A) = (p . q).A
• (d) 1 . A = A . 1 =A
• (e) (-1)A = A(-1) = -A

7. 3-5 PERKALIAN DUA MATRIKS
• Perkalian matriks yaitu mengalikan setiap
elemen baris pada matriks yang pertama
dengan elemen elemen kolom pada matriks
yang kedua, lalu hasilnya di jumlahkan.
• Memiliki syarat mxn nxp dan menghasilkan
mxp
• Jadi sayaratnya n kolom pada matriks satu
harus = n baris matriks kedua
• n=n

8. • 3-5-1 perkalian matriks berordo m x n
t terhadap matriks berordo n x 1
• A. perkalian matriks dengan berordo 1 x n
terhadap matriks n x 1
A = ( a11 , a12 , a13 , … , a1n) dengan
matriks 1 x n
B11
B21
…
Bn1
B = dengan matriks n x 1

9. • Jika c adalah matriks hasil perkalian matriks A
terhadap matriks B atau C = AB, maka
• Matriks C berordo 1x1, dalam hal ini C adalah
sebuah skalar
• Matriks C ditentukan oleh
C= (a11b11+a12b21+a13b31+ … +a1n bn1)

10. • Contoh
4 2 3
• Jika A = jika B =
1
• AB = 4 2
= (4x3 + (-2)x1) = 10
3
1

11. • B. perkalian matriks berordo m x n terhadap
matriks berordo n x 1
A= B =
C =
a11 a12 a13 … a1n
a21 a22 a23 … a2n
a31 a32 a33 … a3n
… … … … …
Am1 am2 am3 … amn
B11
B21
B31
…
Bn1
A11b11 + a12b21 + a13b31 + … + a1n bn1
A21b11 + a22b21 + a23b31 + … + a2n bn1
A31b11 + a32b21 + a33b31 + … + a3n bn1
… + … + … + … + …
Am1b11 + am2b21 + am3b31 + … + amnbn1

12. • Contoh
3 2
-4 6
• Jika A = dan B =
-4
8
3 2
-4 6
-4
8
3x(-4) + 2x8
(-4)x(-4) + 6x8
• AB = = =
4
64

13. • C. perkalian matriks berordo mxn terhadap
matriks berordo nxp
a11 a12
a21 a22
A = dan B =
b11 b12
b21 b22
A x B = C
berordo (2x2) berordo (2x2) berordo (2x2)

14. • Baris
=
a21 a22
pertama
kedua
b 12
b22
pertama kedua
kolom
c11 c12
+ b12 + b22
A21 + a22 A21b12 + a22b22
C21 C22

15. • 1. elemen baris pertama kolom pertama matriks
C diperoleh dengan mengalikan tiap elemen pada
baris pertama matriks yang kiri dengan elemen-elemen
yang bersesuaian pada kolom pertama
matriks yang kanan, dan kemudian hasilnya
dijumlahkan.
Jadi, c11 = a11.b11 + a12.b21
• 2. elemen baris pertama kolom kedua matriks C
diperoleh dengan mengalikan tiap elemen pada
baris pertama matriks yang kiri dengan elemen-elemen
yang bersesuaian pada kolom kedua
matriks yang kanan, dan kemudian hasilnya
dijumlahkan.
Jadi , c12 = a11.b12 + a12.b22

16. • 3. elemen baris kedua kolom pertama matriks C
diperoleh dengan mengalikan tiap elemen pada
baris kedua matriks yang kiri dengan elemen-elemen
yang bersesuaian pada kolom pertama
matriks yang kanan, dan kemudian hasilnya
dijumlahkan.
Jadi, c21 = a21.b11 + a22.b12
• 4. elemen baris kedua kolom kedua matriks C
diperoleh dengan mengalikan tiap elemen pada
baris kedua matriks yang kiri dengan elemen-elemen
yang bersesuaian pada kolom kedua
matriks yang kanan, dan kemudian hasilnya
dijumlahkan.
Jadi, c22 = a21.b12 + a22.b22

17. • Contoh
• A= dan B =
4 -6
2 7
1 0
0 1
4 -6
2 7
1 0
0 1
4+0 0-6
2+0 0+7
• AB= = =
4 -6
2 7

18. PEMBAHASAN SOAL

19. Diketahui 3A =
6 -3 0
9 -6 12
-3 -9 15
Dengan 1/3.3.A=A.1=A
6 -3 0
9 -6 12
-3 -9 15
A = 1/3(3A)= 1/3 =
2 -1 0
3 -2 4
-1 -3 5

20. • A = dan B =
dengan ordo A 3x1 dan B 1x3 dan akan
menghasilkan C 3x3
AB =
3
1
2
4 2 1
3x4 3x2 3x1
1x4 1x2 1x1
2x4 2x2 2x1

21. • Jika A = dan B =
1 2 -3
6 -5 4
• AB = =
2
-1
5
1 2 -3
6 -5 4
2
-1
5
1x2 + 2x(-1) + (-3)x5
6x2 + (-5)x(-1) + 4x5

22. 1 -1
2 0
• A = dan B =
• Tentukan AB dan AB transpos
• AB = = =
• Transpos AB =
3 -1
2 1
1 -1
2 0
3 -1
2 1
1x3+(-1)x2 1x(-1)+(-1)x1
2x3+0x2 2x(-1)+0x1
1 -2
6 -2
1 6
-2 -2