Fundamental Power System

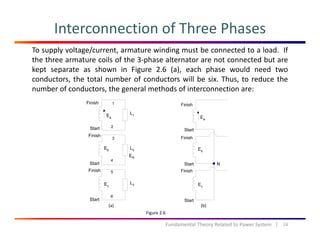
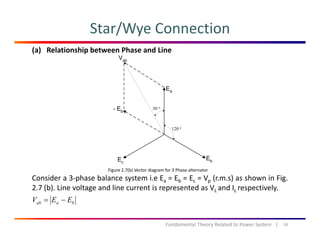
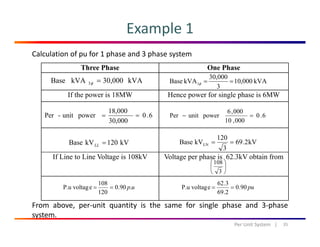
REVISION ON FUNDAMENTALREVISION ON FUNDAMENTAL
THEORY RELATED TO POWER
SYSTEM

Complex Power
• If voltage and current are known, complex power can be
calculated. Suppose voltage and current through a load or a
circuit are given bycircuit are given by
and
• Complex power is given by:
β∠= IIα∠= VV
p p g y
S i l f d t
βα −∠×== IVVIS * (2.1)
• S is also referred as apparent power.
θθ sincos IVjIVS += (2.2)
)sin()cos( βαβα −+−= IVjIVS
QjPS +=
(2.3)
Where is the angle between voltage and current.
2Fundamental Theory Related to Power System |
βαθ −=

Complex Power
• The real part of equation i.e P is real power and the imaginary part
is reactive power, Q. The Unit for P is watt or MWatt, and for Q Var
or MVar. Cosine θ is known as power factor. Equation 2.3 can beor MVar. Cosine θ is known as power factor. Equation 2.3 can be
represented in a vector form:
θ
Figure 2.1 Phasor diagram
IVIVIVQPS =+=+= 2222
)sin()cos( θθ (2.4)
• From the diagram, , power factor :PQ /tan =θ
)/(tancoscos 1
PQ−
=θ 22
cos
QP
P
+
=θ(2.5) (2.6)
QP +

Complex Power
• For a simple circuit that consists of an element Z = R + jX,
we can substitute into Equation (2.3), to yield:ZIV =
θcos
2
ZIP = θsin
2
ZIQ =(2.7) (2.8)
• It is known that and , therefore :θcosZR = θsinZX =
RIP
2
= XIQ
2
=(2.9) (2.10)

Example
Two ideal voltage source machines 1 and 2 are connected as shown in the Fig.
2.2. If V, V, and . Determine
(a) Which machine generate or absorb power and the amount
°∠= 01001E °∠= 301002E Ω+= 50 jZ
( ) g p
(b) Whether each machine receive or supply reactive power and the what is
the amount
(c) Active and reactive power absorb by the impedance(c) Active and reactive power absorb by the impedance.
Figure 2.2

Example (cont.)
Solution:
)506.86(010021 jjEE
I
+−+
=
−
=
5
21
jZ
I ==−
°∠=−−=
−
= 19535.1068.210
504.13
j
j
5
j
j
2681000)68.210(100*121 jjIES +−=+−==−
68.210
5
100)506.86(12
12 j
j
j
Z
EE
I +=
−+
=
−
=−
2681000)68.210)(506.86(*212 jjjIES +=−+==−
Total Power absorb by impedance: VarXI 53653510 22
=×=
Total Power absorb by impedance: VarXI 536535.10 =×=

Example (cont.)
Solution (cont.):
According to solution of power flow from Machine 1 to Machine
( ) d h h b b2 ( S1‐2), P is negative and Q is positive. Thus, machine 1 absorbs
energy with the rate of 1000 W and supply reactive power of 268
Var. Machine 1 is a motor.
According to solution of power flow from Machine 2 to Machine
1 ( S2‐1), P is positive and Q is positive. Thus, Machine 2 is a
generator that generates 1000 W and supply reactive power of
268 Var. All the active power P generated by Machine 2 isp g y
transferred to Machine 1.

Three Phase System
Three‐phase system is widely being used in industry as
compared to single phase system. There are few reasons such as:compared to single phase system. There are few reasons such as:
1. Power and torque in a 3 phase motor and generator is
constant as compared to single phase machine, which the
i ib i d bl h ftorque is vibrating double the system frequency.
2. Three phase machine produces huge power.
3 Transmission system based on three phase system able to3. Transmission system based on three phase system able to
deliver more power ac compared single phase system.

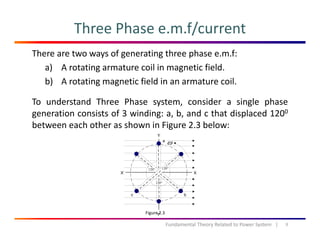
Three Phase e.m.f/current
There are two ways of generating three phase e.m.f:
a) A rotating armature coil in magnetic field.
b) A rotating magnetic field in an armature coil.
To understand Three Phase system, consider a single phase
generation consists of 3 winding: a, b, and c that displaced 1200
between each other as shown in Figure 2.3 below:
Y
ωa
°120°120
XX’
bc
120
°120
Y’Figure 2.3

In this position, winding b needs to rotate 120o to be in position a, winding c
needs to rotate 240 o to be in position a. The generated e.m.f can be
represented as follows:
θθ
Figure 2.4
All the generated e.m.f can be written as follows:
tEe mA ωsin= (3.1)(reference)
)120(sin °−= tEe mB ω
)240(sin °−= tEe mC ω )120(sin °+= tEe mC ω
(3.2)
(3.3)
AfA 2h
or
AfNBANBE mmm πω 2==where

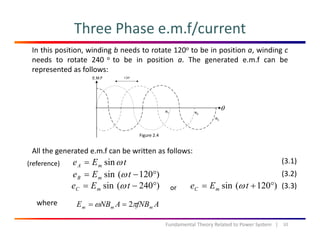
The generated e.m.f is a balance AC voltage because has the same magnitude
and different phase of 120o. e.m.f also can be represented in a vector form as
shown in Fig. 2.5. E is the magnitude of the e.m.f:
Figure 2.5
For a balance three phase e.m.f, it can be shown that the sum of these three
e.m.f is equal to zero:
M th d 1Method 1:
0]60cossin2[sin
]60cos)180(sin2[sin
=°=
°°−+=++
ttE
ttEeee mcba
ωω
ωω
0]60cossin2[sin =−= ttEm ωω

Method 2:
00 jEEEa +=°∠=
120 (0.5 0.866)bE E E j= ∠ − ° = −( )b j
)866.005.0(120240 jEEEEc +−=°∠=°−∠=
0)866.005.0()866.05.0()0( =+−+−−++=++∴ jEjEjEEEE cba

Phase Sequence
• Phase sequence refers to the order in which the three
phases attain their peak or maximum valuesphases attain their peak or maximum values.
• In the generation of e.m.f of Fig. 2.5, the rotation is
assumed to be counter‐clockwise. Thus, phase a attain, p
the first maximum, followed by b and lastly c.
• On the other hand, if the rotation is assumed to be
l k i th h b > > b thiclock‐wise, the phase sequence becomes a‐> c‐> b, this
is called negative phase sequence.
• In three phase system, only these two sequences areIn three phase system, only these two sequences are
possible.

Interconnection of Three Phases
To supply voltage/current, armature winding must be connected to a load. If
the three armature coils of the 3‐phase alternator are not connected but are
kept separate as shown in Figure 2.6 (a), each phase would need two
d h l b f d ill b i Th d hconductors, the total number of conductors will be six. Thus, to reduce the
number of conductors, the general methods of interconnection are:
Figure 2.6
(a) (b)

Star/Wye Connection
In this interconnection, the similar ends say, ‘start’ ends of three coils (it could
be finishing ends also) are joined together at point N as shown in Fig. 2.6 (b).
The point N is known as star point or neutral point. The three conductors
i i N l d b i l d k lmeeting at point N are replaced by a single conductor known as neutral
conductor. Such an interconnected is known as four‐wire 3‐phase system
diagrammatically shown in Fig. 2.7 (a).
Voltage at each coil is called phase voltage and current at the coil is called
phase current Whereas voltage at the terminal is called Line voltage (V ) V
Figure 2.7(a) Star connection for 3 Phase alternator
phase current. Whereas, voltage at the terminal is called Line voltage (VL)‐Vab,
Vac, Vbc, and current at the terminal is called line current (IL).

Star/Wye Connection
(a) Relationship between Phase and Line
Figure 2 7(b) Vector diagram for 3 Phase alternator
Consider a 3‐phase balance system i.e Ea = Eb = Ec = Vp (r.m.s) as shown in Fig.
2.7 (b). Line voltage and line current is represented as VL and IL respectively.
Figure 2.7(b) Vector diagram for 3 Phase alternator
bb EEV −=
baab EEV

Star/Wye Connection
(a) Relationship between Phase and Line (cont.)
Using sin rule,
°
=
° 30i120i
pL
VV
g ,
°° 30sin120sin
2/12/3
pL
VV
=
2/12/3
pL VV 3= (r.m.s)
For the line, it can be seen that IL = Ip
***Note***
• In a practical 3‐phase system, the parameter data for alternator and
motor is referred to the line voltage, unless otherwise stated.
• The above formula is true for a balanced system only.The above formula is true for a balanced system only.

Star/Wye Connection
(b) Power
The total active or true power in the circuit is the sum of the three phase
powers, hence;
It is known that                            and
powerphase×=3poweractiveTotal φcos3 pp IVP ×=or
pL VV 3= Lp II =
Hence, in term if line values,
φcos
3
3 ×××= L
L
I
V
P φcos3 LL IVP =or
Similarly, the total reactive power is given by,
3
φLL
φsin3 LL IVQ =
Note:       is angle between phase voltage and phase current and not between
the line voltage and line current.
IVS 3
φ
The total apparent power of the three phases is:
LL IVS 3=

Delta Connection
For delta connection, the circuit is shown in Fig. 2.8:
The relationship between phase current and line is:
Figure 2.8 Delta interconnection for 3 Phase alternator
Consider the phasor diagram in Fig. 2.7 (b), which can also be used to represent
current. Hence; ab a bI I I= −
=
pL
II
Using sin rule, °
=
° 30sin120sin
2/12/3
pL
II
=
2/12/3
pL II 3= (r.m.s)

Delta Connection
(a) Power
Total active power for star connection is the sum of power on each phase.
φIVhP φ3 IVPT t l
For Delta connection, and
φcospp IVperphaseP = φcos3 pp IVPowerTotal ×=
pL II 3= φcos3 LL IVP =
;
Hence,
φcos
3
3 ×××= L
L
V
I
P φcos3 LL IVP =or
Similary, the total reactive power is given by . The total
apparent power of the three phases is;
φsin3 LL IVQ =
**It can be seen that the equations for power are the same for star
LL IVS 3=
interconnection

Example (Try this now)
A three‐phase line has an impedance of 2 + j4Ω as shown in Figure 1 below.
Ω
Ω
Ω
Ω
Ω
The line feeds two balanced three‐phase loads that are connected in parallel.
Figure 1
The line feeds two balanced three phase loads that are connected in parallel.
The first load is Y‐connected and has an impedance of 30 + j40Ω per phase.
The second load is ∆‐connected and has an impedance of 60 ‐ j45Ω. The line
is energized at the sending end from a three‐phase balanced supply of line
voltage 207.85 V. Taking the phase voltage Van as reference, determine:

Example (cont.)
a) The current, real power and reactive power drawn from the supply.
b) The line voltage at the combined loads.
c) The current per phase in each load.c) The current per phase in each load.
d) The total real and reactive powers in each load and the line.
323121
R
RRRRRR
RA
++
=
BA
RRR
RR
R
++
=1
3R
2
323121
R
RRRRRR
RB
++
=
323121 RRRRRR
R
++
CBA RRR ++
CBA
CA
RRR
RR
R
++
=2
CB RR
R =3
1
323121
R
RC =
CBA RRR
R
++
3

Example (cont.)
Solution:
(a) The current, real power and reactive power drawn from the supply.
The ∆‐connected load is transformed into an equivalent Y. The impedance per
h f h i l Y iphase of the equivalent Y is
Ω−=
−
= 1520
3
4560
2 j
j
Z
The phase voltage is
VV 120
3
85.207
1 ==
The single‐phase equivalent circuit is shown in Figure 2
Ω
Ω
Ω
Ω
Ω
V0120∠
Figure 2

Example (cont.)
Solution:
(a)(cont.):
The total impedance isp
Ω=−++=
−++
−+
++= 2442242
)1520()4030(
)1520)(4030(
42 jj
jj
jj
jZ
With the phase voltage as reference, the current in phase a is
A
V
I 5
01201
=
∠
==
The three‐phase power supplied is
A
Z
I 5
24
p p pp
( )( ) WIVS 180005012033 *
1 =∠∠==

Example (cont.)
Solution:
(b) The line voltage at the combined loads;
The phase voltage at the load terminal isp g
The line voltage at the load terminal is
( )( ) VjjV 3.108.11120110054201202 −∠=−=∠+−∠=
The line voltage at the load terminal is
VVV ab 7.1964.1937.19)8.111(33030 22 ∠=∠=∠=

Example (cont.)
Solution:
(c) The current per phase in each load;
The current per phase in the Y‐connected load and in the equivalent Y of the p p q
∆ load is
Aj
j
j
Z
V
I 4.63236.221
4030
20110
1
2
1 −∠=−=
+
−
==
Th h t i th i i l ∆ t d l d i i i b
Aj
j
j
Z
V
I 56.26472.424
1520
20110
2
2
2 ∠=+=
−
−
==
The phase current in the original ∆‐connected load, i.e., is given by
A
I
Iab 56.56582.2
303
56.26472.4
303
2
∠=
∠
∠
=
∠
=
303303 −∠−∠

Example (cont.)
Solution:
(d) The total real and reactive powers in each load and the line;
The three‐phase power absorbed by each load isp p y
( )( ) var6004504.63236.23.108.11133 *
121 jWIVS +=∠−∠==
( )( ) 900120056264724310811133 *
jWIVS ∠∠
The three‐phase power absorbed by the line is
( )( ) var900120056.26472.43.108.11133 222 jWIVS +=−∠−∠==
It is clear that the sum of load powers and line losses is equal to the power
( ) ( )( ) var30015054233
22
jWjIjXRS LLL +=+=+=
p q p
delivered from the supply, i.e.,
( ) ( ) ( ) var01800300150900120060045021 jWjjjSSS L +=++−++=++

Per Unit Definition
Quantity in per‐unit      =          Actual quantity
Base value of quantity
• Quantity in per‐unit must follow Kirchhoff law and Ohm law. If
q y
this can be done, all circuit analysis technique is applicable.
• The basic quantity in power system is voltage and current. The
relationship between voltage and current is:relationship between voltage and current is:
S=VI*, (3.1) and   impedance,      Z =VI (3.2)
29Per Unit System   |

Per Unit Definition
• This means if we fix S and V, we can find Z and I using basic circuit
law. The chosen base voltage is according to the rating of the
t ftransformer.
T ran sm issio n lin e
Figure 3.1
33/132kV 132/11kV
A B
• In the above figure, base voltage for bus A is 33kV, bus B is
11kV and for transmission line is 132kV.
30Per Unit System |

Per Unit Definition
In power system, per‐unit is used because of the following advantages:
(1) It gives us a clear idea of relative magnitudes of various quantities, such as
voltage, current, power and impedance.
(2) The per‐unit impedance of equipment of the same general type based on
their own ratings fall in a narrow range regardless of the rating of the
equipment. Whereas their impedance in ohms vary greatly with the rating.
(3) The per‐unit values of impedance, voltage and current of a transformer are
the same regardless of whether they are referred to the primary or
secondary side. This is a great advantage since the different voltage levels
disappeared and the entire system reduces to a system of simple impedance.
(4) The per‐unit systems are ideal for the computerized and analysis and
simulation of complex power problems.simulation of complex power problems.
(5) The circuit laws are valid in per‐unit systems, and the power and voltage
equations are simplified since factor of and 3 are eliminated in the per‐unit
systemsystem
31Per Unit System |

Per Unit Definition
General equation to determine the bases:
(i) Single Phase System
LN
1
kVvoltage,base
kVAbase
Acurrent,Base
φ
=
Vvoltage,base
impedanceBase LN
=Ω
(3.3)
(3.4)
Acurrent,base
impedance,Base =Ω
kVAbasekWpower,Base 11 φφ =
MVAbaseMWpowerBase
(3.4)
(3.5)
MVAbaseMWpower,Base 11 φφ =
φ1
2
LN
MVA
)kVvoltage,(base
impedance,Base =Ω
(3.6)
(3.7)
φ1
2
LN
kVAbase
1000)kVvoltage,(base
impedance,Base
×
=Ω
Ωimpedance,actual
elementanofimpedanceunitPer =
(3.8)
(3 9)
32Per Unit System |
Ωimpedance,base
elementanofimpedanceunitPer = (3.9)

Per Unit Definition
General equation to determine the bases:
(ii) Three Phase System
LL
3φ
kVvoltage,base3
kVAbase
Acurrent,Base
×
=
1000)3/kVvoltage,(base
i d
2
LL ×
(3.10)
( )
/3kVAbase
1000)3/kVvoltage,(base
impedanceBase
3
LL
φ
=
kVAbase
1000)kVvoltage,(base
impedanceBase
2
LL ×
=
(3.11)
(3.12)
kVAbase 3φ
MVAbase
)kVvoltage,(base
impedanceBase
3φ
2
LL
= (3.13)
Or in general Eq. (3.13) can be represented as
( )
B
B
B
S
V
Z
2
=
33Per Unit System |

Per Unit Definition
(ii) Three Phase System (cont.)
A minimum of four base quantities are required to completely
define a per‐unit system: volt‐ampere, voltage, current and
impedance Usually the three phase base volt‐ampere (SB inimpedance. Usually, the three phase base volt ampere (SB in
MVA) and the line to line base voltage (VB in kV) are selected.
34Per Unit System |

Example 1
Calculation of pu for 1 phase and 3 phase system
Three Phase One Phase
30 000
If the power is 18MW Hence power for single phase is 6MW
kVA30,000kVABase 3 =φ kVA000,01
3
30,000
kVABase 1 ==φ
6.0
30,000
18,000
powerunit-Per == 6.0
000,10
000,6
powerunitPer =−
120
If Line to Line Voltage is 108kV Voltage per phase is 62.3kV obtain from
kV120kVBase =LL
kV2.69
3
120
kVBase LN ==
⎟
⎠
⎞
⎜
⎝
⎛
3
108
⎠⎝ 3
up.90.0
120
108
eP.u voltag == pu90.0
2.69
3.62
eP.u voltag ==
From above, per‐unit quantity is the same for single phase and 3‐phase
system.
35Per Unit System |

Change of Base
• The impedance of individual generators and transformers, as
supplied by the manufacturer are generally in term of
t it titi b d th i tipercentage or per‐unit quantities based on their own ratings.
• The impedance of transmission lines are usually by their
ohmic values.
• For power system analysis, all impedance must be expressed
on per unit on a common base.
• In order to do this, an arbitrary base for apparent power must
be selected (usually 100MVA). Then, voltage bases must be
determined for the system.determined for the system.
• Once, a voltage base has been selected for a point in the
system, the remaining voltage bases no longer independent;
h d b h fthey are determine by the various transformer turns ratios.
36Per Unit System |

Change of Base
ld
To convert to a new bases value, suppose is the per‐unit
impedance on the power base and the voltage base . Thus,
old
puZ
old
BS old
BV
old
SZ
or
( )2old
B
B
actualold
B
actualold
pu
V
S
Z
Z
Z
Z ==
( )old
V
2
(3.14a)
Expressing Zactual to a new power base and new voltage base, result in
( )
old
B
Bold
puactual
S
V
ZZ = (3.14b)
the new per unit impedance;
( )2new
new
B
actualnew
B
actualnew
pu
V
S
Z
Z
Z
Z == (3.15)
Substitute Zactual in Eq. (3.14b) into (3.15), yields;
( )BB V
2
⎟⎟
⎞
⎜⎜
⎛ old
B
new
Boldnew VS
ZZ (3 16)
37Per Unit System |
⎟⎟
⎠
⎜⎜
⎝
= new
B
B
old
B
Bold
pu
new
pu
VS
ZZ (3.16)

Example 2
The reactance of a generator, X” is given as 0.25 pu based on its
nameplate 18 kV, 500 MVA. Find the new per unit X” using new
bases of 20 kV and 100MVA.
U i (3 16) pu04050
10018
250''
2
=⎟
⎞
⎜
⎛
⎟
⎞
⎜
⎛
=XUsing (3.16), pu0405.0
50020
25.0 =⎟
⎠
⎜
⎝
⎟
⎠
⎜
⎝
=X
Or by changing the given per‐unit into its actual ohms quantity
and divided using the new base,
pu0405.0
100/20
)500/18(25.0
'' 2
2
==X
38Per Unit System |

Per Unit Reactance for Single Phase Transformer
• The leakage resistance and reactance (in ohm) for a
transformer depends whether it is referred to Primary ortransformer depends whether it is referred to Primary or
Secondary. If these values are stated in per‐unit, the base
power is the rating of the transformer.
• Whereas, the referred base voltage could be from the
Primary or secondary. However, the per‐unit values for
transformer is the same regardless the base voltage is
taken from the Primary or Secondarytaken from the Primary or Secondary.
(Attention: If not stated what the referred side, by default, the( , y ,
impedance is always referred to the lower voltage)
39Per Unit System |

Example 3
A single phase transformer has a rating of 110/440 V, 2.5 kVA. The
leakage reactance measured from the low voltage side is 0.06Ω .
Determine the leakage reactance in per‐unit.Determine the leakage reactance in per unit.
Z base referred to low voltage side Ω=
×
= 84.4
5.2
100011.0 2
In pu, puX 0124.0
84.4
06.0
==
If the leakage reactance measured from the high voltage side, the
reactance X is: Ω=⎟
⎠
⎞
⎜
⎝
⎛
= 96.0
110
440
06.0
2
X
Z base referred to high voltage side =
In pu
⎠⎝ 110
puX 01240
96.0
==
Ω=
×
5.77
5.2
1000440.0 2
In pu,
40Per Unit System |
puX 0124.0
5.77
==

Example 3 (cont.)
Note on the relationship between primary and secondary side:
11
N
N
V
V
= 21
N
N
I
I
=(3.17) (3.18)
If the impedance is connected to the secondary,
b d d ( d l ) ( )
22 NV 12 NI
2
2
2
I
V
Z =
( ) ( )
(3.19)
Substituted V2 and I2 (in Eq. 3.17 and 3.18 respectively) into (3.19),
yields
( )
( )
112
2
INN
VNN
Z = (3.20)
Hence, if impedance is measured from primary side,
( ) 121 INN
2
2
2
1
1
1'
2 Z
N
N
I
V
Z ⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
==
Therefore, if impedance connected at the secondary side is referred
to the primary side, it must be multiply to the ratio of primary side
21 ⎠⎝
over secondary side.
41Per Unit System |

Example 4
Consider the following simple power system network:
2
⎟⎟
⎞
⎜⎜
⎛
=
old
B
new
Boldnew VS
ZZ
The three‐phase power and line‐line ratings of the electrical power
system are as follows
⎟⎟
⎠
⎜⎜
⎝
= new
B
old
B
pupu
VS
ZZ
system are as follows:
G1: 60 MVA 20kV X = 9%
T 50 MVA 20/200 kV X 10%T1: 50 MVA 20/200 kV X = 10%
T2: 50 MVA 200/20 kV X = 10%
M : 43.2 MVA 18kV X = 8%M : 43.2 MVA 18kV X 8%
Line: 200kV Z = 120 + j200 Ω
42Per Unit System |

Example 4 (cont.)
Question:
(a) Draw an impedance diagram showing all impedances in per
it 100 MVA b Ch 20 kV th lt bunit on a 100‐MVA base. Choose 20 kV as the voltage base
for generator.
(b) The motor is drawing 45 MVA, 0.80 power factor lagging at a
line‐to‐line terminal voltage of 18 kV. Determine the terminal
l d h i l f f h i i dvoltage and the internal emf of the generator in per unit and
in kV.
43Per Unit System |

Example 4 (cont.)
Solution (a):
The base voltage VBG1 on the LV side of T1 is 20 kV. Hence, the base on
its HV side is: 200 ⎞⎛its HV side is:
This fixes the base on the HV side of T2 at VB2 = 200 kV, and on its LV
kVVB 200
20
200
201 =⎟
⎠
⎞
⎜
⎝
⎛
=
side at
The generator and transformer reactances in per unit on 100 MVA
kVVB 20
200
20
2001 =⎟
⎠
⎞
⎜
⎝
⎛
=
The generator and transformer reactances in per unit on 100 MVA
base is:
100 ⎞⎛ 100 ⎞⎛
G: T2:
T : M:
puX 15.0
60
100
09.0 =⎟
⎠
⎞
⎜
⎝
⎛
=
puX 2.0
100
10.0 =⎟
⎠
⎞
⎜
⎝
⎛
=
puX 2.0
50
100
10.0 =⎟
⎠
⎞
⎜
⎝
⎛
=
puX 150
18100
080
2
=⎟
⎞
⎜
⎛
⎟
⎞
⎜
⎛
=T1: M:
44Per Unit System |
pu.0
50
0.0 ⎟
⎠
⎜
⎝
puX 15.0
202.43
08.0 ⎟
⎠
⎜
⎝
⎟
⎠
⎜
⎝

Example 4 (cont.)
Solution (a)(cont.):
The base impedance for the transmission line is:
)200( 2
The per unit impedance is
Ω== 400
100
)200( 2
BLZ
p p
Line: puj
j
Zline 5.03.0
400
200120
+=⎟
⎠
⎞
⎜
⎝
⎛ +
=
The per unit equivalent circuit is shown below:
45Per Unit System |

Example 4 (cont.)
Solution (b):
The motor complex power in per unit is puSm °∠=
°∠
= 87.3645.0
100
87.3645
and the motor terminal voltage is:
puVm °∠=
°∠
= 090.0
20
018
20
puI °−∠=
°∠
°−∠
= 87.365.0
09.0
87.3645.0
Thus, the generator line‐to‐line terminal voltage is
pujVg °∠=°−∠++°∠= 82.1131795.1)87.365.0)(9.03.0(09.0
kVVg 359.26)20(31795.1 ==
pujEg °∠=°−∠++°∠= 88.13375.1)87.365.0)(05.13.0(09.0
Thus, the generator line‐to‐line internal emf is:
46Per Unit System |
kVEg 5.27)20(375.1 ==

Example 5
A simple power system consisting of one synchronous generator and
one synchronous motor connected by two transformers and a
transmission line is shown in Fig. 3. Create per phase, per unit circuittransmission line is shown in Fig. 3. Create per phase, per unit circuit
for this power system using a base apparent power of 100 MVA and a
base line voltage at generator G1 of 13.8 kV.
Figure 3
47Per Unit System |
g

Example 5 (cont.)
Solution:
To create a per‐phase, per unit equivalent circuit, we must first
calculate the impedances of each component in the power system incalculate the impedances of each component in the power system in
per‐unit to the system base. The system base apparent power is
SB=100 MVA everywhere in the power system. The base voltage in the
three regions will vary as the voltage ratios of the transformers thatthree regions will vary as the voltage ratios of the transformers that
delineate the regions. The base voltages are:
Region 1: Vbase,1 = 13.8 kV
Region 2: Vbase,2 = Vbase,1 = 110 kV⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
kV
kV
8.13
110
Region 3: Vbase,3 = Vbase,2 = 13.2 kV⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
kV
kV
120
4.14
48Per Unit System |

Example 5 (cont.)
Solution:
The corresponding base impedances in each region are:
R i 1 Z ( ) ( )
2 2
13 8V kVRegion 1: Zbase,1 =
Region 2: Zbase 2 =
( ) ( ),
3 ,
13.8
1.904
100
LL base
base
V kV
S MVAϕ
= = Ω
( ) ( )
2 2
, 110
121
LL baseV kV
= = Ωg base,2
Region 3: Zbase,2 =
3 ,
121
100baseS MVAϕ
= = Ω
( ) ( )
2 2
,
3
13.2
1.743
100
LL base
b
V kV
S MVAϕ
= = Ω
The per‐unit impedance for each component:
G1: Unchanged R = 0.1 pu, X = 0.9 pu
3 , 100baseS MVAϕ
G1: Unchanged R 0.1 pu, Xs 0.9 pu
T1: Unchanged R = 0.01 pu, Xs = 0.05 pu
L : R = X =pu1240
15
=
Ω
pu620
75
=
Ω
L1: RL = , XL =
49Per Unit System |
pu124.0
121Ω
pu62.0
121Ω

Example 5 (cont.)
Solution:
T2: The impedance of T2 is specified in per‐unit on a base of 14.4kV
and 50 MVA in region 3 Therefore the per‐unit resistances andand 50 MVA in region 3. Therefore, the per‐unit resistances and
reactance of this component on the new system base is:
( ) pu
MVAkV
R 238.0
1004.14
01.0
2
=⎟⎟
⎞
⎜⎜
⎛
⎟⎟
⎞
⎜⎜
⎛
= ( ) p
MVAkV 502.13 ⎟
⎠
⎜
⎝
⎟
⎠
⎜
⎝
( ) pu
MVA
MVA
kV
kV
X 119.0
50
100
2.13
4.14
05.0
2
=⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
M2: The per‐unit initially is base on 13.8 kV and 50 MVA. Thus, the
new per‐unit values:
2
⎞⎛⎞⎛
( ) pu
MVA
MVA
kV
kV
R 219.0
50
100
2.13
8.13
1.0
2
=⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
( ) MVAkV
X 4052
1008.13
11
2
⎟⎟
⎞
⎜⎜
⎛
⎟⎟
⎞
⎜⎜
⎛
50Per Unit System |
( ) pu
MVAkV
X 405.2
502.13
1.1 =⎟⎟
⎠
⎜⎜
⎝
⎟⎟
⎠
⎜⎜
⎝
=

Example 5 (cont.)
Solution:
Per‐phase, per‐unit equivalent circuit is:
51Per Unit System |

Example 6 – Try this
A one‐line diagram of a simple power system is shown in Figure 3. The generators are
running on no‐load at their rated voltage and rated frequency with their emfs in phase.
Create per phase, per unit circuit for this power system using a base apparent power
f 100 MVA d b li lt t t G f 15 kVof 100 MVA and a base line voltage at generator G1 of 15 kV.
52Per Unit System |

Example 6 – Try this
Equipment Rating:
Synchronous Generators:
G1 : 1000 MVA 15 kV 18.021 == XX pu, 07.00 =X pu
G2 : 1000 MVA 15 kV 20.021 == XX pu, 10.00 =X pu
G3 : 500 MVA 13.2 kV 15.021 == XX pu, 05.00 =X pu, Xn =0.05 pu
G4 : 750 MVA 13 8 kV 0 30X X= = pu 100=X puG4 : 750 MVA 13.8 kV 1 2 0.30X X= = pu, 10.00 =X pu
Transformers:
T1 : 1000 MVA 15kV Δ /765 kV Y X1 = X2 = 0.1 pu dan X0 = 0.05 pu
T2 : 1000 MVA 15kV Δ /765 kV Y X1 = X2 = 0.1 pu dan X0 = 0.02 pu
T3 : 500 MVA 15kV Y/765 kV Y X1 = X2 = 0 1 pu dan X0 = 0 06 puT3 : 500 MVA 15kV Y/765 kV Y X1 = X2 = 0.1 pu dan X0 = 0.06 pu
T4 : 750 MVA 15kV Y/765 kV Y X1 = X2 = 0.1 pu dan X0 = 0.08 pu
Transmission lines:
1 – 2 765 kV X1 = X2 = 50 Ω , X0 = 150 Ω
1 3 765 kV X X 40 Ω X 100 Ω1 – 3 765 kV X1 = X2 = 40 Ω , X0 = 100 Ω
2 – 3 765 kV X1 = X2 = 40 Ω , X0 = 100 Ω
53Per Unit System |

Fundamental Power System

More Related Content

What's hot

Viewers also liked

Similar to Fundamental Power System

Recently uploaded

Fundamental Power System