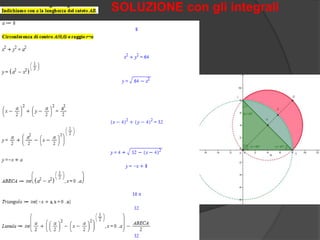
Il documento descrive la lunula di Ippocrate, una figura geometrica legata alla geometria classica, e il teorema associato che stabilisce un'equivalenza tra l'area di un triangolo rettangolo isoscele e quella della lunula stessa. Viene citato Eudemo per attestare la validità delle quadrature delle lunule eseguite da Ippocrate. La dimostrazione si basa sul calcolo delle aree mediante differenze tra superfici circolari e triangolari.

1. a cura di: Marcello Pedone
https://www.youtube.com/watch?v=d73d5wx8xxg

2. Nota storica
Si dice lunula di Ippocrate o
semplicemente LUNULA una
superficie piana delimitata da due
archi di cerchio di raggio diverso.
Prende il nome dal nome di Ippocrate
di Chio, geometra greco vissuto ad
Atene attorno al 450-420 a.C.
 Eudemo nel secondo libro della
Storia della Geometria, scrive:
"Anche le quadrature delle lunole, per
quanto sembrassero riguardar figure
non evidentemente quadrabili per la
loro affinità col cerchio, furono
eseguite da Ippocrate, e apparvero
condotte correttamente." (citazione
da: Pitagorici - Testimonianze e
frammenti, a cura di Maria Timpanaro
Cardini, La nuova Italia, Firenze, 1973,
Fasc. II, pag 43).


3. Teorema sulle Lunule di
Ippocrate (Hippocrates' lunes)
Consideriamo il triangolo
rettangolo isoscele ABC
riportato in figura: La
misura dell’area del
triangolo rettangolo
isoscele ABC è
equivalente alla misura
dell’area BECDB della
parte ROSSA indicata con
il nome di lunula (lunula di
Ippocrate).

4. DIMOSTRAZIONE
La misura della superficie della lunula BECDB, evidenziata
in rosso, può essere ottenuta come differenza di aree,
togliendo al semicerchio di centro H e raggio BH l’area
del segmento circolare BCEB pensata come l’area del
quarto di cerchio di centro A e raggio AB meno l’area del
triangolo rettangolo isoscele ABC.

5. SOLUZIONE con gli integrali