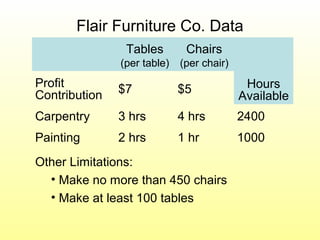
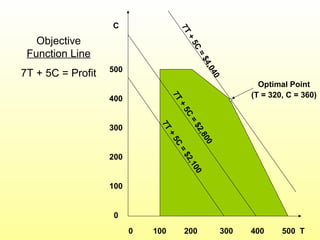
This document discusses linear programming (LP) models, including how to formulate, solve, and interpret them. Key points covered include: - The steps to develop an LP model are formulation, solution, and interpretation with sensitivity analysis. - LP models seek to maximize or minimize an objective function subject to constraints. They include alternatives and all equations are linear. - An example LP model is presented to maximize profit for a furniture company making chairs and tables given resource constraints. 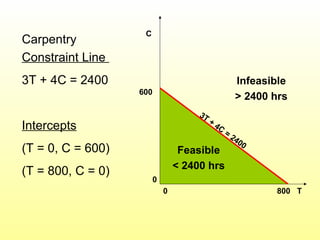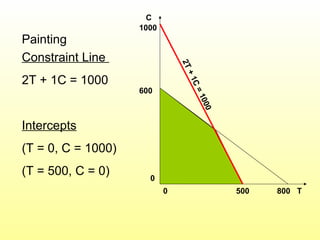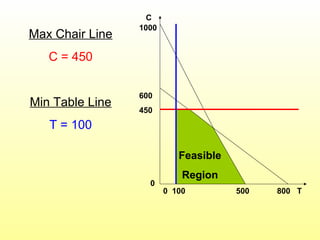- The graphical solution method is explained to provide insight into LP models and solutions. The optimal solution must occur at a corner point of the feasible region. 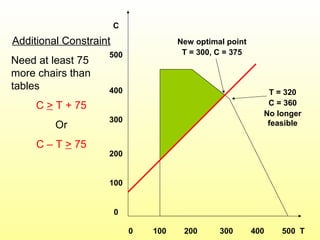- Special situations in LP like infeasibility, alternate optima, and unbounded

1. Chapter 2
Linear Programming Models:
Graphical and Computer Methods

2. Steps in Developing a Linear
Programming (LP) Model
• Formulation
• Solution
• Interpretation and Sensitivity Analysis

3. Properties of LP Models
• Seek to minimize or maximize
• Include “constraints” or limitations
• There must be alternatives available
• All equations are linear

4. Example LP Model Formulation:
The Product Mix Problem
Decision: How much to make of > 2 products?
Objective: Maximize profit
Constraints: Limited resources

5. Example: Flair Furniture Co.
Two products: Chairs and Tables
Decision: How many of each to make this
month?
Objective: Maximize profit

6. Flair Furniture Co. Data
Tables
(per table)
Chairs
(per chair)
Hours
Available
Profit
Contribution $7 $5
Carpentry 3 hrs 4 hrs 2400
Painting 2 hrs 1 hr 1000
Other Limitations:
• Make no more than 450 chairs
• Make at least 100 tables

7. Decision Variables:
T = Num. of tables to make
C = Num. of chairs to make
Objective Function: Maximize Profit
Maximize $7 T + $5 C

8. Constraints:
• Have 2400 hours of carpentry time
available
3 T + 4 C < 2400 (hours)
• Have 1000 hours of painting time available
2 T + 1 C < 1000 (hours)

9. More Constraints:
• Make no more than 450 chairs
C < 450 (num. chairs)
• Make at least 100 tables
T > 100 (num. tables)
Nonnegativity:
Cannot make a negative number of chairs or tables
T > 0
C > 0

10. Model Summary
Max 7T + 5C (profit)
Subject to the constraints:
3T + 4C < 2400 (carpentry hrs)
2T + 1C < 1000 (painting hrs)
C < 450 (max # chairs)
T > 100 (min # tables)
T, C > 0 (nonnegativity)

11. Graphical Solution
• Graphing an LP model helps provide
insight into LP models and their solutions.
• While this can only be done in two
dimensions, the same properties apply to
all LP models and solutions.

12. Carpentry
Constraint Line
3T + 4C = 2400
Intercepts
(T = 0, C = 600)
(T = 800, C = 0)
0 800 T
C
600
0
Feasible
< 2400 hrs
Infeasible
> 2400 hrs
3T
+
4C
=
2400

13. Painting
Constraint Line
2T + 1C = 1000
Intercepts
(T = 0, C = 1000)
(T = 500, C = 0)
0 500 800 T
C
1000
600
0 2T+1C=1000

14. 0 100 500 800 T
C
1000
600
450
0
Max Chair Line
C = 450
Min Table Line
T = 100
Feasible
Region

15. 0 100 200 300 400 500 T
C
500
400
300
200
100
0
Objective
Function Line
7T + 5C = Profit
7T
+
5C
=
$2,100
7T+5C
=$4,040
Optimal Point
(T = 320, C = 360)
7T
+5C
=$2,800

16. 0 100 200 300 400 500 T
C
500
400
300
200
100
0
Additional Constraint
Need at least 75
more chairs than
tables
C > T + 75
Or
C – T > 75
T = 320
C = 360
No longer
feasible
New optimal point
T = 300, C = 375

17. LP Characteristics
• Feasible Region: The set of points that
satisfies all constraints
• Corner Point Property: An optimal
solution must lie at one or more corner
points
• Optimal Solution: The corner point with
the best objective function value is optimal

18. Special Situation in LP
• Redundant Constraints - do not affect
the feasible region
Example: x < 10
x < 12
The second constraint is redundant
because it is less restrictive.

19. Special Situation in LP
• Infeasibility – when no feasible solution
exists (there is no feasible region)
Example: x < 10
x > 15

20. Special Situation in LP
• Alternate Optimal Solutions – when
there is more than one optimal solution
Max 2T + 2C
Subject to:
T + C < 10
T < 5
C < 6
T, C > 0
0 5 10 T
C
10
6
0
2T
+
2C
=
20
All points on
Red segment
are optimal

21. Special Situation in LP
• Unbounded Solutions – when nothing
prevents the solution from becoming
infinitely large
Max 2T + 2C
Subject to:
2T + 3C > 6
T, C > 0
0 1 2 3 T
C
2
1
0
Direction
of solution

22. Using Excel’s Solver for LP
Recall the Flair Furniture Example:
Max 7T + 5C (profit)
Subject to the constraints:
3T + 4C < 2400 (carpentry hrs)
2T + 1C < 1000 (painting hrs)
C < 450 (max # chairs)
T > 100 (min # tables)
T, C > 0 (nonnegativity)
Go to file 2-1.xls