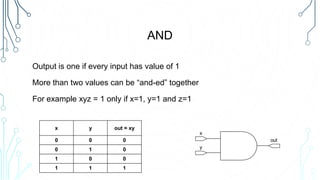
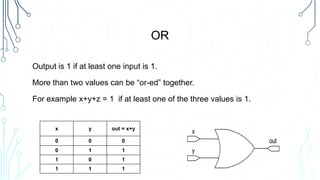
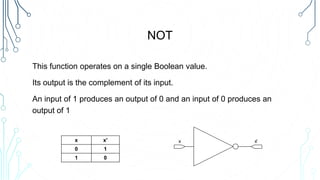
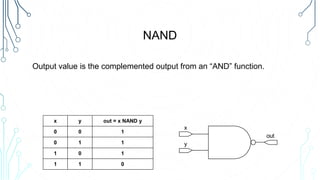
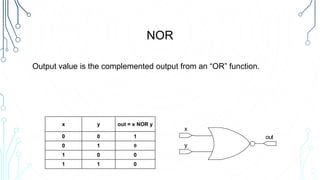
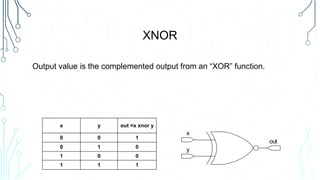
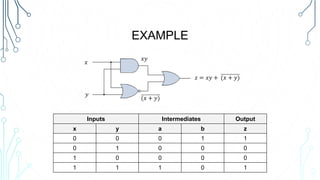
This document provides an overview of logical operations and Boolean algebra. It defines Boolean algebra values as being either true (1) or false (0). It then explains common logical operations like AND, OR, NOT, XOR, NAND and NOR and provides truth tables for each. The document also lists some basic Boolean identities and provides an example problem solving session using Boolean algebra.

1. LOGICAL OPERATIONS
& BOOLEAN ALGEBRA
ANDREI JECHIU

2. BOOLEAN ALGEBRA
Boolean algebra derives its name from the mathematician George
Boole.
A Boolean algebra value can be either true or false.
˗True is represented by the value 1.
˗False is represented by the value 0.

3. AND
Output is one if every input has value of 1
More than two values can be “and-ed” together
For example xyz = 1 only if x=1, y=1 and z=1
x y out = xy
0 0 0
0 1 0
1 0 0
1 1 1
x
y
out

4. OR
Output is 1 if at least one input is 1.
More than two values can be “or-ed” together.
For example x+y+z = 1 if at least one of the three values is 1.
x y out = x+y
0 0 0
0 1 1
1 0 1
1 1 1
x
y
out

5. NOT
This function operates on a single Boolean value.
Its output is the complement of its input.
An input of 1 produces an output of 0 and an input of 0 produces an
output of 1
x x'x x'
0 1
1 0

6. XOR (EXCLUSIVE OR)
The number of inputs that are 1 matter.
More than two values can be “xor-ed” together.
General rule: the output is equal to 1 if an odd number of input values
are 1 and 0 if an even number of input values are 1.
x y out =
0 0 0
0 1 1
1 0 1
1 1 0
yx
x
y
out

7. NAND
Output value is the complemented output from an “AND” function.
x y out = x NAND y
0 0 1
0 1 1
1 0 1
1 1 0
x
y
out

8. NOR
x y out = x NOR y
0 0 1
0 1 0
1 0 0
1 1 0
x
y
out
Output value is the complemented output from an “OR” function.

9. XNOR
Output value is the complemented output from an “XOR” function.
x
y
out
x y out =x xnor y
0 0 1
0 1 0
1 0 0
1 1 1

10. Identity name AND form OR form
Identity Law x1 = x x + 0 = x
Null (or Dominance) Law 0x = 0 1+x = 1
Idempotent Law xx = x x+x = x
Inverse Law
Commutative Law xy = yx x+y = y+x
Associative Law (xy)z = x(yz) (x+y)+z =x+(y+z)
Distributive Law x + y z = (x + y) (x + z) x(y + z) = xy+xz
Absorption Law x(x+y) = x x+xy = x
DeMorgan’s Law
Double Complement Law
BASIC BOOLEAN IDENTITIES

11. EXAMPLE
Inputs Intermediates Output
x y a b z
0 0 0 1 1
0 1 0 0 0
1 0 0 0 0
1 1 1 0 1

12. RESOURCES
• Boolean algebra
• Boolean algebra laws
• Boolean algebra #1: Basic laws and rules
• Boolean Algebra Examples