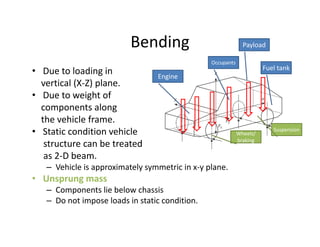
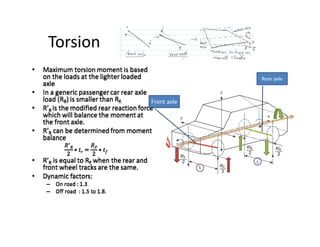
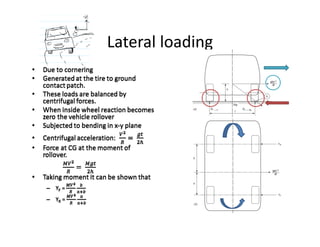
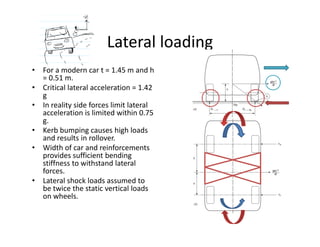
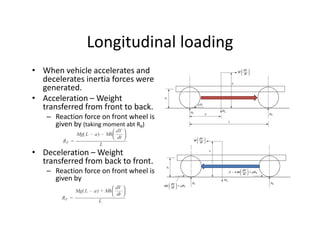
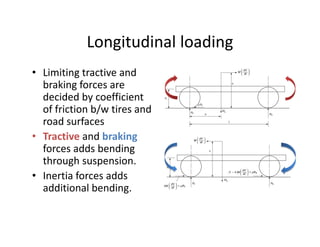
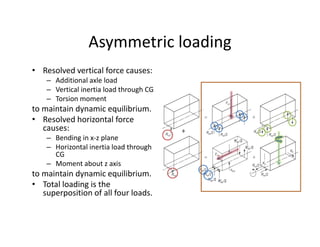
The document discusses various loading conditions and scenarios affecting vehicle dynamics, including static, dynamic, bending, and torsion loads. It outlines the effects of normal running conditions, lateral and longitudinal loading, and asymmetric loading on vehicle stability and structure. Additionally, it describes how different forces interact and balance within the vehicle under various conditions.