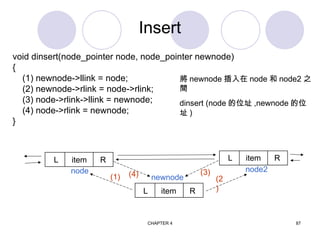
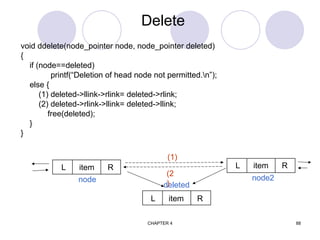
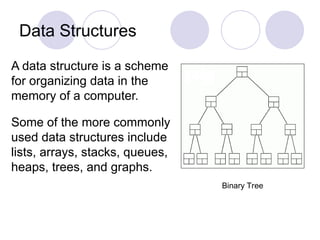
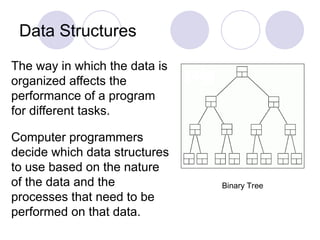
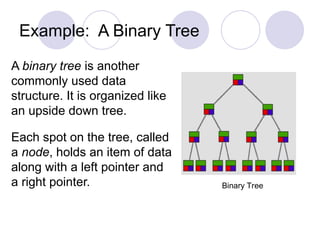
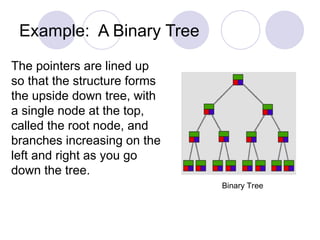
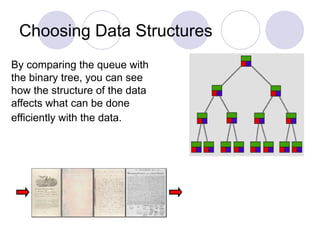
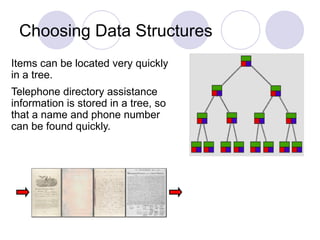
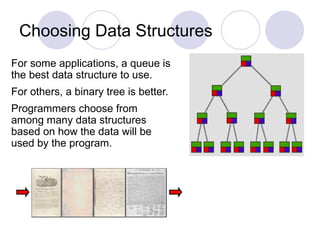
The document introduces data structures, explaining foundational concepts such as lists, arrays, stacks, queues, and binary trees, emphasizing their impact on program efficiency. It details how data structure selection depends on application needs, using examples like queues for ordered data and binary trees for efficient searching. Additionally, it discusses dynamic memory allocation for linked lists and stacks, enhancing understanding of data manipulation.


![Arrays
An array is an indexed set of variables, such as
dancer[1], dancer[2], dancer[3],… It is like a set of
boxes that hold things.
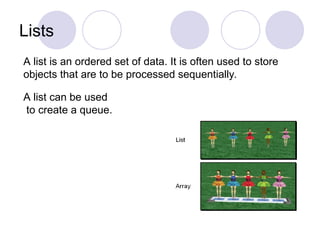
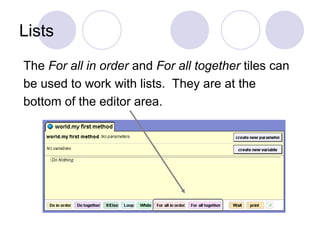
A list is a set of items.
An array is a set of
variables that each
store an item.](https://image.slidesharecdn.com/i-ii-cse-ds-unit-1-ppt-241209060930-94497858/85/Introduction-to-Data-structures-and-Trees-ppt-16-320.jpg)







![CHAPTER 4 28
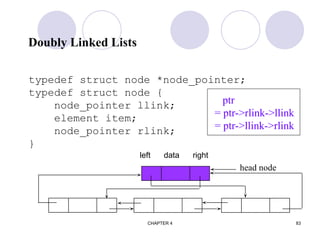
typedef struct list_node *list_pointer;
typedef struct list_node {
char data [4];
list_pointer link;
}list_node;
Creation
list_pointer ptr =NULL;
Testing
#define IS_EMPTY(ptr) (!(ptr))
Allocation
ptr=(list_pointer) malloc (sizeof(list_node));
Example 4.1: create a linked list of words
Declaration](https://image.slidesharecdn.com/i-ii-cse-ds-unit-1-ppt-241209060930-94497858/85/Introduction-to-Data-structures-and-Trees-ppt-28-320.jpg)


![CHAPTER 4 32
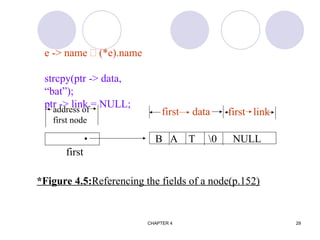
Insert GAT after FAT
(a) Insert GAT into data [5]
1 HAT
2
3 CAT
4 EAT
5 GAT
6
7 WAT
8 BAT
9 FAT
10
11 VAT
15
4
9
1
0
3
5
7](https://image.slidesharecdn.com/i-ii-cse-ds-unit-1-ppt-241209060930-94497858/85/Introduction-to-Data-structures-and-Trees-ppt-32-320.jpg)


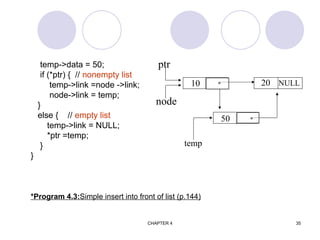
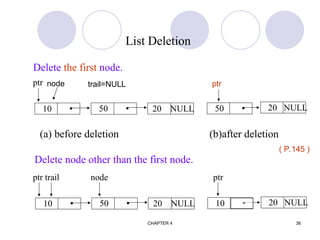


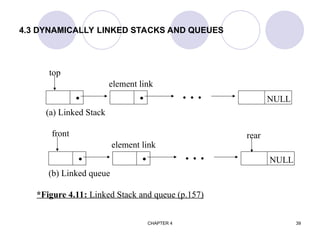
![CHAPTER 4 40
#define MAX_STACKS 10 /* maximum number of stacks */
typedef struct {
int key;
/* other fields */
} element;
typedef struct stack *stack_pointer;
typedef struct stack {
element item;
stack_pointer link;
};
stack_pointer top[MAX_STACKS];
Represent n stacks](https://image.slidesharecdn.com/i-ii-cse-ds-unit-1-ppt-241209060930-94497858/85/Introduction-to-Data-structures-and-Trees-ppt-40-320.jpg)
![CHAPTER 4 41
#define MAX_QUEUES 10 /* maximum number of queues */
typedef struct queue *queue_pointer;
typedef struct queue {
element item;
queue_pointer link;
};
queue_pointer front[MAX_QUEUE], rear[MAX_QUEUES];
Represent n queues](https://image.slidesharecdn.com/i-ii-cse-ds-unit-1-ppt-241209060930-94497858/85/Introduction-to-Data-structures-and-Trees-ppt-41-320.jpg)
![CHAPTER 4 42
void push( int I, element item)
{
/* add item to the ith stack */
stackPointer temp;
MALLOC (temp, sizeof(*temp));
temp data = item;
temp link = top[i];
top[i] = temp;
}
*Program 4.5:Add to a linked stack (p.158)
Push in the linked stack](https://image.slidesharecdn.com/i-ii-cse-ds-unit-1-ppt-241209060930-94497858/85/Introduction-to-Data-structures-and-Trees-ppt-42-320.jpg)
![CHAPTER 4 43
element pop(int i)
{/* remove top element from the ith stack */
stack_pointer temp = top[i];
element item;
if (!temp))
return
stackEmpty();
item = temp data;
top[i] = temp link;
free(temp);
return item;
}
*Program 4.6: Delete from a linked stack (p.158)
pop from the linked stack](https://image.slidesharecdn.com/i-ii-cse-ds-unit-1-ppt-241209060930-94497858/85/Introduction-to-Data-structures-and-Trees-ppt-43-320.jpg)



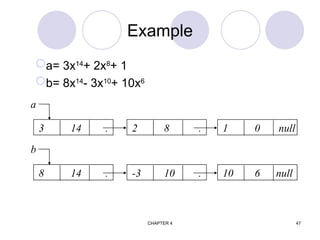
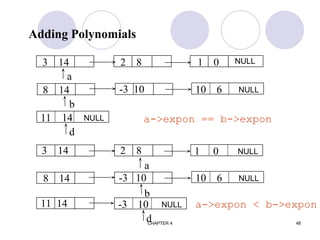
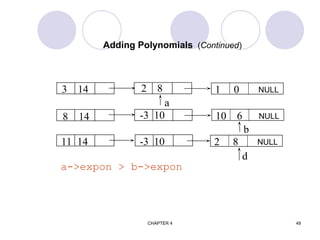






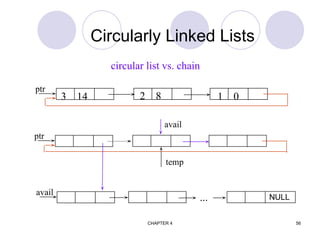


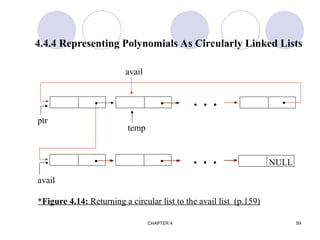
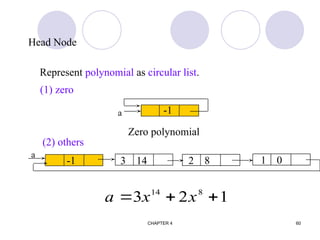



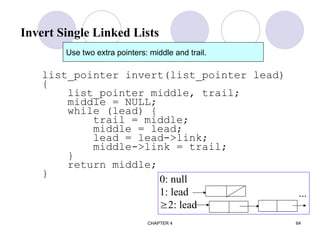

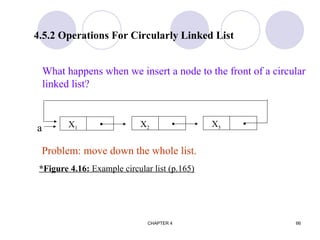
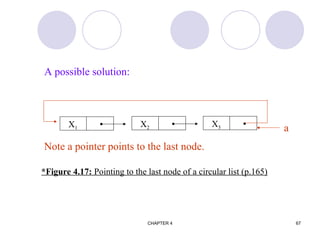
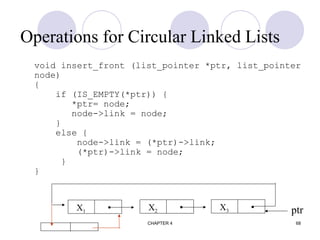


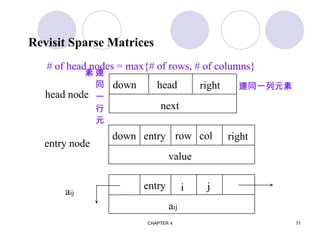
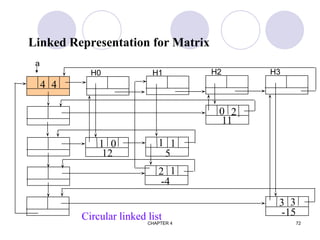

![CHAPTER 4 74
union {
matrix_pointer next;
entry_node entry;
} u;
};
matrix_pointer hdnode[MAX_SIZE];](https://image.slidesharecdn.com/i-ii-cse-ds-unit-1-ppt-241209060930-94497858/85/Introduction-to-Data-structures-and-Trees-ppt-74-320.jpg)
![CHAPTER 4 75
[0] [1] [2]
[0]
[1]
[2]
[3]
[4]
4 4 4
0 2 11
1 0 12
2 1 -4
3 3 -15
*Figure 4.22: Sample input for sparse matrix (p.174)](https://image.slidesharecdn.com/i-ii-cse-ds-unit-1-ppt-241209060930-94497858/85/Introduction-to-Data-structures-and-Trees-ppt-75-320.jpg)

![CHAPTER 4 77
scanf(“%d%d%d”, &num_rows, &num_cols,
&num_terms);
num_heads =
(num_cols>num_rows)? num_cols : num_rows;
/* set up head node for the list of head
nodes */
node = new_node(); node->tag = entry;
node->u.entry.row = num_rows;
node->u.entry.col = num_cols;
if (!num_heads) node->right = node;
else { /* initialize the head nodes */
for (i=0; i<num_heads; i++) {
term= new_node();
hdnode[i] = temp;
hdnode[i]->tag = head;
hdnode[i]->right = temp;
hdnode[i]->u.next = temp;
}
O(max(n,m))](https://image.slidesharecdn.com/i-ii-cse-ds-unit-1-ppt-241209060930-94497858/85/Introduction-to-Data-structures-and-Trees-ppt-77-320.jpg)
![CHAPTER 4 78
current_row= 0; last= hdnode[0];
for (i=0; i<num_terms; i++) {
printf(“Enter row, column and value:”);
scanf(“%d%d%d”, &row, &col, &value);
if (row>current_row) {
last->right= hdnode[current_row];
current_row= row; last=hdnode[row];
}
temp = new_node();
temp->tag=entry; temp->u.entry.row=row;
temp->u.entry.col = col;
temp->u.entry.value = value;
last->right = temp;/*link to row list */
last= temp;
/* link to column list */
hdnode[col]->u.next->down = temp;
hdnode[col]=>u.next = temp;
}
利用 next field 存放 column 的 last node](https://image.slidesharecdn.com/i-ii-cse-ds-unit-1-ppt-241209060930-94497858/85/Introduction-to-Data-structures-and-Trees-ppt-78-320.jpg)
![CHAPTER 4 79
/*close last row */
last->right = hdnode[current_row];
/* close all column lists */
for (i=0; i<num_cols; i++)
hdnode[i]->u.next->down = hdnode[i];
/* link all head nodes together */
for (i=0; i<num_heads-1; i++)
hdnode[i]->u.next = hdnode[i+1];
hdnode[num_heads-1]->u.next= node;
node->right = hdnode[0];
}
return node;
}
O(max{#_rows, #_cols}+#_terms)](https://image.slidesharecdn.com/i-ii-cse-ds-unit-1-ppt-241209060930-94497858/85/Introduction-to-Data-structures-and-Trees-ppt-79-320.jpg)