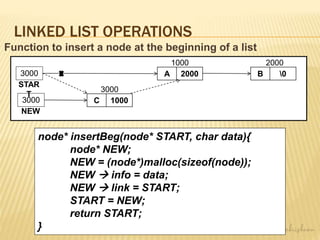
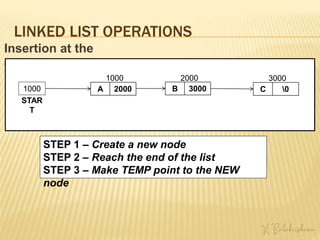
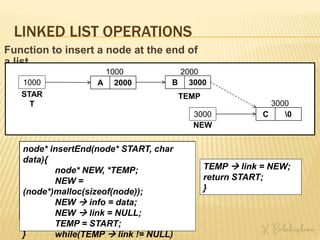
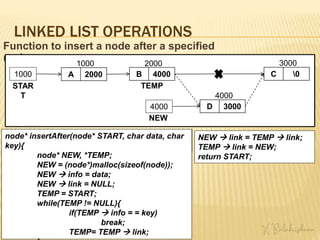
This document provides an overview of linked lists including:
- Representation of linked lists in memory using two arrays - one for node information and one for node links
- Common linked list operations like traversing, searching, insertion and deletion
- Different types of linked lists such as doubly linked lists, circular linked lists and header linked lists




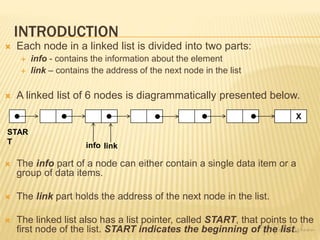
![REPRESENTATION OF LINKED LISTS IN MEMORY
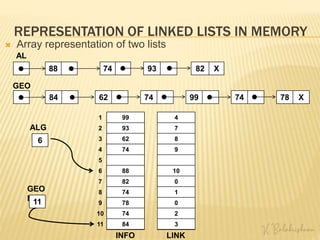
Since a simple linked list is made up of two parts(info and link), a
linked list is maintained using two linear arrays in the memory.
One array is called the INFO array and it contains the information of
all linked list nodes.
The second array is called the LINK array and it contains the
addresses of next nodes in the linked list.
The index positions in the array correspond to the list nodes.
For an index position k, INFO[k] and LINK[k] will contain the data in
node k and address of next node to k respectively.
The list also requires a variable, called START, that points to the first
node of the list.](https://image.slidesharecdn.com/module32021scheme-230108110617-df85da9e/85/Module-3-Dara-structure-notes-6-320.jpg)









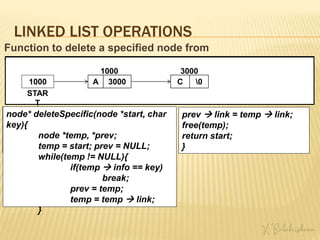
![LINKED LIST OPERATIONS
Traversing
Traversing a list involves visiting all the linked list nodes.
A 78 B 32 C 19 D 66 E 21 F 0
STAR
T
05
PTR
Algorithm: (Traversing a Linked List) This algorithm visits all nodes of a
linked list, applying an operation PROCESS on each node of the list. The
variable PTR points to the node currently being processed.
1. Set PTR := START.
2. Repeat steps 3 and 4 while PTR ≠ NULL:
3. Apply PROCESS to PTR info.
4. Set PTR := PTR link.
[End of Step 2 loop.]
5. Exit
PTR PTR
05 78 32 19 66 21
PTR PTR PTR](https://image.slidesharecdn.com/module32021scheme-230108110617-df85da9e/85/Module-3-Dara-structure-notes-19-320.jpg)
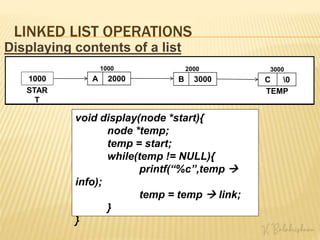
![LINKED LIST OPERATIONS
Algorithm: PRINT(START) This algorithm prints the information at each node
of the list.
1. Set PTR := START.
2. Repeat steps 3 and 4 while PTR ≠ NULL:
3. Write : PTR info.
4. Set PTR := PTR link.
[End of Step 2 loop.]
5. Exit
Algorithm: COUNT(START, NUM) This algorithm finds the number of
elements in the list.
1. Set NUM := 0.
2. Set PTR := START.
3. Repeat steps 4 and 5 while PTR ≠ NULL:
4. Set NUM := NUM + 1.
5. Set PTR := PTR link.
[End of Step 3 loop.]
5. Exit](https://image.slidesharecdn.com/module32021scheme-230108110617-df85da9e/85/Module-3-Dara-structure-notes-20-320.jpg)
![LINKED LIST OPERATIONS
Searching
Here we will see how a search for an item can be performed in an
ordered and unordered list.
Algorithm: SEARCH(START, ITEM, LOC) This algorithm finds the location
LOC of the node where ITEM first appears in an unordered linked list, or
sets LOC = NULL.
1. Set PTR := START.
2.Repeat steps 3 and 4 while PTR ≠ NULL:
3. If ITEM = PTR info, then:
Set LOC := PTR and Exit.
Else
Set PTR := PTR link.
[End of If structure.]
[End of Step 2 loop.]
4. Set LOC := NULL.
5. Exit](https://image.slidesharecdn.com/module32021scheme-230108110617-df85da9e/85/Module-3-Dara-structure-notes-21-320.jpg)
![LINKED LIST OPERATIONS
Algorithm: SEARCH(START, ITEM, LOC) This algorithm finds the location
LOC of the node where ITEM first appears in an ordered linked list, or sets
LOC = NULL. The list elements are arranged in descending order.
1. Set PTR := START.
2.Repeat step 3 while PTR ≠ NULL:
3. If ITEM < PTR info, then:
Set PTR := PTR link.
Else if ITEM = PTR info, then:
Set LOC := PTR and Exit.
Else
Set LOC := NULL, and Exit.
[End of If structure.]
[End of Step 2 loop.]
4. Set LOC := NULL.
5. Exit](https://image.slidesharecdn.com/module32021scheme-230108110617-df85da9e/85/Module-3-Dara-structure-notes-22-320.jpg)