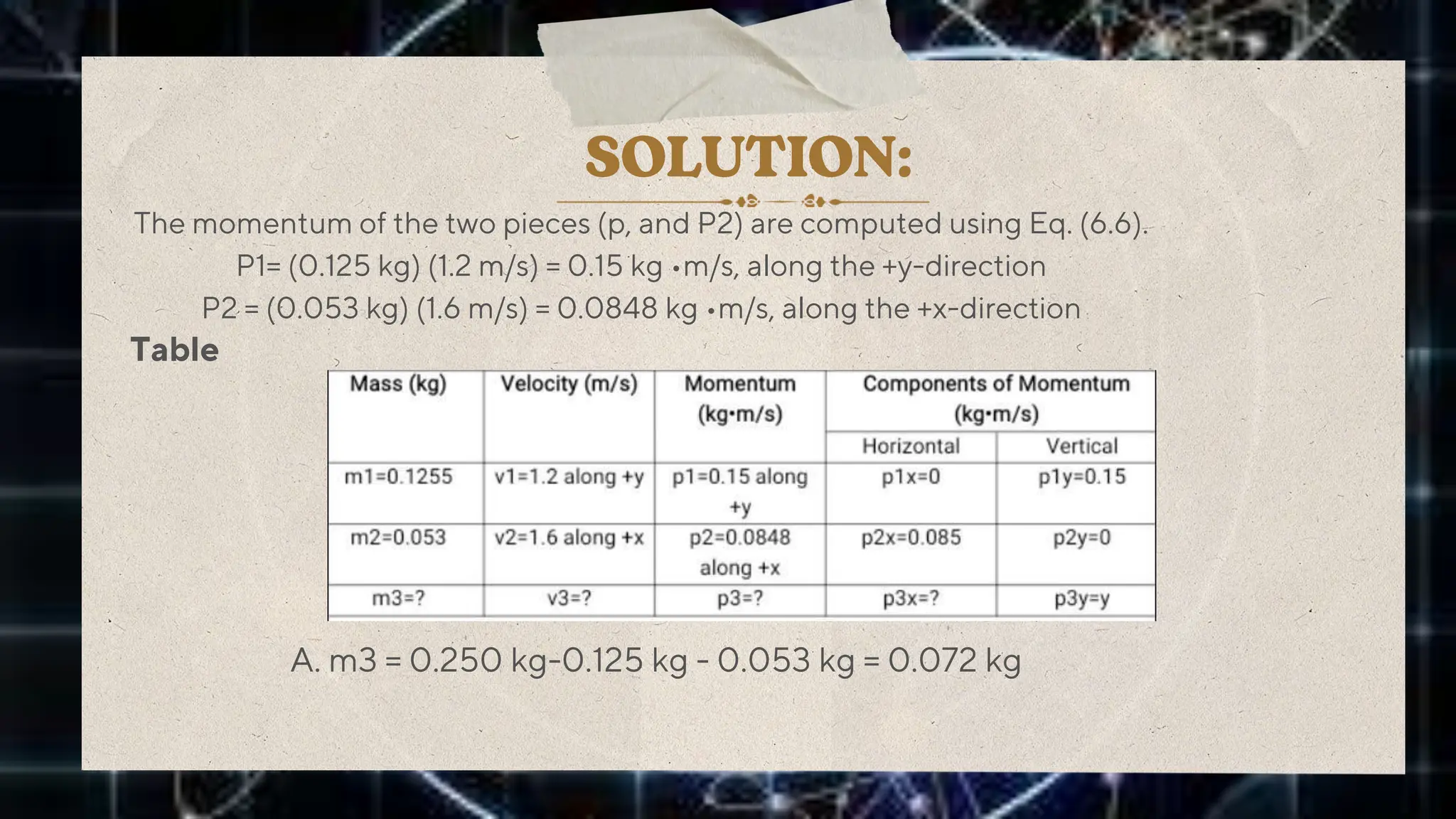
This document discusses impulse, momentum, and their relationship. It defines impulse as the product of force and time, and momentum as the product of mass and velocity. The impulse-momentum theorem states that impulse equals change in momentum. Several examples are provided to demonstrate conservation of momentum, including a person jumping off a skateboard or boat. Internal and external forces are also discussed. Worked problems demonstrate calculating momentum and using the impulse-momentum theorem to solve for unknown velocities.

2. • For this lesson,
we will know the
definition of
Impulse and
Momentum.
• In this lesson,
you can learn how
to solve regards
with impulse and
momentum.
• We will discuss
about the
conservation of
linear
momentum.

3. The impulse-momentum theorem, considered as
an alternative statement of Newton 2nd law of
motion, states that the rate of change of
momentum of a body is equal to the force applied
on it. (Formula: I=mv−mu or Ft= mv-mu )

4. • Is a vector quantity, with the same direction as the
direction of velocity.
• Momentum can be defined as "mass in motion" All
objects have mass; so if an object is moving, then it has
its mass in motion.
• Is the product of mass (m) of the object and its velocity
(v).
Momentum

5. Impulse
is defined as the product force acting on an
object and the time during which the force
acts, which means impulse is the change in
momentum. Impulse is a vector quantity
and has the same direction as the average
force.

6. • Impulse is N•s
• Momentum is kg•m/s

7. • Impulse= F∆t
• Momentum: a) p=mv-mu
b) F∆t=mv-mu

9. Hypervelocity bullets used in 0.22
long rifle usually weigh around 2.1 g
and can have a speed of 550 m/s.
What must the speed of a 75 kg man
to match the momentum of its
bullet?

10. A neophyte player catches a 125 g ball
moving at 25.0 m/s in 0.02 s. A
proffesional player catches the same ball
in 1.0 s by slightly retracting his hand
during the catch. Find the forces exerted
by the ball on the hands of the two players.

11. Conversion of Impulse Momentum: The
principle of conservation of momentum states
that if two objects collide, then the total
momentum before and after the collision will
be the same if there is no external force acting
on the colliding objects.

12. o Internal forces – the forces that the
particles of a system exert on one another.
o External forces – forces exerted on any
part of the system by other objects outside
the system.
Internal and External Forces

13. A person standing on a skateboard.
When the person pushes off the
ground in one direction, the
skateboard moves in the opposite
direction, demonstrating the
conservation of momentum.

14. A person stepping from a small boat onto a
dock. As the person moves toward the dock,
the boat moves away. Again, the total
momentum of the system (person + boat)
remains constant, but the distribution of
momentum changes, leading to the observed
motion.

15. This is also applicable in rocket propulsion.
When a rocket is fired, the expelled exhaust
gases move downward at high speed. The
downward momentum of the gases is equal
and opposite to the upward momentum of
the rocket, resulting in balanced forces.

16. This upward force exerted by the
gases is known as thrust. The
relationship between force, time, and
momentum change is described by
the impulse-momentum theorem.

18. A 50.0 kg student uses an improvised 75 kg raft in order to cross a
heavily flooded street. He noticed that as he jumps to the sidewalk
opposite the street with a speed of 1.5 m/s relative to the flood, the
raft moves away. With what the speed will the raft move relative to
flood? Assume that the raft is stationary before the student jumps to
the sidewalk. Neglect the fluid friction.

19. Consider the raft and the student as an isolated system. Let subscripts R and
S. The momentum of the system before the student jumps is equal to zero.
Formula:
0= msvs + mrvr
-mrvr=msvs
vr=-msvs/mr
Solution:
=(-50.0 kg)(1.5m/s)/ 75 kg
=-1.0 m/s
Formula
Solution
Conclusion:
Since it is negative for velocity, therefore the
raft moves backward.
Conclusion

20. A child accidentally dropped a 0.250 kg plate to the floor.
The plate broke into 3 pieces: a 0.125 kg piece moves in the
+y direction with a speed of 1.2 m/s and a 0.053 kg piece in
the +x direction at a speed of 1.6 m/s. Find (a) the mass of
the third piece and (b) the horizontal and vertical
components of its velocity.

22. The momentum of the two pieces (p, and P2) are computed using Eq. (6.6).
P1= (0.125 kg) (1.2 m/s) = 0.15 kg •m/s, along the +y-direction
P2 = (0.053 kg) (1.6 m/s) = 0.0848 kg •m/s, along the +x-direction
Table
A. m3 = 0.250 kg-0.125 kg - 0.053 kg = 0.072 kg

23. B. To determine the horizontal (v,*) and vertical (Vy) components of the velocity of the third
piece, apply the conservation of momentum for the horizontal and vertical momenta. Since
the plate has no horizontal motion as it falls on the floor, there is no horizontal momentum
before the interaction. The conservation of horizontal momentum gives
0 = 0.085 kg •m/s + P3x
P3x = - 0.085 kg • m/s.
Therefore, V3x = -0.085 kg • m/s / 0.072kg
= -1.181 m/s ~ -1.2 m/s.
The conservation of vertical momentum gives
0=0.15 kg •m/s + p3y
P3y = -0.15 kg• m/s
V3y = -0.15 kg • m/s / 0.072 kg
= -2.083 m/s ~ -2.1 m/s.A. m3 = 0.250 kg-0.125 kg - 0.053 kg = 0.072 kg