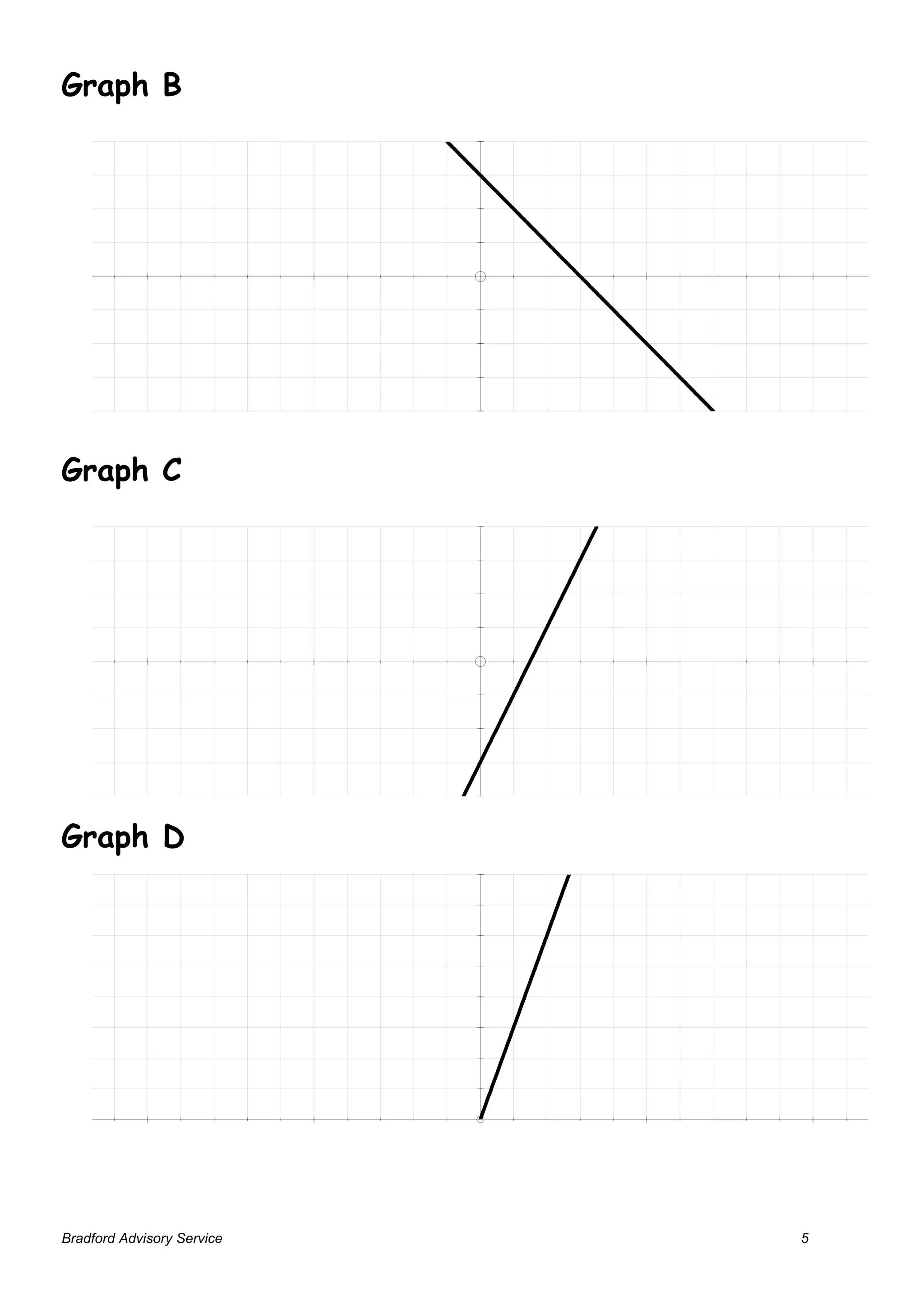
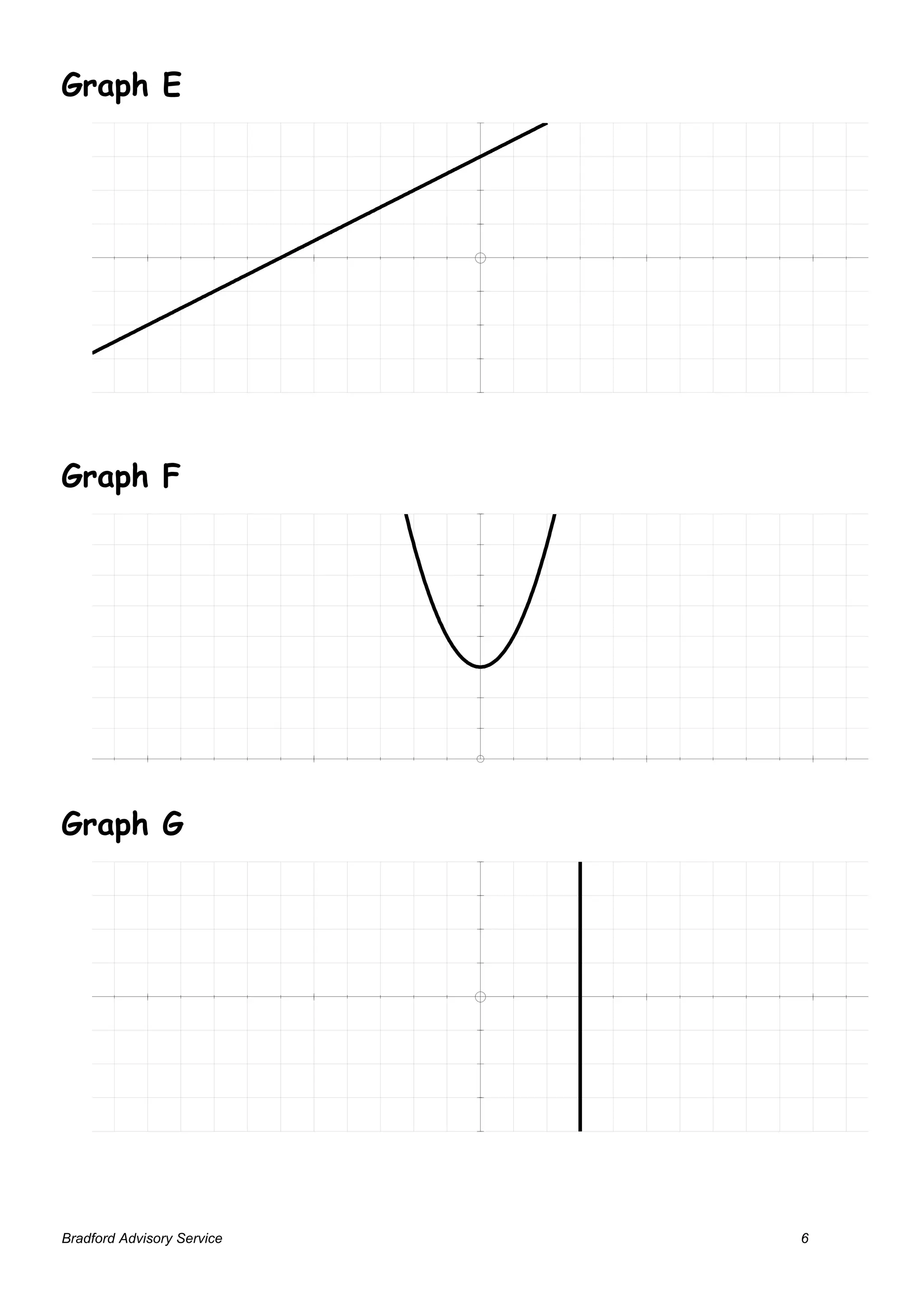
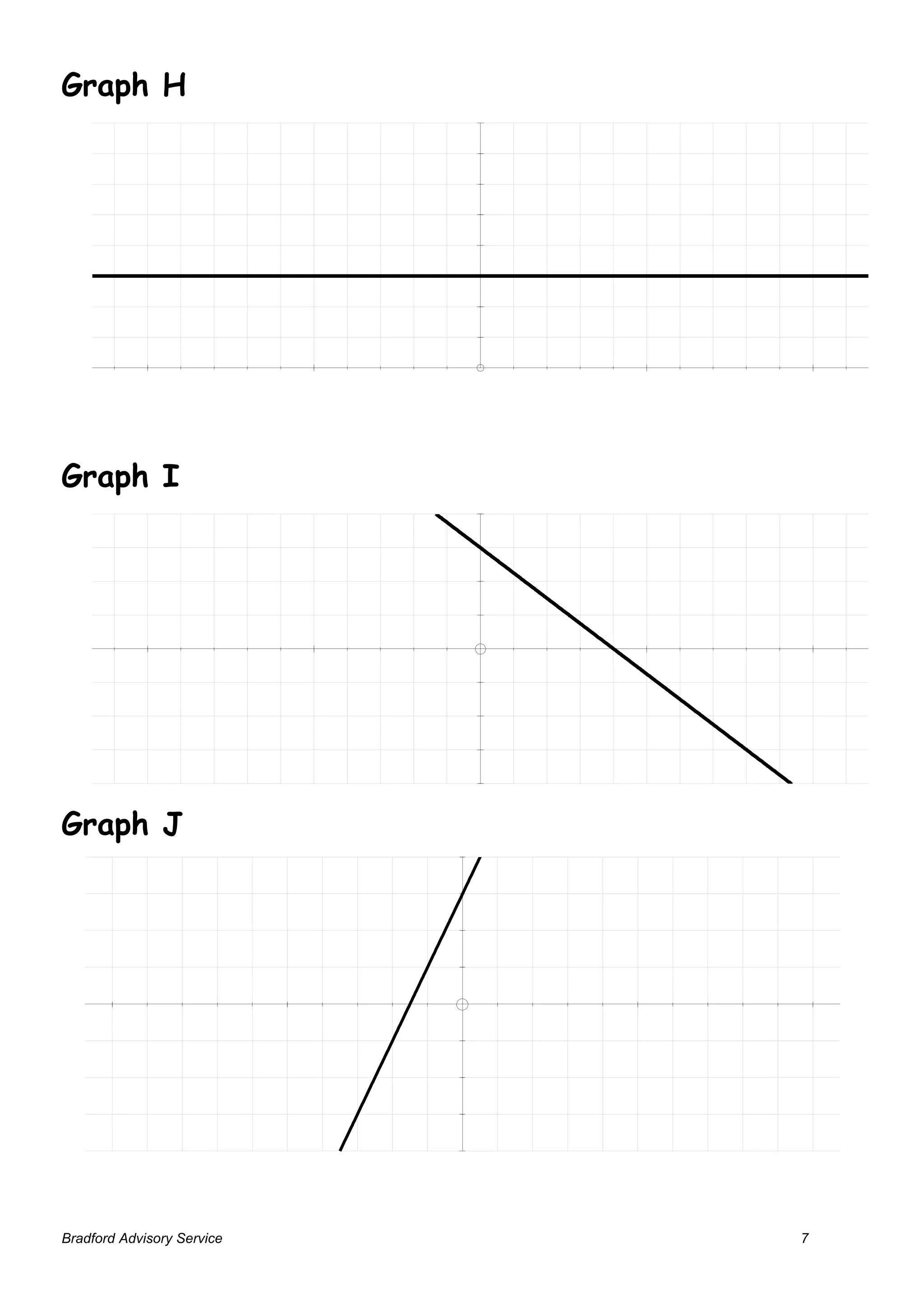
This activity involves students matching graphs of functions to their corresponding equations. Students work in groups to match equation cards to graph cards based on relationships between x and y-coordinates. They are prompted to justify their matches and discuss strategies used. The objectives were to write equations for straight lines in forms such as y=mx+c and draw graphs from equations. Variations include removing some cards or adding additional equation/graph examples.

1. Card Sort (y=mx+c, etc)
Introduction
This group activity was used in an extended plenary session at the end of
three lessons on graphing functions.
The objectives for the three lessons were:
A. To be able to write down the equation of ‘simple’ straight lines by finding
a relationship between the x and y co-ordinates.
B. To understand that all straight lines can be written in the form y=mx+c
and explain what m and c represent.
C. To be able to draw straight line graphs of the form ax+by=c
The Activity
Pupils are asked to work in groups of three or four to match the graph of the
function with its corresponding equation. Each group is expected to justify
their responses by using the table to record their answers. A list of possible
key vocabulary is included to prompt pupils. The equations have been expressed
in a form so there are no ‘obvious’ matches. Also, the number ‘3’ is included in
every equation to make the matching more difficult.
Key questions:
• What strategy did you use to match them?
• What were the clues?
• Which were easy to match? Why? Which were difficult?
In the final part of the activity, the different groups would be allocated a
graph and then asked to present their reasons for the choice they have made.
Possible Variations
• Remove two cards – one graph and one equation. The two cards should not
form a matching pair.
• Include additional cards, e.g.
- a set of co-ordinates that matches a given graph and equations,
- further examples of equations of straight lines not expressed in the
form y=mx+c and their corresponding graphs.
- include examples of quadratics of the form y=ax2+b
Bradford Advisory Service 1

2. Equations of ‘simple’ functions: Card Sort Activity
y=x+3 x+y=3 y=2x-3
The line
y=3x y=½x+3
parallel to
2 y=2x+1 and
y=x +3 x=3 passing
through the
y=3 3x+4y=12 point (0,3)
Bradford Advisory Service 2

3. Graphing Functions: Group Answer Sheet
Bradford Advisory Service 3

4. Graph of Function
Equation What strategy did you use to match Key words and
them? What were the clues? expressions
A x axis
B y axis
origin
C
gradient (m
D 4 y
3
intercept
E 2
co-ordinates
1
F y=mx+c
x
-10 -5 5 10
G -1
equation
-2
H -3 substitute
-4
I solution
linear
J
Graph A
Bradford Advisory Service 4

5. 4 y
Graph B 3
2
1
x
-10 -5 5 10
-1
-2
-3
-4
8 y
7
Graph C 6
5
4
3
2
1 x
-10 -5 5 10
Graph D
Bradford Advisory Service 5

6. 8 y
Graph E 7
6
5
4
3
2
1 x
-10 -5 5 10
4 y
3
2
Graph F
1
x
-10 -5 5 10
-1
-2
-3
-4
Graph G
Bradford Advisory Service 6

7. 4 y
Graph H 3
2
1
x
-10 -5 5 10
-1
-2
-3
-4
4 y
3
Graph I 2
1
x
-10 -5 5 10
-1
-2
-3
-4
Graph J
Bradford Advisory Service 7